宇宙大爆炸算法^[1]是一个持续的大爆炸(Big Bang)和大收缩(Big Crunch)的过程，其不要求待优化函数连续可导，也不需要待优化函数的梯度信息，算法原理和操作相对简单，易于实现，已广泛应用于函数优化^[2-3]、商业系统^[4-5]、经济调度^[6]、数据挖掘^[7]、路径规划^[8]、工业工程^[9-14]等诸多领域中.高维寻优时，BB-BC算法生成的碎片解随迭代次数的增加逐渐丧失解的多样性，同时解质量下降，陷入局部最优解的状态无法跳出，难以寻到全局最优解.因此提高搜索速度，增加碎片解的多样性和质量是提高寻优能力的根本途径.同时针对群智能优化算法的改进一直是优化研究的一个方向^[15-17].文献[14]通过引进指数分布提高碎片解多样性，提出一种指数分布大爆炸算法的改进算法，文献[17]通过混沌映射增加解的多样性，提出一种均匀大爆炸混沌大收缩(UBB-CBC)的改进算法，都在一定程度上提高了大爆炸阶段碎片解的多样性，增加了算法的寻优能力.但两个改进算法并没有解决下代碎片解质量差的问题，且算法对于跳出局部最优解的能力不强，以至于在高维寻优过程中，算法寻优能力改善并不明显.本文通过对收缩时质心的计算改进收缩速度，同时引进粒子群算法(PSO)来增加下代碎片解质量，并引进宇宙大撕裂理论增加解多样性，提高跳出局部最优解的能力，整体上提高了高维寻优时BB-BC的收敛速度.仿真实验结果表明，改进算法的优化结果要优于标准的BB-BC和UBB-CBC算法.

BB-BC算法是一个持续的爆炸和收缩过程，算法的每次收缩都会收缩于一个质心，在下次爆炸中以该质心为中心点进行爆炸，直到达到算法的结束条件时终止.以3维空间为例，爆炸过程就是以质心为球心，碎片向整个球体的空间移动的过程.

根据优化问题目标函数构造的适应度函数，在大爆炸算法运行过程中，算法会随机搜索其整个候选解空间从而找到优化问题的最优解或者次优解.BB-BC算法在初次迭代中，碎片解是在优化目标函数解空间中随机产生的，碎片解随机地分布于目标函数的整个解空间.从算法迭代的第二代起，碎片解是以算法在上代收缩过程中得到的质心为中心点，在当代解空间中爆炸产生.质心在各维空间方向上的爆炸是相互独立的，同时各个碎片解的产生过程也是相互独立的.大爆炸产生碎片解公式为

其中X_ik表示第i个碎片解第k个坐标分量；X_ck表示当代收缩质心在n维空间中第k维坐标分量；r是(－1, 1) 之间的随机数，默认服从高斯分布；a为收缩因子，在算法运行过程中为常数；t为算法运行时迭代数；x_max、x_min为目标函数解空间的上下界.

质心的产生主要有两种方式：

(1) 以每代算法中的最优解为质心.

(2) 针对当代全部碎片解的空间位置以及该碎片解的适应度值综合考虑得到质心.

第1种方式中，算法每代的收缩奇点的计算方式相对简单，只需遍历找出适应度值最优的碎片解.第2种方式中，质心的产生主要与算法每代碎片解的数量以及碎片解的适应度值有关.该种方式质心的产生主要依据式(2)：

其中，f_i是第i个碎片解的适应度值，N是当代碎片解的总数.

BB-BC算法：

Step1:初始化大爆炸大收缩算法的解集.

在问题解搜索空间内随机初始化N个碎片解.

Step2:大收缩过程.

(1) 根据适应度函数，求各碎片解的适应度值.

(2) 根据得到的各碎片解的适应度值，通过奇点收缩式(2) 得到当代质心.

Step3:大爆炸过程.

(1) 依据Step2中的质心，通过式(1) 得到下代碎片解；同时当代最优解保留进下代碎片解集.

(2) 针对得到的碎片解集进行解维度矫正.

Step4:判断结束过程.

判断是否满足停止准则，若满足则停止迭代并输出结果；否则转入Step2.

BB-BC算法在运行过程中主要存在两个问题：

(1) 收缩速度慢.由于其寻优过程中，碎片解在解空间内产生的随机性，导致上下代解之间的弱关联性，进而影响到算法的收缩速度.

(2) 难以跳出局部最优解.随迭代次数的增大，根据公式(1)，搜索空间会急速减小，进而容易陷入局部最优解中难以跳出.

粒子群算法(PSO)是一种基于群体的智能优化算法^[18-19]，群体中的每一个粒子表示目标函数问题的一个候选解，并具有与目标函数相关的适应度值.各个粒子在搜索空间中以一定速度飞行，并根据粒子自身飞行经验以及当前最优粒子状态对速度进行动态调整，个体之间通过协作与竞争，搜索问题的最优解.其实现公式为

其中V_id^t代表第t代粒子群中第i个粒子在第d维度上的速度大小；w代表惯性权重；c₁、c₂为加速常数；r₁、r₂为(0, 1) 之间的随机数；X_id^t为第t代粒子群中第i个粒子在第d维的坐标分量；P_id为当代第i个粒子在第d维经历过的最好的位置；P_gd为群体所有粒子在第d维经历过的最好位置.

由于生成的质心符合解的特性，同时质心本身特性使得其作为解的适应度值同样很小.此时，由于质心用于下一代解集的生成，其本身可以看作当代解集中的一员.根据以上分析，本文提出可以在得到质心后计算质心的适应度值，同时与当代适应度值最优的碎片解进行比较，如果质心的适应度值优于当代最优碎片解的适应度值，则选取质心替代当代最优碎片解作为奇点解进入下一代解集.

据此分析，BB-BC算法Step3更改为：

(1) 计算质心的适应度值，并与当代最优适应度值比较，如果质心的适应度值更优，则当代质心取代当代最优解作为奇点解进入下一代碎片解集.

(2) 依据Step2中的质心及公式(1) 得到下一代碎片解集.

(3) 针对得到的碎片解集进行解维度矫正.

根据公式(1), 随迭代次数的增加，BB-BC算法搜索空间逐渐减小，大大减弱碎片解的多样性，从而在算法后期容易陷入局部解的状况.

在宇宙大爆炸理论中，当宇宙扩张到一个极限值时，会出现大收缩或大撕裂两种情况.BB-BC算法使用大收缩状况.为增加解的多样性，增强算法跳出局部解的能力，本文引用大撕裂理论.在每代解中，选取适应度值最差的n_λ个解作为撕裂解，并将撕裂解中最优的解定义为逃逸解.以逃逸解作为所有撕裂解爆炸的撕裂中心，使其游离在解空间内用以随时跳出局部解.同时撕裂解不参与大收缩.撕裂解爆炸个数仍为n_λ，其中n_λ为

其中，λ为撕裂因子；N是当代碎片解的总数.同时将剩下的解作为收缩解，用以求出奇点解.

高维函数的搜索空间会随着维数的增加而大幅增加，BB-BC算法针对高维函数进行优化时需要足够多的碎片解，这样必然会导致算法的优化速度降低，从而影响优化性能，因此不仅需要增加解的多样性，还要提高其质量.将质心加入解集队列，生成奇点解，适当提高了收敛速度.在粒子群算法中粒子位置的更新受该粒子历史最优位置、粒子群中所有粒子的历史最优位置的影响.利用粒子群优化上、中、下代粒子之间的寻优联系可提高BB-BC算法在搜索空间的寻优能力和大爆炸算法的高维优化能力，改进BB-BC算法的收缩慢的问题；同时，引入宇宙大撕裂理论，在算法中加入撕裂解，增强碎片解在解空间的扩张能力，提高碎片解的多样性，从而增加算法跳出局部最优解的能力.

本文基于PSO算法、改进的奇点解方法以及大撕裂理论提出一种混合的BB-BC算法(Hybrid BB-BC，简称HBB-BC).

改进后撕裂解的爆炸公式为

改进后收缩解的爆炸公式为

其中X_ik^t为第t代解集第i个体在第k维的分量；X_wk^t为第t代解集的最劣解的第k维分量；X_ck^t为第t代解集的质心在第k维的分量；r₀、r₁、r₂为(0, 1) 之间的随机数，在产生下一代解集的大爆炸时为固定值；a为收缩因子；x_max、x_min为解集个体在单个维度上的上下界值；c₁、c₂为加速常数；每经过s代搜索空间整体减小一次，，用以放慢搜索空间的收缩速度，根据官方源码提示默认取10；P_pk为上代解集最优解在第k维的分量；P_ck为当代解集最优解(历代解集最优解)在第k维的分量.

HBB-BC算法：

Step1:初始化大爆炸大收缩算法的解集.

在问题解搜索空间内随机初始化N个碎片解.

Step2:大收缩过程.

(1) 根据适应度函数，求出碎片解的适应值；

(2) 根据式(5)，求出n_λ个撕裂解，并将剩下的碎片解作为收缩解；

(3) 根据得到的各收缩解的适应值，通过奇点收缩公式(式(2))得到当代质心.

Step3:大爆炸过程.

(1) 计算质心的适应度值，并与当代最优适应度值比较，如果质心的适应度值更优，则当代质心取代当代最优解作为奇点解进入下一代解集；

(2) 根据逃逸解和公式(式(6))，得到撕裂解爆炸的下一代碎片解集；依据Step2中的质心和公式(式(7))得到收缩解爆炸的下一代碎片解集；

(3) 针对得到的碎片解全集进行解维度矫正.

Step4:判断结束过程.

判断是否满足停止准则，若满足则停止迭代并输出结果，否则转入Step2.

对BB-BC、HBB-BC和UBB-CBC 3种算法进行实验对比.表 1和表 2为测试函数及其属性信息^[20].

表 1(Table 1)

表 1 用于实验的测试函数 Table 1 Test functions 名称 公式 F1 Shifted Sphere $ \begin{array}{l}{\mathit{F}_{\rm{1}}}{\rm{ = }}\sum\nolimits_{\mathit{i}{\rm{ = 1}}}^\mathit{n} {\mathit{z}_\mathit{i}^2} {\rm{ + f\_bias}}\\\;\;\;\;\;\;\;\;\mathit{z}{\rm{ = }}\mathit{x - o}\end{array}$ F2 Shifted Rastrigin $ \begin{array}{l}{\mathit{F}_2}{\rm{ = }}\sum\nolimits_{\mathit{i}{\rm{ = 1}}}^\mathit{n} {\left[{\mathit{z}_\mathit{i}^2-10{\rm{cos}}\left( {2\mathit{\pi }{\mathit{z}_\mathit{i}}} \right)} \right]} {\rm{ + f\_bias}}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{z}{\rm{ = }}\mathit{x - o}\end{array}$ F3 Shifted Griewank $ \begin{align} & {{\mathit{F}}_{3}}\rm{=}\left( \sum\nolimits_{\mathit{i}\rm{=1}}^{\mathit{n}}{\mathit{z}_{\mathit{i}}^{2}} \right)/\rm{4000-}\bf{\Pi }_{\mathit{i}\rm{=1}}^{\mathit{n}}\rm{cos}\left( {{\mathit{z}}_{\mathit{i}}}/\sqrt{\mathit{i}} \right){\rm{ + f\_bias}} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathit{z}\rm{=}\mathit{x-o} \\ \end{align}$ F4 Shifted Ackley $ \begin{array}{l}\;\;\;\;\;\;\;{\mathit{F}_{\rm{4}}}{\rm{ = - 20exp}}\left( { - 0.2\sqrt {\left( {\sum\nolimits_{\mathit{i}{\rm{ = 1}}}^\mathit{n} {\mathit{z}_\mathit{i}^2} } \right)/\mathit{n}} } \right) - \\{\rm{exp}}\left( {\left( {\sum\nolimits_{\mathit{i}{\rm{ = 1}}}^\mathit{n} {{\rm{cos}}\left( {2\mathit{\pi }{\mathit{z}_\mathit{i}}} \right)} } \right)/\mathit{n}} \right) + 20{\rm{ + \mathit{e} + f\_bias}}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{z}{\rm{ = }}\mathit{x - o}\end{array}$ F5 Schwefel’s Problem 2.22 $ {\mathit{F}_{\rm{5}}}{\rm{ = }}\left( {\sum\nolimits_{\mathit{i}{\rm{ = 1}}}^\mathit{n} {|{\mathit{x}_\mathit{i}}|} } \right){\rm{ + }}\left( {{\bf{\Pi }}_{\mathit{i}{\rm{ = 1}}}^\mathit{n}|{\mathit{x}_\mathit{i}}|} \right)$ F6 Schaffer $ {\mathit{F}_{\rm{6}}}{\rm{ = }}\sum\nolimits_{\mathit{i}{\rm{ = 1}}}^{\mathit{n}{\rm{ - 1}}} {{{{\rm{(}}\mathit{x}_\mathit{i}^2{\rm{ + }}\mathit{x}_{\mathit{i}{\rm{ + 1}}}^2{\rm{)}}}^{{\rm{0}}{\rm{.25}}}}} {\rm{(si}}{{\rm{n}}^{\rm{2}}}{\rm{(50}} \cdot {{\rm{(}}\mathit{x}_\mathit{i}^2{\rm{ + }}\mathit{x}_{\mathit{i}{\rm{ + 1}}}^2{\rm{)}}^{{\rm{0}}{\rm{.1}}}}{\rm{) + 1)}}$ F7 Bohachevsky $ \begin{array}{l}{\mathit{F}_7}{\rm{ = }}\sum\nolimits_{\mathit{i}{\rm{ = 1}}}^\mathit{n} {{\rm{(}}\mathit{x}_\mathit{i}^2{\rm{ + 2}}\mathit{x}_{\mathit{i}{\rm{ + 1}}}^2{\rm{ - 0}}{\rm{.3cos}}\left( {{\rm{3}}\mathit{\pi }{\mathit{x}_\mathit{i}}} \right){\rm{ - }}\mathit{p}{\rm{)}}} \\\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{P}{\rm{ = 0}}{\rm{.4cos(4}}\mathit{\pi }{\mathit{x}_{\mathit{i}{\rm{ + 1}}}}{\rm{) + 0}}{\rm{.7}}\end{array}$ F8 F7⊕F5 $ {\mathit{F}_{\rm{8}}}{\rm{ = }}{\mathit{F}_{\rm{7}}}{\rm{(part1) + }}{\mathit{F}_{\rm{5}}}{\rm{(part2)}}\mathit{n}{\rm{ = part1 + part2}}$ F9 F7⊕F5 $ {\mathit{F}_{\rm{9}}}{\rm{ = }}{\mathit{F}_{\rm{7}}}{\rm{(part1) + }}{\mathit{F}_{\rm{5}}}{\rm{(part2)}}\mathit{n}{\rm{ = part1 + part2}}$

表 1 用于实验的测试函数 Table 1 Test functions

表 2(Table 2)

表 2 测试函数的属性信息 Table 2 Attribute information of test functions 函数 参数 搜索域 F1 f_bias=0;o=－100+200*unifrnd(length(x)) [-100100] F2 f_bias=0;o=－5+10*unifrnd(length(x)) [-55] F3 f_bias=0;o=－600+1200*unifrnd(length(x)) [-600600] F4 f_bias=0;o=－32+64*unifrnd(length(x)) [-3232] F5 —— [-1010] F6 —— [-100100] F7 —— [-1515] F8 mns=0.25part1=|n·mns|part2=n－part1 [-1010] F9 mns=0.75part2=|n·mns|part1=n－part2 [-1010]

表 2 测试函数的属性信息 Table 2 Attribute information of test functions

实验中统一使用如下参数：迭代总次数为500次，解集个数m=100、维数n=30，s=10，撕裂因子λ =5，加速因子a=0.5，算法HBB-BC加速常数c₁、c₂都取1.

为更好表现算法在运行过程中的变化情况，实验采用独立20次运行取平均最优适应度值的方式进行测试，并对实验产生的每一代平均最优适应度值先经过公式(8) 处理，而后在图形上进行表示.其中$ {{\overline{{{f}^{t}}}}_{\rm{best}}}$为第t代解集的平均最优适应度值.

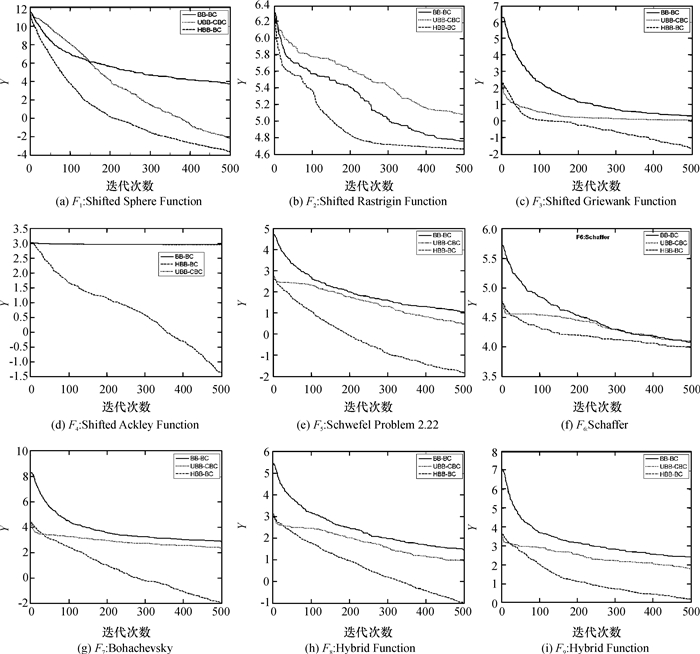
表 3为迭代结束后寻到的平均最优适应度值，图 1为20次独立迭代过程中的平均寻优变化情况.总体来说，同样的代数，HBB-BC算法能够寻到更优的解，粒子群引入和奇点解改进大幅提升算法的收敛能力，大撕裂理论的引入大大地增强算法跳出局部最优解的能力，寻优性能大幅提升，同时其收敛曲线的光滑性和鲁棒性亦不逊色于BB-BC和UBB-CBC算法.特别是F₄，BB-BC和UBB-BC全部陷入局部最优解中无法跳出，而HBB-BC算法保持着良好的寻优能力.

表 3(Table 3)

表 3 各测试函数在独立20次迭代后的平均最优适应度值 Table 3 After each test function in independent 20 iterations, the best fitness value on average 测试函数 BB-BC UBB-CBC HBB-BC F1 41.308 894 50 0.112 495 98 0.025 923 07 F2 116.988 552 00 161.754 662 00 106.462 193 00 F3 1.415 616 60 1.094 630 57 0.198 654 42 F4 19.751 991 20 19.621 253 50 0.234 737 23 F5 2.909 696 37 1.596 479 91 0.160 400 08 F6 58.711 778 20 59.928 915 60 54.064 350 20 F7 17.773 291 10 10.908 300 30 0.137 268 06 F8 4.389 904 04 2.615 187 84 0.278 293 43 F9 11.120 405 50 5.944 841 84 1.174 042 23

表 3 各测试函数在独立20次迭代后的平均最优适应度值 Table 3 After each test function in independent 20 iterations, the best fitness value on average

图 1(Figure 1)

图 1 3种算法寻优情况对比结果 Figure 1 The contrast results of three algorithms

综合表 3及图 1可以看出，本文根据BB-BC算法本身特性所提出的混合型BB-BC算法HBB-BC的优化性能明显优于原BB-BC算法和UBB-CBC算法.

本文在原BB-BC算法的基础之上，分析BB-BC算法在实际高维求解中存在的解空间搜索局限性，基于过程改进，将奇点解加入解集，并利用PSO算法对碎片解的质量进行提升.同时，利用大撕裂理论增强算法跳出局部最优解的能力，提出一种混合的BB-BC算法(HBB-BC)，并对其进行寻优性能的实验比较.根据测验结果分析，HBB-BC算法比原BB-BC算法和UBB-CBC算法的高维寻优性能更加优越，并且其收缩曲线的光滑度和算法鲁棒性同样优秀.