由于芯片及贴片元件的引脚多、间距小、焊接精度要求高等特点，以人工使用放大镜或显微镜为目检的检测方法，其检测结果的准确性、稳定性均无法满足现代自动化生产的需求^[1].自动光学检测(Automatic Optic Inspection, AOI)具有稳定可靠、高精度、高效率和非接触的优点，已成为PCB检测的重要发展方向^[2].目前常见的贴片元件的引脚焊接检测算法有模板匹配算法、统计外形建模算法^[3]、矢量图形检测算法、Particle分析算法^[4]以及基于神经网络^[5-6]等检测算法.文献[4]在提取焊点的几何特征后，通过神经网络对焊点进行分类，该方法具有较高的准确性，但是需要较多的训练样本.文献[7]提出的模板匹配法需要预先定义标准模板，受光照、噪声等因素影响较大.文献[8]通过特定结构的三色光源并建立不同类型特征矩阵模型而设计的模式匹配算法，有较高的准确性.

本文针对一款手机U盘PCB中贴片的引脚焊接情况，如图 1所示，提出一种基于图像处理的贴片引脚焊接缺陷检测算法.通过定位引脚区域的中心，经过旋转变换后提取引脚区域图像.对引脚区域进行特征提取，采用整体与局部分析的方法，先对引脚焊接情况进行初步识别，然后综合采用面积法、连通域法质心法，实现对贴片引脚处附焊球、引脚桥接、缺焊及合格情况进行自动识别.针对不同光照条件下引脚之间的焊球及焊点的面积不同的情况，本文提出基于统计方法的自适应阈值修正方法，有效解决固定阈值的局限性.

图 1(Figure 1)

图 1 手机U盘PCB正光图像 Figure 1 Positive light image of usb chip of cell phone

本文实验使用500万像素的CMOS工业相机采集U盘PCB的图像，通过USB线将图像传入电脑，图像处理软件对传入的图像进行分析、识别.通过一系列图像预处理的方法定位焊点区域的中心，经过旋转变换后提取的引脚中心区域如图 2所示.由于相机与被测物的高度和相机的焦距是固定的，因此定位焊点区域中心后提取一块200像素×80像素大小的区域，该区域只有引脚和焊点信息，如图 3所示. 2 PCB背光图像 Backlight image of PCB 3 引脚区域图像 image of pin area

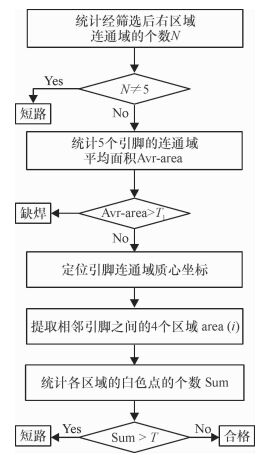
算法描述：针对这款贴片引脚曲折不直的设计方式，导致引脚二值化后连通域不连续的情况，本文提出整体与局部的方法，先对引脚区域二值化图像进行连通域筛选，再将图像分成两块，先对引脚区域右半部分(右区域)进行识别，如果检测结果有缺陷，则直接判定检测结果；如果右区域合格，则还需对整体区域识别.算法流程如图 4所示.

图 4(Figure 4)

图 4 引脚焊接缺陷识别流程图 Figure 4 Flow chart of pin welding defect identification

对提取的引脚区域图像进行灰度化之后，采用最大类间差法(OTSU)进行阈值分割^[9-10].由于噪声及助焊剂反光效应的影响，二值化之后的图像存在一些面积很小的连通域，这对引脚焊接缺陷检测造成干扰.本文通过对二值化后图像进行连通域标记，采用连通域面积筛选法过滤掉面积小于阈值T的连通域，将其相应位置的值置为0，保留面积大于阈值T的连通域，筛选后的效果如图 5所示.

图 5(Figure 5)

图 5 连通域筛选效果 Figure 5 Filtering effect of connected domain

由于这款贴片元件的引脚不是直的，在PCB平面上存在一定的高度差，因此引脚区域阈值分割后出现引脚连通域的不完整性.然而对引脚区域连通域筛选后的图像右半部分引脚连通域很完整，如图 6所示，因此本文提出先对引脚区域右半部分(右区域)进行识别.

图 6(Figure 6)

图 6 右半区域 Figure 6 The half area of the image on the right

通过第1次对连通域进行筛选之后，右区域中只剩下引脚和焊点或焊球的连通域.由于PCB中引脚区域只有5个引脚，统计右区域中连通域的个数N.当N≠5时，如果N>5，表明焊点或焊球在引脚之间且未与引脚相连；如果N＜5，表明存在焊点将两个或多个引脚相连在一起，这两种情况都可判定为引脚短路.但是当N=5时，还不能确定PCB引脚是否合格，需要对整体区域进一步判断.

当右区域连通域个数N=5时，还有可能出现缺焊情况，如图 7所示.缺焊引脚连通域面积明显比正常引脚连通域面积大很多，如图 8所示.经测试，在引脚右半区域中，缺焊的引脚连通域面积平均值为870，正常引脚平均连通域面积为510，因此可以通过引脚连通域面积来判断PCB引脚焊接是否为缺焊.统计5个连通域的面积的平均值Avr_PinArea，当Avr_PinArea>T₁时(本文设定T₁为750)，判定该PCB引脚为缺焊，反之还是不能断定为合格，还有可能是短路情况，因为引脚区域左半部分还未判断，还需要对整体区域进行判断.

图 7(Figure 7)

图 7 缺焊图像 Figure 7 Image withou welding

图 8(Figure 8)

图 8 缺焊右区域二值化 Figure 8 Binariaation of the righl area without

对右区域检测到连通域个数为5时，这5个连通域中必定是5个引脚的连通域，分别求得每个连通域质心.根据5个引脚连通域的质心坐标，计算相邻两个引脚连通域质心坐标的中点(x_i, y_i).再以y_i为基准，在二值化后的引脚区域图像中分别提取相邻两引脚之间的大小为width×20的区域，其中width为引脚区域图像的宽.提取的相邻引脚间的4个区域Area1、Area2、Area3、Area4如图 9所示.

图 9(Figure 9)

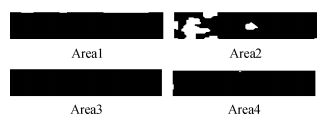
图 9 提取相邻引脚间的4个区域 Figure 9 Four extracted areas between adjacent pins

分别对提取的4个区域统计白色像素点的个数Sum，当存在有某个区域的白色点个数大于阈值T，说明相邻引脚之间存在焊点或焊球，则判定该PCB引脚焊接为短路，反之为合格.

同一个PCB测试元件，当正面光源光照强度不同时，焊点或焊球及引脚连通域的面积也不同^[9].经测试表明：在一定光照强度范围内，随着光照的增强，焊点及引脚连通域的面积会逐渐增大.由于检测环境的不确定性，焊点连通域面积筛选的阈值T也应该是自适应的^[10-13].

由于光照强度是个不可知量，阈值分割后的焊点和引脚连通域的面积都与光照强度有关，建立焊点连通域面积Z与引脚连通域面积A的关系式：Z=f(A).

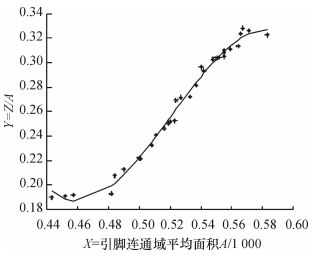
令Y =焊点连通域面积(Z)/引脚连通域面积的平均值(A)，由于A的值较大而Y的值很小，所以对A进行归一化，令X = A/1 000.对一个引脚间附有焊球的PCB板训练，通过计算焊点连通域面积A与5个引脚平均连通域面积的值，拟合出Y与X的关系曲线，如图 10所示.

图 10(Figure 10)

图 10 Y与X之间的关系曲线图 Figure 10 The relationship between Y and X

通过曲线拟合得出函数Y=-149.643 8X³+233.798X²－120.153 6X+20.530 2；近似为：Y=-150X³+234X²－120X+20.53；

由X=A/1 000，Y=Z/A，得

求出焊点连通域面积Z与引脚连通域面积平均值的关系式：

由于连通域筛选的阈值T要稍微小于真实焊点的面积，本文将式Y=Z/A改为Y = Z / (A -50)，得出阈值T的表达式：

通过计算引脚区域连通域平均值A，就可以求出对应的焊点的筛选阈值T.

本文对一个引脚短路PCB进行检测，对引脚有区域识别为合格，提取相邻引脚间4个区域分别统计其白色像素点个数，统计结果如表 1所示，检测结果为短路.

表 1(Table 1)

表 1 4个引脚间区域白色像素点分布表 Table 1 Distribution of white pixels in 4-pin area 区域 白色像素点数量/个 Area1 22 Area2 4 Area3 283 Area4 0

表 1 4个引脚间区域白色像素点分布表 Table 1 Distribution of white pixels in 4-pin area

对比文献[8]采用模板匹配法，通过计算模板水平投影直方图与引脚水平投影直方图的灰度曲线相似度方法，比较模板与引脚图像的相似度.取一个引脚短路的样品采用该算法进行测试，测试结果如表 2所示.

表 2(Table 2)

表 2 5个引脚分别与模板的相似度 Table 2 Similarity of five pins to templates respectively 引脚序号 引脚与模板的灰度曲线相似度 引脚1 0.842 5 引脚2 0.605 7 引脚3 0.635 5 引脚4 0.880 9 引脚5 0.914 9

表 2 5个引脚分别与模板的相似度 Table 2 Similarity of five pins to templates respectively

当焊点或焊球面积较小时，正常引脚与短路引脚的相似度值相差很小，难以将短路与合格引脚分离开来，同时当光照条件改变时，由于采用的固定阈值，因此检测结果误差较大^[14].

通过对400个PCB贴片引脚进行检测，其中180个为合格品，150个引脚间有焊球或短路，70个为缺焊品.检测结果如表 3所示.

表 3(Table 3)

表 3 400个样品检测结果1) Table 3 Test results of 400 sampls 焊接类型 检测结果 准确率/% 合格/个 缺焊/个 桥接/个 合格 172 1 7 95.56 缺焊 0 70 0 100 桥接 5 0 145 96.67 1) 总准确率96.75%

表 3 400个样品检测结果1) Table 3 Test results of 400 sampls

在准确率和检测时间方面，文献[5]基于神经网络方法，文献[7]基于模式匹配及其参数自适应方法，文献[8]基于相似度匹配法与本文算法对贴片引脚焊接检测情况进行了对比.在windows XP系统，CPU为主频为2.2 GHz，内存2 GB的环境下，对以上的400个PCB贴片引脚进行检测，统计检测结果如表 4所示.

表 4(Table 4)

表 4 4种算法准确率和时间数据比较 Table 4 Comparison of accuracy and time consuming of four algorithms 算法 准确率/% 时间/ms 文献[5] 98.77 47 文献[7] 96.5 55 文献[8] 95.0 26 本文算法 96.75 31

表 4 4种算法准确率和时间数据比较 Table 4 Comparison of accuracy and time consuming of four algorithms

本文研究了一款手机U盘PCB的贴片元件引脚的焊接缺陷检测算法，以引脚区域连通域面积和质心为特征，实现引脚焊接缺陷检测.建立焊点与引脚连通域面积之间的关系，给出了在不同光照条件下焊点阈值参数T的自适应校正方法.实验结果表明：该算法有较高的准确率和检测速度，可以满足工业生产的检测要求.