Search Algorithm in Cloud Computing Environment
随着信息时代的快速发展,在分布式计算、并行计算和网格计算逐步发展成熟的基础上,云计算应运而生.作为一种新兴的商业计算模型,云计算(Cloud Computing)[1]已经成为了工业界和学术界研究的热点.云计算是并行计算(Parallel Computing)[2]、网格计算(Grid Computing)和分布式计算(Distributed Computing)的发展,是虚拟化、效用计算、负载平衡等多种技术融合提升的结果.其核心思想是将大量计算资源、储存资源和服务资源等通过网络连接起来形成资源池,根据用户的需求对资源进行统一调度和管理.在云计算系统中,可按需进行动态地部署、配置、重新配置和取消服务[3].然而,由于不断增长的用户量和云计算网络中节点的异构性和复杂性,如何及时、高效地进行任务调度,合理地利用资源,提高资源利用率和任务执行的效率,成为云计算研究的核心问题之一[4].因此在云计算领域中,任务调度问题属于一个热门的课题.
1 云计算任务调度在云计算系统中,任务调度的实质是将n个相互独立的任务合理分配到m个异构的可用资源上,以达到任务调度目标[5].
云计算中资源通过虚拟化的方式提供给用户,通常云计算中任一资源VM可以被描述为
VM={vmid, mips, size, ram, bw, pesNumber}.
其中,vmid表示资源id号,mips表示CPU运行指令数,size表示资源大小,ram表示内存,bw表示带宽,pesNumber代表拥有的CPU个数.
用户提交的任一任务Clet可以被描述为
Clet={id, length, fileSize, outputSize}.
其中,id表示任务id,length代表任务长度,fileSize、outputSize分别代表任务Clet的输入、输出文件大小.
云计算的任务调度的目标[6]是对用户提交的任务实现最优调度,具体包括实现最优时间跨度(Optimal Makespan),保障服务质量(Quality of Service,QoS),保证负载均衡(Load Balancing)以及节省经济成本(Economic Principles).时间跨度是从云计算系统中第一个任务开始,直到最后一个任务执行完成过程中所消耗的时间,时间跨度越短证明调度策略越好.跨度是调度中重要且常见的目标,因此,实现最优跨度是用户和云计算提供商的共同目标.负载均衡是云计算系统中的资源分配负载平衡,达到最优化资源使用、最大化吞吐量和最小化响应时间,避免过载.
近年来,许多启发式智能算法引起了众多学者的关注和兴趣,如蚁群算法、模拟退火算法、粒子群优化算法、遗传算法等.这些算法以各自的优点对NP hard问题和组合优化问题进行求解.文献[7]提出基于改进蚁群算法的任务调度算法,有效缩短云计算环境下的任务平均运行时间.文献[8]提出基于改进遗传算法的任务调度算法,调度总任务完成时间和任务平均完成时间较短.文献[9]提出基于混合蛙跳算法的调度算法,算法保证QoS的资源调度.文献[10]提出一种融合蚁群算法和模拟退火算法的混合调度算法.该算法以最小化调度时间为目标.相对而言,布谷鸟搜索算法是一种比较新颖的群体智能启发式优化算法.国内外一些学者在此方面做了一些研究,但鲜有将此算法应用于求解云计算调度上.
本文提出了云计算系统中基于改进的布谷鸟搜索算法的调度方案,并通过仿真实验,验证了云计算系统下该算法具有良好的任务调度性能.
本文重点关注以性能为中心的最优跨度和负载均衡两个目标,并定义为
| ${\rm{Time}}\left( X \right) = \mathop {{\rm{max}}}\limits_{i = 1}^m T_i^{{\rm{VM}}},$ | (1) |
其中,Time(X)为最优跨度时间综合值;TiVM为资源i运行的总时间;m为系统中资源的数量; Time (X)值越小,代表该调度方案所用总的执行时间越短.
| $\begin{array}{l} E{\left( X \right)^{{\rm{VM}}}}{\rm{ = }}\frac{1}{m}\sum\limits_{i = 1}^m {T_i^{{\rm{VM}}}} \\ \Rightarrow D{\left( X \right)^{{\rm{VM}}}}{\rm{ = }}\frac{1}{m}{\rm{ }}{\sum\limits_{i = 1}^m {\left( {T_i^{{\rm{VM}}} - E\left( X \right)} \right)} ^2},\\ E{\left( X \right)^{{\rm{Clet}}}} = \frac{1}{n}\sum\limits_{j = 1}^n {T_j^{{\rm{Clet}}}} \\ \Rightarrow D{\left( X \right)^{{\rm{Clet}}}} = \frac{1}{n}{\sum\limits_{j = 1}^n {\left( {T_j^{{\rm{Clet}}} - E{{\left( X \right)}^{{\rm{Clet}}}}} \right)} ^2}\\ \Rightarrow {\rm{Load}}\left( X \right) = \lambda D{\left( X \right)^{{\rm{VM}}}} + \left( {1 - \lambda } \right)D{\left( X \right)^{{\rm{Clet}}}}, \end{array}$ | (2) |
其中,TCletj为任务j执行所需要的时间;n为系统中任务的数量;E(X)VM表示虚拟机运行时间的期望值;D(X)VM表示虚拟机运行时间的方差,E(X)Clet表示任务运行时间的期望值;D(X)Clet表示任务运行时间的方差;λ∈(0, 1) 为比例因子;Load(X)即本文使用的负载平衡因子;Load X值越小,代表该调度方案负载越均衡.
2 基本布谷鸟算法思想布谷鸟搜索(Cuckoo Search,简称CS)算法是一种新兴的仿生智能算法,由Xinshe Yang和S.Deb在2009年提出[11],其思想源于对布谷鸟寄生育雏行为以及鸟类或果蝇Lévy flights行为的模拟.算法由两个主要构件:Lévy flights随机游动和偏好随机游动,共同构成平衡算法的局部搜索和全局搜索的步骤.
布谷鸟搜索算法建立在3个理想条件上:
(1) 每只布谷鸟一次只产一个蛋,并且把蛋放在随机选择的鸟巢里;
(2) 孵化高质量蛋的鸟巢将会传给下一代;
(3) 可用的寄主的鸟巢数量是固定的,布谷鸟的蛋被寄主发现的概率是Pa∈[0, 1].被发现后,寄主可以把蛋扔了或者遗弃原来的鸟巢并新建一个.
在布谷鸟搜索算法中,基于莱维飞行,布谷鸟选择寄主鸟巢的位置更新式为
| $x_i^{t + 1} = x_i^t + \alpha \otimes {\rm{Lévy}}\left( {\mathit{ \lambda }} \right),$ | (3) |
其中,xit+1表示在t+1代中,第i个鸟巢的位置; xit表示在t代中,第i个鸟巢的位置; α表示步长控制量,通常用α=1; ⊗表示点乘积; Lévy(λ)服从λ(1<λ≤3) 的Lévy分布.
算法的群体由k个随机生成的布谷鸟巢组成,即群体:P={X1, X2, …Xk};每个布谷鸟巢包含n个鸟蛋,一个鸟巢代表一个候选解X={x1, x1, …, xn}.
3 基于ACCS算法的云计算任务调度 3.1 改进的布谷鸟搜索算法在云任务调度过程中,最优调度方案的求解过程是一个离散型组合优化问题,基本布谷鸟算法在进化后期容易造成早熟,易陷入局部最优解,无法搜索出全局最优解[12].由于基本布谷鸟的缺点以及云任务调度的特点,本文对基本布谷鸟算法进行如下改进,提出基于自适应柯西变异的布谷鸟搜索算法(Adaptive Cauchy Cuckoo Search,简称ACCS).
ACCS的基本思想是当布谷鸟搜索的单个鸟巢陷入局部极值时,利用柯西分布的全局变异和离散分布特点[13],对单个鸟巢进行柯西变异以增加鸟巢的多样性,有利于跳出局部极值进行全局搜索,同时提高搜索速度和质量.
当同一鸟巢在连续n代中,鸟巢的适应度平均差值仍然保持在变异范围之内,则说明此鸟巢已陷入局部最优状态,无法自主进步,需要进行外部干预.由于柯西变异在全局搜索时有较优的表现,因此本文引入柯西扰动算子,对陷入局部最优状态的鸟巢进行外部干预,进行扰动变异.
1) 柯西分布
柯西分布是一种常见的分布函数,一维柯西分布随机变量C(0, σ)的密度函数定义为
| ${f_c}\left( x \right) = \frac{\sigma }{{\left[ {{\rm{ \mathsf{ π} }}\left( {{\sigma ^{2 + }}{x^2}} \right)} \right]}}{\rm{ }}, - \infty \mathit<{x}{\rm{ }}{\rm{ }}<\infty ,$ | (4) |
其中σ为尺度参数.当σ=1时,称为标准柯西分布.
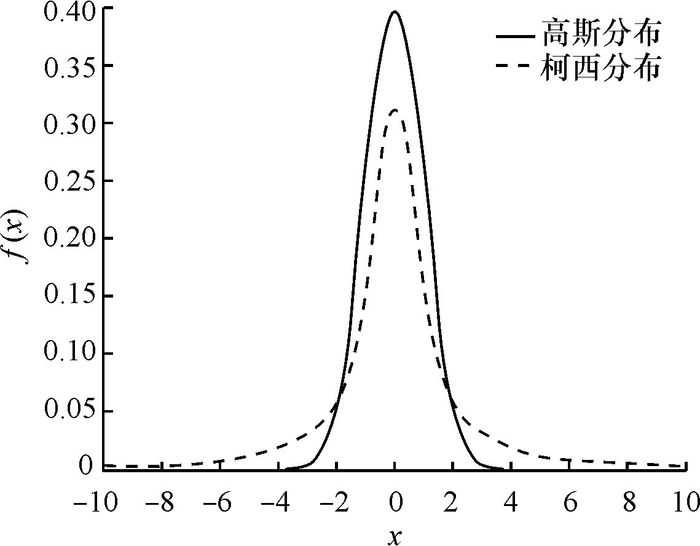
由图 1可见,柯西分布在原点的峰值比高斯分布小,而两端无限趋近于x轴的速度比高斯分布慢.说明柯西分布更易产生远离远点的随机数,柯西变异的扰动能力比高斯变异强,能有效防止算法陷入局部最优.
|
图 1 高斯随机数和柯西随机数的分布密度 Figure 1 Distribution density of Gaussian N (0, 1) random numbers and Cauchy C (0, 1) random numbers |
2) 扰动时机
| $\frac{1}{{{T_{{\rm{pre}}}}}}{\rm{ }}\sum\limits_{i = {T_{{\rm{cur}}}}}^{{T_{{\rm{cur}}}} - ({T_{{\rm{pre}}}} - 1)} {\left| {{F_i} - {F_{i - 1}}} \right| \le \delta } ,$ | (5) |
其中,Tpre表示向前比较的代数;Tcur表示当前代数;Fi表示第i代当前鸟巢的适应度值;其中Tpre<i≤Tcur;δ为扰动因子.
3) 扰动方法
| $X_{ij}^k = X_{ij}^k + C\left( {0,1} \right),$ | (6) |
其中,Xijk表示第k代鸟巢群中的第i个鸟巢的第j个蛋;C(0, 1) 表示柯西变异公式.
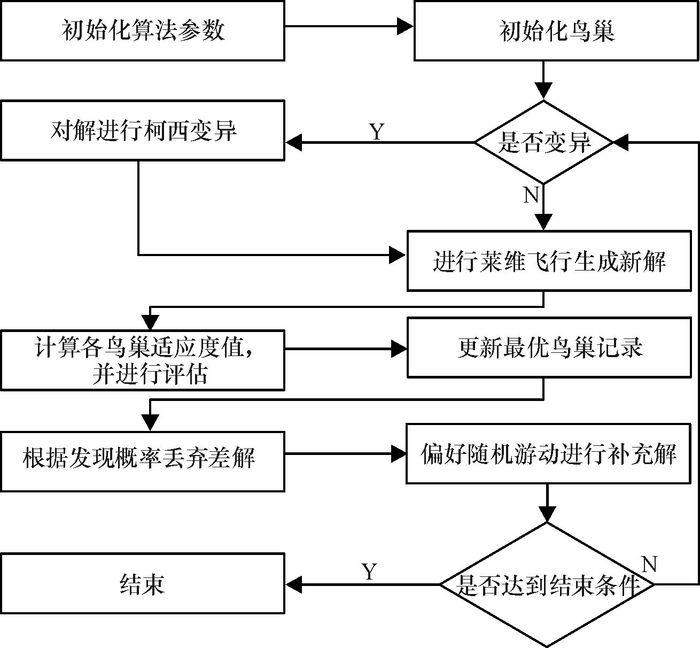
改进后的布谷鸟算法流程如图 2所示.
|
图 2 改进后的布谷鸟搜索算法流程 Figure 2 Cuckoo search algorithm for improved processes |
算法流程如下:
(1) 初始化算法基本参数;
(2) 计算各鸟巢适应度并进行评估,更新最优鸟巢记录X*;
(3) 变异判断:根据公式评估是否需进行柯西变异, 若需要,则根据式(5)~(6) 进行柯西变异,产生新的鸟巢,并评估鸟巢适应度,更新最优鸟巢记录;
(4) 莱维飞行:根据式(3) 更新鸟巢的位置,并评估新的鸟巢适应度值,对比先前最优后更新最优鸟巢记录;
(5) 产生随机数R,若R>Pa,则随机改变鸟巢位置,得到一组新的鸟巢位置;
(6) 检验算法是否满足停止条件,满足则输出最优值和对应的最优解,否则转(2) 继续下一代搜索.
3.2 ACCS的云计算资源调度设计 3.2.1 基于整数编码的调度方案资源调度方案属于组合优化问题,应用布谷鸟算法求解调度问题首先需要构造合理的编码方式来表示调度问题的解.在云任务调度中,设有n个任务需要在有m个虚拟机上执行,则代表解为n维的一元数组,每个任务对应的虚拟机号即为当前维的值.在对虚拟机号进行编码时,采用从1至m递增的整数编码.由于CS与ACCS算法迭代过程中使用的为实数编码方式,所以本文采用编码时使用式(7),解码时使用式(8) 的编解码算法调度:
| $\begin{array}{l} X = \left[ {{x_1},{x_2}, \cdots ,{x_n}} \right],\\ {x_i} \in \left[ {1,m + 1} \right),且{x_i}为实数, \end{array}$ | (7) |
| ${X^\mathit{\boldsymbol{'}}} = \left[ {\left| {{x_1}} \right|,\left| {{x_2}} \right|, \cdots ,\left| {{x_m}} \right|} \right].$ | (8) |
xi为实数,且xi∈[1, m+1), |xi |表示对xi向下取整, 解码后每一维上的数值代表对应任务所分配的执行资源序列号即虚拟机编号.
3.2.2 适应度函数设计为实现调度方案具有最优跨度和较优的负载均衡.在本文中,综合考虑调度方案的最优时间跨度时间和负载均衡,由式(1) 和(2) 可得出用来进行任务调度方案评价的目标函数式(9).其中ω∈(0, 1]为权值因子;F(X)越小,调度方案X越优:
| $F\left( X \right) = \omega \times {\rm{Time}}\left( X \right) + (1 - \omega ) \times {\rm{Load}}\left( X \right).$ | (9) |
为验证算法的有效性,本文采用了CloudSim云计算仿真器[14-15],它可对云系统上的不同调度和分配策略性能进行量化比较.为对比改进的ACCS算法与CS算法、经典遗传算法(GA)[16]和经典粒子群算法[17-18],本文同时在CloudSim上仿真模拟了GA和PSO的任务调度情况.
4.1 仿真环境与实验参数设置本文扩展了云计算仿真平台CloudSim 2.1,重写了DataCenterBroker、Cloudlet等类,对算法进行了模拟仿真.在相同的初始条件下,对基于GA算法、PSO算法、CS算法和改进的ACCS调度算法进行了基于CloudSim 2.1平台的资源调度的实验仿真.
为保持公平性,各算法基本参数均使用默认值.相关参数设置如表 1、表 2.
| 表 1 各算法的基本参数 Table 1 Basic parameters of algorithms |
| 表 2 CloudSim虚拟机(VM)配置及其他运行参数 Table 2 CloudSim virtual machine (VM) configuration and other operating parameters |
为表现算法的优越性,本文分别进行了多种任务、资源模式下的算法寻优,同时从迭代次数和寻优时间两个方面进行模拟实验.
表 3中体现了任务量逐渐增大过程中4种算法的运行情况.可以明显地看出,在经过10次500代运行过程中,4种算法在求解出的平均最优适应度值上相差不大,但ACCS算法明显优于其他3种算法.
| 表 3 50个虚拟机时各任务量(个)下各算法独立运行10次后的平均最优适应度值(F)和算法寻优平均运行时间(T)数据 Table 3 50 virtual machine quotas for the data of: the average optimal fitness after 10 times of independent operation of algorithms (F) and the average running time algorithm for optimization (T) |
在运行时间上,GA算法由于其复杂的操作,运行时间最长,是CS运行时间的近20倍,ACCS的近14倍,而且随任务量的增长,倍数呈增长趋势.同时,PSO的运行时间是CS的4~5倍,是ACCS的3~4倍.CS算法不论是在运行时间上还是寻优结果上都明显优于GA和PSO算法.而改进后的ACCS算法由于加入了扰动因子的缘故,算法的运行时间相比CS稍有增多,但寻优结果更优.即ACCS能够在相对GA和PSO更短的时间内获取到比包括CS在内的更优的解.
5 结论本文提出基于全局搜索柯西变异的布谷鸟搜索算法ACCS,并将其运用于云计算任务调度.基于最优时间跨度和负载均衡两个目标,采用整数编码方式应用ACCS算法进行求解.在CloudSim云计算仿真平台对所提算法进行仿真,同时模拟了GA、PSO算法的云计算任务调度,实验结果表明该算法能够在更短的时间内寻取到更优的调度方案,调度方案的最优时间跨度和负载均衡方面均表现良好.
| [1] | JADEJA Y,MODI K.Cloud computing-concepts,architecture and challenges[C]//IEEE.Computing,Electronics and Electrical Technologies(ICCEET). ,2012:877-880. |
| [2] |
刘东, 常静, 魏文红. 基于MPI的并行蚁群算法的研究与实现[J].
广东工业大学学报, 2008, 1(25): 38-42.
LIU D, CHANG J, WEI W H. MPI-based parallel Ant Colony algorithm and its implementation[J]. Journal of Guangdong University of Technology, 2008, 1(25): 38-42. |
| [3] |
陈康, 郑纬民. 云计算:系统实例与研究现状[J].
软件学报, 2009, 1(20): 1337-1348.
CHEN K, ZHENG W M. Cloud computing:system instances and current research[J]. Journal of Software, 2009, 1(20): 1337-1348. |
| [4] |
张建勋, 古志民, 郑超. 云计算研究进展综述[J].
计算机应用研究, 2010, 2(27): 429-433.
ZHANG J X, GU Z M, ZHENG C. Survey of research progress on cloud computing[J]. Application Research of Computers, 2010, 2(27): 429-433. |
| [5] |
林伟伟, 齐德昱. 云计算资源调度研究综述[J].
计算机科学, 2012, 10(39): 1-6.
LIN W W, QI D Y. Survey of resource scheduling in cloud computing[J]. Computer Science, 2012, 10(39): 1-6. |
| [6] |
左利云, 曹志波. 云计算中调度问题研究综述[J].
计算机应用研究, 2012, 29(11): 4023-4027.
ZUO L Y, CAO Z B. Review of scheduling research in cloud computing[J]. Application Research of Computers, 2012, 29(11): 4023-4027. DOI: 10.3969/j.issn.1001-3695.2012.11.005. |
| [7] |
王永贵, 韩瑞莲. 基于改进蚁群算法的云环境任务调度研究[J].
计算机测量与控制, 2011, 19(5): 1203-1204.
WANG Y G, HAN R L. Study on cloud computing task schedule strategy based on maco algorithm[J]. Computer Measurement & Control, 2011, 19(5): 1203-1204. |
| [8] |
李建锋, 彭舰. 云计算环境下基于改进遗传算法的任务调度算法[J].
计算机应用, 2011, 31(01): 184-186.
LI J F, PENG J. Task scheduling algorithm based on improved genetic algorithm in cloud computing environment[J]. Journal of Computer Applications, 2011, 31(01): 184-186. DOI: 10.3969/j.issn.1000-386X.2011.01.055. |
| [9] |
骆剑平, 李霞, 陈泯融. 云计算环境中基于混合蛙跳算法的资源调度[J].
计算机工程与应用, 2012, 48(29): 67-72.
LUO J P, LI X, CHEN M R. Guaranteed QoS resource scheduling scheme based on improved shuffled frog leaping algorithm in cloud environment[J]. Computer Engineering and Applications, 2012, 48(29): 67-72. DOI: 10.3778/j.issn.1002-8331.2012.29.014. |
| [10] |
张浩荣, 陈平华, 熊建斌. 基于蚁群模拟退火算法的云环境任务调度[J].
广东工业大学学报, 2014, 31(3): 77-82.
ZHANG H R, CHEN P H, XIONG J B. Task scheduling algorithm based on simulated annealing ant colony algorithm in cloud computing environment[J]. Journal of Guangdong University of Technology, 2014, 31(3): 77-82. |
| [11] | YANG X S,DEB S.Cuckoo search via Lévy flights[C].USA:IEEE Publications,2009:210-214. |
| [12] |
王李进, 尹义龙, 钟一文. 逐维改进的布谷鸟搜索算法[J].
软件学报, 2013, 24(11): 2687-2698.
WANG L J, YIN Y L, ZHONG Y W. Cuckoo search algorithm with dimension by dimension improvement[J]. Journal of Software, 2013, 24(11): 2687-2698. |
| [13] |
文诗华, 郑金华, 李密青. 多目标进化算法中变异算子的比较与研究[J].
计算机工程与应用, 2009, 45(2): 74-78.
WEN S H, ZHENG J H, LI M Q. Comparison and research of mutation operators in multi-objective evolutionary algorithms[J]. Computer Engineering and Applications, 2009, 45(2): 74-78. |
| [14] | CALHEIROS R N, RANJAN R, DE ROSE C A F, et al. Cloudsim:a novel framework for modeling and simulation of cloud computing infrastructures and services[J]. Software Practice & Experience, 2011, 41(1): 23-50. |
| [15] | CALHEIROS R N, RANJAN R, BELOGLAZOV A, et al. CloudSim: a toolkit for modeling and simulation of cloudcomputing environments and evaluation of resource provisioning algorithms[J]. Software:Practice and Experience, 2011, 41(1): 23-50. DOI: 10.1002/spe.v41.1. |
| [16] | TANG K S, MAN K F, KWONG S, et al. Genetic algorithms and their applications[J]. IEEE Signal ProcessingMagazine, 1996, 13(6): 22-37. DOI: 10.1109/79.543973. |
| [17] | EBERHART R,KENNEDY J. A new optimizer using particle swarm theory[C]. [S. l. ]:Proceedings of the Sixth International Symposium on IEEE,1995:39-43. |
| [18] | KENNEDY J,EBERHART R. Particle swarm optimization[C]. [ S. l. ]: IEEE Int Conf Neural Networks, 1995:1942-1948. |
 2016, Vol. 33
2016, Vol. 33
