2. 广东工业大学 应用数学学院,广东 广州 510520;
3. 广东省电信规划设计院有限公司 研发中心,广东 广州 510630
2. School of Applied Mathematics, Guangdong University of Technology, Guangzhou 510520, China;
3. Research and Development Center, Guangdong Planning and Designing Institute of Telecommunications Co. Ltd, Guangzhou 510630, China
LTE作为3GPP主导的第4代移动通信技术标准,其商业网络目前已经在全球范围内进行广泛部署.根据NTT DoCoMo的调查显示,运营商70%的通信业务都是发生在室内环境下,随着4G时代的到来,特别是高速数据业务的广泛应用,这一比例甚至更高.然而,在无线网络规划中,由于LTE网络的频段比2G/3G网络更高,其覆盖范围相对较小,再加上快衰落、空间链路损耗等原因,使得4G网络的室内覆盖建设很难依靠室外宏基站实现.为了提高网络质量和用户的体验需求,建设室内分布系统(简称室分系统)已成为解决网络深度覆盖的主要方式[1-3].科学的室分系统设计能有效扩大无线信号在室内的覆盖范围,提高话务容量,同时也能节约运营商的建网成本,提高经济效益,对LTE网络的发展具有非常重要的意义.
近年来,室分系统的设计呈现智能化发展,其主要思想是结合实际的工程问题建立数学模型,并设计合适的智能算法求出室分系统器件的类型和布放位置.文献[4]通过分析GSM的室内覆盖建设,建立以建网成本最低和天线口功率与实际需求方差最小为目标的数学模型,然后提出一种强制选择分枝定界算法求解该问题.但是该模型只适应2G单通道系统,对4G室分双通道模式无法适用.文献[5]以造价成本、平均峰值速率、覆盖和功率泄漏为目标函数建立了一个室分系统多目标模型,并用NSGA-Ⅱ遗传算法对模型进行求解,该算法仿真能求解出天线的数量、布放位置以及天线口的功率,对LTE室分的天线规划研究有很高的指导意义.可是,该方案所建立的模型并没有结合LTE网络的特点,所涉及的算法也无法在收敛性方面得到验证.针对系统改造问题,文献[6]在已有的2G室内分布系统基础上通过添加BBU+RRU设备改造成3G室分系统,该方案建立了一个基于0-1整数规划的TD-SCDMA室分系统数学模型,并结合该模型提出了倒推遍历算法寻找合路点和启发式算法确定最优拓扑,具有一定的借鉴意义.但由于该模型是针对TD-SCDMA建立的,与LTE室分系统的改造存在着较大差异.和现有的2G/3G室内分布系统相比较,LTE室分系统的最大特点在于引入了MIMO多天线技术.MIMO多天线技术将用户产生的数据流通过多个天线的发射和接收,建立多个收发信道,使系统的容量和小区峰值速率得到有效提升.因此,如何对传统室内分布系统进行改造,使其充分发挥MIMO技术的优势,是运营商需要重点考虑的问题.目前国内外已有一些针对MIMO双通道改造方案的研究[7-11],遗憾的是,这些研究都只是给出一些理论性的分析结果,没有涉及到实际的LTE室分系统模型.本文主要研究LTE室分系统设计中的器件组合优化问题,提出一种基于双通道改造的数学模型,并设计出符合该模型的MOEA/D-M2M算法求出一组有效解.
1 LTE室内分布系统的建设模式目前4G室内组网主要采用分布式基站的方式,即BBU+RRU+无源分布系统,在主干线上大多采用耦合器,平层则主要用功分器,如图 1所示.其中BBU和多个RRU之间用光纤连接,支持远距离传输,RRU连接无源分布系统采用多级拓扑结构,适合网络深度覆盖.根据是否实现MIMO功能,本文可以把无源分布系统的建设分为单通道模式和双通道模式.
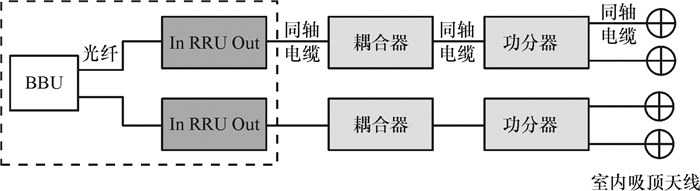
|
图 1 室内分布式基站组网 Figure 1 Indoor distributed base station networking |
单通道模式是指采用合路方式把LTE信号馈入原有的分布系统中进行传输,与现有2G/3G网络共用单路射频分布系统,如图 2所示.该模式只需在系统的前端通过合路器引入LTE信源,工程改造量小,能有效节省成本.但由于只有单个射频链路传输系统,无法利用MIMO技术提高系统容量.
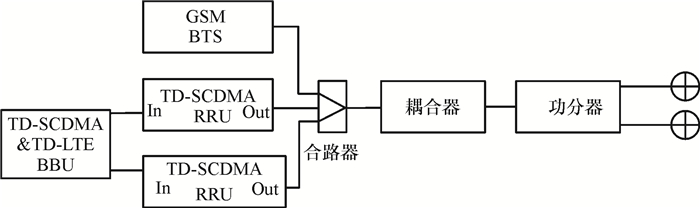
|
图 2 单通道合路模式 Figure 2 Single channel combination mode |
双通道模式是指使用两路独立的射频链路实现MIMO功能.工程上为了充分利用已有的器件,一般采用合路一路、新建一路的方式进行改造,即从RRU出来的两路LTE信号,一路通过合路器馈入到已有的单通道室内分布系统中,另一路信号使用新建的分布系统进行传输,以此形成了MIMO双流传输方式,如图 3所示.
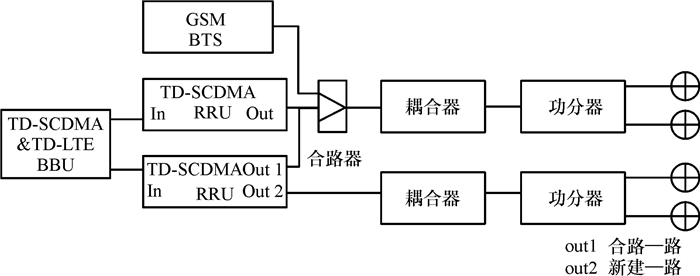
|
图 3 双通道合路模式 Figure 3 Dual-channel combination mode |
和单通道模式相比,虽然双通道模式的施工难度较大、建设成本高,但该建设模式理论上能达到两倍于单通道模式的系统最大吞吐量,在多场景多用户的实际测试中也能达到1.6倍左右的增益,充分体现MIMO技术的优势.在广覆盖的数据业务热点地区,双通道模式将是4G室内分布系统设计的首选.然而,在已有的室分改造场景中,双通道模式由于新旧两路传输系统的差异较大,很容易造成两路MIMO通道的功率不平衡.相关研究[12-13]表明,随着这种不平衡的加剧,系统的信道容量呈下降趋势.当两路信道功率相差3 dBm时,信道容量降低0.5 dBm;相差10 dBm时,信道容量下降1.7 dBm.因此在实际的工程设计中,为了实现MIMO功能,要求两条链路输出的信号能覆盖同一片区域,并且保持双链路功率差值在3 dBm之内.
2 数学模型由于室分系统中RRU级联的拓扑呈树状型分散连接到每一个对应的天线,因此本文把每个RRU连接的拓扑结构设定为一个RRU模块,其中每个RRU模块分为3级:
第一级:从RRU到主干的耦合器;
第二级:从主干的耦合器到平层的功分器;
第三级:从平层的功分器到各个天线口.
模型的已知信息有:
(1) 楼层已有的2G/3G室内分布系统拓扑结构,包括各个天线的位置和输出功率、各级馈线的长度以及功分器的类型等.
(2) 室分系统器件的相关信息,主要包括RRU的型号、价格,以及不同类型的馈线、耦合器对应的损耗及单价.
本文把模型的相关符号定义如下:
I:RRU的个数; D:RRU的种类;
Q:馈线的种类; N:耦合器的种类;
M:第i个RRU模块中耦合器的个数;
H:第i个RRU模块中天线的个数;
Pk(r):第k种RRU的单价;
Pk(f):第k种馈线的单价;
Pk(c):第k种耦合器的单价;
Lij:第i个RRU模块中第一级第j段馈线的长度;
Pij(d):第i个RRU模块中第二级第j个功分器的单价;
Lij:第i个RRU模块中第三级第j段馈线的长度;
aij:新建一路天馈系统中第i个RRU模块中第j个天线口的功率;
Uij:合路一路天馈系统中第i个RRU模块中第j个天线口的功率;
Gk:第k种RRU的发射功率;
eij:第i个RRU连接到第j个天线之间的器件总损耗;
Wk(f):第k种馈线的损耗;
Wk(c):第k种耦合器的损耗;
Wij(d):第i个RRU模块中第三级第j个功分器的损耗;
模型变量:
| $ \begin{array}{l} {r_{ik}} = \left\{ \begin{array}{l} 1, {\rm{第}}i{\rm{个RRU选择第}}k{\rm{种型号}};\\ 0, {\rm{其他}}. \end{array} \right.\\ {x_{ijk}} = \left\{ \begin{array}{l} 1, {\rm{第}}i{\rm{个RRU模块中的第一级第}}j{\rm{段}}\\ \;\;\;{\rm{馈线选择第}}k{\rm{种型号, }}j{\rm{ = 1, 2, }} \cdots M;\\ 0, {\rm{其他}}. \end{array} \right.\\ {y_{ijk}} = \left\{ \begin{array}{l} 1, {\rm{第}}i{\rm{个RRU模块中的第一级第}}j{\rm{个}}\\ \;\;\;{\rm{耦合器选择第}}k{\rm{种型号, }}j{\rm{ = 1, 2, }} \cdots M;\\ 0, {\rm{其他}}. \end{array} \right.\\ {z_{ijk}} = \left\{ \begin{array}{l} 1, {\rm{第}}i{\rm{个RRU模块中的第二级第}}j{\rm{段}}\\ \;\;\;{\rm{馈线选择第}}k{\rm{种型号, }}j{\rm{ = 1, 2, }} \cdots M + 1;\\ 0, {\rm{其他}}. \end{array} \right.\\ {s_{ijk}} = \left\{ \begin{array}{l} 1, {\rm{第}}i{\rm{个RRU模块中的第三级第}}j{\rm{段}}\\ \;\;\;{\rm{馈线选择第}}k{\rm{种型号, }}j{\rm{ = 1, 2, }} \cdots H;\\ 0, {\rm{其他}}. \end{array} \right. \end{array} $ |
模型要解决的问题是在新建的一路天馈系统中,如何选择合适的有源器件(RRU的种类)和无源器件(馈线、耦合器型号等),最终实现以最小的成本完成对室内各区域的最大覆盖.因此该数学模型的目标函数有两个:
1) 系统器件的总成本最小化
| $ \begin{array}{*{20}{l}} {{\rm{min}}\left\{ {{f_1} = \sum\limits_{i = 1}^1 {\left( {\sum\limits_{k = 1}^D {P_k^{\left( r \right)}{r_{ik}} + \sum\limits_{j = 1}^M {\sum\limits_{k = 1}^Q {{L_{ij}}P_k^{(f)}{x_{ijk}} + } } } } \right.} } \right.}\\ {\;\;\;\;\;\;\sum\limits_{j = 1}^M {\sum\limits_{k = 1}^N {P_k^{\left( c \right)}{y_{ijk}}} + } \sum\limits_{j = 1}^{M + 1} {\sum\limits_{k = 1}^Q {{{\hat L}_{ij}}P_k^{\left( f \right)}{z_{ijk}}} + \sum\limits_{j = 1}^{M + 1} {P_{ij}^{\left( d \right)} + } } }\\ {\;\;\;\;\left. {\;\;\left. {\sum\limits_{j = 1}^H {\sum\limits_{k = 1}^Q {{{\bar L}_{ij}}P_k^{\left( f \right)}{s_{ijk}}} } } \right)} \right\}.} \end{array} $ | (1) |
2) 天线口的总功率最大化
| $ {\rm{max}}\left\{ {{f_2} = \sum\limits_i^I {{a_{ij}} = \sum\limits_i^I {\left( {\sum\limits_{k = 1}^J {{G_k}{r_{ik}}-{e_{ij}}} } \right)} } } \right\}. $ | (2) |
其中,eij是一个比较特殊公式,该表达式需根据所属RRU模块中不同天线口的拓扑结构来确定.如
| $ \begin{array}{*{20}{l}} {{e_{11}} = \sum\limits_{k = 1}^Q {{L_{11}}W_k^{\left( f \right)}{x_{11k}} + \sum\limits_{k = 1}^N {W_k^{\left( c \right)}{y_{11k}} + } } }\\ {\;\;\;\;\;\;\;\sum\limits_{k = 1}^Q {{{\hat L}_{11}}W_k^{\left( f \right)}{z_{11k}} + W_{11}^{\left( d \right)} + \sum\limits_{k = 1}^Q {{{\bar L}_{11}}W_k^{\left( f \right)}{s_{11k}}} } ,}\\ \cdots \\ {{e_{14}} = \sum\limits_{k = 1}^Q {{L_{11}}{x_{11k}}W_k^{\left( f \right)} + \sum\limits_{k = 1}^Q {{L_{12}}W_k^{\left( f \right)}{x_{12k}} + } } }\\ {\;\;\;\;\;\;\;\sum\limits_{k = 1}^N {W_k^{\left( c \right)}{y_{12k}} + \sum\limits_{k = 1}^Q {{{\hat L}_{12}}W_k^{\left( f \right)}{z_{12k}}} } + W_{12}^{\left( d \right)} + }\\ {\;\;\;\;\;\;\;\sum\limits_{k = 1}^Q {{{\bar L}_{14}}W_k^{\left( f \right)}{s_{14k}}.} }\\ \cdots \end{array} $ |
约束条件
| $ \sum\limits_{k = 1}^D {{r_{ik}} = 1.} $ | (3) |
| $ \sum\limits_{k = 1}^Q {{x_{ijk}} = 1.} $ | (4) |
| $ \sum\limits_{k = 1}^N {{y_{ijk}} = 1.} $ | (5) |
| $ \sum\limits_{k = 1}^Q {{z_{ijk}} = 1.} $ | (6) |
| $ \sum\limits_{k = 1}^Q {{s_{ijk}} = 1.} $ | (7) |
| $ {a_{ij}}-{U_{ij}} < 3\;{\rm{dBm}}{\rm{.}} $ | (8) |
| $ 10\;{\rm{dBm}} < {a_{ij}} < 15\;{\rm{dBm}}. $ | (9) |
其中,式(3)~(7) 表示系统中的每一级的器件(包括RRU、耦合器和馈线)都只能选择其中一种型号.式(8) 表示新建和合路两路MIMO通道对应的天线口功率差异保持在3dBm以内,确保系统性能稳定.式(9) 根据国家对于电磁辐射防护的规定,LTE室内天线口功率控制在10~15 dBm之间.
3 算法本文建立的室内分布系统模型需要确定拓扑中各级RRU、耦合器和馈线的种类,是一个复杂的组合优化问题.该模型有多个自变量,计算复杂度随着拓扑规模的增大呈指数型增长,解空间十分巨大,寻优过程复杂.根据所建模型的特点,本文采用基于多目标遗传算法[14-16]的MOEA/D-M2M算法进行求解,MOEA/D-M2M算法的核心思想是利用分层策略把一个多目标问题分解成多个简单的子问题集合,通过相互协作的方式求解这些子问题.基于这一思想,算法首先在目标向量的空间域里设置了k个单位向量v1, v2, …, vk,形成k个子区域.然后通过计算每个个体与v1, v2, …, vk的夹角,把个体分配到与其夹角最小的单位向量所属的子区域里.在产生的每一代中,MOEA/D-M2M都保持多个子种群,其中每个子种群对应着与其相关的子问题,同时每个子种群里又包含着多个个体的解.可以看出,该算法能适当保持种群多样性,有利于寻找非支配解.
MOEA/D-M2M算法的实现步骤如下:
Step1:初始化种群,在目标空间均匀设置权重,把个体分配到各个子区域形成子种群.
Step2:设置在同一子区域里的两个个体交叉概率Pc1=0.7,在不同子区域里的两个个体交叉概率Pc2=0.3,设置变异概率Pm=0.01.通过交叉和变异,在每个子区域中产生新的个体.
Step3:运用Chebyshev选择选出下一代种群.
其中第一步采用整数编码的方式对个体进行初始化,RRU、耦合器和馈线的位置是按顺序排列的,每个符号代表着相应的位置选择哪种类型的器件.例如:假设有x个RRU,y个耦合器和z条馈线的类型需要确定,则个体编码时前x个符号表示相应位置的RRU型号,第x+1个至第x+y个符号表示对应位置的耦合器类型,余下的符号则表示相应位置的馈线类型.
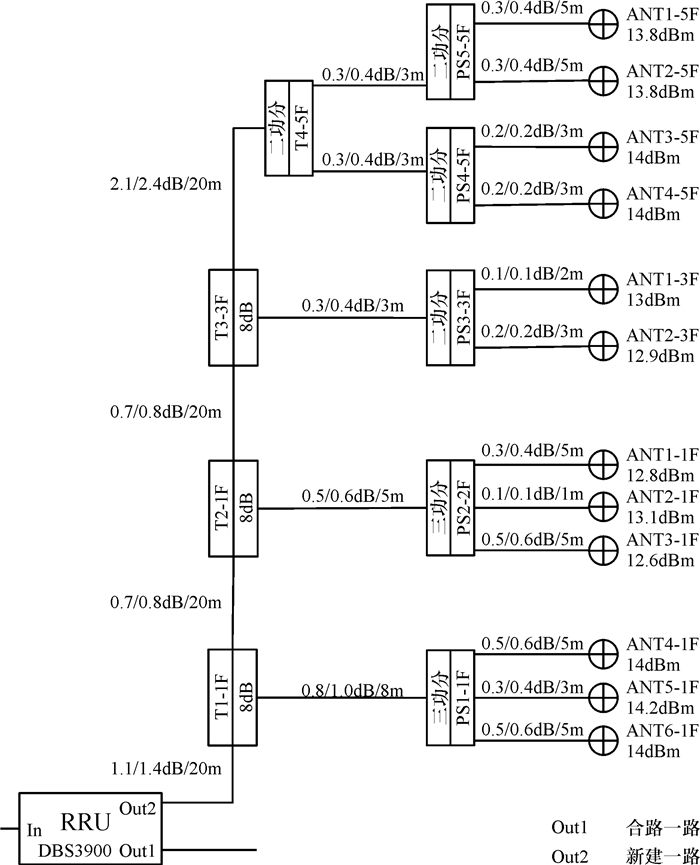
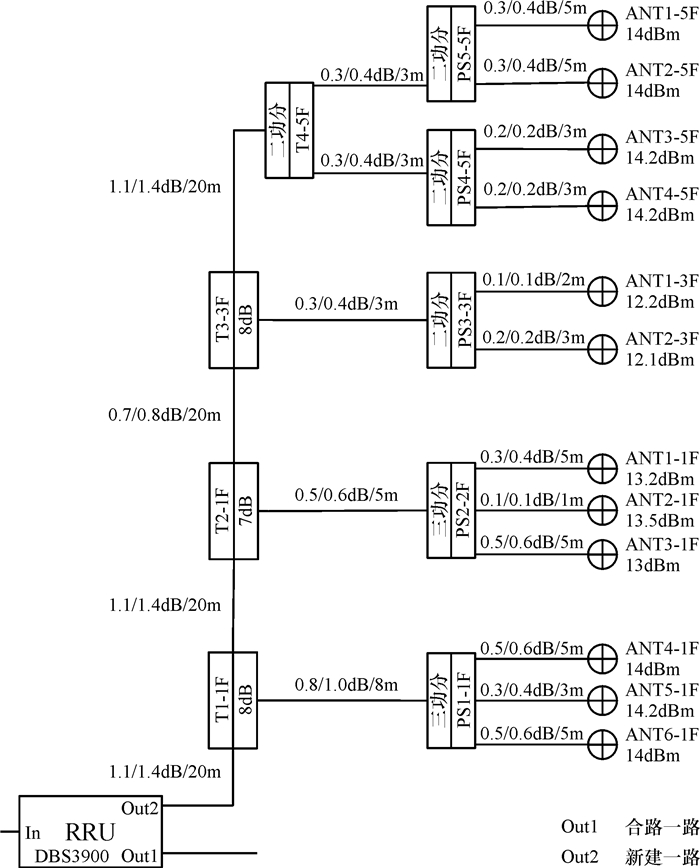
4 仿真结果根据上述MOEA/D-M2M算法的流程进行编程,本文采用Matlab7.1作为算法的仿真平台,设置该多目标进化算法的种群规模为100,进化代数为1 000,假设合路一路的各个天线口功率分别为12 dBm,12 dBm,12 dBm,12 dBm,11 dBm,11 dBm,11 dBm,11 dBm,13 dBm,13 dBm,13 dBm,13 dBm,运行程序可以计算出pareto最优解.本文选取其中的三组解集,将其应用到实际的室内分布系统设计中,可以得到该分布式系统的其中3个RRU模块的拓扑图分别如图 4~图 6所示.
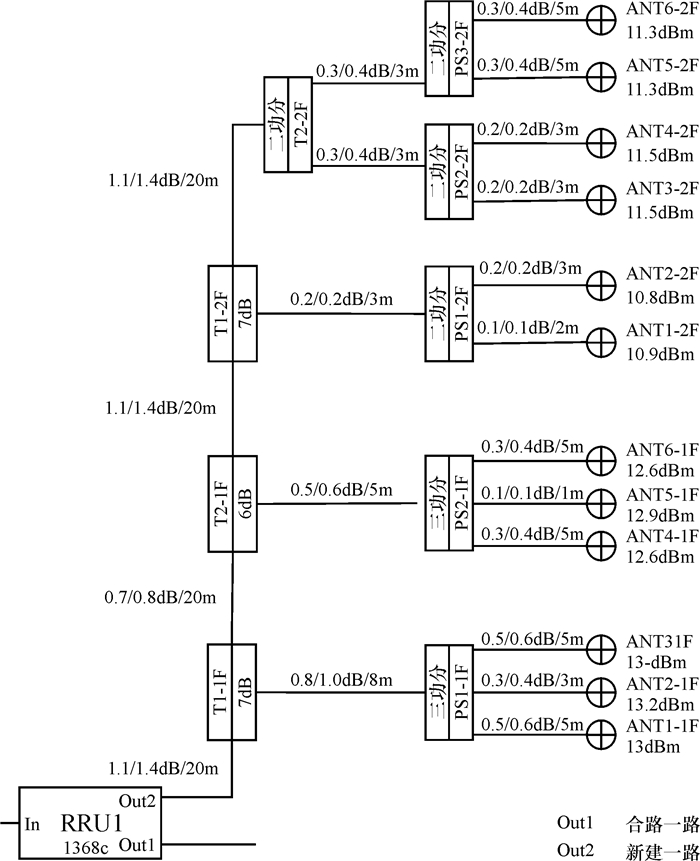
|
图 4 第一组室内分布设计图 Figure 4 The first chart of indoor distribution design |
|
图 5 第二组室内分布设计图 Figure 5 The second chart of indoor distribution design |
|
图 6 第三组室内分布设计图 Figure 6 The third chart of indoor distribution design |
仿真结果表明,本文设计的模型和算法能有效计算出室分系统中RRU、耦合器和馈线选取的型号,使得新建一路和合路一路对应的天线口的功率差值保持在3 dBm以内,各个天线的功率也维持在10~15 dBm之间,能保证系统整体的稳定性和均匀性.
5 总结本文在阐述现有LTE室内分布系统建设模式的基础上,针对双通道改造过程中遇到的MIMO双链路功率平衡问题提出一个用于系统配置优化的数学模型.该模型以系统建设成本最小化和天线口功率最大化为目标函数,并运用MOEA/D-M2M种群分解算法求出一组有效的解集.仿真结果表明本文的模型和算法能够解决该类复杂组合优化问题,为4G室内分布系统的智能化设计提供了一种思路.
| [1] |
王超. 移动通信室内分布系统设计研究[J].
邮电设计技术, 2004(2): 44-48.
WANG C. Mobile communication indoor coverage system design[J]. Designing Techniques of Posts and Telecommunications, 2004(2): 44-48. |
| [2] | VITUCCI E M, TARLAZZI L, FUSCHINI F, et al. Interleaved-MIMO DAS for indoor radio coverage: concept and performance assessment[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(6): 3299-3309. DOI: 10.1109/TAP.2014.2313136. |
| [3] |
薛楠, 文博, 吴琼. LTE室内分布系统建设方案研究[J].
邮电设计技术, 2013(1): 5-9.
XUE N, WEN B, WU Q. Research on LTE DAS construction solution[J]. Designing Techniques of Posts and Telecommunications, 2013(1): 5-9. |
| [4] |
李炯城, 易永鑫, 孙黎辉. 室内分布系统的设计和优化[J].
中国通信, 2009, 6(3A): 25-29.
LI J C, YI Y X, SUN L H. Design and optimizing of indoor distributed system[J]. China Communications, 2009, 6(3A): 25-29. |
| [5] | ATAWIA R, ASHOUR M, EI SHABRAWY T, et al. Indoor distributed antenna system planning with optimized antenna power using genetic algorithm[C]//IEEE 78th Vehicular Technology Conference. Las Vegas, NV:IEEE, 2013: 1-6. |
| [6] | 肖恒辉, 李祥鹰, 李炯城. 一类TD-SCDMA室内分布系统的设计[C]//中国通信学会通信建设工程技术委员会. 中国通信学会通信建设工程技术委员会2010年年会论文集. 厦门: 中国通信学会, 2010. 89-95. |
| [7] |
杨文博, 郭见兵. LTE MIMO室内分布系统解决方案分析[J].
电子测试, 2013(18): 141-143.
YANG W B, GUO J B. Research on indoor distribution system solutions for LTE MIMO[J]. Electronic Test, 2013(18): 141-143. |
| [8] |
田桂宾, 王懿华, 杨辉, 等. TD-LTE室内分布系统双通道改造替代方案的研究[J].
电信工程技术与标准化, 2012, 25(3): 48-52.
TIAN G B, WANG Y H, YANG H, et al. Research on indoor distributed system dual channel reforming alternative scheme for TD-LTE[J]. Telecom Engineering Technics and Standardization, 2012, 25(3): 48-52. |
| [9] |
程日涛, 汪颖, 汤利民. 利用TD-LTE变频系统在单路分布系统中实现MIMO传输[J].
移动通信, 2012(22): 42-47.
CHENG R T, WANG Y, TANG L M. Achieving MIMO transmission by TD-LTE frequency conversion system in single changnel distributed system[J]. Mobile Communications, 2012(22): 42-47. DOI: 10.3969/j.issn.1006-1010.2012.22.010. |
| [10] | 曾唯彬. TD-LTE双流分布系统覆盖优化研究[D]. 广州: 华南理工大学电子与信息学院, 2013. |
| [11] | 龚熙. 基于TD-LTE室内分布系统改造的有源天线的研究与设计[D]. 武汉邮电科学研究院, 2014. |
| [12] | 高泽华, 高峰, 林海涛, 等. 室内分布系统规划与设计—GSM/TD-SCDMA/TD-LTE/WLAN[M]. 北京: 人民邮电出版社, 2013: 169-171. |
| [13] |
王森, 张必达, 席向涛. 基于FDD-LTE的室内覆盖解决方案探讨[J].
邮电设计技术, 2013, 10: 35-38.
WANG S, ZHANG B D, XI X T. Discussion on the solution of indoor distribution antenna system based on FDD-LTE[J]. Designing Techniques of Posts and Telecommunications, 2013, 10: 35-38. DOI: 10.3969/j.issn.1007-3043.2013.04.009. |
| [14] |
刘海林, 刘永清. 多目标最优化进化算法中适应性的选择[J].
广东工业大学学报, 2002, 19(1): 7-10.
LIU H L, LIU Y Q. The fitness selection about evolutionary algorithms for multiobjective optimization[J]. Journal of Guangdong University of Technology, 2002, 19(1): 7-10. |
| [15] | LIU H L, GU F Q, CHEUNG Y M. T-MOEA/D: MOEA/D with Objective Transform in Multi-objective Problems[C]//Information Science and Management Engineering (ISME) 2010 conference. Shanxi: IEEE, 2010:282-285. |
| [16] | LIU H L, GU F Q, ZHANG Q F. Decomposition of a multiobjective optimization problem into a number of simple multiobjective subproblems[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(3): 450-455. DOI: 10.1109/TEVC.2013.2281533. |
 2016, Vol. 33
2016, Vol. 33