2. 广东省物联网与控制专用芯片及系统智能化工程技术研究中心, 广东工业大学 广东 广州 510006
2. Guangdong Provincial Research Center of Internet of Things, Control Special Chip and Intelligent System Engineering Technology, Guangdong University of Technology, Guangzhou 510006, China
无线传感器网络是一种全新的信息获取和处理技术,并以其低成本、低功耗、分布式和自组织等特点得到广泛应用.基于位置定位的服务(LBS)在现实生活中也越来越受到关注,人们对定位与导航的需求日益增大.虽然目前通用的GPS定位已经应用在很多领域中,但是GPS在特殊的环境中信号会中断,无法在室内环境中取得较高的精度,因此不适用于室内机器人的定位.相反,新兴的一些基于无线信号的室内定位技术相应出现,如无线局域网(WiFi)[1]、射频标签(RFID)[2]、超宽带无线电(UWB)[3]、紫蜂(ZigBee)[4]、蓝牙(Bluetooth)[5]等技术.从技术成熟与应用规模角度考虑,Wi-Fi定位无疑是当前最主流,也是未来最具发展潜力的室内定位技术.
目前所使用的室内无线信号定位算法大概分为两类:基于测距(range-based)和无需测距(range-free).前者通过测量节点间点到点的距离或者角度信息得到估计位置,常用的测距技术有接收信号强度(Received Signal Strength Indicator, RSSI)、TOA、TDOA[6]和AOA[7]等;后者根据网络的连通性等信息来估计节点的位置,典型的非测距模型有K最近邻法、DV-HOP法和质心法.RSSI信号易受环境(反射,多径传播)的影响,所以将RSSI值转化成距离的时候必然存在误差.比较而言,虽然RSSI测距误差比较大,但是节点有较好的硬件机制支持,并可以结合高斯模型[1]等一些滤波函数来提高其精度,且由电磁波信号衰减理论可知,同一方向的RSSI值是唯一的,因此可以作为定位环境中的位置指纹.由[8]可知,当采用三边测量定位算法的时候可能造成3个圆没有相交点的情况,使所得的非线性方程组无解,而文献[9]中位置指纹算法可以有效地解决这样的问题.
位置指纹算法包括两个阶段:离线采样与在线定位.离线采样阶段的主要生成包含有样本节点RSSI值的样本指纹库.传统方法是首先在空间中设置一系列样本点和若干个无线接入点AP(Access Point),通过多次测量收集样本点的RSSI值从而形成样本点的位置指纹库.在线定位阶段主要根据盲节点的RSSI值采用某种搜索匹配算法与位置指纹库中的数据进行匹配,传统的匹配算法如K最近邻法,文献[10]将模糊三角形定位的思想引入到基于RSSI室内定位中,在一定程度上提高了定位的精度.
传统构建位置指纹库的算法很简单,提前选择好室内测量的样本点,然后测量样本点与AP的RSSI值,存入数据库,这种方法虽然比较稳定,但是耗费比较大的人力和物力,并且如果一旦定位环境转移,样本节点的选择也要发生变化,那么数据库必须重新构建.在实际的定位过程中,当测量出一小部分样本点的RSSI值时,这些RSSI值不仅可以提供当前样本点的信息,而且也体现了这些样本点与周围环境的某种联系.因此利用样本点之间空间相关性,通过较少样本点的测量就可以建立一个比较密集的位置指纹数据库.文献[11]中提出利用地理学上的克里格插值算法和距离加权倒数空间插值法来构建位置指纹库,这两种算法虽然能够降低构建误差,但考虑需要耗费较多的计算时间,因此在实际环境中普及度不高.统计学上常用的插值法有牛顿插值、拉格朗日插值、分段插值、样条插值、Hermirtc插值[12].其中拉格朗日插值模型简单,结构紧凑,且重心拉格朗日插值算法插值计算更加简便,插值效果稳定.较之于其他插值算法比较适用于快速建立位置指纹库.
室内定位点的稀疏性使得压缩传感理论[13]同样能应用于构建位置指纹库.压缩传感理论主要包括信号的稀疏表示、编码测量和重构算法3个方面.信号的稀疏表示就是将信号投影到正交变换基时, 绝大部分变换系数的绝对值很小, 所得到的变换向量是稀疏或者近似稀疏的, 可以将其看作原始信号的一种简洁表达, 信号重构过程一般转换为一个最小l0范数的优化问题, 然后通过原始信号与测量矩阵的乘积获得原始信号的线性投影测量.最后, 运用重构算法由测量值及投影矩阵重构原始信号.信号重构过程一般有最小l1范数法[14]、匹配追踪系列算法[14]、最小全变分方法[15]、迭代阈值算法[16]等.
1 采用压缩传感构建位置指纹库如果室内的AP数量为m,定位空间内n个样本点对应的RSSI向量均可以被测定,n个样本点的向量表达式R为:
| $ \mathit{\boldsymbol{R}} = \left[\begin{array}{l} {\mathit{\boldsymbol{R}}_1}\\ \; \vdots \\ {\mathit{\boldsymbol{R}}_i}\\ \; \vdots \\ {\mathit{\boldsymbol{R}}_n} \end{array} \right] = \left[\begin{array}{l} {r_{11}}\;{r_{12}}\; \cdots \;{r_{1m}}\\ \; \vdots \;\;\;\; \vdots \;\;\;\;\; \vdots \;\;\;\;\; \vdots \\ {r_{i1}}\;{r_{i2}}\;\; \cdots \;{r_{im}}\\ \; \vdots \;\;\;\; \vdots \;\;\;\;\; \vdots \;\;\;\;\; \vdots \\ {r_{n1}}\;{r_{n2}}\; \cdots \;{r_{nm}} \end{array} \right]. $ | (1) |
其中ri来表示i从k(k<m)个AP获得的RSSI值, 使用F表示一个线性操作,这个线性操作将空间中的像素表达转换成频域的系数表达,即
| $ x = F{r_i}. $ | (2) |
定义一个选择矩阵GM×N,用g′来表示G的每一行,是一个1×N的向量,所有元素都是0,除了g(n)=1,n是离线阶段被测量的AP节点的下标.简单来说,对某个位置而言, AP点的选择是无序的.
因此离线阶段的RSSI向量表示为
| $ \mathit{\boldsymbol{m}} = \mathit{\boldsymbol{G}}{r_i} = \mathit{\boldsymbol{G}}{F^{-1}}x = \mathit{\boldsymbol{R}}. $ | (3) |
因为x是稀疏的,可以使用如下公式对其正交,
| $ \mathit{\boldsymbol{T}}{\rm{ = }}\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{R}}^{\rm{\dagger }}}. $ | (4) |
| $ \mathit{\boldsymbol{z}} = \mathit{\boldsymbol{Tm}} = \mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{R}}^{\rm{\dagger }}}\mathit{\boldsymbol{R}}x. $ | (5) |
其中Q=(RT)是正交化矩阵,R†是R的伪逆矩阵,使用全变分最小化[14]进行求解如下:
| $ \hat{x}=\rm{argmin}{{\left\| \triangledown \left(\mathit{x} \right) \right\|}_{\rm{1}}}\rm{s}.\rm{t}.\mathit{\boldsymbol{z}}\rm{=}\mathit{\boldsymbol{Q}}\mathit{x}+\varepsilon , $ | (6) |
其中‖▽(x)‖1是总方差,ε是噪声测量值,第i样本点的RSSI值可以表示为
| $ {r_i} = {F^{-1}}x. $ | (7) |
位置指纹库R中其他的样本点能够以同样的方式被恢复.
2 采用重心拉格朗日插值法构建位置指纹库在室内复杂的无线信号环境下,伴随着强烈的信号衰落和多径效应,很难建立一个符合实际应用的电磁波传播模型.目前较多应用的经验模型包括WAF模型和对数路径距离函数模型[17].
对数路径距离函数模型如下:
| $ P\left( d \right)\left[{{\rm{dB}}} \right] = P\left( {{d_0}} \right)\left[{{\rm{dB}}} \right] -10n{\rm{lg}}\left( {\frac{d}{{{d_0}}}} \right) + {X_\sigma }. $ | (8) |
其中P(d)表示接收端接收到的信号强度,P(d0)表示在参考距离接收到的信号强度值,这是一个参考量.d0表示参考距离,d表示实际距离,n表示发射端到接收端之间的障碍因子,Xσ是高斯分布随机量.n和Xσ的值通过采集RSSI值拟合计算获得.
但在多次实际测量中,无线信号的经验模型并不完全符合实测数据,尤其是在距离较远的地方.基于此, 首先建立样本点RSSI值和距离的关系方程为
| $ {\rm{RSS}}{{\rm{I}}_i} = L\left( d \right). $ | (9) |
其中RSSI表示样本节点与锚节点之间的信号强度值,d表示样本节点与锚节点之间的距离.笔者事先在定位空间中选取k+1个样本点,其中k+1<n(n为样本点的总数),测量出它们与样本节点的距离和RSSI值如下:
| $ \left( {{d_0}, {\rm{RSS}}{{\rm{I}}_{i0}}} \right), \left( {{d_1}, {\rm{RSS}}{{\rm{I}}_{i1}}} \right), \cdots \left( {{d_k}, {\rm{RSS}}{{\rm{I}}_{ik}}} \right). $ |
构建重心拉格朗日插值函数如下:
| $ L\left( x \right) = \frac{{\sum\nolimits_{j = 0}^k {\frac{{{w_j}}}{{x-{x_j}}}} {y_j}}}{{\sum\nolimits_{j = 0}^k {\frac{{{w_j}}}{{x-{x_j}}}} }}. $ | (10) |
其中,wj是插值重心权,
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\;\;\left( {{d_{k + 1}},L\left( {{d_{k + 1}}} \right)} \right),\left( {{d_{k + 1}},L\left( {{d_{k + 1}}} \right)} \right),\cdots \left( {{d_{n - 1}}} \right.,}\\ {\left. {L\left( {{d_{n - 1}}} \right)} \right).} \end{array} $ |
在上述构建位置指纹库的方法中k的选取很重要,如果k的取值较小,则难以描述出定位空间的RSSI值分布;如果取值较大,则失去插值法的意义,除此之外k的取值还必须满足均向性.
3 模糊位置指纹定位算法采用压缩传感理论和重心拉格朗日插值算法,可分别建立三维位置模糊指纹库,在线阶段使用模糊匹配的方式,那么每个未知节点测出的RSSI值至少可以匹配一个样本点,从而避免了无解的情况.任意一个未知点s,获取了自身与锚节点的RSSI值后,将得到一个采样向量Rs={rs1, rs2, ..., rsm}.
由模糊识别理论可以计算出Rs隶属于哪一个样本点.
首先将采样向量Rs与n个样本的向量表达式进行归一化,即
| $ \sum\limits_{j = 1}^m {{r_{ij}} = 1, i = 1, 2, 3 \cdots n{\rm{且}}} \sum\limits_{j = 1}^m {{r_{sj}} = 1.} $ | (11) |
然后采用欧几里德贴近度公式计算贴近度:
| $ \left( {{\mathit{\boldsymbol{R}}_i}, {\mathit{\boldsymbol{R}}_s}} \right) = 1-\sqrt {\frac{1}{m}{{\sum\limits_{j = 1}^m {\left( {{r_{ij}}-{r_{sj}}} \right)} }^2}}, $ | (12) |
其中(i=1, 2, …).
最后对所求得的αi=(Ri, Rs)进行排序,选取与s点贴近度最高的4个样本.再根据这4个样本点坐标位置的贴近度加权系数计算出未知节点的具体位置坐标.
设具有最高贴近度的4个样本点的贴近度依次是α1、α2、α3、α4.利用贴近度加权系数求取未知节点的坐标(X0, Y0, Z0).
| $ {X_0} = \sum\limits_{i = 1}^4 {{\beta _i}{X_i}}, $ | (13) |
| $ {Y_0} = \sum\limits_{i = 1}^4 {{\beta _i}{Y_i}}, $ | (14) |
| $ {Z_0} = \sum\limits_{i = 1}^4 {{\beta _i}{Z_i}}, $ | (15) |
其中,βi是第i(i=1…, 4) 个样本节点的贴近度加权系数.
| $ {\beta _i} = \frac{{{\alpha _i}}}{{{\alpha _{{\rm{sum}}}}}}, $ |
其中
本次实验选取广东工业大学工学一号馆的5楼空间作为实验区域(约100m×25m),如图 1所示.其中A区和B区是镂空区域,不存在定位需求.
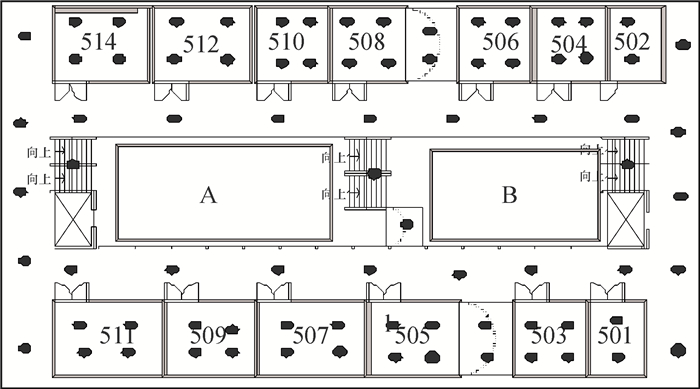
|
图 1 定位区域 Figure 1 Location area |
为了验证本方案的定位精度以及实验的可重复性,在定位区域布置80个AP点作为测量插值样本节点的RSSI值的发射器,如图 1所示.分别根据重心拉格朗日差值法和压缩传感对位置指纹库R进行恢复.然后根据本文中提供的模糊位置指纹定位算法计算得到位置估计.
具体实验如下:
80个AP摆在定位区域的任意位置,其坐标是确定的,在离线采样阶段,在定位空间中选取m(n<m)个点作为样本点,再从样本点中选取K个点作为重心拉格朗日插值样本点(0<K<m), 在每个插值样本点测量20次RSSI值,然后通过高斯滤波法得到每个插值样本点最终的RSSI值,由此建立起插值样本点定位指纹库R1,上位机通过重心拉格朗日插值算法对样本节点进行插值计算建立位置指纹库Rl.由于压缩传感适用于稀疏向量恢复,笔者在80个锚节点中随机选取ξ(ξ<80) 个锚节点, 对于每一个样本节点,进行信号恢复,最终得到恢复的位置指纹库Rc,分别比较Rl和Rc与经过实测得到的位置指纹库R的差异,最后根据位置指纹定位得到3种方法的误差比较.
4.2 实验过程 4.2.1 重心拉格朗日插值插值样本点的个数与样本点个数的选取对于插值的性能都有影响,依循等距的原则,在实验区域布置100个样本点.在此基础上笔者首先选取50个插值样本点进行计算,由于定位的区域较大和硬件条件的限制,样本节点不一定能够接收到所有锚节点的信号,如果信号缺省,以0作为此次接收到的RSSI值.分别改变插值样本点和样本点的个数,利用类似公式(16) 计算出插值误差,得到的实验结果如图 2所示,可以看出当样本点的数量保持不变,而增加插值样本点的数量时,平均误差随之减小;当插值样本点的数量不变时,增加样本点的数量,插值误差并没有出现明显的变化.表明重心拉格朗日插值算法在室内定位环境具备较好的稳定性.
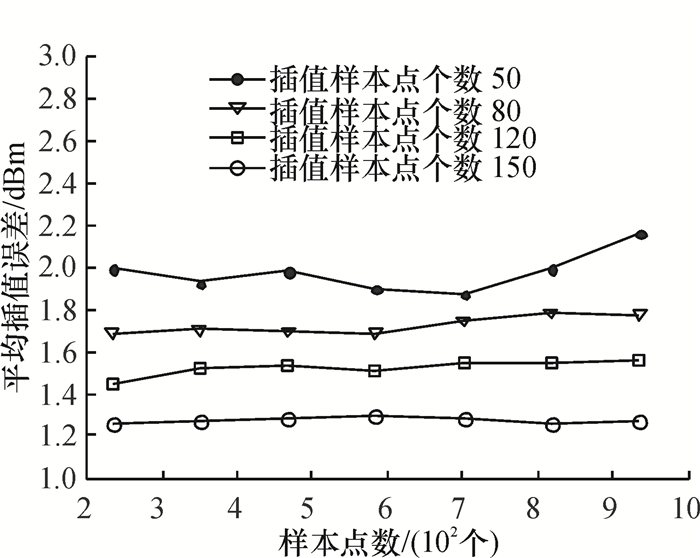
|
图 2 重心拉格朗日插值误差 Figure 2 The error of focus gravity Lagrange interpolation |
根据图 3可以看出在锚节点数为80、插值样本点数改变的情况下,重心拉格朗日插值算法较之于三次样条插值和分段插值在实验环境中具备明显的优势.
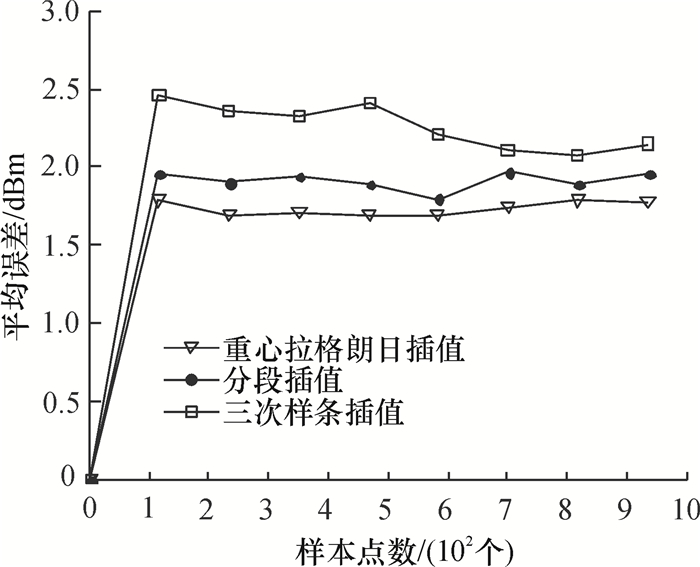
|
图 3 不同插值算法误差比较 Figure 3 The compression error of different interpolation algorithm |
为了减少在建库阶段需要测量的次数,可以通过压缩传感来重建位置指纹库.2.4G上802.11b/g的网络的波长是10~50m,在实验中,锚节点的布置间隔至少是1.5m.这说明位置指纹库并没有捕捉到方差,可以使用压缩传感理论进行信号恢复.随机选择20个AP点进行仿真实验,逐渐增加AP节点的数量,观察恢复结果如图 4所示, 用式(16) 计算出误差平均值e.
| $ e = \frac{1}{{N \times L}}\sum\limits_{i = 1}^L {\sum\limits_{j = 1}^N {\left| {{\mathit{\boldsymbol{R}}_{i, j}}-{{\mathit{\boldsymbol{\hat R}}}_{i, j}}} \right|} } $ | (16) |
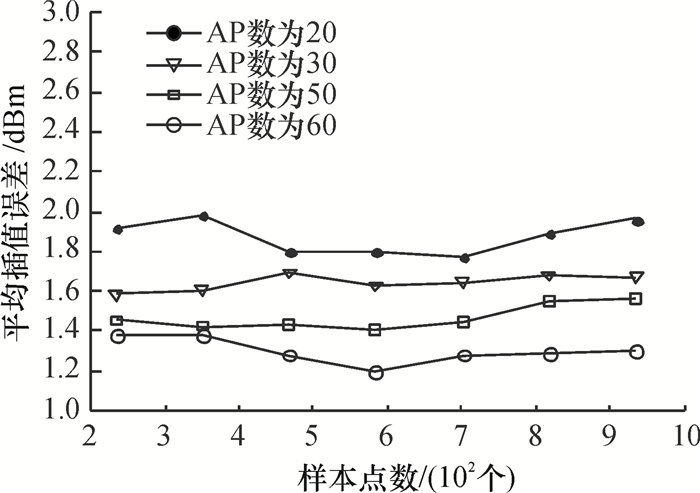
|
图 4 压缩传感指纹恢复误差 Figure 4 The error of compressed sensing fingerprint recovery |
其中,L是样本点数,N是未测量的样本点,
如图 4所示,当AP节点增加时,平均误差逐渐减小,指纹向量恢复的效果越好.
4.2.3 模糊位置指纹定位在图 1所示的定位区域随机布置100个未知点进行实验,分别使用压缩传感与重心拉格朗日插值法构建位置指纹库.同时实测构建位置指纹库.使用3种指纹库进行定位实验.预置条件如表 1所示.
| 表 1 算法的预置条件 Table 1 The preset conditions of the algorithm |
由图 2可得到样本点数为500,插值样本点数为80时,指纹向量平均误差是1.68 dBm.由图 4可知,在样本点个数为500,AP点的个数为50时,指纹向量的平均误差是1.47 dBm,两者的差距接近.将以上两种算法建立的指纹库与实测建立的指纹库进行定位试验,在线阶段采用模糊位置指纹定位算法.分别记录下100个试验点的平均定位误差如图 5所示.
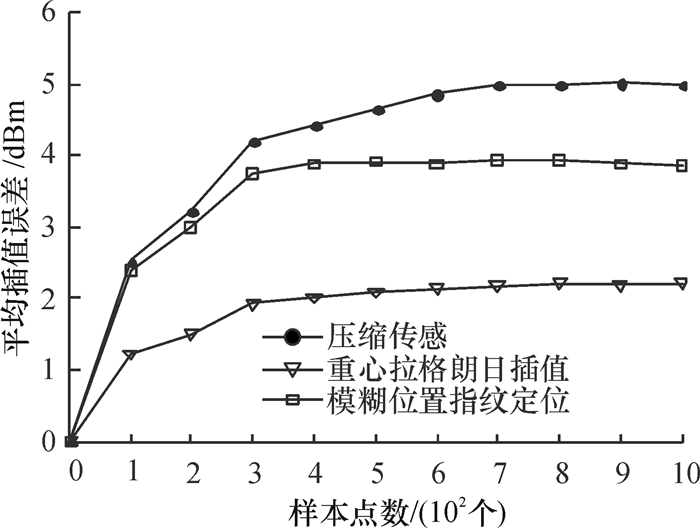
|
图 5 定位误差比较 Figure 5 The compression position error |
根据图 5,利用实测得到的位置指纹库进行定位的平均误差低于利用压缩传感理论指纹库和重心拉格朗日插值指纹库进行定位的平均误差.实测指纹库的定位误差平均值是2.216 7m.压缩传感指纹库的平均定位误差是3.636 9m, 低于重心拉格朗日插值算法的4.972 6m, 且有80%的未知点的定位误差在4m内.压缩传感指纹库比重心拉格朗日指纹库具备更加稳定的定位性能.
5 结语本文在现有的位置指纹定位算法基础上,提出使用压缩传感和重心拉格朗日插值两种算法来更新位置指纹库,减少在离线阶段所需耗费的人力和物力.同时在线定位阶段还引入了模糊匹配、模糊决策的思想.实际环境实验表明利用压缩传感理论构建的位置指纹库的定位性能高于重心拉格朗日插值算法建立的指纹库.然而,由于室内环境的复杂性,实验过程中的样本需求多样化,算法的自适应能力不高,这些问题将在以后的研究中改进.由于模糊匹配算法在位置指纹定位算法中有良好的效果,今后可将该算法应用于其他室内定位的场景.
| [1] | HUANG J, MILLMAN D, QUIGLEY M, et al. Efficient, generalized indoor WiFi GraphSLAM[C]// Robotics and Automation (ICRA), 2011 IEEE International Conference on.Shanghai:IEEE, 2011:1038-1043. |
| [2] |
孙晓玲, 李伟勤. 基于RFID的二维室内定位算法的实现[J].
现代电子技术, 2010(24): 90-92.
SUN X L, LI W Q. The implementation of 2-D indoor location algorithm based on RFID[J]. Journal of Modern Electronic Technology, 2010(24): 90-92. DOI: 10.3969/j.issn.1004-373X.2010.24.029. |
| [3] |
高睿劼, 黄鲁, 朱警怡. UWB室内定位系统的射频收发机设计[J].
微型机与应用, 2013(13): 87-89.
GAO R J, HUANG L, ZHU J Y. Design of RF transceiver in UWB positioning system[J]. Micro Computer & Applications, 2013(13): 87-89. DOI: 10.3969/j.issn.1674-7720.2013.13.025. |
| [4] | 张顺扬. ZigBee无线传感器网络研究及仿真[D]. 广州: 广东工业大学信息工程学院, 2008. |
| [5] |
王睿, 赵方, 彭金华. 基于WI-FI和蓝牙融合的室内定位算法[J].
计算机研究与发展, 2011, 4(S): 28-33.
WANG R, ZHAO F, PENG J H. Combination of WI-FI and bluetooth for indoor localization[J]. Journal of Computer Research and Development, 2011, 4(S): 28-33. |
| [6] | 刘金龙. 无线传感器网络TDOA定位算法研究[D]. 哈尔滨: 哈尔滨工业大学电子与信息工程学院, 2011. |
| [7] | WONG C M, MESSIER G G, KLUKAS R. Evaluating measurement-based AOA indoor location using WLAN infrastucture[C]//20th International Technical Meeting of the Satellite Division of the Institute of Navigation. Texas:Fort Worth Convention Center:[s.n.], 2007, 4:1139-1145. |
| [8] |
杨博雄, 倪玉华, 刘琨, 等. 基于加权三角质心RSSI算法的ZigBee室内无线定位技术研究[J].
传感器世界, 2012(11): 31-35.
YANG B X, NI Y H, LIU K, et al. Study on ZigBee wireless location technology based on weighting triple centroid RSSI algorithm[J]. Sensor World, 2012(11): 31-35. DOI: 10.3969/j.issn.1006-883X.2012.11.005. |
| [9] | 朱山. 室内无线传播及覆盖性能研究[D]. 武汉: 华中科技大学电子信息与通信学院, 2012. |
| [10] |
朱剑, 赵海, 林凯, 等. 基于WSNs的模糊三角形定位模型研究[J].
东北大学学报, 2010, 31(1): 35-38.
ZHU J, ZHAO H, LIN K, et al. Research on the fuzzy triangular localizationmodel in WSNs[J]. Journal of Northeastern University, 2010, 31(1): 35-38. |
| [11] | LI B, WANG Y, LEE H K, et al. Method for yielding a database of location fingerprints in WLAN[J]. Communications, IEE Proceedings, 2005, 152(5): 580-586. DOI: 10.1049/ip-com:20050078. |
| [12] |
权双燕, 曹阳. 插值法的应用与研究[J].
科技信息, 2007(36): 413-414.
QUAN S Y, CAO Y. Interpolation method research and application[J]. Science & Technology Information, 2007(36): 413-414. |
| [13] |
李树涛, 魏丹. 压缩传感综述[J].
自动化学报, 2009, 35(11): 1369-1377.
LI S T, WEI D. A survey on compressive sensing[J]. Acta Automatica Sinica, 2009, 35(11): 1369-1377. |
| [14] | TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666. DOI: 10.1109/TIT.2007.909108. |
| [15] |
娄静涛, 李永乐, 谭树人, 等. 基于全变分的全向图像稀疏重构算法[J].
电子学报, 2014, 44(2): 243-249.
LOU J T, LI Y L, TAN S R, et al. Sparse reconstruction for omnidirectional image based on total variation[J]. Acta Electronica Sinica, 2014, 44(2): 243-249. |
| [16] | BLUMENSATH T, DAVIES M E. Iterative thresholding for sparse approximations[J]. Journal of Fourier Analysis and Applications, 2008, 14(5-6): 629-654. DOI: 10.1007/s00041-008-9035-z. |
| [17] | 叶蔚. 室内无线定位的研究[D]. 广州: 华南理工大学电子与信息学院, 2010. |
| [18] |
彭越, 吴多龙, GuillaumeAndrieux, 等. 基于最小能量法的无线传感器网络节点能量有效性研究[J].
广东工业大学学报, 2014, 31(1): 86-89.
PENG Y, WU D L, ANDRIEUX G, et al. Research on energy-efficiency in wireless sensor networks based on minimum energy coding[J]. Journal of Guangdong University of Technology, 2014, 31(1): 86-89. |
| [19] |
鲁叶, 彭世国. T-S模糊随机时滞系统的鲁棒控制[J].
广东工业大学学报, 2013, 30(1): 68-72.
LU Y, PENG S G. Robust control of T-S fuzzy stochastic system with time-delay[J]. Journal of Guangdong University of Technology, 2013, 30(1): 68-72. |
 2016, Vol. 33
2016, Vol. 33