微博作为社交网络的重要平台之一，已经成为人们进行交流的主要媒介.在微博社区中，用户受到的关注度的高低同其影响力的大小密切相关，用户的影响力越大，其受到关注的程度越高，从而对整个社交网络产生的影响越大.因此，对用户影响力进行量化与排序已经成为社会学^[1-2]、心理学、新闻传播学等领域的研究热点.

PageRank算法^[3]是研究用户影响力的一种基本方法，该算法通过网页的链接结构来度量网页的重要性，谷歌公司已经将其应用到Twitter^[4]用户的排名中^[5].YAMAGUCHI^[6]基于微博网络图提出了Twitter用户排名(TURank)算法，该算法只考虑了微博的内容，但是忽略了其他用户对内容的进一步处理.针对PageRank算法没有考虑主题对排序结果的影响，T. Havdiwala H等^[7]对其进行了改进，改进的算法以网络的拓扑结构为度量基础，还加入上下文相关性和主题敏感度等影响因素.康书龙等^[8]通过分析新浪微博用户的行为和关系提出了一个更先进的算法来评估用户的影响力，但是该算法只考虑了发布微博的频率，忽略了用户间的交互行为带来的影响，实验证明这些因素同样会对用户的影响力产生较大的影响.CHA等^[9]提出了评估用户影响力的3个要素：粉丝数量，转发次数和被提及次数.针对这三方面的度量要素研究了基于主题和时间的动态性的用户影响力，发现有影响力的用户可以同时在很多主题上保持较高的影响力.国内学者中，陈浩^[10]提出的UserRank算法从用户自身质量及其追随者(即follower)质量入手, 考虑追随者数量，但是其文中并没有突出转发，评论等行为的重要性.并且，近年来，影响力最大化和基于主题的用户影响力研究也获得了极大的关注^[11-15].Weng J等^[16]提出的TwitterRank算法，不仅考虑网络结构与用户交互，还分析了主题的相似性并与现有的算法进行对比.

本文以用户作为切入点，同时对网络的拓扑结构和微博上的用户行为进行分析，提出了一种新的影响力评估模型——UIRank模型.

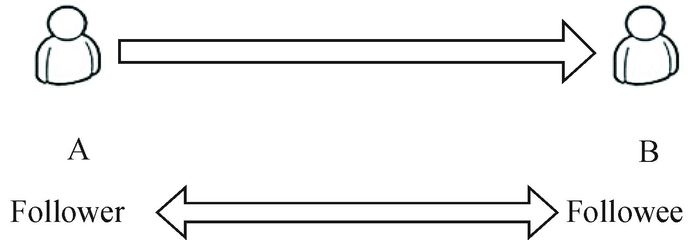
在微博中，一个用户可以在不经过其他用户允许情况下去“关注(follow)”另一个用户，其中，产生“Following”行为的用户被定义为“Follower”，而“Followed”的用户定义为“Followee”.微博用户之间的网络结构可以用一个有向图(见图 1)表示，图中的每一个节点代表一个用户，节点间的有向边代表用户之间的相互关系.本文使用G=(V, E)代表一个网络结构，其中V代表用户集合，E是有向边的集合.图 1中用户A“follow”用户B，即A是B的“Follower”，B是A的“Followee”.除了“关注”外，微博用户之间还存在其他交互行为，如转发(Retweet)、评论(Comment)和提及(Mention).

图 1(Figure 1)

图 1 微博网络中用户关系的描述图 Figure 1 The user relationship in the microblog network

研究表明，微博网络结构模型与网页链接模型相似，用户A“follow”用户B类似于网页A“vote”网页B.本文提出的影响力计算方法是基于经典的PageRank算法^[3].PageRank算法^[3]的计算基于以下两个基本假设.

1) 数量假设：在Web图模型中，如果链接到网页A的网页数量越多，那么网页A越重要.

2) 质量假设：根据链接到网页A的网页质量的不同决定网页A的重要性.如果越多高质量的网页指向网页A，则网页A越重要.

利用以上两个假设，PageRank算法初始化时赋予每个网页相同的重要性得分，通过迭代计算每个页面节点的PageRank值，直到收敛.即被越多优质的网页所指的网页，它是优质网页的概率就越大.

由于存在一些出链为0，没有链接指向任意其他网页的网页.因此需要对PageRank公式进行修正，即在原来的公式中增加了阻尼系数(damping factor)p，一般p取值0.85.其意义是，在任意时刻，用户到达某页面后并继续向后浏览的概率.则1-p=0.15表示用户停止点击，随机跳到新网页链接的概率.PageRank的计算公式如下：

本文根据微博网络结构模型与网页链接模型相似，对PageRank的假设进行修正，提出UIRank模型的两个假设.

假设1：如果一条微博被转发评论多次，那么可以认为它很重要.

假设2：一条微博被转发评论次数不高但是转发评论该微博的用户中包含高影响力用户，那么同样可以认为它很重要.

UIRank模型初始化方式为：首先，随机访问用户集合中的一个用户，然后根据当前用户的“follow”关系继续访问下一个用户.

本文充分考虑微博用户的不同行为，通过改进传统的PageRank算法评估微博的用户影响力，使得它更适合微博网络结构.

在PageRank算法中，每个网页将其当前的PageRank值平均分配到本网页包含的所有网页链接，这样将导致网页本身的重要性被忽略.所以在UIRank模型的分析过程中，将用户不同行为的权重作为分配UIRank值的依据.最终，活跃度高的用户影响力将会比活跃度低的用户高，这样可以弥补仅依赖“Follower”和“Followee”关系网络评估影响力的缺陷.UIRank模型的数学表示如下：

其中，p是阻尼系数，本文取值为0.5; M(u)是用户u的所有“Follower”的集合；A_{(v, u)}是用户v对用户u的UIRank值的贡献比率，表示用户u的行为权重占用户v的所有“Followee”的行为权重之和的比例，公式表达为

式(3) 中，W_u代表用户u的用户行为权重，N_v代表用户v的“Followee”数目(即用户v的出度).

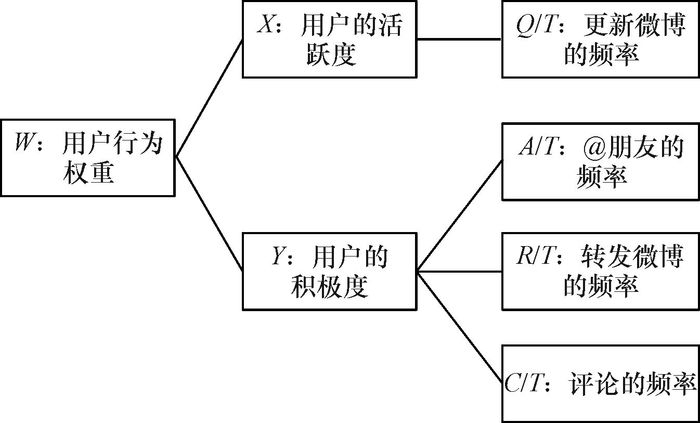
根据前面的描述，UIRank模型相比TunkRank等其他模型最大的改进是对用户不同行为做了充分的分析，将其作为影响力评估的重要指标.UIRank算法通过分析不同行为的权重分配UIRank值.其中，用户行为主要包括用户更新微博的频率，与其他用户的交互(评论，转发)等，将它们作为用户的活跃度和用户之间互动的积极度.图 2为用户行为权重模型.

图 2(Figure 2)

图 2 用户行为权重模型 Figure 2 The weight model of user behaviors

式(3) 中采用W_u代表用户u的行为权重，同时考虑用户活跃度和互动积极度，得

式(4) 中用户的活跃度X_i表示在一个时间段内用户更新微博的频率，用户的互动积极度Y_i表示在一个时间段内用户之间提到(Mention)，评论(Comment)和转发(Retweet)的交互频率.

其中，T表示一个时间段.为了更客观地描述用户的活跃度和积极度，T选取同一个时间段.P_i表示用户i发表的微博数目，A_i表示“@”的数量，C_i表示评论数，R_i表示转发数，c，d，e分别表示加权系数.根据对UIRank模型的分析可知，用户行为对权值的影响不同，加权系数也不同.本文使用序关系分析法确定UIRank算法中权重系数，序关系分析法的定义如下.

定义1 若评价指标X_i相对于某评价目标的重要性程度大于X_j时，记为X_i > X_j.

在序关系分析法中，不同评价指标之间存在数量约束r_k，r_k的确定满足如下的两个定理.

定理1 若评价指标X₁, X₂, X₃…, X_m之间存在序数关系X₁>X₂>X₃…>X_m, 则r_k与r_k-1之间必须满足，r_k-1>1/r_k.

定理2 若给出的数量约束满足定理1，那么各评价指标的权重${\omega _m} = {\left( {1 + \sum\limits_{k = 2}^m {\sum\limits_{i = k}^m {{r_i}} } } \right)^{ - 1}}$，而ω_k-1=r_k·ω_k.

通过上文用户行为的分析，微博作为一个交互网络，用户之间的交互行为比用户发微博的行为更具影响力，而在用户交互行为中评论行为将作为首要因素，基于序关系分析法，本文将作如下参数设置：a = 0.4，b = 0.6，c = 0.5，d = 0.3，e = 0.2.然后通过式(5) 和(6) 计算活跃度X_i和积极度X_j，最后得到用户行为权重W_i.UIRank的算法的基本描述如表 1所示.

表 1(Table 1)

表 1 UIRank算法基本描述 Table 1 A basic description of UIRank algorithm 算法描述 输入: G=(V, E), PROFILES, ACTIONS, a, b, c, d, e; 输出:每个用户的UIRank值; 1: for节点集合V中的每一个节点v; 2:分别计算每个节点的Xi, Xj，Wi值; 3:结束循环; 4: while (ratio > 10-10); 5: for＜v，u>计算用户v对用户u的UIRank值的贡献比率A(v, u); 6: for每一个v∈ M(u); 7:计算得到UIRank(v); 8:对于步骤7和9计算得到的值相乘求总和； 9:结束for循环； 10:通过计算公式计算UIRank(u)； 11:结束for循环； 12:当ratio＜10-10时，结束while循环.

表 1 UIRank算法基本描述 Table 1 A basic description of UIRank algorithm

腾讯微博自2010年4月创建以来已经成长为国内最大的微博网站之一.当前，腾讯微博注册用户超过两亿，每天产生超过4千万条微博信息，为保证本文使用腾讯微博的数据集更具有说服力，本文使用的数据集来自国际知识发现和数据挖掘竞赛(KDD Cup).在进行实验之前，本文先对数据进行预处理，剔除数据集中的冗余样本以及不完整样本，最终得到包含60 000多个用户的样本集.数据集中各字段描述如表 2所示.

表 2(Table 2)

表 2 数据集中各个字段含义 Table 2 The meaning of each field in the dataset 字段 含义 UserID 用户的ID Birth 生日 Gender 性别 Num_Followee “Followee”的个数 Num_Follower “Follower”的个数 FollowerID “Follower”的ID Num_Tweet 发布的微博信息的数目 Num_At “@”行为的数目 Num_Retweet 转发行为的数目 Num_Comment 评论行为的数目 Num_Action 产生交互行为的朋友数目

表 2 数据集中各个字段含义 Table 2 The meaning of each field in the dataset

为了证明UIRank算法的准确性，本文采用TunkRank算法在相同的数据集上进行实验并作对比.TunkRank算法的数学描述如式(7) 所示，p值取0.2.

其中，Followers是v的所有“Follower”，Followees是v的所有“Followee”.

表 3和表 4展示了通过TunkRank和UIRank两种算法在相同数据集上找到的排名前十的最有影响力的用户，可以观察到在两个表中有7个用户是重叠的.在UIRank算法中，用户1010402，用户640892和用户330571成为进入前十的新用户，它们原来在TunkRank算法中分别排第11位，第39位和48位.他们能够进入前十的原因各不相同.虽然被其他人提到的次数少，但是用户1010402获得相对较大数量的转发行为.对于用户640892和330571，他们分别被4个和3个排名前十的用户“follow”，弥补了追随者少和交互少的缺陷.此外，用户1774520排名高于用户1775076的原因是他/她与他人互动频繁.通过本文提出的UIRank算法得到影响力排名前30名用户中，有22个用户被排在第一位的用户1928699“follow”.因此，对比两种方法的实验结果可知TunkRank算法严重依赖“follower”的数量和质量，UIRank算法不但考虑“Follower”的因素还进一步考虑用户间的行为交互，更加合理准确.

表 3(Table 3)

表 3 TunkRank算法排名前10的最有影响力的用户 Table 3 The top 10 most influential users in TunkRank algorithm 排名 用户ID 粉丝数 转发次数 评论次数 “@”次数 1 1928699 60 662 76 832 972 3 762 2 1775076 19 855 121 215 4 443 2 310 3 1760642 15 653 109 450 22 983 10 717 4 2105598 14 750 100 063 2 310 2 310 5 1902321 9 098 22 847 2 063 6 919 6 2188303 12 319 432 334 22 166 9 409 7 332673 11 360 38 056 1 532 3 231 8 1774849 12 386 22 450 2 513 1 901 9 1774520 10 640 142 779 13 724 10 788 10 131665 7 303 57 341 2 435 6 864

表 3 TunkRank算法排名前10的最有影响力的用户 Table 3 The top 10 most influential users in TunkRank algorithm

表 4(Table 4)

表 4 UIRank算法排名前10的最有影响力的用户 Table 4 The top 10 most influential users in UIRank algorithm 排名 用户ID 粉丝数 转发次数 评论次数 “@”次数 1 1928699 60 662 76 832 972 3 762 2 1010402 8 493 5 129 005 46 712 78 3 1760642 15 653 109 450 22 983 10 717 4 1774520 10 640 142 779 13 724 10 788 5 1902321 9 098 22 847 2 063 6 919 6 640892 1 977 11 066 372 52 7 2188303 12 319 432 334 22 166 9 409 8 332673 11 360 38 056 1 532 3 231 9 1775076 19 855 121 215 4 443 2 310 10 330571 890 15 173 407 96

表 4 UIRank算法排名前10的最有影响力的用户 Table 4 The top 10 most influential users in UIRank algorithm

在2.2中验证了UIRank模型的有效性，本部分将验证通过UIRank模型挑选出的最有影响力用户的正确性.因为本文使用的数据集中用户经过了匿名处理，不能得到他们在微博中真实的用户名，所以，本文采用与引文^[17]中影响力最大化相似的评估方法.基于上一部分选出的最有影响力的10个用户，仿照网络中信息传播度量的方法得到最后被激活(activated)的用户数目.最后本文根据不同方法激活的用户数目进行对比.首先发现通过UIRank模型得到的影响力的取值范围是0到1，这个数值反映了一个用户对另一个用户产生影响的程度.由于本文的主要目的不是计算信息传播概率，根据引文^[17]可知本文将UIRank值作为传播概率是合理的，本文选取TunkRank，PageRank和MaxDegree方法进行对比分析，以此验证通过UIRank方法得到的结果是准确的.

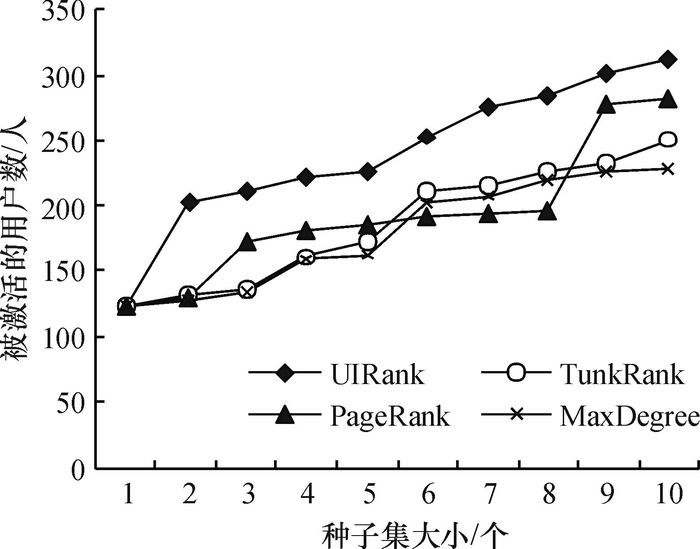
基于引文^[17]本文首先将种子集合的大小标记为k，对应的种子集中包含最有影响力的k个用户，再根据1到10的排名，本文添加下一个最有影响力的用户到种子集中，每一次的实验结果都进行了10 000次的模拟，图 3中可以看到所有方法的趋势都是上升的，但是每一次通过本文中的方法选中的k个用户激活的用户最多，这样就可以证明本文提出的方法是最有效的，并且选出的用户确实是最有影响力的.

图 3(Figure 3)

图 3 不同方法激活用户数对比图 Figure 3 The contrast of different approaches to activating users

本文通过考虑用户之间的行为交互对PageRank算法进行改进，提出一个新的模型来对用户影响力进行分析，并与TunkRank算法进行比较，进一步分析它们之间的差异.最后，本文将几个著名的算法选为基线，使用影响最大化来验证算法的有效性.实验结果表明，本文算法的结果更加准确和高效.

由上面的分析可以得到以下结论：(1) 一般情况下，追随者的数量和质量在一定程度上影响用户的影响力；(2) 用户影响力和用户与他人的交互行为密切相关，而且不同交互行为对他人影响力的贡献是不一样的；(3) 一些用户即使在追随者“Follower”数量和交互(Interaction)上有劣势，但当这些“follower”拥有很大的影响力值时，也会使这些用户获得很大的影响值.

本文中提出的UIRank模型可以合理准确地计算微博用户的影响力，对于市场营销，舆情控制等方面都有重要的现实意义.高质量的微博内容将更有利于传播，但是本文的UIRank模型并没有对微博内容本身进行分析.这个问题是后续研究的重点.