近年来，国内外各类大规模自然灾害频繁发生，因其具有严重次生灾害等特点, 给受灾地区带来了极大的人员伤亡以及严重的经济损失，同时在灾后救援过程中的不计成本、盲目救援造成了严重浪费.大规模自然灾害发生后，如何有效地在救援物资供应地安排车辆进行装载，如何选择车辆路径快速运输、分配应急救援物资，成了大规模应急救援物资配置的关键问题，是快速挽救生命、减少灾民损失、降低经济损耗的基本途径.

针对如何优化应急物资配送这一问题，国内外学者进行了大量有意义的研究.Sheu^[l]探讨总结了当前应急物资配置面临的挑战，并针对救援关键时期研究了面向大规模灾难的应急救援物资的配送方法；Chang和Tseng等^[2]针对洪灾发生后，受灾地区应急物资需求量不确定的问题，提出了适应不同灾情信息的应急救援物资配送的模型；郑斌和马祖军等^[3]建立了一个应急救援物资需求量不精确的多目标LRP优化策略；徐玖平等^[4]对汶川特大地震灾后应急救援物资配置问题进行了重建物资分配、运输、配送中转地选择等一系列的实证研究；陈刚和张锦等^[5]考虑了以应急物资保障过程为单目标的应急物资运输—配送模型；詹沙磊和刘南^[6]研究了多个物资供应点、多个受灾点的应急救援车辆选址、路径优化、物资配送的多目标随机规划模型；廖成等^[7]构建了大规模的应急救援模型，并考虑了更有效的求解方法.

综上所述，国内外学者对受灾情况多变的应急救援物资配置问题，已经进行了各种意义深远的建模研究，并对相应模型提出了松弛的拉格朗日算法^[8]、启发式算法^[9-10]、遗传优化智能算法^[11-12]等多种适应不同环境的算法.但是由于突发的大规模事件这一类问题往往会造成灾后应急救援物资配送的情况复杂多变，很难研发出应急救援物资配置通用的数学优化模型与算法，且仍然有许多急需解决的问题.为此，本文基于应急物资急需量大的情况下，考虑把受灾点物资包装成标准单元物资，研究三层大规模应急救援物资配送策略，并使用遗传算法对模型求解获得近似最优的方案.

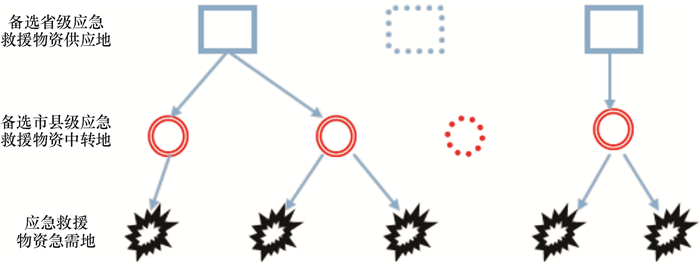
救援应急物资配送在受灾地区救援中最为关键，主要考虑问题是如何对受灾地区急需的物资包装分配以及如何安排装载车辆、选择运输路径对受灾地区进行救灾物资输送.因突发灾害复杂特殊、变化万千，对这一类情况特殊的救援应急物资配送问题，很难探讨出普遍适用的数学优化模型与算法.结合实际问题，本文考虑的网络简化结构如图 1所示.

图 1(Figure 1)

图 1 物资配送网络的简化结构 Figure 1 Simplified network structure of material allocation

本文以应急救援物资配置的总成本最小、应急救援物资总的运输时间最短、启用的供应地和中转地个数最少为目标，再应用基于加权排序的方法将3个目标转化为单目标函数，建立数学优化模型.目标函数min(f₁, f₂, f₃)中，

其中, 目标函数(1) 为应急救援物资配置的总成本，目标函数(2) 为应急救援物资总的运输时间，目标函数(3) 为启用的供应地和中转地个数.

目标转化：为了达到更好的救援效果，结合应急救援物资配置的实际问题，在现实应急救援物资配置中，决策者一般更加注重目标函数(2).采用基于加权排序的方法，根据应急救援物资配置的总成本、总的运输时间、启用的供应地和中转地个数这三者的重要性，取权重为λ₁=0.3，λ₂=0.5，λ₃=0.2.将以上3个目标聚集成一个单目标.

转化后目标函数：

约束条件：

其中：L={i|i=1, 2, …, l}为救援应急物资急需地集合；M={j|j=1, 2, …, m}为备选市县级应急救援物资中转地集合；N={k|k=1, 2, …, n}为备选省级应急救援物资供应地集合；α_i(i=1, 2, …, l)表示第i个应急救援物资急需地的物资数量；c_ji表示第j(j=1, 2, …, m)个备选市县级应急救援物资中转地到第i(i=1, 2, …, l)个应急救援物资急需地的距离；d_kj表示由第k(k=1, 2, …, n)个备选省级应急救援物资供应地到第j(j=1, 2, …, m)个备选市县级应急救援物资中转地的距离.

x_j, y_k, u_ji, r_kj(其中i=1, 2, …, l; j=1, 2, …, m; k=1, 2, …, n)为0-1决策变量；如果启用第j个市县级救援物资中转地时x_j=1，否则x_j=0；如果启用第k个省级应急救援物资供应地时y_k=1，否则y_k=0；如果第i个应急救援物资急需地由第j个市县级应急救援物资中转地运输物资时u_ji=1，否则u_ji=0；如果第j个市县级应急救援物资中转地由第k个省级应急救援物资供应地供应物资时r_kj=1，否则r_kj=0.

X_ji, Y_kj, Z_k(其中i=1, 2, …, l; j=1, 2, …, m; k=1, 2, …, n)为整数决策变量.X_ji表示负责第j个市县级应急救援物资中转地到第i个应急救援物资急需地的车辆数量；Y_kj表示负责第k个省级应急救援物资供应地到第j个市县级应急救援物资中转地的车辆数量；Z_k表示安排在第k个省级应急救援物资供应地的车辆数量.

遗传算法是一种仿效自然界“物竞天择、适者生存”的进化算法.根据问题，将目标设计成一个适应度函数，把问题所有可能取的解编码为染色体，一系列的染色体构成一个种群.利用迭代的方式让各个染色体经过若干代的选择、交叉、变异等运算来交换种群染色体的信息，并根据适应度评估染色体，优胜劣汰，使其逐渐趋向问题的近似最优解.本文参考文献[13-17]，结合应急救援物资配置模型，提出算法流程如下.

(1) 设置最大的迭代代数Gen_max，种群规模K、交叉率p_c和变异率p_m.

(2) 对种群个体使用二进制遗传编码.每个染色体都由两个子串组成，长度为m+n；其中第1个子串的长度为对应的备选市县级应急救援物资中转地的个数m，基因位为0-1，1表示对应备选的中转地被启用，0表示对应的中转地不被启用；第2个子串的长度为对应的备选省级应急救援物资供应地的个数n；基因位为0-1，1表示对应备选的供应地被启用，0表示对应的供应地不被启用.给出算法流程如下.

(1) 初始群体的生成.本文采用英国Sheffield遗传算法工具箱的crtbase函数创建任意种群规模为K=100，个体长度为m+n的二进制离散随机种群，将其定义为一个矩阵，至此得到初始种群P(0).

(2) 适应度评估，根据适应度函数大小区分优劣，评估每个染色体的适应度，优胜劣汰.本文直接考虑模型转化后的单目标函数式，取Fitness(i)=1/f(i)为适应度函数，其中f(i)为第i条染色体的目标函数值.

(3) 采用轮盘赌法进行选择操作，从P(n)(其中n为迭代代数)中选择K个染色体进入下一代P(n+1).

(4) 采用单断点交叉进行交叉操作，根据交叉概率p_c=0.7判断各个染色体是否进行交叉，以促进遗传算法对解空间的搜索.

(5) 采用离散变异法进行变异操作，对(4) 交叉后的染色体根据变异概率p_m=0.02判断该基因是否进行变异，产生新一代P(n+1).

(6) 算法结束，如果代数n＞Gen_max，输出最优解；如果代数n≤Gen_max，重复(2).

随机抽取7个备选省级应急救援物资供应地，10个备选市县级应急救援物资中转地，30个应急救援物资急需地以及所需的应急救援物资数量.其中平均救援物资的单位质量：θ=3 kg/件，每辆车单位距离的运输时间：ε=0.015 h/km，单位距离运输单位物资质量的费用：δ=0.25元/(kg.km)，启用每个供应地、中转地的增设费用：ω=0.12百万元/个，每辆车的最大装载重：Ω=35 000 kg/辆.

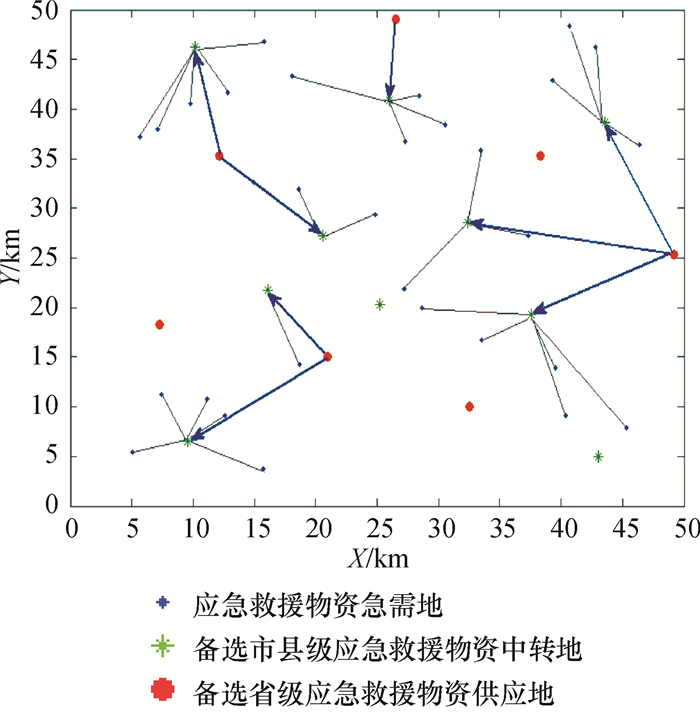
采用matlab软件，根据以上设计的遗传算法编写相应的程序，求解近似最优的算例结果为应急救援物资配置的总成本为6 691.8百万元，总的运输时间为20 635 h，启用的供应地和中转地数量为12个.其中车辆安排、路径选择、物资配送的近似最优结果见表 1、表 2和图 2.

表 1(Table 1)

表 1 启用的省级救援物资供应地以及物资配置策略 Table 1 The provincial supplying spot of selection and emergency material allocation strategy 启用的省级应急救援物资供应地/个 安排在此救援物资供应地的车辆数量/辆 由此救援物资供应地负责的市县级物资配送中转地/个 负责运输到此中转地的车辆数量/辆 运输到此中转地的应急救援物资数量/t 2 25 2 16 560 4 9 315 3 17 1 13 455 3 4 140 4 9 6 9 315 7 32 7 7 245 8 13 455 10 12 420

表 1 启用的省级救援物资供应地以及物资配置策略 Table 1 The provincial supplying spot of selection and emergency material allocation strategy

表 2(Table 2)

表 2 启用的市县级应急救援中转地以及物资配置策略 Table 2 The municipal and county-level transitional place of selection and emergency material allocation strategy 启用的市县级应急救援物资中转地/个 负责此中转地的车辆数量/辆 运输到此中转地的救援物资数量/t 由此中转地负责的应急物资急需地/个 负责运输到此中转地的车辆数量/辆 1 13 70 1 2 105 2 3 70 5 2 105 6 3 105 7 3 2 16 210 20 6 105 21 3 35 23 1 105 25 3 105 29 3 3 4 140 9 4 4 9 35 14 1 140 15 4 140 16 4 6 9 35 19 1 140 22 4 70 24 2 70 27 2 7 7 105 12 3 70 13 2 70 17 2 8 13 35 3 1 35 4 1 210 8 6 105 10 3 70 11 2 10 12 175 18 5 70 26 2 70 28 2 105 30 3

表 2 启用的市县级应急救援中转地以及物资配置策略 Table 2 The municipal and county-level transitional place of selection and emergency material allocation strategy

图 2(Figure 2)

图 2 算例目标函数近似最优的三层应急救援物资配置方案 Figure 2 The three-layer emergency material allocation strategy of approximate optimal objective function of example

本文是在受灾地区对应急救援物资急需量较大的基础上，基于全国范围这一大区域，以应急救援物资总的运输时间最短、配置的总成本最小、供应地和中转地启用个数最少为目标，考虑了包括备选省级应急救援物资供应地、备选市县级应急救援物资中转地、救援物资急需地三层结构的应急救援物资配置模型，研究了应急救援车辆安排、路径选择、救援物资配送的应急救援物资配置问题.最后结合遗传工具箱设计遗传算法求解获得近似最优的三层应急救灾物资配置方案.