受生物的智能行为启发，一些学者建立数学模型，模拟其寻优能力提出了多种智能优化算法.遗传算法^[1-4]是模拟自然界的生物选择、杂交、变异的进化过程的全局优化算法；粒子群算法^[5-7]是模拟鸟群觅食过程的一种有效的全局寻优算法.这类仿生算法不依赖于问题的具体领域，对问题的种类有很强的鲁棒性，为复杂系统优化提供了一种通用的求解框架，被广泛应用到函数优化^[8]、组合优化^[9]、自动控制^[10-11]、生产调度^[12]、图像处理^[13-15]等领域.

在长跑比赛中，运动员为了获得好的成绩，需要采用正确的战术策略.如何调整自己的步伐，是跟跑还是领跑, 冲刺时机选择等等都是比赛获胜的重要因素.长跑比赛实质就是追逐竞赛的过程.领先的运动员按自己的节奏，不断调整步伐奔向终点；落后的运动员结合自己的实力，设定视野范围，确定追逐目标，从而调整自己步伐，跟跑并超越对手.

借鉴追逐竞赛的过程，本文建立了数学模型并运用于优化问题的求解，提出了一种新的智能算法——模拟追逐算法.该算法通过追逐算子和探测算子作用，使个体不断调整步长，搜索到更优的位置，从而引导解不断地进化，最终实现全局寻优.数值实验验证了模拟追逐算法是一种有效的群体优化算法.

模拟追逐算法(Simulated Pursuit Algorithm, SPA)是模拟运动员长跑比赛的追逐过程行为所具有的智能性，为优化问题的解决提供了一种全局寻优算法.算法中运动员被称为“个体”或“解”，问题优化过程就是个体追逐过程.跑在比赛最前列的“个体”(最优个体)，为保持领先的位置，执行探测算子，尝试多次调整自己的步伐，计算出相应的新位置，若新位置优于原先位置，则选择较优的新位置替换最优个体位置，否则，最优个体位置保持不变.其他个体(非最优个体)执行追逐算子，首先个体根据战术需要，设定视野范围，确定追逐目标(个体)，若追逐目标数k>0, 则根据追逐目标，计算出需要调整的步长，确定新位置，若k=0，即视野范围内没有追逐目标，则参照最优个体的位置调整步长，计算新位置，直至群体完成设定的进化迭代次数，算法终止.

在模拟追逐算法中，关键参数是预先设定好的，参数设置对算法运行效率有很大的影响，具体包括种群大小N、当前迭代次数T_Cur、最大迭代次数T_Max、尝试次数m、视野范围r.

第i个个体位置为X_i，其适用度值为Y_i>0(如最小化问题，本文设定适用度函数为：Y_i=fitness(X_i)=M_max－f(X_i)，其中M_max取一个适当相对大的数，f(X_i)是目标函数值)，在视野范围为r内, 确定k个追逐目标，即$ S = \{ {X_j}|\left\| {{X_j}-{X_i}} \right\| \le r, 且{Y_j} \ge {Y_i}\} $，其中X_j为追逐目标，集合S中X_j的个体数为追逐目标数k.

步长Step为

其中Fector_j为追逐因子，$ G = {G_0} \cdot {{\rm{e}}^{\left( {-\alpha } \right) \cdot (\frac{{{T_{{\rm{Cur}}}}}}{{{T_{{\rm{Max}}}}}})}} $为追逐系数，其中G₀，α为追逐系数的参数.

由式(2) 和(3) 知, 被追逐个体X_j的适应度越大，Fector_j越大，对个体X_i位置更新所需的步长贡献率越大.所以

当k>0时，个体i的新位置为

否则k=0, 个体i的新位置为

其中step1=X_b－X_i，其中X_b为最优个体.

探测算子是通过一个随机扰动步长探测出最优个体可能的新位置.尝试次数为m, 步长生成源P>0, 向量维数为W.扰动步长Step 2随机生成, 其生成的代码(Matlab)为

最优个体的新位置X_b^*=X_b+step2, 尝试重复执行m次，得到m个新位置，然后选最好的新位置代替原来位置.注意：步长生成源P是一个动态的正数，搜索早期，期望扰动步长较大，有利于开拓进行全局搜索；搜索后期，期望扰动步长较小，有利于精细局部搜索.本文取P=P(1.01-T_Cur/T_Max).

模拟追逐算法步骤：

(1) 种群初始化与参数设置.

(2) 适应度计算，最优个体确定.

(3) 种群个体更新：若个体为最优个体，则执行探测算子；否则执行追逐算子.

(4) 算法终止条件是否满足，若满足，则算法结束；否则转步骤(2).

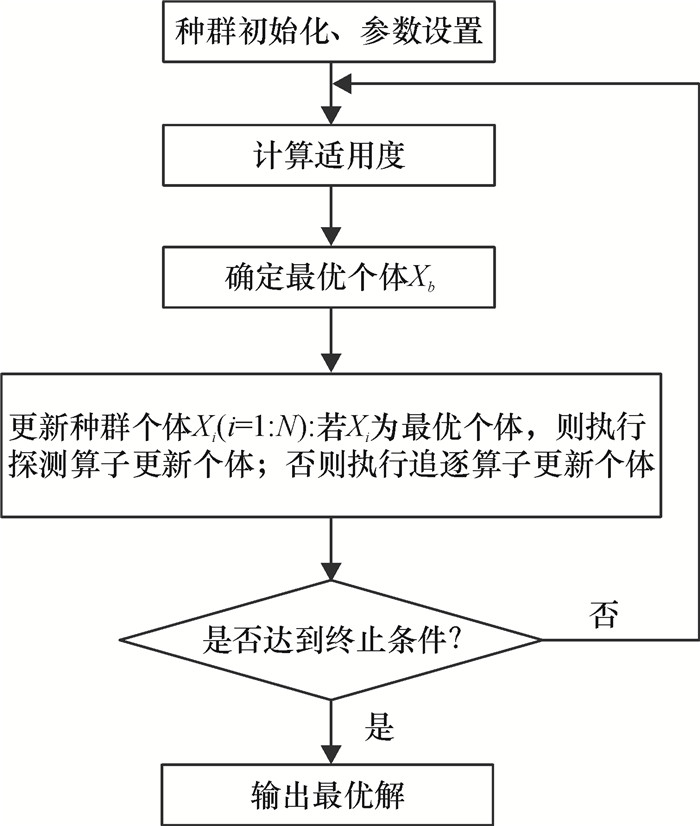
算法流程图如图 1所示

图 1(Figure 1)

图 1 模拟追逐算法流程图 Figure 1 Flow chart of SPA

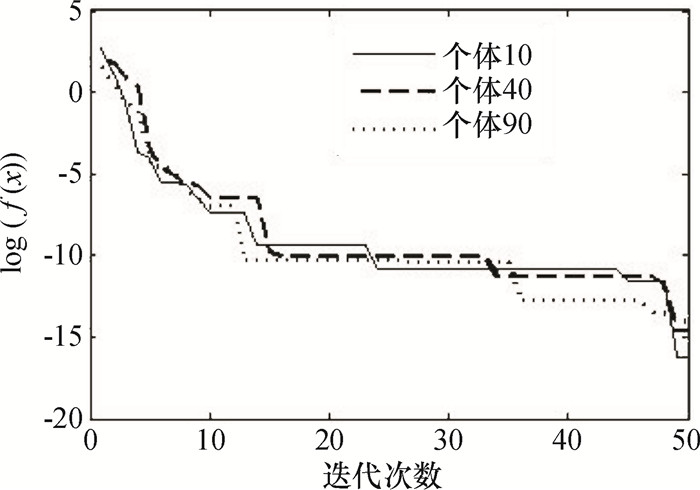
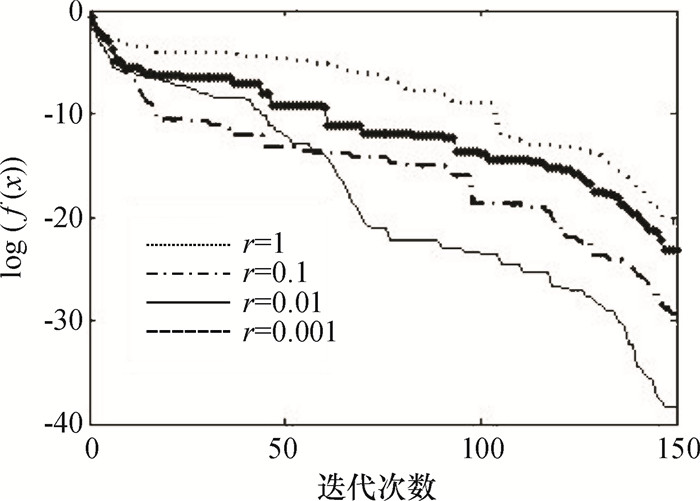
为分析追逐算子的功能，对个体为100，向量维数为5的种群，视野范围取不同值，执行追逐算子测试.图 2为随机选择编号为10，40，90的个体的50次迭代的进化曲线，图 3为视野范围r分别为0.000 1、0.01、0.1、1时，种群最优个体的进化曲线.结果表明：种群中的个体在迭代过程中不断进化，并具有跳出局部最优解的能力；同时追逐算子对解的搜索精度与收敛速度的影响与视野范围大小有关，视野范围为0.01时算子搜索效果最佳；视野范围的设置与优化问题有关.

图 2(Figure 2)

图 2 不同个体的进化曲线 Figure 2 Convergence curve of three individuals

图 3(Figure 3)

图 3 不同视野范围最优个体的进化曲线 Figure 3 Convergence curve of best individual

为了检验模拟追逐算法的优化性能，本文选择文献[4]的自适应遗传算法(记为GA), 文献[7]中的带粒子释放和速度限制的粒子群算法(记为PSO)与模拟追逐算法比较, 通过6个标准的测试函数(如表 1所示)测试3种算法的性能，数值实验在Matlab中完成.每个测试函数在相同条件下独立运行20次，记录最好结果、平均结果，算法成功率.

表 1(Table 1)

表 1 测试函数 Table 1 Test function 函数 表达式 区间 最优值 目标精度 f1 $ f\left( x \right) = \sum\limits_{j = 1}^5 {x_j^2} $ [-1.5, 1.5] 0 10－29 f2 $ f\left( x \right) = \sum\limits_{j = 1}^4 {[100{{({x_{j + 1}} - x_j^2)}^2} + {{({x_j} - 1)}^2}]} $ [-2, 2] 0 10－1 f3 $ f\left( x \right) = \sum\limits_{i = 1}^5 {\left[ {x_i^2 - 10\cos \left( {2\pi {x_i}} \right) + 10} \right]} $ [-15, 15] 0 10－∞ f4 $ f\left( x \right) = \sum\limits_{i = 1}^4 {{{\left( {x_i^2 + x_{i + 1}^2} \right)}^{0.25}}\left[ {{{\sin }^2}\left( {50{{\left( {x_i^2 + x_{i + 1}^2} \right)}^{0.1}}} \right) + 1} \right]} $ [-4, 4] 0 10－27 f5 $ f\left( x \right) = \frac{1}{{4000}}\sum\limits_{i = 1}^5 {x_i^2} - \prod\limits_{i = 1}^5 {\cos \left( {\frac{{{x_i}}}{{\sqrt i }}} \right) + 1} $ [-4, 4] 0 10－∞ f6 $f(x) = - 20\exp [ - 0.2\sqrt {\frac{1}{5}\sum\limits_{i = 1}^5 {x_i^2} } ] - \exp [\frac{1}{5}\sum\limits_{i = 1}^5 {\cos (2\pi {x_i})} ] + 20 + \rm{e} $ [-4, 4] 0 10－14

表 1 测试函数 Table 1 Test function

从表 2可知，为了获得更好的优化效果，视野范围r取值与优化问题相关；对于6个测试函数，无论是单峰函数还是多峰函数，SPA测试的最优值、平均最优值均优于GA与PSO, 说明新算法有很好的求解精度，特别是对于函数f₃与f₅，SPA均求解出理论最优值；对于6个测试函数分别设置其目标精度，除f₂外，其余5个优化问题求解成功率均为100%，说明SPA优化求解有很好的稳定性.

表 2(Table 2)

表 2 计算结果 Table 2 Computational results 函数 算法 参数取值 平均最优值 最好值 成功率/% G0 α r m f1 GA PSO SPA 100 10 0.05 5 7.459 5×10-5 5.170 6×10-22 1.242 2×10-29 4.021 5×10-6 6.329 2×10-26 8.473 0×10-31 0 0 100 f2 GA PSO SPA 120 20 0.005 16 3.934 0 2.789 1 0.972 1 3.714 3 2.645 7 0.895 1 0 0 62.5 f3 GA PSO SPA 50 20 0.25 16 0.406 0 0.165 8 0 0.344 3 8.880 0×10-15 0 0 50 100 f4 GA PSO SPA 50 10 0.25 5 1.193 0 0.080 9 1.309 3×10-28 0.515 1 3.950 9×10-6 2.710 6×10-31 0 0 100 f5 GA PSO SPA 50 20 0.25 20 0.001 2 0 0 0.394 0×10-4 0 0 0 100 100 f6 GA PSO SPA 50 80 0.5 20 0.436 8 9.107 3×10-11 8.501 1×10-15 0.100 3 7.611 7×10-13 4.440 0×10-15 0 0 100

表 2 计算结果 Table 2 Computational results

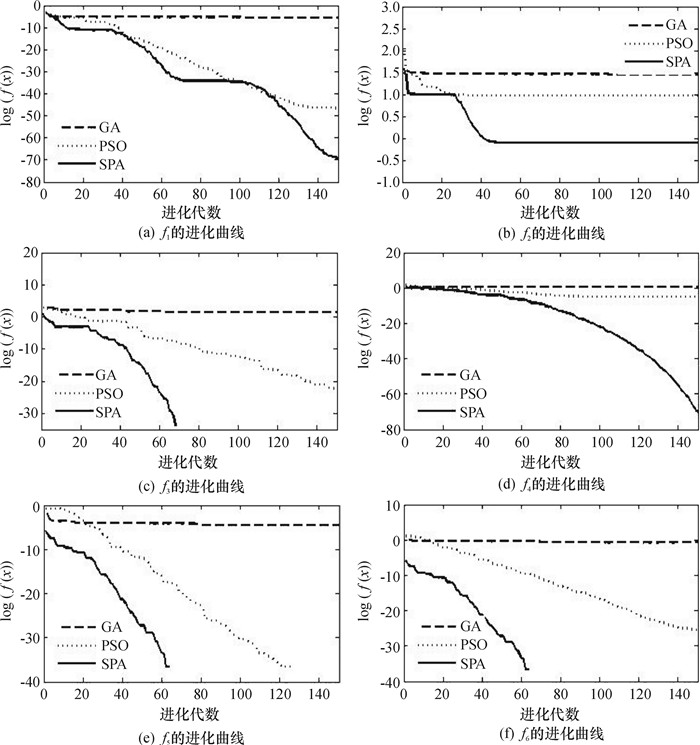
从图 4~图9可知，SPA比GA, PSO有更快的收敛速度，并且有跳出陷入局部最优解的能力；在相同精度下，算法SPA比算法GA, PSO需要的迭代次数更少；图8中，对于f₅，虽然PSO与SPA算法均收敛于最优值，但算法SPA只需要62次迭代，而PSO需要128次迭代.

图 4(Figure 4)

图 4 各函数进化曲线 Figure 4 Convergence curves of all functions

从上实验分析可以看出，与GA, PSO比较，SPA在收敛速度、求解精度、稳定性等方面均显示出其优越性，说明模拟追逐算法是一种有较强寻优能力的群体智能算法.

案例  (选址问题)假设要选定一个供应中心的位置, 为城市中固定的m个用户服务，供应的商品可以是水、电、牛奶或其他货物.求供应中心的位置，使其到各个用户的距离(之和)最小.假设现有10个用户，位置为{(x_i, y_i)|

(2.517 8, 3.246 3), (-2.984 1, 3.307 0), (1.058 9, -3.219 7), (-1.772 0, 0.375 1), (3.660 1, 3.719 1), (-2.739 1, 3.764 7),

(3.657 3, -0.117 0), (2.402 2, -2.864 9), (-0.625 9, 3.325 9), (2.337 7, 3.675 9)}.

解  假设供应中心的位置C=(x，y), 建立优化问题模型.

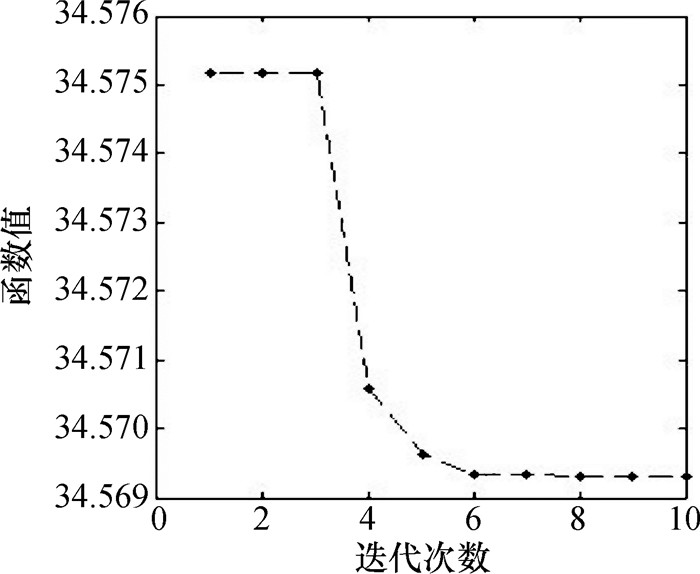
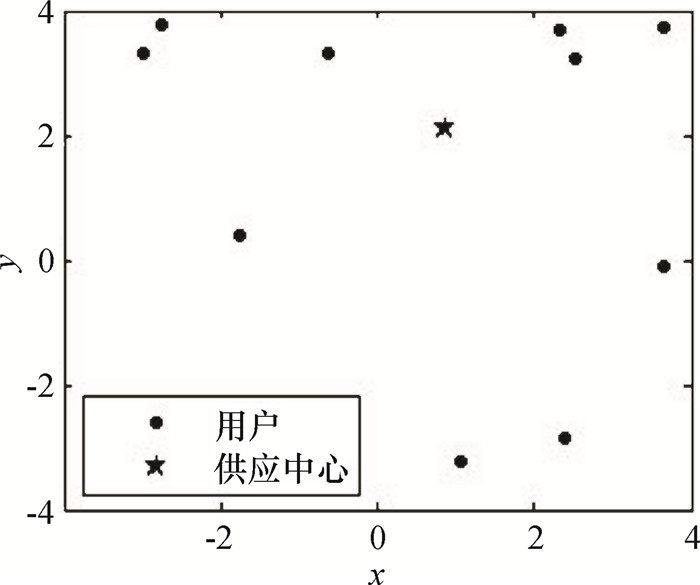
采用Matlab给出选址问题的精确最优解为(0.877 1，2.117 1)，最优值为34.569 3.为使用模拟追逐算法求解，设置控制参数：T_Max=10，N=10, r=0.5, m=5，G₀=50, α=80.算法SPA计算出最优解与精确解一致, C^*=(0.877 111 032 786 5，2.117 105 766 708 5), f^*=34.569 318 766 834 06.算法进化曲线如图 5所示，算法所求供应中心位置如图 6所示.

图 5(Figure 5)

图 5 算法进化曲线 Figure 5 Convergence curve of SPA

图 6(Figure 6)

图 6 供应中心位置 Figure 6 Address of provision center

SPA是一种对人类行为进行智能仿生的优化算法.融合了试探性开拓与有目的性的追逐相结合的优点，具有模型简单，优化性能高的优点.实验仿真结果证实了模拟追逐算法的优越性.