在实际生活中，有很多多目标决策问题^[1-3]，而在决策者所给出的多目标之间往往是相互冲突的.所以, 多目标决策往往只能综合考虑所有目标后, 得到一组非劣解(本文常称为Pareto解^[4]).作为当今研究的热点问题, 许多文献^[5-8]都对寻找多目标优化问题Pareto解的方法进行了研究，并且在多领域应用^[9-10].但这些方法所求得的解是整个多目标优化问题的非劣解集，而对于如何挑选解得工作仍交由决策者来做.由决策者在所给出的许多Pareto解集里面，选择自己偏好的解，这需要决策者的一些专业知识以及专家的意见，才能够挑选出满意的解，因而这对于决策者来说是非常困难的.所以在有的多目标优化问题中，人们往往只对与他们偏好有关的Pareto解感兴趣.

近些年来，决策者在解决多目标优化问题的时候，加入个人的偏好，成为了一个热点话题.一般所加入的偏好方式有多种，比如，有的决策者偏好目标函数的部分区域，有的偏好一个点，有的会给出一个参考方向，而有的会给出目标函数的重要性等等^[11-16].决策者不同，所加入的个人偏好也会不相同.本文将提出一种新的偏好方式，在Delphi^[17]法下，决策者对目标函数的重要性进行打分，然后分析这些打分，得到目标函数的权重范围；再经过本人提出的处理分值的方法，不仅能够求得目标函数的多组权重，得到多目标问题的偏好解，而且还能够具体地反映出决策者的偏好解与权重范围的集中程度的关系，从而更方便决策者挑选偏好解.

多目标优化问题的模型

其中，x是决策变量，f(x)是目标向量且各个目标可以是冲突的，x是Rⁿ中的超矩形域，表示决策空间.

Delphi是群决策中的一种交互式方法，采用背对背的通信方式征询专家小组成员的预测意见，经过几轮征询，使专家小组的预测意见趋于集中，最后做出符合市场未来发展趋势的预测结论.Delphi法使用时第一轮成员的反应常常是非常分散的，在以后的各轮，通过信息反馈和交互，群的反应即种群中多个成员反应的平均值将愈来愈集中.引入Delphi法来处理多目标优化问题的优点是专家对目标函数的重要性打分具有一定的代表性、真实性、合理性.经过三四轮的打分，目标函数的重要性分值就会趋于稳定，而且相对比较集中，那么得到的最后的结果就是相对比较稳定的目标函数的权重范围.

对多目标问题，多决策者根据自己对目标函数的分析，对每个目标函数进行打分过程如下：设有k个决策者参与打分，k≥l.每一个决策者都要对这m个目标打分，以100分为标准，每个决策者对m个目标打分的总和为100分，分值的大小代表重要性的大小.由于Delphi法的特点，本文只取最后一轮的结果.设最后一轮中，第i个决策者对第j个目标函数的打分为S_ij，i=1, 2, …, k; j=1, 2, …, m, 且有$\sum\limits_{j = 1}^m {{S_{ij}} = 100} $，对任意的i都成立.S_ij表示第j个目标函数在第i个决策者心目中的重要性.

因为每个决策者对每个目标函数都打了分，那么可以找出每个目标函数在k个决策者打分下的分值区间.S_ij，i=1, 2, …, k，是k个决策者对第j个目标函数的打分，且记S_xj=min {S_1j, S_2j, …, S_kj}，S_dj={max S_1j, S_2j, …, S_kj}，j=1, 2, …, m.则第j个目标函数的分值区间记为D_j= [S_xj, S_dj]，j=1, 2, …, m.设第j个目标函数每个小区间的长度记为d_j，${d_j} = \frac{{{S_{dj}} - {S_{xj}}}}{k} $, j=1, 2, ...m，那么这k个区间为

把决策者的打分根据分值的大小，对号入座到每个小区间中，对于目标函数f_j的一个区间Q_ij，i=1, 2, …, k.如果有a个决策者的打分在此区间内，那么本文可记区间Q_ij的概率为$ \frac{a}{k}$，这样f_j的k个小区间每一个都会有一个概率，记为p_ij，(0≤p_ij≤1)，i=1, 2, …, k，j=1, 2, …, m，表示第j个目标函数第i个区间的概率，且p_ij满足：p_1j+p_2j+…+p_kj=1，j=1, 2, …, m.

对每个目标函数的区间概率，都对应一个轮盘，以目标函数f_j为例，j=1, 2, …, m，把这个轮盘分为k份，然后在转盘上，标上刻度，从S_xj开始，按顺序根据每个区间所占的比例在转盘上标出刻度，区间概率为0的不用标出，直到标到最后一个，这样就把决策者们对目标函数的偏好表现在转盘上.决策者对每个目标函数的的偏好，已体现在转盘上，每个目标函数对应一个转盘，这样就得到m个转盘，每个转盘上都有刻度，然后对m个转盘转一次，就会得到m个数字，把这些数字记为W_tj，t=1, 2, …，j=1, 2, …, m，表示第t次第j个目标函数转得的数字，记累积概率为P_1j=P_1j, P_2j=p_1j+p_2j, …, P_kj=p_1j+p_2j+…p_kj.然后计算对目标函数j第t次所转的角度θ_tj，则判断θ_tj与P_ij的大小关系，若P_i′j≤θ_tj≤P_ij(i′＜i), 可以就记θ_tj属于区间Q_ij，那么所得的权重为, ${W_{tj}} = \left[{{S_{xj}} + \left( {i-1} \right){d_j} + \frac{{{\theta _{tj}}-{{360}^ \circ }{P_{i-1, j}}}}{{{p_{ij}}}}{d_j}} \right]/100 $，其中S_xj表示第j个目标函数的最低打分，d_j表示第j个目标函数的小区间长度，j=1, 2, …, m, 然后求得第t次转转盘得到的目标函数的权重为w_t=(w_t1, w_t2, …, w_tm)，w_tj，t=1, 2, …，j=1, 2, …, m表示第t次得到的目标函数的权重，其中$\frac{{{W_{tj}}}}{{\sum\limits_{j = 1}^m {{W_{tj}}} }} $表示第t次得到的目标函数j的权重.

这样就确定了目标函数的权重，然后再采用M2M^[18]的方法进行优化求解.

问题1

问题2

问题3

首先测试的3个问题，前两个是有2个目标函数优化问题，第3个是3个目标函数的优化问题，那么可以采用基于Pareto方法的M2M算法进行计算，求出问题的非支配解集和Pareto曲线，然后采用本文所提出的方法进行偏好分析，最后得到具体的权重.首先对3个问题进行计算:种群规模为100，进化代数为10 000，交叉率为0.7，变异率为0.01.

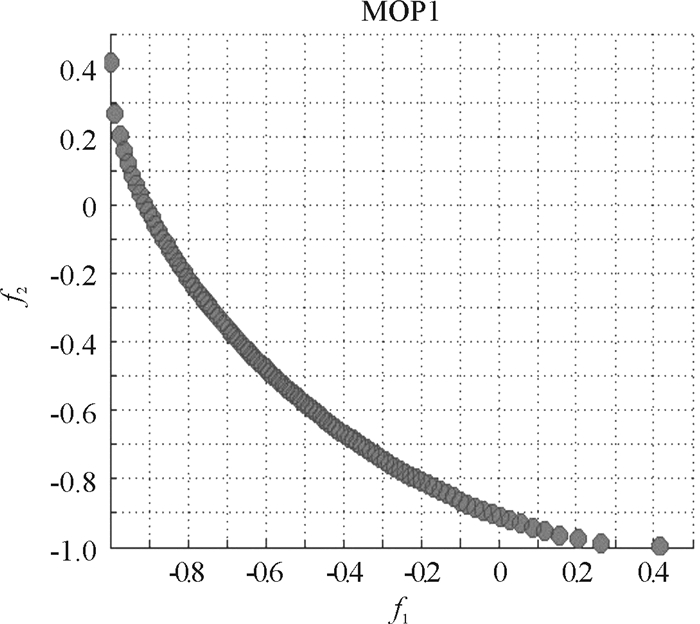
问题1、2、3的无偏好Pareto曲线图分别见图 1、图 2、图 3.

图 1(Figure 1)

图 1 问题1无偏好Pareto解 Figure 1 Pareto solution to Problem 1 with no preference

图 2(Figure 2)

图 2 问题2无偏好Pareto解 Figure 2 Pareto solution to Problem 2 with no preference

图 3(Figure 3)

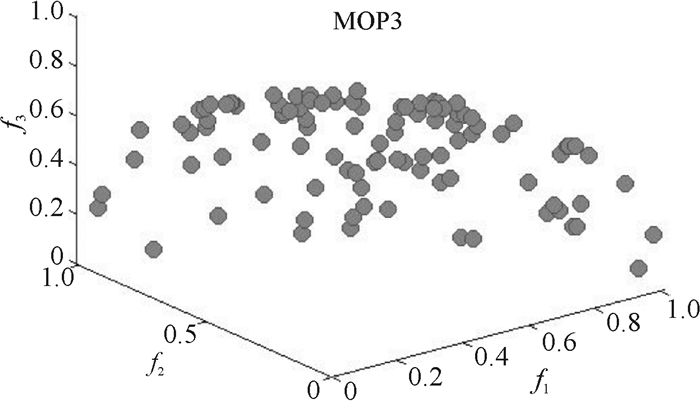
图 3 问题3无偏好Pareto解 Figure 3 Pareto solution to Problem 3 with no preference

采用Delphi法进行打分，假设10个专家对这3个问题的各个目标函数的重要性打分如表 1、表 2所示.(令问题1和2的两个目标函数的打分一样的情况)

表 1(Table 1)

表 1 专家对问题1、2的打分(偏好1) Table 1 Experts' scores of Questions 1 and 2(Preference 1) 专家 目标函数f1 目标函数f2 总分 1 70 30 100 2 66 34 100 3 58 42 100 4 65 35 100 5 63 37 100 6 60 40 100 7 59 41 100 8 61 39 100 9 65 35 100 10 67 33 100

表 1 专家对问题1、2的打分(偏好1) Table 1 Experts' scores of Questions 1 and 2(Preference 1)

表 2(Table 2)

表 2 专家对问题3的打分(偏好2) Table 2 Expert's scores of Question 3(Preference 2) 专家 目标函数f1 目标函数f2 目标函数f3 总分 1 32 28 40 100 2 30 25 45 100 3 36 30 34 100 4 33 27 40 100 5 32 26 42 100 6 37 25 38 100 7 34 23 43 100 8 40 28 32 100 9 42 24 34 100 10 37 29 34 100

表 2 专家对问题3的打分(偏好2) Table 2 Expert's scores of Question 3(Preference 2)

首先可以计算出两个目标函数的权重偏好范围，由表 1得到，f₁的打分区间为[58, 70], f₂的打分区间为[30, 42]，所以f₁的权重偏好范围为[0.58, 0.7], f₂的权重偏好范围为[0.3, 0.42].从表 2得到问题3的3个目标函数的权重偏好范围分别为[0.3, 0.42], [0.24, 0.3], [0.32, 0.45].然后采用上面的权重选取方法，求出问题的偏好解.

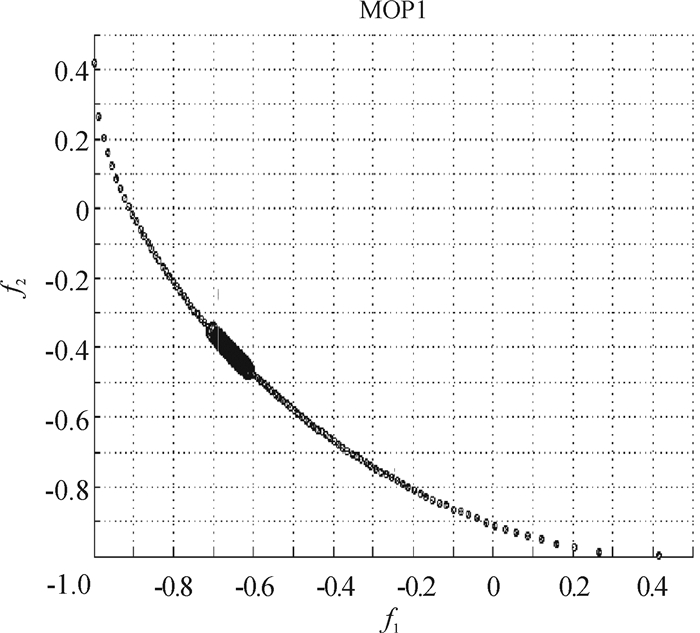
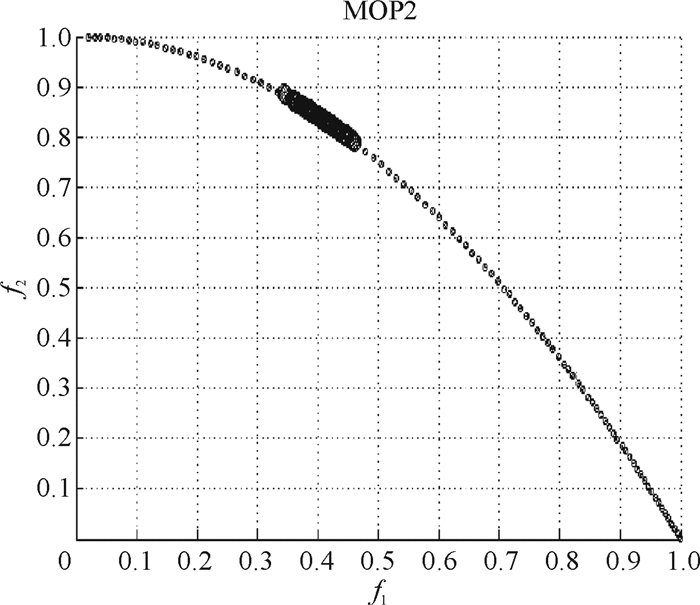
那么这3个问题在这两组打分下的最优解(问题1和问题2的打分一样的情况下)见图 4、图 5、图 6.

图 4(Figure 4)

图 4 问题1偏好Pareto解 Figure 4 Pareto solution to Problem 1 with preference

图 5(Figure 5)

图 5 问题2偏好Pareto解 Figure 5 Pareto solution to Problem 2 with preference

图 6(Figure 6)

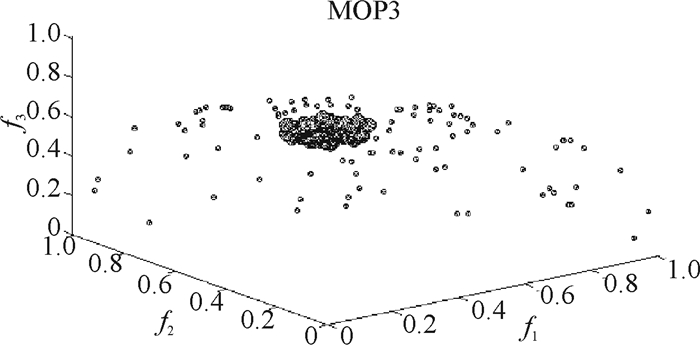
图 6 问题3在偏好2下的Pareto解 Figure 6 Pareto solution to Problem 3 with Preference 2

图中粗线部分表示求得的偏好解，细线部分表示没有偏好的最优解集.

当把问题1、2两个问题目标函数的打分互换一下，就可以得到偏好3，如表 3所示.

表 3(Table 3)

表 3 交换表 1中专家对问题1、2的打分(偏好3) Table 3 Exchange expert's scores of Questions 1 and 2 in Table 1(Preference 3) 专家 目标函数f1 目标函数f2 总分 1 30 70 100 2 34 66 100 3 42 58 100 4 35 65 100 5 37 63 100 6 40 60 100 7 41 59 100 8 39 61 100 9 35 65 100 10 33 67 100

表 3 交换表 1中专家对问题1、2的打分(偏好3) Table 3 Exchange expert's scores of Questions 1 and 2 in Table 1(Preference 3)

此时问题1、2得到的偏好解分别如图 7、图 8所示.

图 7(Figure 7)

图 7 问题1在偏好3下的Pareto解 Figure 7 Pareto solution to Problem 1 with Preference 3

图 8(Figure 8)

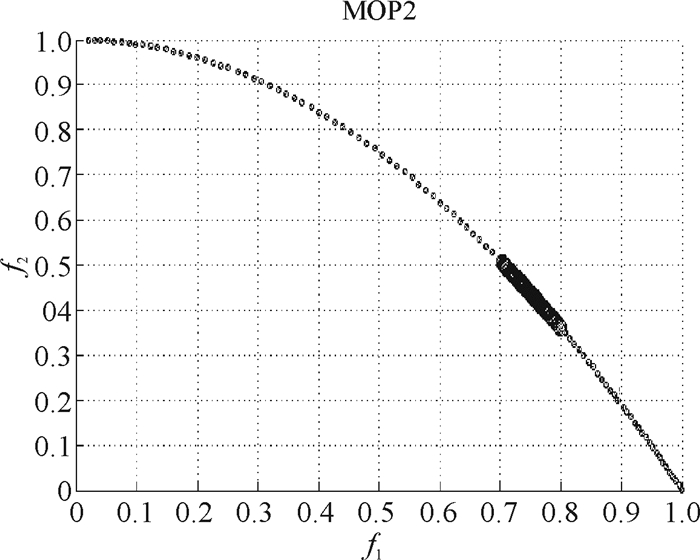
图 8 问题2在偏好3下的Pareto解 Figure 8 Pareto solution to Problem 2 with Preference 3

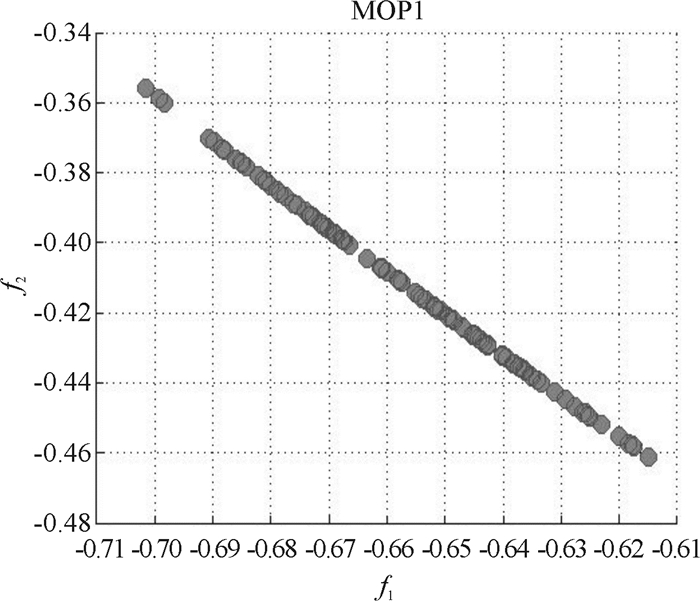
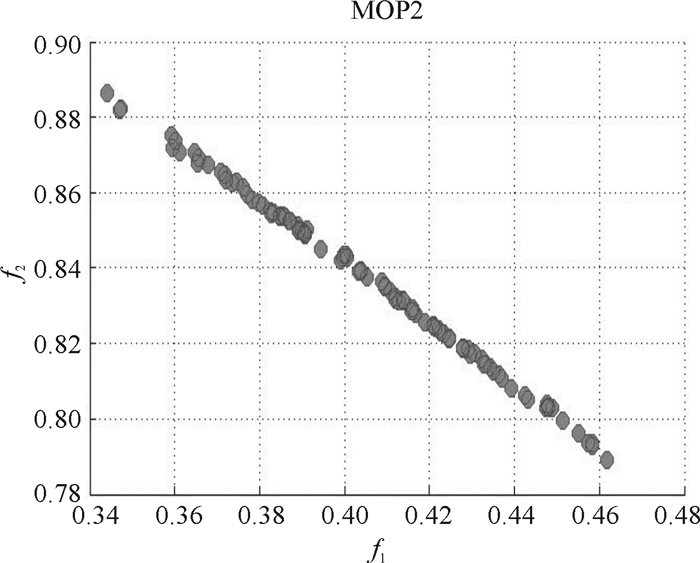
在第3组权重下，放大问题1、问题2所得的偏好图分别如图 9、图 10所示.

图 9(Figure 9)

图 9 问题1在偏好3下解的扩大 Figure 9 Solution amplification of Problem 1 with Preference

图 10(Figure 10)

图 10 问题2在偏好3下解的扩大 Figure 10 Solution amplification of Problem 2 with Preference 3

从所得到的图 4~8中可以看到，所求出的偏好解是最优解的一部分，而且对目标函数是二维的问题很容易看出，在第1组偏好下所求得的解是偏向f₂的，因为由偏好权重看出，目标函数f₂要比f₁重要.在第2组交换打分后的偏好下所求得的解是偏向f₁的，因为由偏好权重看出，目标函数f₁要比f₂重要.

在所得到的只有偏好解的图形9、图 10中可以看出，偏好解是有一部分集中、一部分分散的，这与决策者的打分完全一致的，如果决策者的打分很平均，那么得到的偏好解也很平均.所以此种处理打分的方法能够很好地体现决策者的偏好，具有一定的现实意义.

首先介绍了处理偏好权重的方法，然后通过实例计算得到了期望的结果.结果证明了这种方法在处理权重上是十分有效的.这种方法不用对优化算法进行修改，只是利用原有的优化方法来进行计算，这种处理偏好的方法易于理解和使用；对于任意维的多目标都可以求出偏好权重，需要做的是对于原有的解决多目标优化权重算法的改进，从而更好地结合此种方法，获得更好的偏好解.