聚类分析是数据挖掘中主要任务之一,也是数据挖掘领域中研究的重要课题,它能够根据数据特性将数据库中具有相似特性的数据分类到相同的类或者簇中,使同一个类或者簇具有相似性,不同的类或簇具有很大的相异性[1-2].根据聚类分析所使用的方法类型来划分有:基于图论的聚类方法、基于划分的聚类方法、基于层次的聚类方法、基于网格的聚类方法、基于密度的聚类方法等[3-5].
DBSCAN算法(Density-Based Spatial Clustering of Applications with Noise, 具有噪声的基于密度的聚类方法)是一种基于密度的聚类算法[6],该算法利用全局Eps半径和最低密度阈值MinPts过滤低密度的区域,将稠密样本点归类到一个聚类簇中,与其他聚类算法一样具有聚类快、可过滤噪声点和发现任意形状的聚类的优点,但是DBSCAN算法在对大规模数据进行聚类时,时间激增、内存支持和I/O消耗增加,同时数据分布差异巨大导致聚类精度下降.
针对上述问题,周水庚等人在文献[7]中提出了数据分区的DBSCAN算法,减少了算法内存需要,为并行DBSCAN算法奠定了基础.随着高性能计算机的出现,何中胜等[8]提出建立在集群式高性能计算机上的并行PDBSCAN算法,提高算法并行性、降低了算法对时间和空间的需要,PDBSCAN算法I/O消耗仍然较大;宋明等[9]提出基于数据交叠分区的并行OPDBSCAN算法,提高聚类的并行性、减少局部聚类合并时的通信量,但OPDBSCAN算法采用了和DBSCAN算法一样的全局Eps参数,当数据分布不均匀的时,聚类精度较差.随着云计算技术的发展,郗洋在文献[10]提出了HDBSCAN算法,将HDBSCAN算法与MapReduce编程模型结合,一定程度上解决了内存和I/O消耗激增问题.本文结合数据重叠分区思想和云计算平台高效并行的优势提出一种改进的基于数据分区预处理的MapReduce化的PMDBSCAN算法,提高聚类的效率和精度、减少内存需要和I/O消耗.
1 基于密度的DBSCAN算法 1.1 DBSCAN算法DBSCAN算法核心思想是:对于数据库中构成类或者簇的任何一个对象,在一个给定半径(表示为Eps)的邻域内所包含的对象的个数,必须不小于一个全局的阈值MinPts[6].下面介绍一些DBSCAN算法相关概念.
(1) Eps-邻域.一个对象设定半径Eps之内的区域就称为这个对象的Eps-邻域.
(2) 核心对象.如果一个对象p在规定的Eps邻域内的对象数大于或者等于给定的MinPts值,那么对象p就是一个核心对象(Core Object).
(3) 边界对象.属于数据库中的对象q在核心对象p的Eps-邻域内,但对象q本身不是核心对象,则对象q是一个边界对象.
(4) 直接密度可达.对于给定的Eps和MinPts值,如果对象q在对象p的邻域内部,并且p是一个核心对象,则对象p和对象q是直接密度可达的.
(5) 密度可达.在数据库中有对象串p1, p2, …,pi, pi+1, pn,对于给定的Eps邻域、MinPts值,如果有任一pi+1都是从pi直接可达的,那么对象串中的任一对象pn对与对象p1都是密度可达的.
(6) 密度相连.对于对象p和对象q,存在一个对象o对于p和q都是密度可达的,那么称p和q密度相连.
(7) 噪声.数据库中不属于任何一个簇类的对象称之为噪声.
在给定的数据集D中随机选择一个对象p,如果p关于Eps邻域密度可达的对象数目大于等于设置的阈值MinPts,那么p就是核心对象,建立新的簇C,将p和所包含的对象均加上簇C的标记.如果p不满足核心对象的要求,暂时将p标记为噪声,算法将继续处理数据库D中下一个没有簇标记的对象,若噪声对象属于其他簇类,则标记为边界对象.重复以上过程直到数据库D中所有的对象都被处理[6].
DBSCAN算法在聚类之前需要确定一个全局的参数Eps, 确定Eps参数的过程需要查询数据库中所有对象在区域中的分布状况.这通常是通过建立R*-树[11],反复查询数据对象的所有密度可达的数据对象,计算与离其最近的MinPts个对象的距离,将距离进行排序生成k-dist图来实现的.在k-dist图中,数据对象和它的第MinPts个数据对象之间的距离用横坐标表示,对应某一k-dist值的对象的个数则用纵坐标来表示[7].
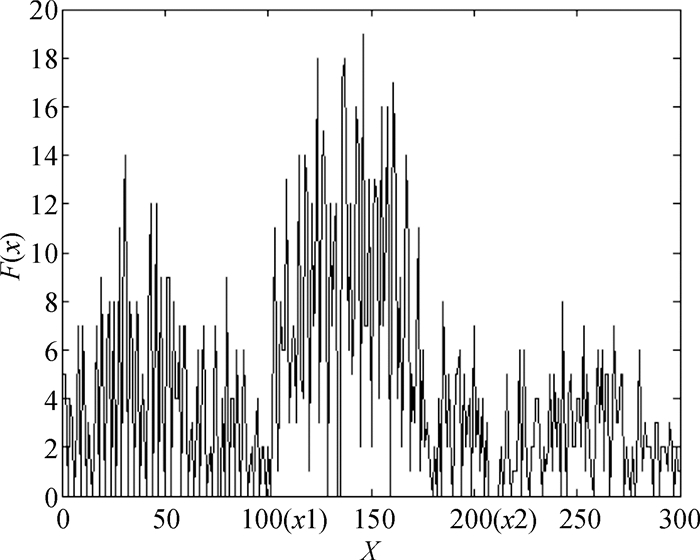
在DBSCAN算法中Eps值对聚类的质量影响非常大,目前对于Eps值的确立没有一个确认有效的方法,在如图 1所示的数据分布特性极度不规则的情况下,更是很难确定一个适合的Eps值.建立R*-树和绘制k-dist图都需要花费大量的时间[12],在对大规模数据库进行聚类时,时间代价急剧增长,而且同时伴随着大量内存支持和I/O的消耗.

|
图 1 分布不均匀数据分布图 Figure 1 Uneven data distribution |
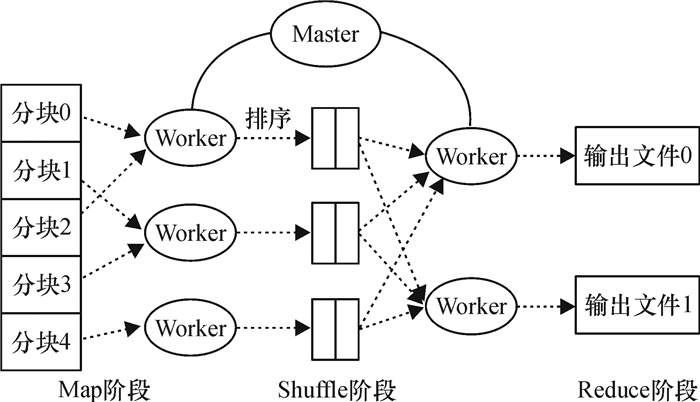
MapReduce是一种由Google提出的用于大规模数据集并行运算的编程模型[13].它可以有效地屏蔽并行运算的底层实现细节,提高并行编程的效率.并且实现MapReduce并行计算利用廉价的商用计算机集群即可.它被广泛地应用在分布排序、分布grep、web连接图反转、数据挖掘等应用程序中.主要运算过程:用户根据需要自定义map函数来处理key/value对[14],产生中间key/value对,经过shuffle阶段,用户再指定reduce函数来处理key/value对,合并具有相同key的中间value对产生最终0或者1个输出.MapReduce算法的运行流程如图 2所示.
|
图 2 MapReduce算法流程图 Figure 2 Flowchart of MapReduce algorithm |
Hadoop平台的核心组件包括分布式编程模型引擎Hadoop MapReduce(Google MapReduce)、分布式文件系统HDFS(Google File System的开源版本)[15].Hadoop是一个开源的云计算框架,利用它可以实现在集群计算机上使用简单的的编程模型来编写和运行并行的分布式应用程序来处理大规模数据.
2 基于数据分区预处理的MapReduce化的DBSCAN算法(PMDBSCAN)PMDBSAN算法的步骤:将数据集分为没有交集的几部分,求出分区的Eps邻域值, 将分区数据和分区的Eps值及全局Minpts阈值输入Hadoop平台,进行并行计算.根据集群各个节点的内存和计算资源情况将分区进一步切片,切片时结合数据重叠区理论利于提高局部聚类合并质量[9],减少I/O消耗,对二次分区的数据局部聚类、合并局部聚类,最后将分区的聚类合并得到最终的聚类结果.算法的步骤如图 3所示.

|
图 3 PMDBSCAN算法步骤图 Figure 3 PMDBSCAN algorithm procedures |
DBSCAN算法进行聚类过程中,并没有要求所有的聚类是均匀的,全局邻域Eps只是一个形成聚类需要满足的最低阈值[6].PMDBSCAN根据数据分布特征对数据库进行分区预处理,针对分区设定不同的Eps值,在满足数据库聚类的最低阈值的同时提高聚类的精细度,这样做是合理有效的.如图 4所示,本文根据图 1数据集在一维上的分布特性进行预分区处理:采取随机抽样方法对数据库进行一次遍历,得出数据库在一维上的投影,然后根据数据在一维上的分布特征(其他维度平均分割)将数据分割为3个分区,对分区数据构建R*-树,画出k-dist图,求出局部的Eps值.
|
图 4 数据集在X维度分布特征图 Figure 4 Sets of data distribution in X dimension |
数据库进行分区后得到D1,D2,Di…, Dn,分区Di数据分布相对均匀,对分区Di进行切片时必须考虑到分区的分割线附近的数据对象.为了最大限度地减少分区对聚类结果的影响,文献[9]将分割线附近的数据对象划分到相邻的两个数据分区中.在分区之间建立重叠带,每个类邻域内的数据对象全部都包含在了同一个数据分区之内,在进行局部聚类合并时只需要处理边界对象集,而不用发送边界附近的所有对象信息到相邻的数据分区,这样提高聚类质量的同时减少通信量、降低I/O消耗.
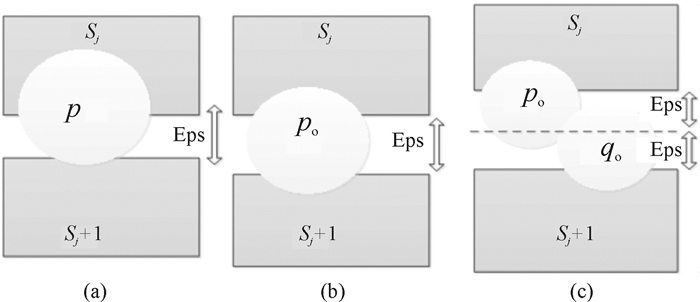
重叠带大小的设置的基本原则是分割线附近的对象p和其邻域内的对象尽可能在一个分区之内.设sj是分区Sj和分区Sj+1的分割点(0≤j≤n,n为分区Di切片的个数),由图 5中(a)图可以发现当重叠区宽度小于Eps或者宽度为Eps-2Eps的时候,p邻域内的点可能分布在分区Sj和分区Sj+1中,分区Sj和分Sj+1都无法获得p的邻域全部点的信息,这样重叠带完全失去了意义,所以重叠带的宽度必须大于等于2Eps值,才可以使对象p或者q的邻域信息完全分布在分区Sj或者Sj+1中[9].在重叠比(重叠带数据与分区总数据的比值)小于ц的前提下进行切片划分,在分区数据Di中的重叠带有[s1-Eps,s1+Eps],[s2-Eps,s2+Eps],[sj-Eps,sj+Eps],与切片结合起来,Di的最后n个数据分区为[s0,s1+Eps],[s1-Eps,s2+Eps],[sj-Eps,sj+1+Eps],[sn-2-Eps,sn-1],为方便表达第j个数据分区表示为SCj(j=1, 2, …, n-2).
|
图 5 分区重叠带示意图 Figure 5 Schematic partitions in overlapping zone |
数据经过第二次切分之后已经满足可以在单个节点进行聚类运算,根据分区Di的邻域半径Epsi,全局密度阈值MinPts进行DBSCAN聚类运算,得到局部的聚类结果之后需要对局部的聚类进行合并,聚类合并有两个步骤:
(1) 分区SC1, …, SCj, …SCn的局部聚类的合并.重叠带区域的任一数据对象p都进行了两次数据聚类,聚类的合并需要依据两次聚类的信息.p在两个相邻重叠分区分别属于簇类A和簇类B,如果p属于类A或者类B的核心对象,或者在两个类中均是核心对象,则类A和类B合并为一个聚类;如果p在两个类中均属于边界点,那么不能确定类A和类B合并,p可以划分至两个聚类中的任意一个;如果p属于其中一个类,在另一次聚类中被划分为噪声点,则p属于其所在的聚类;如果在两次聚类中p均被划分为噪声点,则在整个Di分区中p属于噪声点.
(2) 分区D1, D2, ..Di…, Dn聚类的合并.经过步骤1数据分区Di内部的聚类已经完成,由于分区Di和Di+1之间没有重叠分区,两个分区边界的对象无法通过相同的数据对象来判断是否形成聚类,只能通过边界局部类的信息(核心对象、代表点、边界位置等)以近似条件来进行聚类.其聚类合并分为3种情况:
① 类CA与类CB分别在Di与Di+1中,需要合并类的条件:Di和Di+1的Eps值分别是Epsi和Epsi+1,Epsmin=min(Epsi,Epsi+1),EA和EB是在步骤(1) 中保存的边界对象集,Dist{p, q}(∀p∈EA,∀q∈EB)是两个对象集中任一对象的距离,满足条件(1)
| $ \overline {{\rm{dist1}}} {\rm{ = }}\frac{{\sum\nolimits_\mathit{i}^{} {\sum\nolimits_\mathit{j}^{} {{\rm{Dist}}\left\{ {{\mathit{p}_\mathit{i}}{\rm{, }}{\mathit{q}_\mathit{j}}} \right\}} } }}{{|{\mathit{E}_\mathit{A}}|*|{\mathit{E}_\mathit{B}}|}} \le {\rm{Ep}}{{\rm{s}}_{{\rm{min}}}} $ | (1) |
来达到与DBSCAN类似的聚类效果.
② 噪声点归并到类:Di边界附近的噪声点有可能是总体聚类中某个类的边界点,若点p是Di边界的噪声点,类C是Di+1中边界附近的类,邻域半径为Epsi+1, Ec是类C保存的边界点域集(∀q∈Ec), 当式(2) 满足时将噪声点p归并到类C中.
| $ \overline {{\rm{dist2}}} {\rm{ = }}\frac{{\sum\nolimits_\mathit{j}^{} {{\rm{Dist}}\left\{ {\mathit{p}{\rm{, }}{\mathit{q}_\mathit{j}}} \right\}} }}{{|{\mathit{E}_\mathit{c}}|}} \le {\rm{Ep}}{{\rm{s}}_{\mathit{i}{\rm{ + 1}}}} $ | (2) |
③ 合并噪声点形成新类:虽然预处理划分数据的依据是数据分布特征,仍然存在把同一个较稀疏的聚类划分至不同分区形成噪声点的可能.设EA、EB是相邻两个分区的边界对象集,Epsmin= min(EpsA,EpsB),其噪声的集合为S,∃p∈S,若在S中在p的Epsmin半径内存在超过MinPts个对象,则将噪声集合建立以p为核心点的簇类.
2.4 PMDBSCAN算法伪代码PMDBSCAN Procedure(DataBase db)
procedure-prePartitiondb(db) //对数据库进行预分区, 得到分区Di(i=1, 2, …,n)
foreach Di of db do
rkpart(Di)//对每个分区计算Epsi
end foreach rkpart//将分区Di和其Epsi和阈值MinPts输入到Hadoop平台中进行二次分区、局部聚类和聚类的合并
foreach input Hadoop to MapReduce(Di,Epsi,MinPts)
MapReduce sec-Partition(Di, Epsi)//对分区Di进行分割
part dbcluster(SCj, Epsi, MinPts)//对重叠分区SCj局部DBSCAN聚类
MapReduce mergeCluster()//局部聚类进行合并
end MapReduce
end PMDBSCAN Procedure
procedure MapReduce sec-Partition()
Map:input(key, value)//行递进向量,value为数据点向量+是否边界点
output(key, value)//切片数据以文件名fname为key保存到节点,value为数据点向量+是否重叠带+是否为边界点
foreach (p) do
if (distance of p to division line < Epsi)
tagp=1
else边界信息置为0
if(p in overlap zone)//p位于重叠带标识置为1
output(p to fname_j and fname_j+1)
else output (p to fname_j)//同时将p的重叠带标识置为0
end foreach
Reduce:input(key, value); //key:fname,value:数据点向量+是否边界点+是否重叠带点
output null;
foreach(value) output(value) to fname; //相同fname的点归结到一个文件内
end MapReduce sec-Partition()
procedure MapReduce mergeCluster()
Map input:(key, value)//key:簇标示, value;数据点向量+边界Tb+是否重叠带点To
output:边界点p,簇标示+是否核心点
if (Tb is 0 or To is 0) output (p所属簇标示, 是否核心点)to Redecue
else output(p所属聚类代表) to outputfile//输出到最终聚类结果
Reduce input:(key, value)//key:边界点或重叠带点p, value:簇标示id,是否核心点
output:(key, value)//边界点或重叠点p,value:合并的聚类代表+是否合并
foreach(value)
if(p is core object)
if(To is 0) output cluster merge//类合并
else p merge q or not //按2.3规则合并
else p merge to q //p归并到q代表的类
or p and other point merge to new cluster
or output to noise
end foreach
end procedure MapReduce mergeCluster()
3 实验结果与性能评价算法的仿真实验在具有9个节点的计算机集群上实现.集群节点采用联想ThinkCentre M8400t商用台式机,它具有四核心八线程的的英特尔酷睿i7 3770CPU、4 GB内存和一个SATA2 7 200转每秒、容量为1 TB的硬盘,操作系统使用ubuntu12.10,所有的节点由千兆以太网交换机相连,云计算平台使用分布式开源平台Hadoop 1.2.0版本.
为了测试PMDBSCAND聚类算法在聚类质量方面改进的特点,首先对如图 1的模拟数据集分别进行DBSCAN算法和先进行划分3个分区预处理的PMDBSCAN算法(参考图 2).由表 1、表 2的实验结果可以发现PMDBSCAN算法采取划分分区再确定分区Eps值的处理,其聚类思想比较合理,得到的聚类结果更加接近正确的聚类分布.
| 表 1 DBSCAN聚类质量测试结果 Table 1 DBSCAN clustering test results |
| 表 2 PMDBSCAN聚类测试结果 Table 2 PMDBSCAN clustering test result |
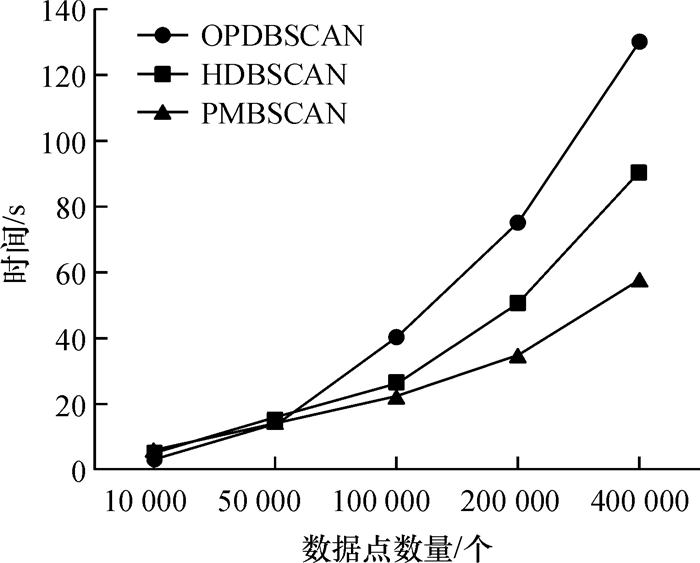
图 6是OPDBSCAN算法、HDBSCAN算法和PMDBSCAN算法对大规模数据进行聚类的时效图.实验需要数据利用用聚类测试数据生成算法clugen.c [16]生成,在数据点个数为10 000、50 000、100 000、200 000、400 000的情况下算法时间性能图.由时效图可以发现对大规模数据聚类时PMDBSCAN算法比OPDBSCAN算法和HDBSCAN算法具有更快的聚类的速度.当数据规模不断地增大时,PMDBSCAN算法增长幅度较小,扩展性更好.
|
图 6 算法聚类时间比较图 Figure 6 Comparison of cluster algorithm execution time |
在PMDBSCAN算法中,每个节点只需要与相邻的节点交换重叠区对象的部分信息,重叠分区数据与数据的总量比小于ц值,当节点数目达到一个数后,I/O消耗趋于稳定[9],这样I/O消耗得到了有效的控制.
4 结论实验结果表明,在各分区采用不同Eps值改善了聚类的精度,在利用Hadoop平台达到算法MapReduce并行化过程中采取重叠分区的数据分割策略提高算法的并行性、提高算法效率、降低I/O消耗并且使局部聚类合并的结果更加精确.
PMDBSCAN算法由于在预分区处理过程中采用基于取样和统计的分区方法,局部聚类采用DBSCAN,这些过程存在自动化程度低、效率较低问题.研究如何实现数据的高效率自动划分,在局部数据聚类采用快速DBSCAN算法提高局部聚类速度是下一阶段的主要研究工作.本文目前只实现了大规模(二维空间)静态数据集的DBSCAN聚类并行化,对高维度空间数据集和动态增长数据集的并行化聚类有待研究.
| [1] | CHEN M, HAN J, YU P S. Data mining:an overview from a database perspective[J]. IEEE Transactions on Knowledge and Data Engineering, 1996, 8(6): 866-883. DOI: 10.1109/69.553155. |
| [2] |
刘宏伟, 石雅强, 梁周扬, 等. 面向聚类挖掘的局部旋转扰动隐私保护算法[J].
广东工业大学学报, 2012, 29(3): 28-45.
LIU H W, SHI Y Q, LIANG Z Y, et al. Partial rotation p erturbation for privacy-preserving clustering min ing[J]. Journal of Guangdong University of Technology, 2012, 29(3): 28-45. |
| [3] | XU R, WUNSCH D. Survey of clustering algorithms[J]. IEEE Transaction on Neural Networks, 2005, 16(3): 645-678. DOI: 10.1109/TNN.2005.845141. |
| [4] |
孙吉贵, 刘杰. 聚类算法研究[J].
软件学报, 2008, 19(1): 48-61.
SUN J G, LIU J. Clustering algorithms research[J]. Journal of Software, 2008, 19(1): 48-61. |
| [5] |
贺玲, 吴玲达, 蔡益朝. 数据挖掘中的聚类算法综述[J].
计算机应用研究, 2007, 24(1): 10-13.
HE L, WU L D, CAI Y C. Survey of clustering algorithms in data mining[J]. Application Research of Computer, 2007, 24(1): 10-13. |
| [6] | ESTER M, KRIEGEL H, JÖRG S. A densith-based algorithm for discovering clusters in large spatial databases with noise[C]// Proceedings of International Conference on Knowledge Discovery & Data Mining.Portland:AAAI, 1996:226-231. |
| [7] |
周水庚, 周傲英, 曹晶. 基于数据分区的DBSCAN算法[J].
计算机研究与发展, 2000, 37(10): 1153-1159.
ZHOU S G, ZHOU A Y, CAO J. A data-partitioning-based DBSCAN algorithm[J]. Journal of Computer Research and Development, 2000, 37(10): 1153-1159. |
| [8] |
何中胜, 刘宗田, 庄燕滨. 基于数据分区的并行DBSCAN算法[J].
小型微型计算机系统, 2006, 27(1): 114-116.
HE Z S, LIU Z T, ZHUANG Y B. Data-partitioning-based parellel DBSCAN algorithm[J]. Journal of Chinese Computer Systems, 2006, 27(1): 114-116. |
| [9] |
宋明, 刘宗田. 基于数据交叠分区的并行DBSCAN算法[J].
计算机应用研究, 2007, 21(7): 17-20.
SONG M, LIU Z T. A data-overlap-partitioning-based parallel DBSCAN algorithm[J]. Application Research of Computers, 2007, 21(7): 17-20. |
| [10] | 郗洋. 基于云计算的并行聚类算法研究[D]. 南京: 南京邮电大学计算机学院, 2012. |
| [11] | BECKMANN N, KRIEGEL H, SCHNEIDER R, et al. The R^*-tree : an efficient and robust access method for points and rectangles[J]. International Conference on Management of Data, 1990, 19(2): 322-331. |
| [12] |
段仰广, 韦玉科. 一种基于排序FP-TREE挖掘最大频繁模式的高效算法[J].
广东工业大学学报, 2009, 26(2): 64-69.
DUAN Y G, WEI Y K. An efficient algorithm for mining maximal frequent patterns based on sorted FP-TREE[J]. Journal of Guangdong University of Technology, 2009, 26(2): 64-69. |
| [13] | DEAN J, GHEMAWAT S. MapReduce:simplified data processing on large clusters[J]. Communications of the ACM, 2008, 51(1): 107-113. DOI: 10.1145/1327452. |
| [14] |
李成华, 张新访, 金海. MapReduce:新型的分布并行计算编程模型[J].
计算机工程与科学, 2011, 33(3): 129-134.
LI C H, ZHANG X F, JIN H. MapReduce: a new programming model for Distributed parallel computing[J]. Computer Engineering and Science, 2011, 33(3): 129-134. |
| [15] | GHEMAWAT S, GOBIOFF H, LEUNG S. The google file system[C]// Proceedings of the Acm Sigmetrics International Conference on Measurement & Modeling of Computer Systems Acm. Bolton Landing, NY, USA:2003:29-43. |
| [16] | MILLIGAN G W. A monte carlo study of thirty internal criterion measuresfor cluster analysis[J]. Psychometrika, 1981, 46(2): 187-199. DOI: 10.1007/BF02293899. |
 2016, Vol. 33
2016, Vol. 33