工程复杂矛盾问题的信息元表示

引用本文

赵锐, 余永权. 工程复杂矛盾问题的信息元表示[J]. 广东工业大学学报, 2016, 33(1): 17-21. DOI: 10.3969/j.issn.1007-7162.2016.01.003.

Zhao Rui, Yu Yong-quan. Information Unit Expression of Complex Engineering Contradiction[J]. Journal of Guangdong University of Technology, 2016, 33(1): 17-21. DOI: 10.3969/j.issn.1007-7162.2016.01.003. 复制到剪切板

基金项目:

国家自然科学基金资助项目(61142012);广东省科技计划项目(2013B090600028)

作者简介:

赵锐(1976-), 女，讲师，博士，主要研究方向为计算智能、智能信息处理、可拓工程等。

文章历史

收稿日期：2015-10-28

Contents Abstract Full text Figures/Tables PDF

工程复杂矛盾问题的信息元表示

赵锐, 余永权

广东工业大学计算机学院，广东广州 510006

收稿日期：2015-10-28

基金项目：国家自然科学基金资助项目(61142012);广东省科技计划项目(2013B090600028)

作者简介：赵锐(1976-), 女，讲师，博士，主要研究方向为计算智能、智能信息处理、可拓工程等。

摘要: 处理工程矛盾问题时，经常会遇到复杂矛盾.但由于目前还没有对复杂矛盾问题的定义及形式化描述进行过研究，所以无法对其进行智能化处理.为解决此问题，定义了复杂矛盾以及矛盾信息元和矛盾信息元集等反映其本质和内涵的一些重要概念，并给出了复杂矛盾问题的信息元表示的方法和步骤.这些成果为工程矛盾问题智能化处理中复杂矛盾问题的分析和解决提供了理论依据.

关键词: 矛盾问题复杂矛盾信息元

Information Unit Expression of Complex Engineering Contradiction

Zhao Rui, Yu Yong-quan

School of Computers, Guangdong University of Technology, Guangzhou 510006, China

Abstract: Complex contradiction often occurs in handling engineering contradictions. However, its definition and formalized description have not been studied, which make intelligent processing impossible. In order to solve the problem, complex contradiction and some key terms such as contradictory information unit and contradictory information unit set are defined and clarified. Also, the methods and steps expressing information units of complex contradiction are given. The results can provide theoretical basis for the analysis and solution of complex contradiction in intelligent processing on engineering contradiction.

Key words: contradiction complex contradiction information unit

在工程活动中总会遇到各种各样的矛盾问题^[1-4].如：地区经济发展中GDP增长和环境保护的矛盾；城市扩建改建中土地占用和耕地保护的矛盾；地铁施工中的工程质量与工程进度的矛盾、技术措施与工程设备的矛盾、工程需求和工程方法之间的矛盾等等.而且很多矛盾常常是相互影响并交织在一起的，这就形成了工程上的复杂矛盾问题，要解决这些问题，就需要对其进行分析.而要分析就要先给出工程复杂矛盾相关的概念和定义，以及描述复杂矛盾的数学模型，这样在分析中才能定量地对其进行有效处理.

在工程问题上，阿奇舒勒创立的TRIZ理论^[5]对矛盾问题进行了有关的研究.但TRIZ是基于工程创造本质的结构性理论^[6-7]，而且是一种定性的理论，并非数学理论或定量理论, 所以对矛盾问题的一般性求解难以起到根本性的指导作用，特别是采用计算机进行矛盾问题处理时存在很多困难和诸多不足.

Poulin.D等人于1993年对专家系统中推理的矛盾规则及冲突消解问题进行了研究^[8]；Carmaona等人于2002年发表文章讨论了基于模糊模型的自适应控制问题，对模糊推理规则中的矛盾测量问题进行了研究^[9].不过，他们两人所研究的“矛盾”，指的都是知识库中“规则的矛盾”；美国马里兰大学的Perlis.D等人于2006年对大型动态信息环境的检测、分类以及矛盾处理进行了研究^[10]，不过他们探讨的矛盾，实际指的是系统的容错问题.由此可见，国外对工程活动中的特殊矛盾也有过一些关注和研究，但并没有从智能处理的角度对一般性质的矛盾问题展开讨论.

国内，曾韬等人专门针对工程矛盾，在矛盾的形式化、主要矛盾识别、矛盾转化和矛盾化解方案评价方面进行了研究，并提出了相应的解决方法^[11-13].这些开创性的工作为工程矛盾智能化处理的研究奠定了基础，但并没有对工程上的复杂矛盾展开研究.而要实现工程矛盾的智能化处理，就必须要对工程活动中经常会遇到的复杂矛盾问题进行研究和探讨，其中首要解决的问题就是工程复杂矛盾问题的定义和工程复杂矛盾问题的信息元表示.

1 工程复杂矛盾问题的定义

设一个工程系统的现行状态为S₀，期望状态(即目标状态)为S_e，若S₀≠S_e，则称工程系统存在问题.问题就是工程系统现有的状态S₀和期望的状态S_e的差异.有些问题，在现有的条件下是可以得到解决的.还有些问题，在现有的条件下是没办法解决的，这类问题就是矛盾问题.工程活动中遇到的矛盾问题，简称工程矛盾.工程矛盾与一般矛盾最大的区别在于其所对应的工程目标一般是既定不予改变的，所以对其进行分析和处理时就只能从问题的条件入手.

对于工程复杂矛盾问题，很难给出全面精确的定义，但可以从不同角度进行描述.

设在工程活动中有一矛盾问题，它有多个目标D₁, D₂, …, D_n，也有多个条件C₁, C₂, …, C_n，若将其分解为若干个子问题P₁, P₂, …, P_l，这些子问题有的是矛盾问题，有的是相容问题，且它们之间还存在相关关系，这样就形成一个矛盾问题网，称其为复杂矛盾问题，表示为

$ {{P}_{\rm{s}}}=\left( {{D}_{1}}\oplus {{D}_{2}}\oplus \cdots \oplus {{D}_{n}} \right)*\left( {{C}_{1}}\oplus {{C}_{2}}\oplus \cdots \oplus {{C}_{n}} \right), $

(1)

如不做特别说明，后文所述的复杂矛盾问题均指工程复杂矛盾问题.

复杂矛盾问题的复杂性主要体现在以下几个方面：

(1) 矛盾问题个数多：复杂矛盾问题当中往往包含比较多的子矛盾问题；

(2) 结构复杂：复杂矛盾问题中的子矛盾问题之间往往存在比较错综的相关关系，彼此间的相关方向不同，相关程度也存在差异；

(3) 传导矛盾：当解决其中一个矛盾问题时，和它相关的其他问题会被影响，也有可能会产生传导矛盾，使复杂矛盾问题的结构和和性质也随之发生变化.

定义1(矛盾问题集) 设有一复杂矛盾问题P_s，若其中包含有若干个子矛盾问题P₁, P₂, …, P_m，则这些子矛盾问题形成一个特殊的矛盾问题集合，称其为矛盾问题集，表示

$ \mathit{P} = \{ {\mathit{P}_{\rm{1}}}, {\mathit{P}_2}\mathit{, } \cdots, {\mathit{P}_\mathit{m}}\} . $

(2)

在一个复杂的工程矛盾问题P_s中，既存在着大量的矛盾问题(不相容问题)，也存在着一定数量和矛盾问题相关的非矛盾问题(即相容问题).所以P_s实际上是一个问题集合，如果用P表示其中的矛盾问题集合，用Q表示相容问题集合，显然有

$ {{P}_{\rm{s}}}=P\cup Q. $

(3)

定义2(独立矛盾) 设矛盾问题集P中有n(n≥2) 个矛盾，若P_i∈P(1≤i≤n)，且不存在P_j∈P(1≤j≤n且j≠i)和其相关，则称P_i为独立矛盾.

由独立矛盾组成的集合，称为独立矛盾集，用集合I表示.

定义3(相关矛盾) 设矛盾问题集P中有n(n≥2) 个矛盾，若P_i∈P(1≤i≤n)，至少存在一个P_j∈P(1≤j≤n且j≠i)或P_j∈Q和其相关，则称P_i为相关矛盾.

由相关矛盾组成的集合，称为相关矛盾集，用集合A表示.

显然有P=A∪I，复杂矛盾问题P_s的构成如图 1所示.

图 1 P_s的构成 Figure 1 Composition of P_s

2 矛盾信息元和矛盾信息元集

定义4(正向消除矛盾) 设有一矛盾问题，若条件特征量值(V_c)往增大的方向变化时有利于消除矛盾，则称这种方式为正向消除矛盾^[13].

定义5(负向消除矛盾) 设有一矛盾问题，若条件特征量值V_c往减少的方向变化时有利于消除矛盾，则称这种方式为负向消除矛盾^[13].

定义6(矛盾符号函数) 若用一个函数来表明矛盾消除时条件特征V_c变化的方向性，正向消除矛盾时，函数取值为正1；负向消除矛盾时，函数取值为负1，则称该函数为矛盾符号函数^[13]，表示为

$ \mathit{S}\left( {{\mathit{V}_\mathit{c}}, {\mathit{V}_d}} \right) = \left\{ {\begin{array}{*{20}{c}} { + 1} & {(正向消除矛盾时), }\\ { - 1} & {(负向消除矛盾时).} \end{array}} \right. $

(4)

定义7(矛盾度) 设在一个矛盾问题P₀中存在条件特征量值V_c(V_c > 0) 和目标特征量值V_d(V_d > 0)，若将差值(V_d-V_c)的归一化式子和矛盾符号函数S(V_c, V_d)结合，则可表征该矛盾体的矛盾程度，将其称为矛盾度^[13]，表示为

$ N = \mathit{S}\left( {{\mathit{V}_\mathit{c}}, {\mathit{V}_d}} \right)\frac{{{\mathit{V}_d} - {\mathit{V}_\mathit{c}}}}{{{\rm{max}}\left( {{\mathit{V}_\mathit{c}}, {\mathit{V}_d}} \right)}}. $

(5)

N的取值范围为：-1≤N≤1.

当N=1时，矛盾问题P₀处于绝对矛盾状态；

当N≤0时，矛盾问题P₀处于相容状态，即非矛盾状态；

当0 < N < 1时，矛盾问题P₀处于矛盾状态，即不相容状态(或对立状态).此时，N越大，表明矛盾问题的矛盾程度越大.

定义8(矛盾体) 在矛盾问题中，条件C和目标D这两个元素就构成了矛盾体，表示

$ \mathit{E} = \left( {C, D} \right). $

(6)

在E中，实现目标的条件C是用于破解矛盾的一方，称为矛方；目标D是矛盾中被破解的一方，称为盾方^[12].若E中只有一对矛盾特征，则称其为单特征矛盾体；若E中包含多对矛盾特征，则称其为多特征矛盾体.

定义9(矛盾信息元) 设有一单特征矛盾体E，矛盾符号函数为S(V_c, V_d)，矛盾度为N，若将三者组合形成一个基元，则该基元是矛盾体状态的信息描述，称其为矛盾信息基元模型，简称为矛盾信息元，表示为

(7)

其中，V_N表示矛盾度N的取值.矛方特征M_fc、盾方特征M_fd是描述矛盾体的主体特征，它们说明矛盾体对应双方的特征；矛盾度N用于说明矛盾双方的矛盾程度.

定义10(矛盾信息元向量) 设有一多特征矛盾体E，若将其中的每个矛盾特征对(M_{fc_i}, M_{fd_i})(i=1, 2, …, n)的矛盾状态都用一个矛盾信息元I_{M_i}来描述，则所有的I_{M_i}组成一个向量，称其为矛盾信息元向量，表示为

$ {\mathit{\boldsymbol{I}}_\mathit{v}} = \left( {{\mathit{I}_{{\mathit{M}_{\rm{1}}}}}, {\mathit{I}_{{\mathit{M}_2}}}{\rm{, }} \cdots {\rm{, }}{\mathit{I}_{{\mathit{M}_\mathit{n}}}}} \right), $

(8)

其中，

$ {\mathit{I}_{{\mathit{M}_\mathit{i}}}} = \left[{\begin{array}{*{20}{c}} E & {{M_{f{c_i}}}} & {{V_{{c_i}}}}\\ {} & {{M_{f{d_i}}}} & {{V_{{d_i}}}}\\ {} & {\mathit{S}\left( {{\mathit{V}_{{\mathit{c}_\mathit{i}}}}, {\mathit{V}_{{d_i}}}} \right)} & { \pm 1}\\ {} & {{N_i}} & {{V_{{N_i}}}} \end{array}} \right], \left( {i = 1, \cdots, n} \right). $

(9)

矛盾信息元和矛盾信息元向量是矛盾问题的抽象表达，它反映了矛盾问题的状态、特征和内涵.

由矛盾信息元或矛盾信息元向量组成的集合称为矛盾信息元集，可用B_I来表示,

$ {{B}_{I}}=\left\{ \left. {{I}_{{{M}_{\rm{1}}}}},{{I}_{{{M}_{2}}}},\cdots {{I}_{{{M}_{n}}}}\rm{,}{{\mathit{\boldsymbol{I}}}_{{{\mathit{v}}_{\rm{1}}}}},{{\mathit{\boldsymbol{I}}}_{{{\mathit{v}}_{\rm{2}}}}},\cdots ,{{\mathit{\boldsymbol{I}}}_{{{\mathit{v}}_{\mathit{m}}}}} \right\} \right.. $

(10)

3 矛盾状态图

定义11(均角平面坐标) 设在一个矛盾问题集合P中有n个矛盾，则这n个矛盾产生n个矛盾度.从平面的一个原点出发，用n个坐标轴均分整个平面，坐标轴之间的夹角为360°/n.n个坐标轴分别用来标示n个矛盾度，这样的坐标称为均角平面坐标^[12].

定义12(矛盾状态图) 把矛盾问题集合P中的每一个矛盾问题的矛盾度，标示在均角平面坐标对应的坐标轴上，然后用直线连接起来，形成一张矛盾度在均角平面的静态分布图.这是一张反映矛盾问题集合中矛盾问题的矛盾度态势的多向量图，把它称为矛盾状态图.

矛盾状态图是一种标示矛盾问题矛盾度的坐标图形方法.它既可以显示矛盾问题集合P中矛盾问题的分散性，也可以反映矛盾问题集合P中矛盾问题对应的矛盾度的分布状态.矛盾状态图可以作为一种有效工具来对矛盾问题集合P中的主次矛盾进行划分，而且还可以增加这一过程的可视性.另外，矛盾状态图也可作为分析矛盾问题矛盾度全程变化的形象化描述工具.

4 复杂矛盾问题的信息元表示

矛盾信息元(或矛盾信息元向量)是矛盾问题的信息表示，它反映了矛盾问题的本质和特征.只有掌握了矛盾信息元(或矛盾信息元向量)，才能了解矛盾问题的确切状态，为矛盾问题的分析和处理奠定基础.

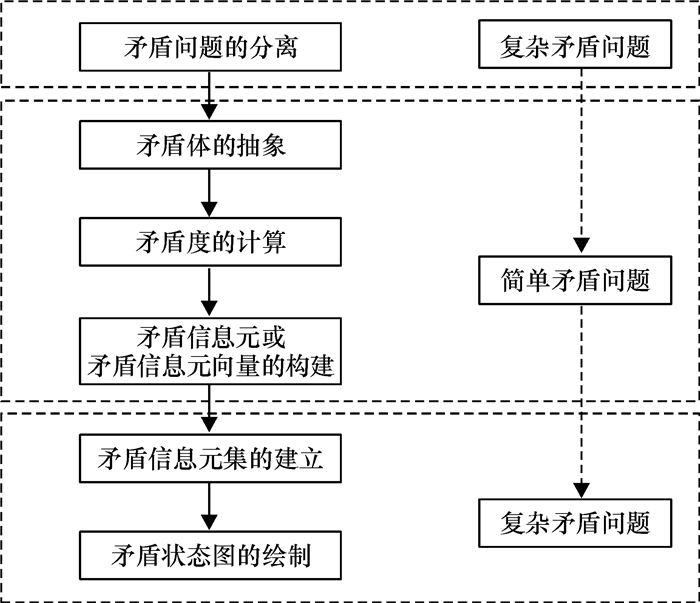
复杂矛盾问题的信息元表示要按照一定的方法和步骤进行，如图 2所示.

图 2 复杂矛盾问题的信息元表示步骤 Figure 2 Steps indicated by information unit of complex contradiction

1) 矛盾问题的分离

一般，工程活动的目标是既定和明确的，并且会规定评价标准及相应的参数指标, 假设用d_i(i=1, 2, …, n)表示.在工程活动中发现问题，关键是要寻找工程系统现行状态S₀所对应参数指标d_0i(i=1, 2, …n)与期望状态(即目标状态)S_e所对应参数指标d_ei(i=1, 2, …n)取值的差异.这种差异可用向量r_d来表示.

$ {\mathit{\boldsymbol{r}}_\mathit{d}} = \left( {{\mathit{r}_{\mathit{d}{\rm{1}}}}, {\mathit{r}_{\mathit{d}{\rm{2}}}}, \cdots {\rm{, }}{\mathit{r}_{\mathit{dn}}}} \right). $

(11)

若d_0i≠d_ei，令r_di=1；若d_0i=d_ei，令r_di=0.显然r_d=1是0，1向量，若r_di=1，则该参数指标d_i对应的问题记为S_i.若S_i在现有的条件下是没办法解决的，就确定为矛盾问题，将其归入矛盾问题集P，最后对P中的矛盾问题重新编号

$ P = \left\{ {\left. {{P_1}, {P_2}, \cdots {\rm{, }}{P_m}} \right\}} \right., \left( {n \ge m \ge 1} \right). $

(12)

矛盾问题集P之外的其他问题则写入相容问题集Q.

2) 矛盾体的抽象

对于P中包含的每个矛盾问题(即简单矛盾问题)，要进行矛盾体的抽象.矛盾体的抽象不仅是确定矛盾问题的矛方物元和盾方物元，还要对矛方物元和盾方物元所对应的矛盾特征进行性质上的明晰，并对其对应的特征量值进行客观的认定.

例1 2011年出台的广州城市交通状况整治工程方案的目标是“到2015年力争中心城区干道车速保持不低于25 km/h”，而目前晚高峰中心城区主干道平均车速约为21 km/h.

很明显这是一个矛盾问题，因为在现有的条件下根本无法达到目标车速.在这个矛盾问题中，目标车速(用D表示)是盾方；而现有的交通条件(用C表示)是矛方，所以此问题中的矛盾体：E=(C, D).

下面再来确定矛盾特征.

C对应的特征是当前车速(用M_fc表示)，其量值是21 km/h(用V_c表示)；D对应的特征是目标车速(用M_fd表示)，其量值是25 km/h(用V_d表示).

3) 矛盾度的计算

对于每个矛盾体，在明确了矛方、盾方及其矛盾特征和特征量值之后，还要对其产生的矛盾程度做计算和评估，也就是要计算出矛盾度N.

就例1的矛盾问题，显然条件特征量值V_c往增大的方向变化时有利于消除矛盾，所以S(V_c, V_d)取值为正1，矛方物元和盾方物元所对应矛盾特征的矛盾度为

$ N = \mathit{S}\left( {{\mathit{V}_\mathit{c}}, {\mathit{V}_d}} \right)\frac{{{\mathit{V}_d} - {\mathit{V}_\mathit{c}}}}{{{\rm{max}}\left( {{\mathit{V}_\mathit{c}}, {\mathit{V}_d}} \right)}} = \frac{{25 - 21}}{{25}} = 0.16. $

(13)

4) 矛盾信息元(或矛盾信息元向量)的构建

针对每个具体的矛盾问题，构建矛盾信息元(或矛盾信息元向量).

例1的矛盾信息元模型如下：

$ {\mathit{I}_\mathit{M}} = \left[{\begin{array}{*{20}{c}} E & {{M_{fc}}} & {{V_c}}\\ {} & {{M_{fd}}} & {{V_d}}\\ {} & {\mathit{S}\left( {{\mathit{V}_\mathit{c}}, {\mathit{V}_d}} \right)} & 1\\ {} & N & {{V_N}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} E & {{M_{fc}}} & {21}\\ {} & {{M_{fd}}} & {25}\\ {} & {\mathit{S}\left( {{\mathit{V}_\mathit{c}}, {\mathit{V}_d}} \right)} & 1\\ {} & N & {0.16} \end{array}} \right]. $

(14)

5) 复杂矛盾问题的信息元表示

复杂矛盾问题P_s中包含有多个矛盾问题，每个矛盾问题都可以用I_M(或I_v)来表示，因此可用类似的方法确定出各个矛盾信息元(或矛盾信息元向量)，最后将它们组合形成一个矛盾信息元集B_I.

矛盾信息元集B_I就是复杂矛盾问题P_s的信息元表示.

6) 矛盾状态图的绘制

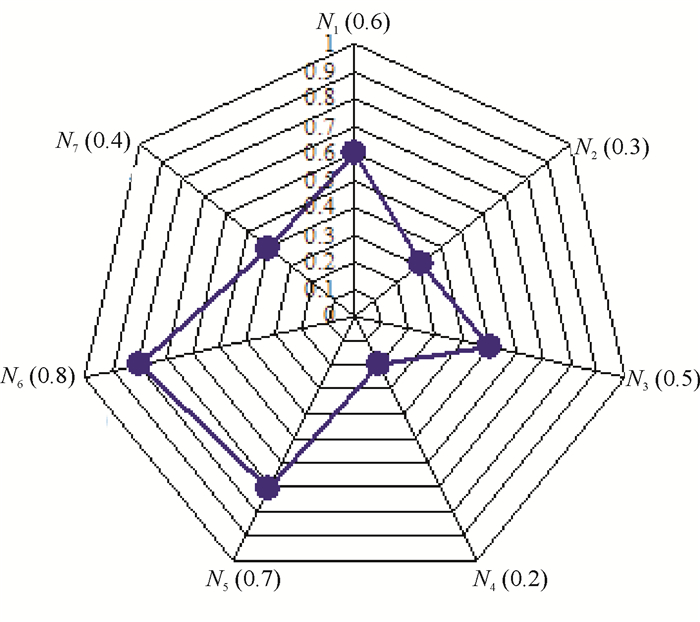
例2 设复杂矛盾问题P_s中包含有7个矛盾问题，且根据矛盾信息元集B_I获知它们的矛盾度分别为：

$ \begin{array}{l} \;\;\;\;{\mathit{N}_1} = 0.6, {\mathit{N}_2} = 0.3, {\mathit{N}_3} = 0.5, {\mathit{N}_4} = 0.2, {\mathit{N}_5} = \\ 0.7, {\mathit{N}_6} = 0.8, {\mathit{N}_7} = 0.4. \end{array} $

则该复杂矛盾问题P_s的矛盾状态图如图 3所示.

图 3 矛盾状态图 Figure 3 Contradiction state

从图 3可以清楚的看到复杂矛盾问题P_s当前的矛盾状态(以矛盾度表示).

5 结束语

本文针对工程活动中的复杂矛盾问题，首先给出了复杂矛盾的定义以及矛盾信息元和矛盾信息元集等反映其本质和内涵的一些重要概念，然后说明了复杂矛盾的信息元表示过程，为工程复杂矛盾的智能化处理奠定了基础.在接下来的工作中将对工程复杂矛盾问题分析和处理进行研究.

参考文献

[1]	DAVID K W N, CAI W. Treating Non-compatible Problem from Matter element Analysis to Extenics[J]. ACM SIGICE Bulletin, 1997, 22(3): 1-9.
[2]	CAI W. Extension theory and its application[J]. Chinese Science Bulletin, 1999, 44(17): 1538-1548. DOI: 10.1007/BF02886090.
[3]	杨春燕, 李卫华, 李小妹. 矛盾问题智能化处理的理论与方法研究进展[J]. 广东工业大学学报, 2011, 28(1): 86-92. YANG C Y, LI W H, Li X M. Recent research progress in theories and methods for the intelligent disposal of contradictory problems[J]. Journal of Guangdong University of Technology, 2011, 28(1): 86-92.
[4]	YANG C Y, CAI W. Extenics: Theory, Method and Application[M]. Beijing: Science Press, 2013: 1-5.
[5]	ALTSHULLER G S. 40 Principes: TRIZ Keys to Technical Innovation[M]. Worcester: Technial Innovation Center, 1999: 10-25.
[6]	韩华亭, 范海雄, 王葳, 等. 基于TRIZ理论的一种可调整支架的改进设计[J]. 机械设计与制造, 2010(2): 31-33. HAN H T, FAN H X, WANG W, et al. Improvement design of a kind of adjustable bracket based on the theory of TRIZ[J]. Machinery Design & Manufacture, 2010(2): 31-33.
[7]	韩彦良. TRIZ理论在螺旋输送机磨损问题中的应用研究[J]. 机械设计与制造, 2012(3): 201-203. HAN Y L. Application and research of TRIZ theory in wear of screw conveyor[J]. Machinery Design & Manufacture, 2012(3): 201-203.
[8]	POULIN D I, st-VINCENT P, BRATLEY P. Contradiction and confirmation[J]. Proceeding of the International Database and Expert Systems Applicatioins, 1993: 502-513.
[9]	CARMONAA P I, CANTRO J L, ZURITA J M. Contradiction semitime fuzzy model-based adapting control[J]. International Journal of Aprroximate Reasoning, 2002(6): 108-129.
[10]	PERLIS D, ANDERSON M, JOSYULA D, et al. Detecting, classifying and handling contradiction in a large dynamic information environment[J]. NTIS, 2006(10): 12.
[11]	ZENG T, WANG C G, YU Y Q. Charactersistics of contradictory information and its presentation[C]//Proceedings of 2009 International Conference on Signal Processing Systems.[S.l.]:ICSPS, 2009: 394-398.
[12]	曾韬. 工程活动中矛盾问题的形式化研究[D]. 广州: 广东工业大学计算机学院, 2011.
[13]	曾韬, 余永权, 赵锐. 工程矛盾的可拓模型及主要矛盾识别方法[J]. 广东工业大学学报, 2013, 30(3): 14-17. ZENG T, YU Y Q, ZHAO R. Extension model for engineering contradictions and the way of identifying the main contradiction[J]. Journal of Guangdong University of Technology, 2013, 30(3): 14-17.