说话人识别(Speaker Recognition)是一种利用说话人的语音特征与预先提取的说话人的语音特征相比较,进而确认和鉴别说话人身份的技术[1],被广泛应用于需要身份安全认证的领域.
在目前的说话人识别研究中,常用模型有高斯混合模型(GMM),隐马尔可夫模型(HMM),支持向量机模型(SVM)以及矢量量化模型(VQ).基于高斯混合模型(Gaussian Mixture Model, GMM) [2-3]的说话人识别利用多个高斯分布来拟合特征矢量的空间分布,可以达到较高的精度,是目前非常成功的与文本无关的说话人识别模型[4-5].
经典的GMM在对每个说话人建立模型时,其混合阶数K与具体应用有关,一般由实验来确定[6].但是,由实验获得一个固定值的GMM阶数K,具有很大的随意性.在建立模型过程中,固定的GMM阶数的建模方法并不符合说话人语音特征分布的多样性,会导致在每个说话人语音特征参数分布的聚类特性不同时出现模型过拟合或者欠拟合的现象[7].
为此,本文提出通过引进吸引子传播方法(Affinity Propagation, AP)[8]的思想,来自动获取说话人语音特征参数分布的聚类数目(也就是GMM的阶数K),并研究该聚类算法结合GMM的说话人识别效果.首先,在提取语音MFCC特征的基础上,采用AP聚类算法获取说话人语音MFCC特征参数的合理聚类数目;然后,将该聚类数目作为GMM的阶数作说话人识别实验.由AP聚类算法获得GMM的阶数,可针对不同说话人的所具有的不同语音特征分布,建立混合阶数不固定的模型结构,该模型能更好地拟合每一个说话人的具体特征分布,更符合因每个说话人发音特点的不同而造成声学特征参数聚类特性不同的实际场合.
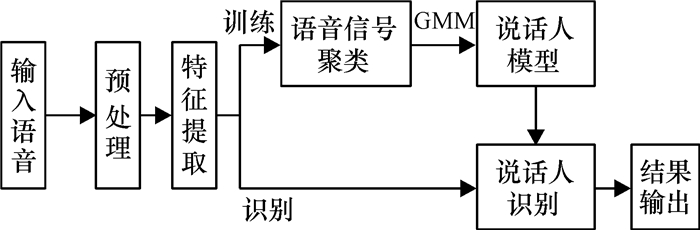
1 说话人识别算法经典的说话人识别算法一般包括4个部分[9-10]:预处理阶段,特征提取,参数训练,说话人识别.其设计流程如图 1所示.
|
图 1 设计流程图 Figure 1 Design flow chart |
Mel频率倒谱系数(MFCC)[11]是一种基于梅尔尺度的频域倒普参数,其充分利用了人耳的听觉特性,是目前声纹特征中识别率最高的一种[12-13].
在实频域范围内,当f<1 000Hz时,人的听觉系统的感知能力与f成线性关系,而当f>1 000Hz时却成对数关系.在整个Mel域,人耳的感知能力与Mel频率是成线性关系的.图 2所示为MFCC的提取过程.

|
图 2 MFCC特征提取流程图 Figure 2 The flow chart of MFCC feature extraction |
AP聚类算法是一种新的无监督聚类算法[14],在数据点的相似度矩阵上进行聚类.该算法在初始时将所有数据点看作潜在聚类中心,通过数据点间的消息传递逐步确定高质量聚类中心.算法的关键步骤是吸引度R=[r(i, k)](Responsibility)和归属度A=[a(i, k)](Availability)的迭代更新.r(i, k)和a(i, k),可由迭代公式(2)和(3)表示:
| $ s\left( {i,k} \right) = - {d^2}\left( {{x_i},{x_k}} \right) = - {\left\| {{x_i} - {x_k}} \right\|^2}, $ | (1) |
| $ r\left( {i,k} \right) = s\left( {i,k} \right) - \mathop {\max }\limits_{j \ne k} \left\{ {a\left( {i,j} \right) + s\left( {i,j} \right)} \right\}, $ | (2) |
| $ a\left( {i,k} \right) = \min \left\{ {0,r\left( {k,k} \right) + \sum\limits_{j \notin \left( {i,k} \right)} {\max \left\{ {0,r\left( {j,k} \right)} \right\}} } \right\}. $ | (3) |
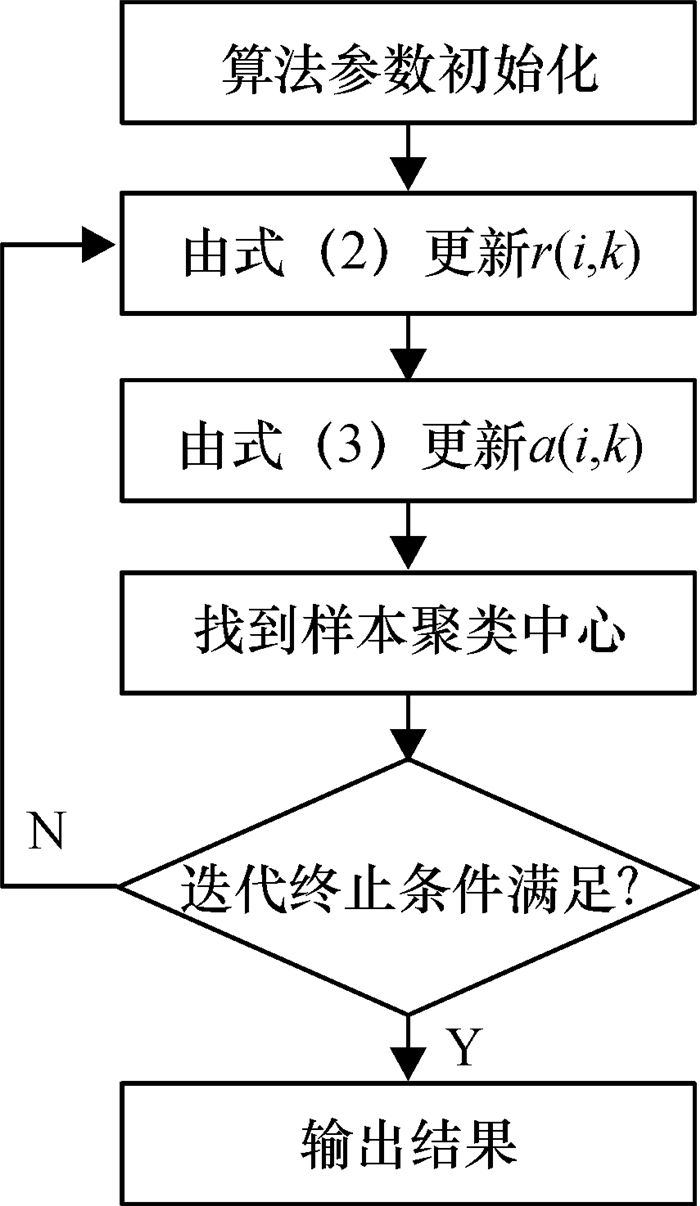
其中,s(i, k)为点i到点的相似度,用欧氏距离表示.吸引度R=[r(i, k)]表示从点i发送到候选中心点k的消息,反映k适合作为点i的聚类中心的程度;归属度A=[a(i, k)]表示从候选中心点k发送到点i的消息,反映点i选择点k作为其聚类中心的适合程度.在式(1)中,当i=k时,相似度矩阵S=[s(i, k)]对角线上的数值s(k, k)为偏向参数p(k),也称作参考度p(Preference).p(k)作为点k能否成为聚类中心的评判标准,一般地,p(k)值越大,这个点成为聚类中心的可能性也就越大.AP聚类算法流程如图 3所示.
|
图 3 AP聚类算法流程图 Figure 3 The flow chart of AP clustering algorithm |
高斯混合模型(GMM)建模基础是不同说话人语音特征矢量所具有的概率密度函数.首先,由AP聚类算法对语音特征矢量进行聚类;其次,分别求出每一类的均值、协方差矩阵和出现的概率,从而得到每个说话人的GMM模型;最后,将测试集代入得到的GMM模型进行模式匹配,找出最大后验概率.
一个K阶的GMM概率密度函数表示为
| $ P\left( {o\left| \lambda \right.} \right) = \sum\limits_{j = 1}^K {{\omega _j}{p_j}} ,\left( o \right),\left( {j = 1,2, \cdots ,K} \right). $ | (4) |
其中o为语音特征矢量,K为GMM混合阶数,ωj为混合权值.λ表示GMM模型,P(o|λ)表示o属于λ模型的概率.
一个K阶的GMM表示为
| $ \begin{array}{l} {\rm{GMM}} = \sum\limits_{j = 1}^K {{\omega _j}\frac{1}{{{{\left( {2{\rm{ \mathsf{ π} }}} \right)}^{K/2}}{{\left| {{\mathit{\Sigma }_j}} \right|}^{1/2}}}}} \times \\ \exp \left\{ { - \frac{1}{2}\left( {X - {\mu _j}} \right)\mathit{\Sigma }_j^{ - 1}\left( {X - {\mu _j}} \right)} \right\}. \end{array} $ | (5) |
其中μj为均值向量,Σj为协方差矩阵.故一个K阶GMM可由混合权值、均值向量和协方差矩阵表示
| $ {\lambda _j} = \left\{ {K,{\omega _j},{\mu _j},{\mathit{\Sigma }_j}} \right\}. $ | (6) |
GMM模型参数K已经由AP聚类算法从训练样本中获得,其余参数估计采用最大似然估计,即EM算法.在EM算法每次迭代时,有P(o|λ)≥P(o|λ),而迭代后得到的混合权值、均值向量和协方差矩阵表示为
| $ {\omega _k} = \frac{{\sum\limits_{i = 1}^N {\frac{{{\omega _k}{P_k}\left( {{X_i}} \right)}}{{\sum\limits_{k = 1}^K {{\omega _k}{P_k}\left( {{X_i}} \right)} }}} }}{N}. $ | (7) |
| $ {\mu _k} = \frac{{\sum\limits_{i = 1}^N {\frac{{{\omega _k}{P_k}\left( {{X_i}} \right)}}{{\sum\limits_{k = 1}^K {{\omega _k}{P_k}\left( {{X_i}} \right)} }}{X_i}} }}{{\sum\limits_{i = 1}^N {\frac{{{\omega _k}{P_k}\left( {{X_i}} \right)}}{{\sum\limits_{k = 1}^K {{\omega _k}{P_k}\left( {{X_i}} \right)} }}} }}. $ | (8) |
| $ {\mathit{\Sigma }_k} = \frac{{\sum\limits_{i = 1}^N {\frac{{{\omega _k}{P_k}\left( {{X_i}} \right)}}{{\sum\limits_{k = 1}^K {{\omega _k}{P_k}\left( {{X_i}} \right)} }}{{\left( {{X_i} - {\mu _i}} \right)}^2}} }}{{\sum\limits_{i = 1}^N {\frac{{{\omega _k}{P_k}\left( {{X_i}} \right)}}{{\sum\limits_{k = 1}^K {{\omega _k}{P_k}\left( {{X_i}} \right)} }}} }}. $ | (9) |
实验选用了两种不同的语音库:Timit标准语音库以及自制网络志愿者语音库.在以往实验中,一般认为K=32时,识别效果比较好[15].在此,对两种语音库分别都做了GMM模型阶数K=32以及K由AP聚类获得的识别实验.
实验测试的硬件环境:CPU为Intel(R) Core(TM) i7-3.4GHz,内存为32G,操作系统为Windows7旗舰版64位系统,编程软件为MATLAB R2013a.
2.1 采用Timit标准语音库的实验本次实验选取了Timit语音库中的80个说话人,每个说话人有10句语音,并抽取前8句作为训练样本,后2句作为测试样本.测试实验中,MFCC采样频率为8 kHz,帧长为240点(30 ms),帧移为80点(10 ms),每帧取24维的特征参数.
训练过程步骤如下:
Step1 得到训练样本.
Step2 AP聚类得到训练样本的类别数K.
Step3 将Ki作为第i个说话人GMMi的阶数,训练得到模型参数ωi、μi、Σi,i=1, 2, …, 80.
识别过程步骤如下:
Step1 得到测试样本.
Step2 获取第j个测试样本的GMMi值.把第j个测试样本代入阶数为Ki的的GMMi模型中,i, j=1, 2, …, 80.
Step3 输出当前测试样本代入GMMi后得到最大值所对应的i值.
Step4 判断i=j是否成立.是,则a=a+1,进入下一步;否,进入下一步.
Step5 判断j是否小于语音库里的人数80.是,则令j=j+1,并返回Step1;否,则进行下一步.
Step6 输出识别准确率
| $ R = \frac{a}{{80}} \times 100\% . $ | (10) |
| 表 1 Timit语音库实验结果对比 Table 1 The experimental results comparison of Timit standard speech library |
|
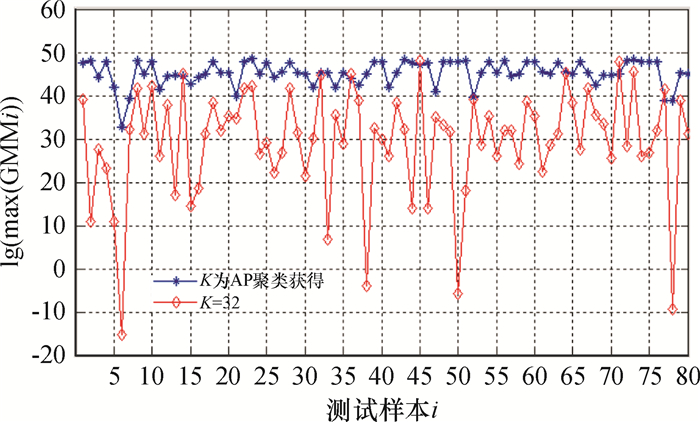
图 4 GMM阶数K对测试结果的影响 Figure 4 Influence of GMM order K on test results |
从表 1中可以看出,K=32时识别时间是要比K由AP聚类算法获得时快,但两种方法的的识别准确率均是100%.从图 4中比较两种GMM的阶数K对测试结果的影响,可知,使用AP聚类获得K值时的lg(max{GMMi})折线图基本位于K=32时的上方.这里的max{GMMi}可以理解为“区分度”,即max{GMMi}越大,则识别时出现误判的可能性越小.
由此可见,在使用AP聚类情况下,从总体效果来看,识别精度优于经验值K=32时的效果.
2.2 网络志愿者多方言语音库的实验本实验语音库构建是在百度贴吧上召集21名网络志愿者,21名志愿者均念了10句相同的古诗,并各自用其手机录音,其中18位用的是带不同口音的普通话念,另外3位则是用地方方言念.
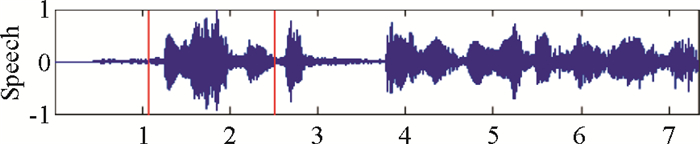
实验以MP3格式下载,通过试听可以发现,21名网络志愿者说话的口音较杂,说话环境喧杂,其中可明显听到走楼梯声、车声、电视机声、志愿者爆破音的喷麦声等杂音.另外,还发现有语音失真现象.选取一句原始样本的语音,为某网友所念的“弃我去者,昨日之日不可留”,在念此诗句时夹杂有走楼梯声以及喘息声.该句原始样本语音的波形如图 5所示.
|
图 5 某位志愿者一句原始语音波形 Figure 5 The original speech waveform of one volunteer |
21位网络志愿者同一句话语音因素在经过AP聚类算法聚类后得到的的类数各不相同,且有些显然不在K=32附近.AP聚类结果如表 2所示,其中第6位和第9位志愿者的语音是地方方言.
| 表 2 21位网络志愿者同一句话语音因素AP聚类后类别数表 Table 2 AP clustering category table of the same phonetic factors by 21 volunteers from network |
根据表 2的聚类结果,对21位志愿者的语音进行训练建模,得到{GMM1, GMM2, …, GMM21},进而作匹配识别实验.K=32和AP聚类获取K值两种方法的比较实验,结果如表 3及图 6.
| 表 3 自制网络志愿者语音库实验结果对比 Table 3 The experimental results comparison of self-made network volunteers' speech library |
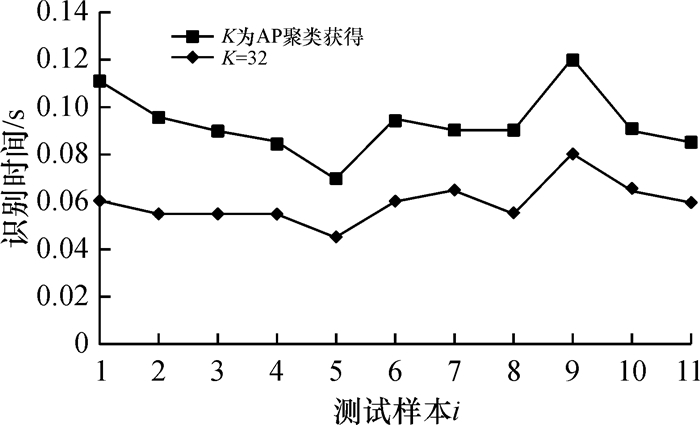
|
图 6 识别时间 Figure 6 The time of recognition |
实验结果显示,K=32时与K由AP聚类算法获得时的识别时间相差不大,但后者的识别准确率要显著优于前者.若是没有对每一个人的语音独立进行AP聚类获得类别数Ki,而是统一固定一个类别数K作为GMM的阶数,相对容易致使方言语音出现识别错误.当设置K=32时,第6和第9个用地方方言的语音在测试中容易出现误判,其音素分别为56和76.然而,在使用AP聚类算法时,由于每一个说话人模型拥有一个独立的类别数Ki,在纯净程度较差的现实语音中仍然能够较稳定得到较高的识别准确率.
图 7为GMM阶数K对测试结果的影响.
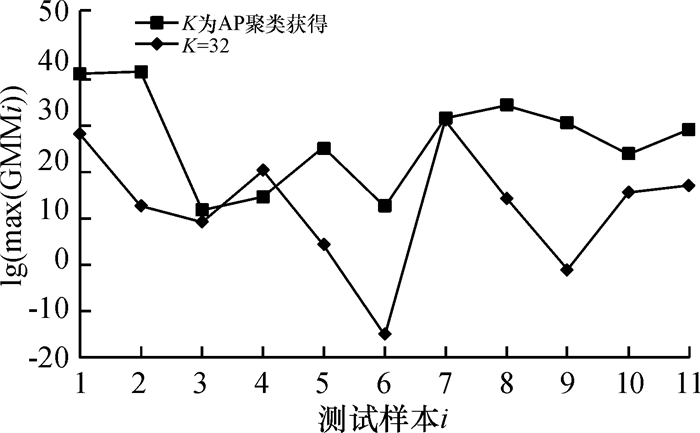
|
图 7 GMM阶数K对测试结果的影响 Figure 7 Influence of GMM order K on test results |
由图 7可知,21个测试样本中,有16个测试样本的max{GMMi}大于固定GMM阶数K=32的情况,有1个互相重叠,而另外4个也接近重叠.可见,比起固定阶数K=32,使用了AP聚类算法,得到的lg(max{GMMi})间的距离相对较大.
可见,AP聚类算法得到K值的方法显著优于固定值K=32的情况,特别是在多口音多语种的语音库中的识别效果远优于经验法得到阶数的识别效果.
3 结论针对经典的高斯混合模型(GMM)阶数确定的方法具有随意性的问题,引进吸引子传播聚类方法(AP聚类)来自动获取GMM的最佳阶数,提出一种融合AP和GMM的说话人识别的研究方法.本文的贡献在于:(1)采用AP聚类算法自动获取说话人的语音MFCC特征的类别数K,并将其作为GMM阶数,不必花费大量时间反复试验去获取一个合理的混合阶数;(2)比较了AP聚类算法获取阶数K与固定经验值K的说识别效果.实验表明,无论是标准的Timit语音库,还是自制网络志愿者语音库,AP聚类算法获取类别数K实际试验效果要优于固定经验值K,特别是在多口音多语种的现实语音中,AP聚类算法完全可自动获取一个理论上较优的类别数K.
实验结果证明了本文中选择AP聚类算法获取GMM阶数的合理性.论文的下一步工作在于自适应的多说话人识别的研究.
| [1] |
刘冰, 滕广超, 林嘉宇. 基于GMM的说话人识别系统设计与实现[J].
微处理机, 2014(3): 63-65.
Liu B, Teng G C, Lin J Y. Design and imple mentation of speaker identyfication system based on GMM[J]. Microprocessors, 2014(3): 63-65. |
| [2] | Reynolds D A, Quatier T F, Dram R B. Speaker verification using adapted Gaussian mixture models[J]. Digital Singal Processing, 2000, 10: 19-24. DOI: 10.1006/dspr.1999.0361. |
| [3] | Reynolds D A, Campbell W, Gleason T T. The 2004 MIT Lincoln laboratory speaker recognition system[A]. In Processdings of ICASSP. Philadel Phia. USA: [s. n. ], 2008. |
| [4] | Reynolds D A, Rose R. Robust text-independent speaker identification using Gaussian mixture speaker models[J]. IEEE Trans on Speech and Audio Processing, 1995, 3(1): 72-83. DOI: 10.1109/89.365379. |
| [5] |
吴慧玲, 杜成东, 毛鹤. 基于GMM的说话人识别算法的研究与应用[J].
现代计算机, 2014(5): 31-35.
Wu H L, Du C D, Mao H. Research and application of speaker recognition algorithm based on GMM[J]. Modern Computer, 2014(5): 31-35. |
| [6] |
曹洁, 潘鹏. 基于GMM的说话人识别技术研究[J].
计算机工程与应, 2011, 47(11): 114-117.
Cao J, Pan P. Research on GMM based speaker recognition technology[J]. Computer Engineering and Applications, 2011, 47(11): 114-117. DOI: 10.3778/j.issn.1002-8331.2011.11.033. |
| [7] |
王韵琪, 俞一彪. 自适应高斯混合模型及说话人识别应用[J].
通讯技术, 2014, 47(7): 738-743.
Wang Y Q, Yu Y B. Adaptive gaussian mixture model and its application in speaker recognition[J]. Communication Technology, 2014, 47(7): 738-743. |
| [8] | Frey B, Dueck D. Clustering by passing messages between data points[J]. Science, 2007, 315(5184): 972-976. |
| [9] |
刘荣辉, 彭世国, 刘国英. 基于智能家居控制的嵌入式语音识别系统[J].
广东工业大学学报, 2014, 31(2): 49-53.
Liu R H, Peng S G, Liu G Y. Embedded speech recognition system based on smart home control[J]. Journal of Guangdong University of Technology, 2014, 31(2): 49-53. |
| [10] | Zhong Y C, Hua X. Study on speech control of turning movements of the multifunctional nursing bed[J]. Advances in Intelligent and Soft Computing, 2012(1): 67-72. |
| [11] | Agrawal U K, Chandra M, Badgaiyan C. Fractional fourier transform combination with MFCC based speaker identification in clean environment[J]. International Journal of Advanced Science, Engineering and Technology, 2012, 1(1): 26-28. |
| [12] | Yuan Y J, Zhao P H, Zhou Q. Research of speaker recognition based on combination of LPCC and MFCC[C]//Proc of IEEE International Conference on Intelligent Computing and Intelligent Systems. [S. l. ]: IEEE Press, 2010: 765-767. |
| [13] |
李云, 鲍鸿. 语音分组识别技术的研究[J].
广东工业大学学报, 2014, 31(2): 54-57.
Li Y, Bao H. Research on speech recognition by group technology[J]. Journal of Guangdong University of Technology, 2014, 31(2): 54-57. |
| [14] |
郭秀娟, 陈莹. AP聚类算法的分析与应用[J].
吉林建筑大学学报, 2013, 30(4): 58-62.
Guo X J, Chen Y. Analysis and application on AP clustering algorithm[J]. Journal of Jilin Jianzhu University, 2013, 30(4): 58-62. |
| [15] |
陈觉之, 张贵荣, 周宇欢. 基于GMM模型的自适应说话人识别研究[J].
计算机与现代化, 2013(7): 91-93.
Chen J Z, Zhang G Y, Zhou Y H. Research on adaptive speaker recognition based on GMM[J]. Computer and Modernization, 2013(7): 91-93. |
 2015, Vol. 32
2015, Vol. 32