2. 广州船舶及海洋工程设计研究院,广东 广州 510250;
3. 华中科技大学 计算机科学与技术学院,湖北 武汉 430074
2. Guangzhou Marine Engineering Design & Research Institute, Guangzhou 510250, China;
3. School of Computer Science & Technology, Huazhong University of Science and Technology, Wuhan 430074, China
在船舶结构疲劳强度分析过程中,首先是前处理,对要进行疲劳分析的区域进行网格划分,进行数学建模;然后再对数学模型进行基于有限元求解的计算分析;最后是后处理,把所求的结果转化成图形网格,对其进行分析.
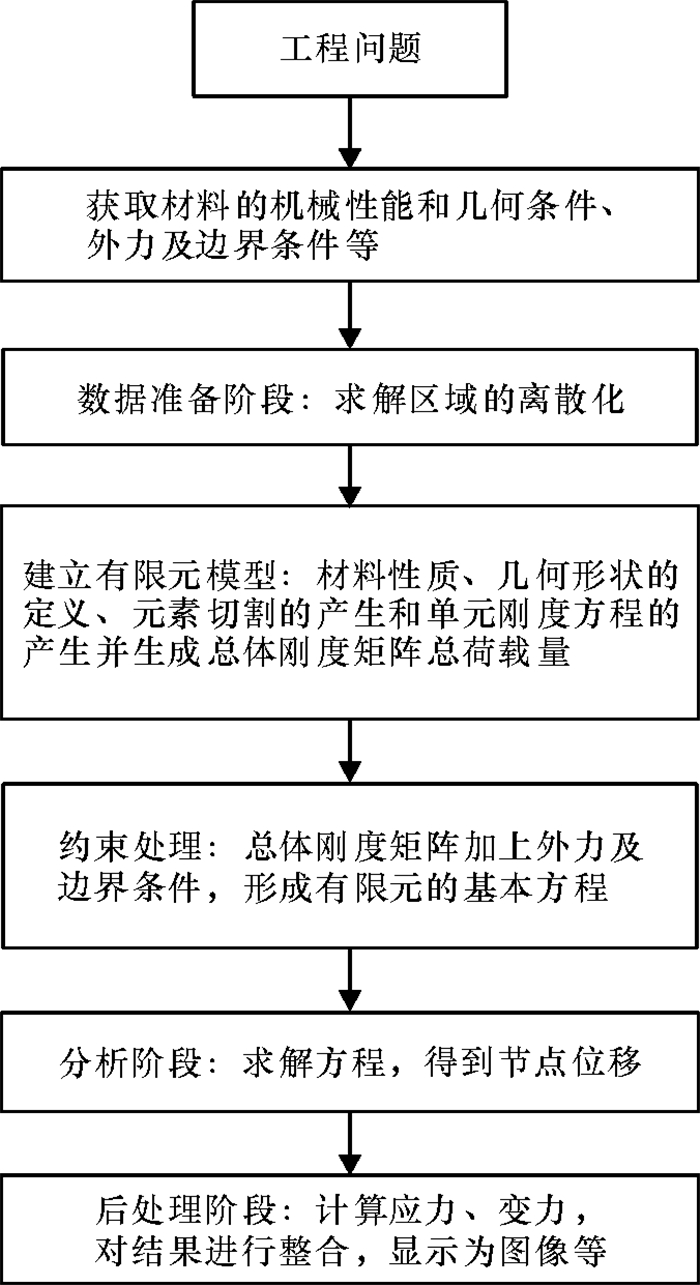
有限元法[1]是研究船舶疲劳分析的高效和快速方法之一.有限元法是R.Courant在1943年首先提出的,具体分析过程如图 1所示.其基本思想是:将连续体或结构划分为若干有限大小的元素,把连续待解区域离散化并且按照一定的方式结合在一起形成平衡方程,再加上边界条件进行求解[2-3].在船舶疲劳分析中,有限元的求解过程可以归结为求解线性方程组Ax=b的过程,此类线性方程组具有稀疏性并且计算规模非常庞大.
|
图 1 有限元分析流程图 Figure 1 Flow chart of finite element analysis |
从有限元法的理论和实践上分析可知,大部分时间耗费在数值计算上.对于船舶疲劳分析来说,大部分时间是花费在线性方程组的预处理以及迭代求解或直接求解上.船舶疲劳分析产生的线性方程组,往往是大规模的,并且是稀疏的.传统计算机由于受到CPU的计算速度和存储空间的限制,在使用有限元软件进行船舶疲劳分析时,常常因为问题规模的庞大、存储空间的不足导致计算时间过长,甚至无法计算分析[4].超级计算机的产生在一定程度上可以解决这个问题,但在科学计算过程中,产生的额外计算和附加存储空间,在一定程度上降低了计算效率.针对以上情况,本文研究在开源有限元软件Calculix[5]的基础上,对线性方程组迭代算法的预处理技术进行并行化改进,提出基于列主元的多行双门槛不完全LU分解预处理技术,对其参数进行优化,并且基于广州超级计算先导系统搭建有限元分析平台进行实际算例的实验测试,验证其可以有效提高求解线性方程组的速度.
1 相关工作国内外有不少关于有限元求解器移植到超级计算机的尝试.文献[6]提出了在Linux集群技术构建的高性能计算平台下,Ansys[7]分布式计算的关键配置和应用,并对如何发挥其并行优势提出了建议.在有限元软件并行化方面,上海超算中心联合上海交大进行的有限元并行应用改造试验[8-9].他们使用商业有限元软件Nastran在“神威Ⅰ”超级计算机系统进行了移植和并行计算功能的二次开发.
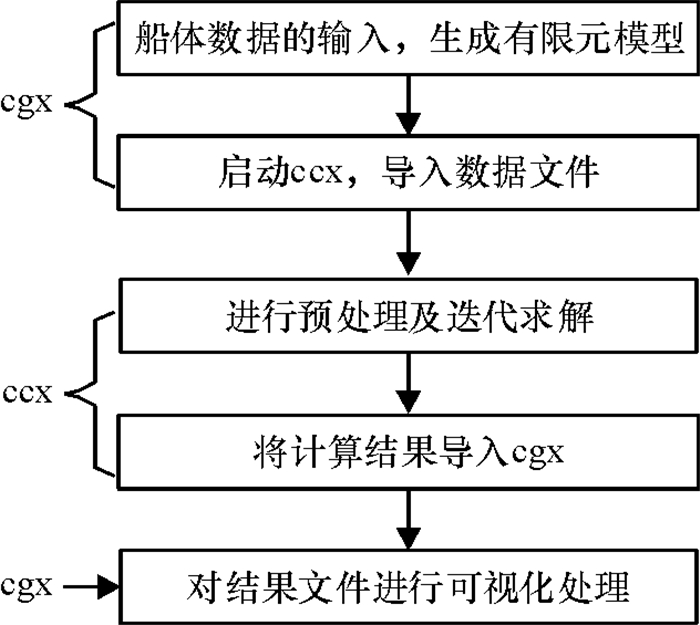
Calculix有限元求解器的工作流程如图 2所示.分前处理、数学模型求解和后处理3个阶段.前处理将产生一个有限元模型几何体的全过程,可以输入物理特性、描述边界条件和载荷来对模型进行修正,该部分可以使用Calculix的cgx模块完成,也可以二次开发,从其他有限元软件输入模型数据,比如Abaqus.Calculix的ccx模块接收前处理后的文件,生成数学模型,通过I/O读取矩阵文件,调用函数对矩阵进行预处理,预处理后再进行迭代求解.后处理模块可将计算结果以粒子流迹显示、梯度显示、彩色等值线显示、立体切片显示、矢量显示、透明及半透明显示等图形方式显示,也可将计算结果以图表、曲线形式显示或输出.
|
图 2 Calculix工作流程图 Figure 2 Calculix working flow chart |
Calculix有限元求解器的求解时间大部分花费在求解线性方程组上的.求解线性方程组的方法一般分为两类,一类是直接法[10],有LU分解、QR分解等.另外一类是迭代法[11],有Jacobi迭代、Gauss-Seidel迭代、SOR迭代和共轭梯度法等.直接法可以得到线性方程组的精确解,但是在问题规模非常庞大的情况下,直接法在分解过程中线性方程组很难保持其稀疏性,还会增加额外的存储空间和计算量.迭代法得到的解不如直接法精确,但是可以结合预处理技术, 在较少的步骤内达到收敛并且达到精度要求.在船舶疲劳强度分析中,线性方程组的阶基本都是非常大的,在时间上和空间上,选择迭代法可以取得最优.
预处理技术[12]是将线性方程组
| $ \mathit{\boldsymbol{Ax}} = \mathit{\boldsymbol{b}} $ | (1) |
进行转换,使其与某一线性方程组同解.但是,转换后的方程组必须更易于迭代求解,产生的这个转换矩阵就是预条件子.如果M为一个在某种程度上和A近似的非奇异矩阵,那么预处理后的线性方程组
| $ {\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{Ax}} = {\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{b}} $ | (2) |
的解与线性方程组(1)相同,就称M为预条件子.
线性方程组的预处理技术[13]主要有:填充元缩减策略、匹配技术、因子分解近似逆条件子构造等等.在预处理技术中,不完全LU分解是比较常用的.假设矩阵A的n-1个顺序主子式不为0,那么矩阵A可以唯一地分解为一个下三角矩阵L和下上三角矩阵U的乘积,即
| $ \mathit{\boldsymbol{A}} = \mathit{\boldsymbol{LU}}, $ | (3) |
其中,
| $ \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} 1&{}&{}&{}&{}\\ {{l_{21}}}&1&{}&{}&{}\\ {{l_{31}}}&{{l_{32}}}&1&{}&{}\\ \vdots&\vdots&\vdots&\ddots &{}\\ {{l_{n1}}}&{{l_{n2}}}&{{l_{n3}}}& \cdots &1 \end{array}} \right], $ |
| $ \mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} {{u_{11}}}&{{u_{12}}}&{{u_{13}}}& \cdots &{{u_{1n}}}\\ {}&{{u_{22}}}&{{u_{23}}}& \cdots &{{u_{2n}}}\\ {}&{}&{{u_{33}}}& \cdots &{{u_{3n}}}\\ {}&{}&{}& \ddots&\vdots \\ {}&{}&{}&{}&{{u_{nn}}} \end{array}} \right]. $ |
分解的一般形式为
| $ {l_{ij}} = {a_{ij}} - \sum\limits_{k = 1}^{j - 1} {{l_{ik}}{u_{kj}}\left( {i,j = 1,2,3, \cdots n;i \ge j} \right)} , $ | (4) |
| $ \begin{array}{l} \ \ \ \ \ \ \ {u_{ij}} = \left( {{a_{ij}} - \sum\limits_{k = 1}^{i - 1} {{l_{ik}}{u_{kj}}} } \right)/{l_{ii}}\left( {i = 1,2,3 \cdots n;j = 2,} \right.\\ \left. {3,4 \cdots n;i < j} \right). \end{array} $ | (5) |
令误差矩阵Q=L′U′-A满足一定的条件限制,例如某些特定位置的元素值为零,则称A=L′U′为不完全LU分解.
在不完全LU分解中,选择合适的填充元缩减策略十分重要.现有的填充元缩减策略[14]有:无填充的舍弃策略,它的收敛速度很慢,而且还可能不收敛;多层填充的舍弃策略,这种方法会遇到填充元的数量不可预计的问题;双门槛的舍弃策略[15],则很难找到最佳的参数值并且很难在每一行中保留同样的非零元个数.文献[16]Zha N和Yue TX使用不完全Cholesky分解进行矩阵预处理,但是只能适用于具有对称性的线性方程组.文献[17]实现的并行预处理,只适合在主对角占优矩阵进行.文献[18]使用SSOR预处理矩阵,但是仅适用于H-矩阵.文献[19]中,提出了基于GPU的稀疏线性系统求解预处理线性方程组的方法仅在单机上实现,加速效率有一定局限性.Ail[20]等实现了多GPU上的求解线性方程组,但是并未实现并行预处理技术,遇到病态线性方程组则很难实现求解.上述预处理方法中,很多都只适用于特定的线性方程组,而在船舶结构疲劳强度分析过程中的线性方程组是一般的方程组,很少具备对称性等.而不完全LU分解技术适合一般线性方程组的求解.在不完全分解预处理技术上,吴建平[21]提出了多行双门槛舍弃策略的MRILUT(b, p, τ),但是却无法保证线性方程组的主元相对于其他元素是比较大,甚至如果主元是零的话,分解就无法进行下去.并且随着矩阵分解的进行,分解后的矩阵稀疏性会有所变化,下三角矩阵元素会逐渐增加,上三角矩阵元素会越来越少,使用固定参数p无法保证公平的对矩阵元素进行舍弃.另外,针对单机上GPU加速效率的局限性,可以使用超级计算机先导系统平台来解决.
本研究提出了改进的预处理技术——基于列选主元的多行双门槛预处理技术,使用列选主元法和动态的舍弃策略进行不完全LU分解,给出其核心算法,并证明其有效性,最后通过在超级计算机先导系统平台上的实际算例验证其性能有效提升.
2 列选主元的多行双门槛舍弃策略 2.1 算法可行性在矩阵进行不完全分解时,依赖于对角元素的大小.具有对角优势的矩阵,分解后的元素比较精确,但是实际上在有限元法过程中的矩阵很难都满足对角元素占优,当对角优势变弱时,有效性大大降低甚至有时可能对角元素为零,导致矩阵分解中断.于是,引进列选主元的方法是解决此问题的有效途径.在说明算法可行性前,先介绍以下定理.
定理1 对矩阵A施行行(列)初等变换,相当于左(右)乘以一个相应的初等矩阵.
定理2 矩阵A∈Rn×n,存在n阶初等排列阵P,使得PA严格对角占优,则矩阵A拟严格对角占优.
定理3 矩阵A的所有顺序主子式不为0,那么矩阵A可以唯一地分解为一个下三角矩阵L和上三角矩阵U的乘积.
定理1、定理2和定理3的证明参阅文献[22].
矩阵A的列选主元过程,是在矩阵的某一列中选择元素最大的元素,然后进行行互换.那么由定理1可知,每一次进行选主元则可以看成一次矩阵的初等变换,那么就存在初等矩阵P1使得P1A为选主元后的结果.经过n次选主元后,矩阵A则排列成Pn… P1A.令P=Pn…P1,由定理2可知PA严格对角占优,那么矩阵A拟严格对角占优,则矩阵A的所有顺序主子式不为0.由定理3可知,矩阵A可唯一分解.这样,基于列选主元的多行双门槛预处理技术是可以进行下去的.
2.2 改进的MRILUT (b, p, τ) 2.2.1 改进方案在线性方程组进行迭代求解前,往往需要对其进行预处理.首先对矩阵进行划分,再对各个部分进行列选主元,然后对矩阵元素进行第一次舍弃策略,满足舍弃策略的矩阵元素留下来进行不完全LU分解,另一方面对已完成分解L和U中的某几行元素进行第二次舍弃策略.这里我们对两次舍弃策略进行优化,第一次舍弃策略采用τ与矩阵的谱范数的乘积作为界限,舍弃小于此界限的矩阵元素.第二次舍弃策略则使用动态的多行舍弃策略,根据矩阵某几行非零元素个数与参数q的乘积作为界限,超过此界限的矩阵元素则舍弃.经过两次舍弃策略后,把各个部分的计算结果进行归约,得到的矩阵为最终的预处理矩阵,供线性方程组进行迭代求解使用.
2.2.2 分解过程中的舍弃策略在矩阵分解时,对矩阵元素进行判断,通常舍去幅度较小的元素,但是这种做法开销特别大,并且当门槛越来越小的时候,趋近于直接法,无法达到控制存储和减少计算量的目的.针对这种情况,引入矩阵谱范数作为舍弃参数.矩阵范数的相关定义参考文献[22].
定义1 矩阵A∈Rn×n上的某个非负实值函数N(A)≡‖A‖, 任意的n阶矩阵A, B满足条件:
(1) 正定性:‖A‖≥0,当且仅当A =0时,‖A‖=0;
(2) 齐次性:‖cA‖=‖c‖×‖A‖,c为任意实数;
(3) 三角不等式:‖A+B‖≤‖A‖+‖B‖;
(4) 相容性:‖AB‖≤‖A‖×‖B‖;
则称N(A)≡‖A‖为Rn×n上的一个矩阵范数.
矩阵范数是描述矩阵扰动灵敏度的特征数,是解方程组和研究与探讨方程组本身性质的重要工具.虽然预处理的迭代法可以提高计算效率,但是相对也引入舍弃误差.除了通过列主元法来减少误差之外,还可以通过矩阵范数来控制预处理的舍入误差.由文献[22]可知谱范数满足定义1,因此它是一个矩阵范数.使用矩阵谱范数来作为参数,取τ(0<τ<1),当矩阵元素小于τ与矩阵的谱范数的乘积时,则舍弃;反之,则留下.这样就可以减少矩阵的条件数,并且改善一些病态方程,还可以控制不完全LU分解的误差.
2.2.3 分解后的动态舍弃策略对已分解完成的矩阵L和U分别保留p个绝对值较大的元素.在实际分解过程中,上三角矩阵的非零元素会随着分解的进行而减少,而下三角矩阵却相反.针对这种情况,应该对参数p进行实时的更新.对于分解因子L,
| $ p = q \times {\rm{rowl}}{\rm{.}} $ | (6) |
对于分解因子U,
| $ p = q \times {\rm{rowu}}{\rm{.}} $ | (7) |
其中,取p(0<p<1),而rowu为上三角矩阵中的某几行非零元素个数,rowl为下三角矩阵中的某几行非零元素个数,参数q预先设定.
当矩阵的某几行元素数已经完成不完全LU分解时,对rowu和rowl进行实时更新,再计算出p,把这几行的元素个数与p相比较.若超过p,则计算出差值,舍弃与差值相等的元素个数,其中舍弃的元素的值是原有元素中相对较小的.
2.3 算法收敛性在对线性方程组进行预处理时,必须保证线性方程组的迭代求解是收敛的,否则,该预处理是不可行的.在证明收敛性前,介绍如下定理:
定理4 矩阵A∈Rn×n是对角占优,那么分解过程中产生的矩阵A1, A2, …, An, 都是对角占优的.
定理4的证明易用数学归纳法得出.
定理5 如果矩阵A与分解后的矩阵M为对角占优,则ρ(B-1Q)≤ρ(B-1Q)<1.
证明:由于A =L∑U -Q=B -Q是正则分裂,所以ρ(B-1Q)<1.下证ρ(B-1Q)≤ρ(B-1Q):若要证ρ(B-1Q)≤ρ(B-1Q)只需证B-1Q≤B-1Q;若要证B-1Q≤B-1Q,只需证Q<Q,B-1≤B-1.
(1) 现证Q≤Q:
显然0≤Q, 0≤Q,所以只需证qijk≤qijk(k=2, …n+1).
令Z={(i, j)1≤i≠j≤n}.
① 对角元素,即i=j:
| $ q_{ii}^k = \sum\limits_{\begin{array}{*{20}{c}} {p \equiv k}\\ {\left( {i,p} \right) \notin J} \end{array}}^n {{l_{ik}}a_{kp}^{\left( {k - 1} \right)}} ,\bar q_{ij}^k = \sum\limits_{\begin{array}{*{20}{c}} {p \equiv k}\\ {\left( {i,p} \right) \notin J} \end{array}}^n {{{\bar l}_{ik}}\bar a_{kp}^{\left( {k - 1} \right)}} , $ | (8) |
由于
| $ q_{ii}^k \le \sum\limits_{\begin{array}{*{20}{c}} {p \equiv k}\\ {\left( {i,p} \right) \notin J} \end{array}}^n {{l_{ik}}a_{kp}^{\left( {k - 1} \right)}} \le \sum\limits_{\begin{array}{*{20}{c}} {p \equiv k}\\ {\left( {i,p} \right) \notin J} \end{array}}^n {{{\bar l}_{ik}}\bar a_{kp}^{\left( {k - 1} \right)}} , $ | (9) |
所以
| $ q_{ii}^k \le \bar q_{ii}^k. $ | (10) |
② 非对角元素,即i≠j:
当(i, j)∈Z∩(i≠j)时,
| $ q_{ij}^k = \bar q_{ij}^k = 0. $ | (11) |
当(i, j)∉ Z∩(i≠j), k≤i, j≤n时,
| $ q_{ij}^k = {l_{ik}}a_{kj}^{\left( {k - 1} \right)},\bar q_{ij}^k = {{\bar l}_{ik}}\bar a_{kj}^{\left( {k - 1} \right)}. $ | (12) |
由于
| $ q_{ij}^k \le {l_{il}}a_{kj}^{\left( {k - 1} \right)} \le {{\bar l}_{ik}}\bar a_{kj}^{\left( {k - 1} \right)}, $ | (13) |
所以
| $ q_{ij}^k \le q_{ij}^k. $ | (14) |
由式(10)、(11)、(14)可知Q≤Q.
(2) 再证B-1≤B-1:
| $ B = L\sum U ,\bar B = \bar L\sum {\bar U} . $ | (15) |
令
| $ U = U - {U_\alpha },L = I - {L_\alpha }, $ | (16) |
| $ \bar U = I - {{\bar U}_\beta },\bar L = I - {{\bar L}_\beta }. $ | (17) |
其中,Uα、Uβ是严格上三角矩阵,Lα、Lβ是严格下三角矩阵.
因为Uα≤Uβ, Lα≤Lβ, 由式(16)可得,
| $ \begin{array}{l} \ \ \ \ \ \ \ {U^{ - 1}} = {\left( {I - {U_\alpha }} \right)^{ - 1}} = I + {U_\alpha } + \cdots + {\left( {{U_\alpha }} \right)^{n - 1}} \le \\ I + {U_\beta } + \cdots + {\left( {{U_\beta }} \right)^{n - 1}} = {\left( {I - {U_\beta }} \right)^{ - 1}}, \end{array} $ | (18) |
所以
| $ {U^{ - 1}} \le {{\bar U}^{ - 1}}. $ | (19) |
由式(19)可知,U-1≤U-1.同理,可得L-1≤L-1.所以有B-1≤B-1.
综上所述,B-1Q≤B-1Q,于是ρ(B-1Q)≤ρ(B-1Q).
定理6 线性方程组Ax=b的基本迭代法方程xk=Bxk-1+f收敛的充要条件为ρ(B)<1.
定理6的证明参考文献[23].
基于列选主元的多行双门槛预处理技术中,使用列主元法保证矩阵是对角占优的,再由定理4、定理5和定理6可知基于列主元的多行双门槛预处理应用于迭代法最终可以达到收敛.
以上算法改进可以在Calculix中的模块ccx中实现.ccx通过调用Arpack接口来进行线性方程组的求解.由于ccx是开源软件,只需对Arpack中的preconditioning函数进行修改并且调用它,就可以完成矩阵的预处理,最后再调用并行程序进行迭代计算求解.
2.4 基于列主元的多行双门槛不完全LU分解算法由于Calculix有限元求解器开源,可以在其ccx模块对其代码进行并行化修改.在算法实现之前初始化MPI,使用FrontMtx_MPI_split函数对矩阵进行划分,分配到各节点上,然后各节点再进行preconditioning()进行矩阵的预处理,preconditioning()算法中一些函数的功能如下介介绍:column pivoting()对矩阵进行列选主元;abandon strategy()对多个行向量进行谱范数条件下的舍弃策略;dynamic abandon strategy()对上三角矩阵和下三角矩阵进行多行的动态舍弃策略.最后使用FrontMtx_MPI_Reduce函数对各节点的结果进行归约,得到最终结果,然后调用并行程序进行迭代求解.
ccx模块的预处理部分并行化修改的核心算法描述如下:
Function preconditioning(n,b,A)
for i=1:n
aii=column pivoting(A)
α=ai
For k=1:i-1 and when αk≠0
αk=αk /akk
abandon strategy(αk)
ifαk ≠0 thenα=α-αk*uk
end for k
abandon strategy(α)
if z==b then dynamic abandon strategy(α)
for j=1:i-1
lij=uij
for j=i:n
uij=α
end for i
3 实验分析 3.1 国家超级计算广州中心先导系统简介TH-1/GZ先导系统[24]由2个登录结点、512个计算结点和一些存储结点所组成.所有的计算结点和I/O服务结点通过天河高速互联网络互连这种高性能通信互联技术.
登录结点安装了RedHat Enterprise Linux 5.5 x86_64版本操作系统,定制了安全策略,遵循POSIX、LSB等标准,提供了64位程序开发与运行环境.计算结点为了保证计算效率,安装的是RedHat Enterprise Linux 5.5 x86_64版本精简操作系统.
2个登录结点为8路8核共计64核的SMP架构服务器.计算结点配置为两个6核Intel Xeon X5670处理器,运行频率2.93 GHz,共计12核,配备24 GB内存和Tesla M2050 GPU加速处理器一块,显存3 GB.全系统共计1 024个CPU和512个GPU,内存容量13.8 TB,其中CPU提供高性能的指令级并行计算能力,GPU主要提供高性能的数据级并行计算能力,支持异构融合计算,单结点综合计算能力655.6 GFlops,全系统浮点峰值性能335.7 TFlops.
先导系统的软件系统包括操作系统、编译系统、资源管理系统、程序开发环境、文件系统等,支持广泛的第三方软件,使开源有限元求解器Calculix在先导系统上的进行高性能计算是可行的.
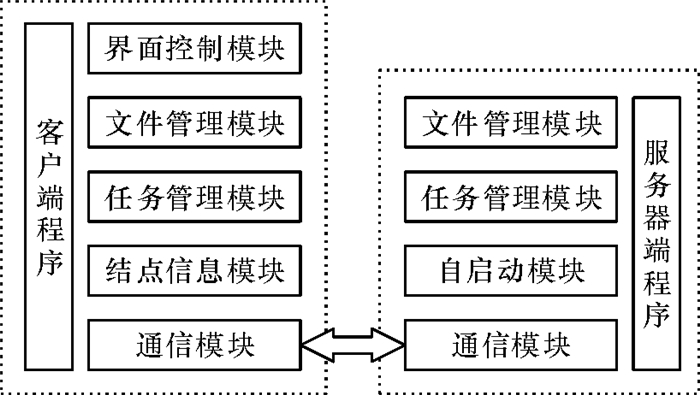
3.2 原型系统搭建基于C/S(Client/Server)模式的有限元分析平台,使用户能够更好地在PC上使用部署在超级计算机先导系统上的有限元分析系统,实现在本地机上实时地使用有限元分析系统,平台功能模块如图 3所示.
|
图 3 基于C/S模式的有限元平台功能模块 Figure 3 The finite element platform function module based on C/S model |
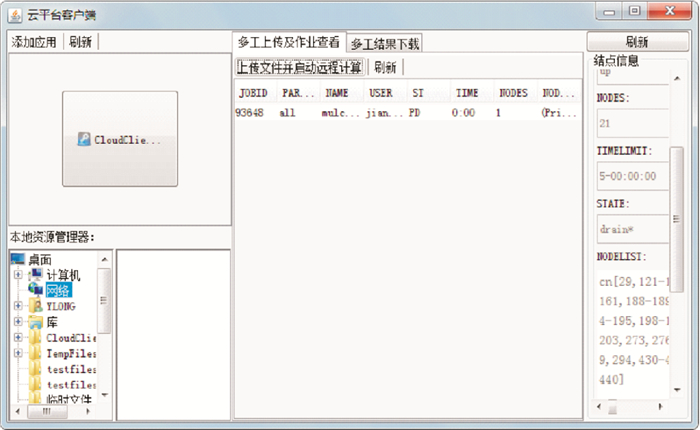
客户端可以让用户实时方便地上传提交任务,设置需要申请的计算节点数和核数.用户登陆VPN时,服务器端程序就会自动启动,实时检测用户需求,并且反馈结果给客户端.客户端友好界面如图 4所示.
|
图 4 客户端界面 Figure 4 The client interface |
本文的有限元实验分析基础资源环境为广州超算中心先导系统.本次实验100个大量的船体相关组件模型作为算例分别进行测试,测试中采用计算5次求平均值的方法,其中3个测试算例模型图如图 5~图 7所示.3个测试算例的详细分析如下:

|
图 5 算例A模型图 Figure 5 Model of Example A |
|
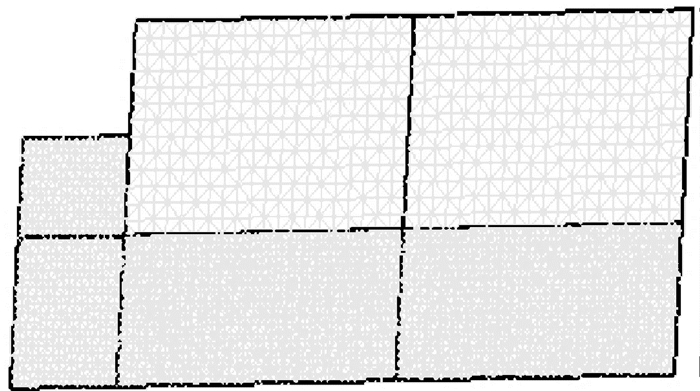
图 6 算例B模型图 Figure 6 Model of Example B |
|
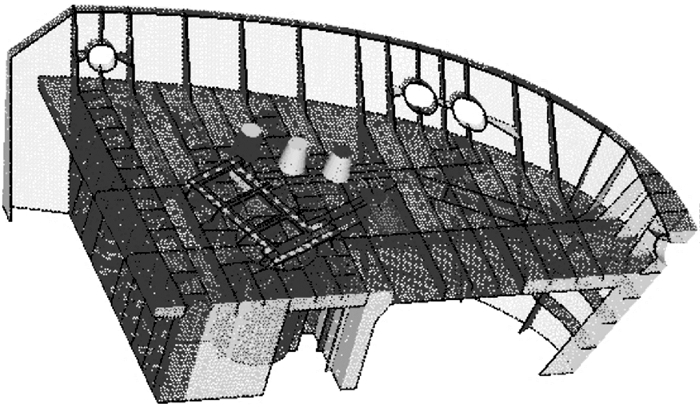
图 7 算例C模型图 Figure 7 Model of Example C |
算例A:节点数是17 524,单元数是8 500;
算例B:节点数是7 690,单元数是718;
算例C:节点数是85 968,单元数是85 832.
本次实验首先将本文改进的算法与邵美悦[25]的基于超节点的不完全LU分解进行比较.本文在相同实验环境下,分别取舍弃阈值(τ)为0.01、0.001和0.000 1来对算法进行对比.
在表 1中可以看出,该算法在计算时间上是有所减少的,并且在舍弃阈值(τ)为0.001时算法可以取得比较好的计算效果.于是,在该算法的并行计算中取该数值.
| 表 1 算法比较 Table 1 Comparison of algorithms |
在与邵美悦的算法进行对比后,接着在广州超级计算先导系统中对并行算法的优化进行测试,采用的例子与前面相同,并且仅以图 5~7中的算例结果进行具体分析.
并行计算中的加速比是用并行前的执行速度和并行后的执行速度之比来表示的,它表示了在并行化之后的效率提升情况,设T1为单处理器计算同一问题所用时间,Tp为p个处理器求解该问题所需时间,加速比为
| 表 2 计算结果 Table 2 The calculation results |
从表 2可以看出,无论是单节点计算或双节点计算,改进的算法都可以减少计算耗时,并且双节点并行计算的时间大大小于串行计算的时间.表 3说明,随着问题规模的增加,算法的加速比是增加的,也就是算法的加速效果呈上升趋,势并且改进后的加速比明显优于并行化改进前.
| 表 3 加速比 Table 3 Speedup ratio |
在广州超算先导系统环境下,对有限元求解器Calculix中预处理迭代方法进行基于列选主元的多行双门槛舍弃策略的并行化改进,提高了并行求解的计算速度,有效降低了船舶设计中有限元分析计算时间.当然,基于列选主元的多行双门槛舍弃改进在预处理时引进动态舍弃策略,预处理时间有所增长,但总体的迭代计算时间仍有所减少,如何进一步降低预处理时间在总体计算时间中的比例将是后续研究的重点.
| [1] |
郭历伦, 陈忠富, 罗景润, 等. 扩展有限元方法及应用综述[J].
力学季刊, 2011, 32(04): 612-625.
Guo L L, Chen Z F, Luo J R, et al. A review of the extended finite element method and its applications[J]. Chinese Quarterly of Mechanis, 2011, 32(04): 612-625. |
| [2] | Dhatt G, Touzot G. Finite Element Method[M]. New York: John Wiley & Sons, 2012. |
| [3] |
李上明. 基于比例边界有限元法动态刚度矩阵的坝库耦合分析方法[J].
工程力学, 2013, 30(02): 313-317.
Li S M. Transient analysis method for dam—reservoir interaction based on dynamic stiffness of SBFEM[J]. Engineering Mechanics, 2013, 30(02): 313-317. |
| [4] | 陈林. 基于Linux机群的大型结构并行有限元方法研究[D]. 南京: 河海大学土木工程学院, 2006. http://cdmd.cnki.com.cn/article/cdmd-10294-2006076844.htm |
| [5] | Dhondt G, Wittig K. Calculix: A Free Software Three-dimensional Structural Finite Element Program, 1998[M]. Boston: Free Software Foundation, 2005. |
| [6] |
魏存祥, 龚建春, 仉洪云. 基于ANSYS的并行计算发展及实现[J].
机械工程师, 2007, 10(2): 95-96.
Wei C X, Gong J C, Zhang H Y. Development and realization of parallel computation based on the ANSYS[J]. Mechanical Engineer, 2007, 10(2): 95-96. |
| [7] |
刘昆, 彭美春, 林怡青, 等. 基于ANSYS Workbench鼓式制动器冲焊蹄的有限元分析[J].
广东工业大学学报, 2013, 30(1): 92-96.
Liu K, Peng M C, Lin Y Q, et al. Finite element analysis of drum brake stamping-welding shoes based on ANSYS workbench[J]. Journal of Guangdong University of Technology, 2013, 30(1): 92-96. |
| [8] | Li G G, Cai G X, Li Y Y. Parallel development of commerce FEA software on SW-I supercomputer[J]. Structural Engineers, 2003, 66(02): 318-323. |
| [9] |
李丽君, 金先龙, 李渊印, 等. 有限元软件结构分析模块的并行开发及应用[J].
上海交通大学学报, 2004, 38(8): 1354-1357.
Li L J, Jin X L, Li Y Y, et al. Parallel development and application of FEA software structural analysis module[J]. Journal of Shanghai Jiaotong University, 2004, 38(8): 1354-1357. |
| [10] | Tinney W F, Walker J W. Direct solutions of sparse network equations by optimally ordered triangular factorization[J]. Proceedings of the IEEE, 1967, 55(1): 1801-1809. |
| [11] | Yousef Saad, Henk A van der Vorst. Iterative solutio of linear systems in the 20th century[J]. Journal of Computational and Applied Mathematics, 2000, 123(1): 1-33. |
| [12] | Hestenes M R, Stiefel E. Methods of conjugate gradients for solving linear systems[J]. Res Nat Bur Standards, 1952, 49(8): 409-436. |
| [13] |
骆志刚, 仲妍, 吴枫. 稀疏线性方程组求解中的预处理技术综述[J].
计算机工程与科学, 2010, 32(12): 89-93.
Luo Z G, Zhong Y, Wu F. Preprocessing techniques for solving sparse linear systems[J]. Computer Engineering & Science, 2010, 32(12): 89-93. |
| [14] |
李晓梅, 吴建平. 稀疏线性方程组不完全分解预条件方法[J].
计算机工程与科学, 2006, 49(08): 59-62.
Li X M, Wu J P. An incomplete decomposition preconditioning method for sparse linear equations[J]. Computer Engineering & Science, 2006, 49(08): 59-62. DOI: 10.3969/j.issn.1007-130X.2006.08.021. |
| [15] | Yousef Saad. ILUT: a dual threshold Incomplete ILU precondition[J]. Numerical Linear Algebra Applications, 1994, 1(4): 387-402. DOI: 10.1002/(ISSN)1099-1506. |
| [16] | Zhao N, Yue T X. Fast methods for solving high accuracy surface modeling[J]. Journal of Algorithms & Computational Technology, 2013, 7(2): 187-196. |
| [17] |
曹方颖, 吕全义, 谢公南. 一类特殊矩阵方程的并行预处理变形共轭梯度算法[J].
应用数学和力学, 2013, 34(3): 240-251.
Cao F Y, Lü Q Y, Xie G N. A parallel precondition modified conjugate gradient method for a kind of matrix equation[J]. Applied Mathematics and Mechanics, 2013, 34(3): 240-251. |
| [18] | Pu Z N, Wang X Z, Lam Hak-Keung. Block preconditioned SSOR methods for H -Matrices linear systems[J]. Journal of Applied Mathematics, 2013, 201(3): 198-203. |
| [19] |
张健飞, 沈德飞. 基于GPU的稀疏线性系统的预条件共轭梯度法[J].
计算机应用, 2013, 33(03): 825-829.
Zhang J F, Shen D F. GPU-based preconditioned conjugate gradient method for solving linear systems[J]. Journal of Computer Applications, 2013, 33(03): 825-829. DOI: 10.3969/j.issn.1001-3695.2013.03.047. |
| [20] | Ail C, Akira N, Satoshi M. Fast conjugate gradients with multiple GPUs[C]// Computational Scinence-ICCS2009, LNCS5544. Berlin: Springe, 2009: 893-903. |
| [21] | 吴建平. 稀疏线性方程组迭代法中的预处理技术研究[D]. 长沙: 国防科技大学计算机学院, 2002. http://cdmd.cnki.com.cn/Article/CDMD-90002-2003097676.htm |
| [22] | 周国标, 宋宝瑞, 谢建利. 数值计算[M]. 北京: 高等教育出版社, 2008: 55-111. |
| [23] | 杨大地, 王开荣. 数值分析[M]. 北京: 北京科学出版社, 2006. |
| [24] |
王握文, 陈明. "天河一号"超级计算机系统研制[J].
国防科技, 2009, 30(6): 2-4.
Wang W W, Chen M. The research and development of the super computer system Tianhe-One[J]. National Defense Science & Technology, 2009, 30(6): 2-4. |
| [25] | 邵美悦. 一种基于超节点的不完全LU分解算法[D]. 上海: 复旦大学数学科学学院, 2009. 一种基于超节点的不完全LU分解算法 |
 2015, Vol. 32
2015, Vol. 32