随着通信及网络技术的发展,无线传感器网络(Wireless Sensor Networks, WSN)近几年在科学界迅速发展,并在军事、医疗、环境监测、目标跟踪等各个领域有着广泛的应用[1-3].WSN是由具有通信和计算能力的无线传感器节点组成的网络系统,通过这些节点来感知被监测区域的环境[3-4].只有在知道节点本身位置信息的情况下,才能保证所获数据的有效性[5-6].所以,定位技术成了WSN中至关重要的技术之一.研究人员依据是否需要测量距离,将各种琳琅满目的WSN定位算法大致分为测距算法和非测距算法[7-8].
典型的测距算法主要有以下4种:基于信号到达时间(Time of Arrival, TOA)、信号到达时间差(Time Difference of Arrival, TDOA)以及基于信号角度(Angle of Arrival, AOA)和信号接收强度(Received Signal Strength Indicator, RSSI)的方法[9-10].AOA算法由于凭借较高的定位精度[11-12],引起了一些研究人员的关注.
本文在研究经典AOA算法的基础上,提出了一种新的定位算法,在只有一个邻居锚节点的条件下,未知节点就能够计算出自身的位置.并且该算法简单,容易实现.
1 经典AOA算法经典AOA算法在每个节点上都配有两个接收机,两个接收机能够根据邻居节点所发送的信号速度以及信号的收发时间确定邻居节点和两个接收机间的距离.
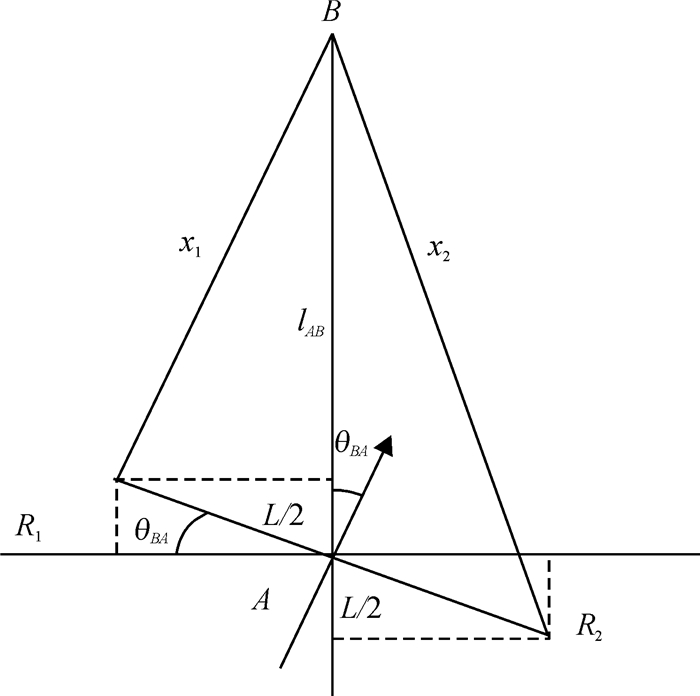
1.1 相邻方位角的测定如图 1所示,节点A有两个接收机R1、R2,L为两个接收机之间的距离.R1、R2连线的中点为节点A的中心位置.经过节点A且与R1、R2连线垂直的线,被定义为点A的基准线,用于确定邻居节点方位角[12].R1、R2接收到节点B发出的信号后,可以计算节点B与两个接收机的之间的距离,分别为x1和x2.根据直角三角形的边和角的关系,节点A可以计算出节点B相对于自己的方位角θBA,如式(1)所示.
| $ \text{sin}{{\mathit{\theta }}_{\mathit{BA}}}\text{=}\frac{\left| {{\mathit{x}}_{\text{1}}}-\text{}{{\mathit{x}}_{\text{2}}} \right|}{\mathit{L}}\text{.} $ | (1) |
|
图 1 节点结构图 Figure 1 The node structure |
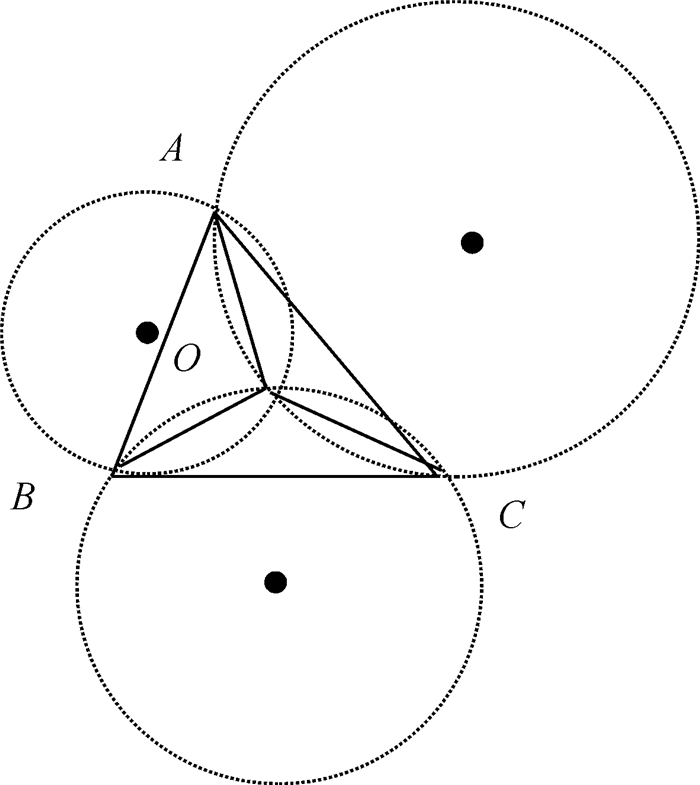
AOA算法的数学原理是:已知一个三角形的3个顶点的坐标,以及该三角形任一内点与其3个顶点之间的夹角,利用圆周角的性质确定三角形内点所在的3个圆,计算3个圆的交点,即为三角形内点.如图 2所示,A、B、C 3点为未知节点O周围的锚节点,节点O在节点A、B、C 3点组成的三角形内.已知∠AOB、∠BOC、∠AOC时,即可计算出图中分别以AB、BC、AC为弦的3个圆的半径,并可以确定3个圆.最后求得未知节点O即为3个圆的交点[13-14].
|
图 2 三角测量法 Figure 2 Triangulation algorithm |
在三角测量法的基础上衍生出了众多基于角度的定位算法.但经典的三角测量法中只有当未知节点周围有3个或者3个以上的锚节点时,才能被比较准确定位.当周围锚节点数小于3个时,无法确定未知节点的位置,会产生定位盲区.
2 改进的AOA算法 2.1 计算节点间的距离在描述算法之前,先假设整个网络时间是同步的.从图 1可以看出,节点A除了能够测得节点B的方位角,同时还能计算出节点A与节点B的距离,假设为lAB.已知x1和x2的值,方位角θ,两个接收机之间的距离L,则两节点之间的距离lAB可以根据直角三角形边和角度之间的关系计算出来.假设X为x1和x2中值较小的一个,则可以求出节点A和节点B之间的距离lAB如式(2)所示,其中lAB≫L.
| $ {{\mathit{l}}_{\mathit{AB}}}\text{=}\sqrt{{{\mathit{X}}^{\text{2}}}-\text{ }\left( \frac{{{\mathit{L}}^{\text{2}}}}{\text{4}} \right)\text{co}{{\text{s}}^{\text{2}}}{{\mathit{\theta }}_{\mathit{BA}}}}\text{+ }\left( \frac{\mathit{L}}{\text{2}} \right)\text{sin}{{\mathit{\theta }}_{\mathit{BA}}}\text{.} $ | (2) |
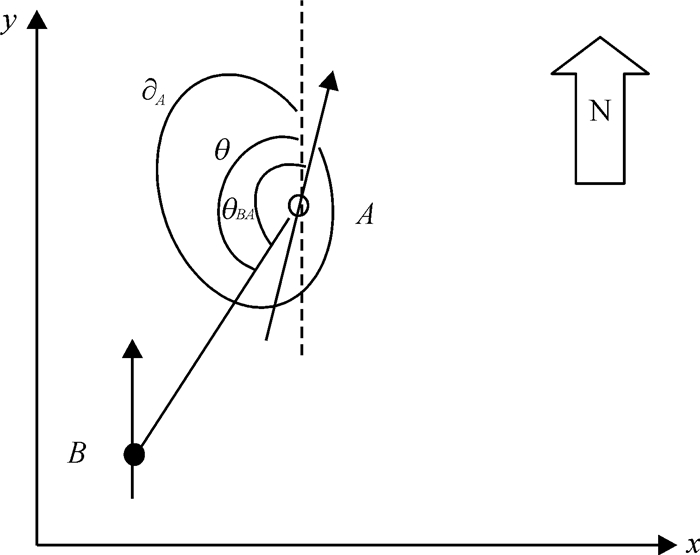
假设每个节点的基准线偏离绝对坐标纵轴角度是已知的.如图 3所示,锚节点B将包含有自身信息的数据发送给节点A,节点A在接收到数据包后,节点B相对于自己基准线的方位角就能够被计算出来,基于以上推导过程,可以计算出节点B和节点A所在直线与绝对坐标系中y轴的偏角如式(3)所示.
| $ \left\{ \begin{align} &\mathit{\theta }\text{=}{{\mathit{\theta }}_{\mathit{BA}}}\text{+}{{\partial }_{\mathit{A}}}\ \text{, }\ \ \text{0}\le {{\mathit{\theta }}_{\mathit{BA}}}\text{+}{{\partial }_{\mathit{A}}}\le \text{2}\pi \text{;} \\ &\mathit{\theta }\text{=}{{\mathit{\theta }}_{\mathit{BA}}}\text{+}{{\partial }_{\mathit{A}}}-\text{2}\pi , \ \ \ \ \text{2}\pi <{{\mathit{\theta }}_{\mathit{BA}}}\text{+}{{\partial }_{\mathit{A}}}\text{.} \\ \end{align} \right. $ | (3) |
|
图 3 节点定位 Figure 3 Node localization |
设(xA,yA)和(xB,yB)分别为节点A和节点B在绝对坐标轴中的位置.则节点B横纵坐标如式(4)所示.
| $ \left\{ \begin{align} &{{\mathit{x}}_{\mathit{A}}}\text{=}{{\mathit{l}}_{\mathit{AB}}}\text{sin}\mathit{\theta }\text{+}{{\mathit{x}}_{\mathit{B}}}\text{;} \\ &{{\mathit{y}}_{\mathit{A}}}\text{=}-{{\mathit{l}}_{\mathit{AB}}}\text{cos}\mathit{\theta }\text{+}{{\mathit{y}}_{\mathit{B}}}\text{.} \\ \end{align} \right. $ | (4) |
由于式(3)中两种情况相差2π,其正弦值、余弦值表达式相同,所以由式(3)和式(4)可得出式(5):
| $ \left\{ \begin{align} &{{\mathit{x}}_{\mathit{A}}}\text{=}{{\mathit{l}}_{\mathit{AB}}}\text{sin}\left( {{\mathit{\theta }}_{\mathit{BA}}}\text{+}{{\partial }_{\mathit{A}}} \right)\text{+}{{\mathit{x}}_{\mathit{B}}}\text{, } \\ &{{\mathit{y}}_{\mathit{A}}}\text{=}-{{\mathit{l}}_{\mathit{AB}}}\text{cos}\left( {{\mathit{\theta }}_{\mathit{BA}}}\text{+}{{\partial }_{\mathit{A}}} \right)\text{+}{{\mathit{y}}_{\mathit{B}}}\text{.} \\ \end{align} \right. $ | (5) |
当节点A周围有n个锚节点B1,B2,…,Bn时,则节点A的坐标为用上述方法所求出来A的坐标的平均值.将定位成功的节点定义为新的锚节点,有效辅助定位其他的未知节点.
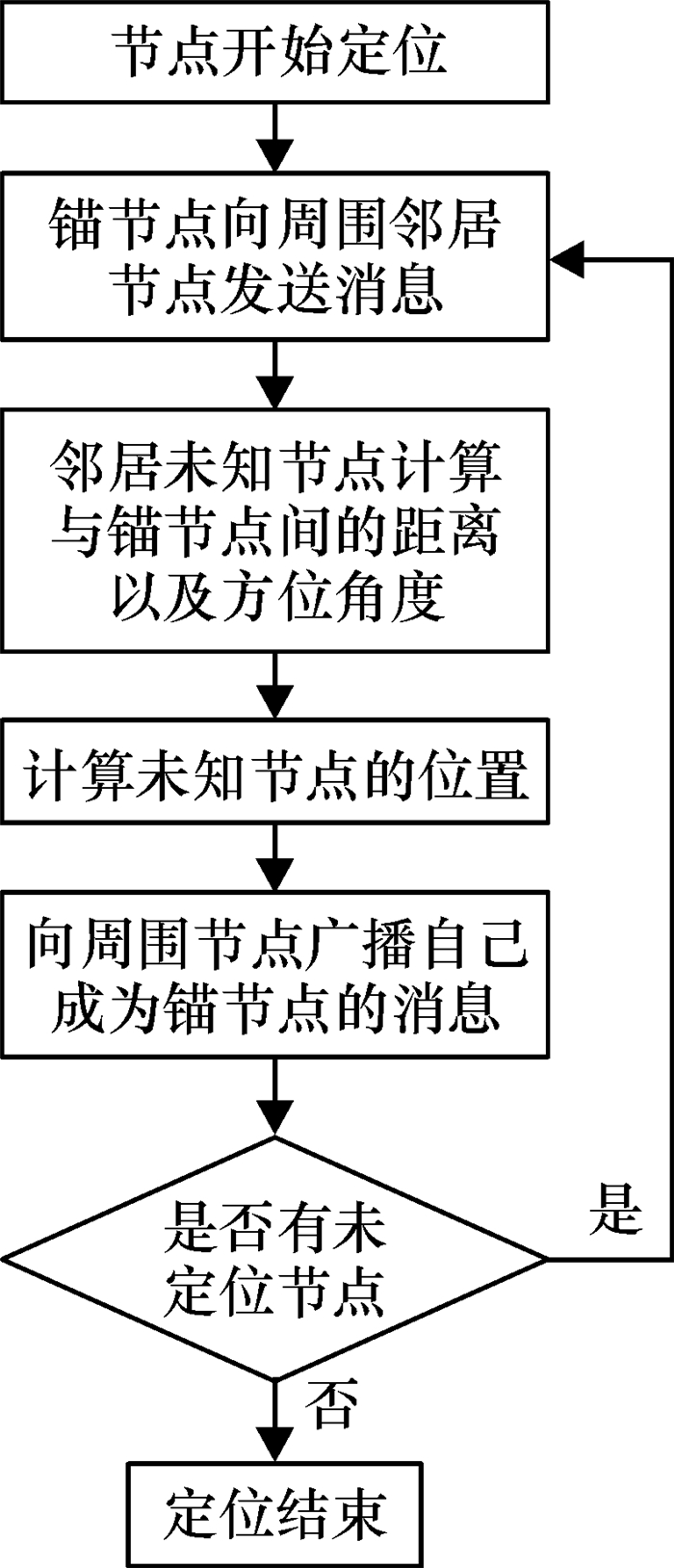
2.3 算法的分析流程图经典AOA算法,未知节点周围至少有3个锚节点时,才能对该未知节点进行定位,不适用于节点稀疏的网络环境.而本文提出的算法只需要计算节点间的距离和节点的方位角,使得未知节点周围只要有一个锚节点就可以实现对该未知节点的定位,可用于解决网络中由于节点稀疏而造成的定位盲区现象,并且本文提出的算法简单且易于实现.算法流程图如图 4所示.
|
图 4 算法流程图 Figure 4 Algorithm flow chart |
本文用Matlab仿真实验,就有效定位率和平均定位误差,对经典AOA算法和本文提出的算法进行了对比分析,在一个大小为5 000 m×5 000 m的区域中随机分布有300个节点,其中有8个锚节点,节点通信半径为400 m.
3.1 有效定位率有效定位率是指已经被正确定位的节点数占整个网络中总节点数的比率[15-17].
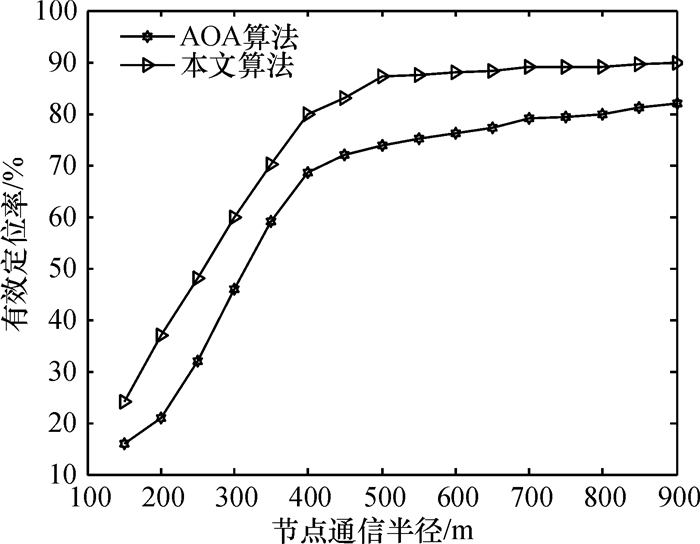
图 5给出了有效定位率随节点通信半径增加的变化趋势,从图中可以看出,当通信半径达到500 m时,本文算法有效定位率达到90%,并趋于稳定,而经典AOA算法在通信半径为700 m时,有效定位率趋于稳定在80%左右.在通信半径相同的情况下,本文算法的定位效果更好.
|
图 5 节点通信半径增加时有效定位率的变化趋势 Figure 5 The trend of effective localization rate with the increase of the node communication radius |
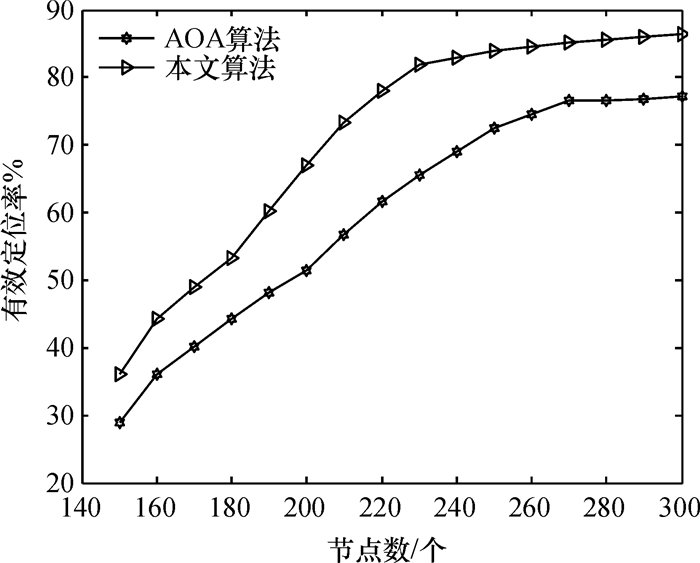
图 6给出了有效定位率随节点增加的变化趋势,从图 6可知,随着总节点数的增加,两种算法定位有效率均不断提高.但当节点个数相同时,本文算法的有效定位率要比经典AOA算法的有效定位率高.从图 6中可以看出,本文提出的算法的有效定位率在85%左右趋于稳定,而经典AOA算法的有效定位率则在75%左右趋于稳定,本文算法的有效定位率明显更高.
|
图 6 节点数量增加时有效定位率的变化趋势 Figure 6 The trend of effective localization rate with the increase of node number |
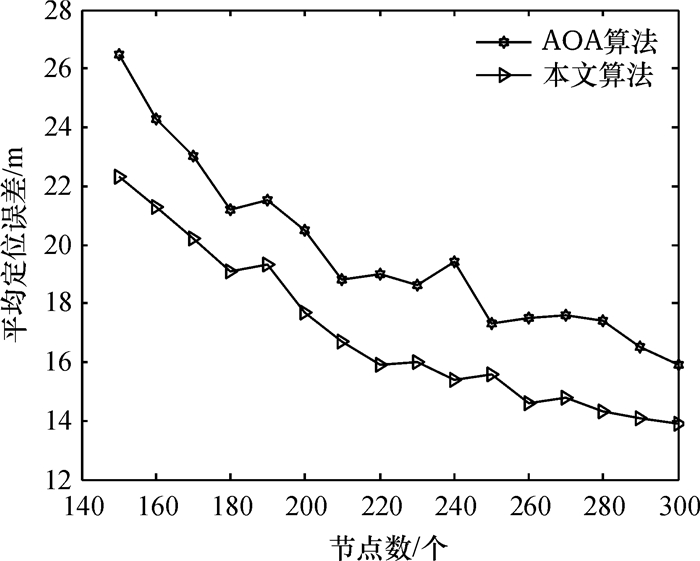
平均定位误差是指利用定位算法计算出的节点的位置所产生的误差的平均值[17].在相同节点数的情况下,本文算法的有效定位率要比经典AOA算法的有效定位率高,并且本文算法的平均定位误差要更低一些,见图 7.图 7中曲线出现了波动现象,是因为节点坐标是自动产生的,导致部分节点有较大的定位误差.
|
图 7 平均定位误差 Figure 7 Average localization errors |
经典AOA算法具有较高的定位精度,但要求未知节点周围至少有3个邻居锚节点才能对其进行定位.本文提出了一种简单且行之有效的自定位算法,未知节点只需要1个邻居锚节点就能够确定自己的位置.能够在未知节点稀疏的情况下实现节点的自定位.仿真实验证明,本文提出的算法精确度比经典AOA算法高,并且有较低的平均误差.
| [1] |
祁荣宾, 李思瑾, 马天义, 等. 基于迭代的无线传感器网络三维定位算法[J].
传感技术学报, 2012, 25(5): 644-650.
Qi R B, Li S J, Ma T Y, et al. Iteration-based localization algorithm for wireless sensor network in three-dimensional space[J]. Chinese Journal of Sensors and Actuators, 2012, 25(5): 644-650. |
| [2] |
王小平, 罗军, 沈昌祥. 无线传感器网络定位理论和算法[J].
计算机研究与发展, 2011, 48(3): 353-363.
Wang X P, Luo J, Shen C X. Theory and algorithms on localization in wireless sensor networks[J]. Journal of Computer Research and Development, 2011, 48(3): 353-363. |
| [3] |
彭越, 吴多龙, Guillaume, 等. 基于最小能量法的无线传感器网络节点能量有效性研究[J].
广东工业大学学报, 2014, 31(1): 86-89.
Peng Yue, Wu D L, Guillaume, et al. Research on Energy-efficiency in Wireless Sensor Networks Based on Minimum Energy Coding[J]. Journal of Guangdong University of Technology, 2014, 31(1): 86-89. |
| [4] |
申柏华, 徐杜. 基于TCP/IP的网络化智能传感器设计[J].
广东工业大学学报, 2005, 22(3): 81-85.
Shen B H, Xu Du. The design of TCP/IP-based intelligent sensor[J]. Journal of Guangdong University of Technology, 2005, 22(3): 81-85. |
| [5] |
王小雪, 吴浩权, 袁荣亮. 无线传感器网络中节点合作定位研究和仿真[J].
电声技术, 2013, 37(9): 69-73.
Wang X X, Wu H Q, Yuan R L. Research and simulation on collaborative positioning in wireless sensor networks[J]. Audio Engieering, 2013, 37(9): 69-73. |
| [6] | Rong Peng, Mihail L. Sichitiu. Angle of Arrival Localization for Wireless Networks[C]//Rong Peng. Sensor and Ad Hoc Communications and Networks. [S. l. ]: [s. n. ], 2006: 374-382. |
| [7] |
彭宇, 王丹. 无线传感器网络定位技术综述[J].
电子测量与仪器学报, 2011, 25(5): 389-399.
Peng Y, W Dan. A review: wireless sensor networks localization[J]. Journal of Electronic Measurement and Instrument, 2011, 25(5): 389-399. |
| [8] |
向满天, 史浩山, 李立宏. 一种基于连通度的无线传感器网络节点定位算法[J].
传感技术学报, 2007, 20(10): 2308-2312.
Xiang M T, Shi H S, Li L H. A node localization algorithm based on connectivity in wireless sensor networks[J]. Chinese Journal of Sensors and Actuators, 2007, 20(10): 2308-2312. DOI: 10.3969/j.issn.1004-1699.2007.10.036. |
| [9] |
王福豹, 史龙, 任丰原. 无线传感器网络中自定位系统和算法[J].
软件学报, 2005, 16(5): 857-868.
Wang F B, Shi L, Ren F Y. Self-localization systems and algorithms for wireless sensor networks[J]. Journal of Software, 2005, 16(5): 857-868. |
| [10] |
周俊奇, 孟庆生. 基于贝叶斯推理的TDOA/AOA定位算法[J].
计算机应用与软件, 2012, 29(6): 233-249.
Zhou J Q, Meng Q S. A bayesian reasoning based TDOA/AOA location algorithm[J]. Computer Applications and Software, 2012, 29(6): 233-249. |
| [11] |
单杭冠, 徐岚, 王宗欣. 基于恒模算法的室内多用户定位技术[J].
复旦学报:自然科学版, 2006, 45(4): 495-500.
Shan H G, Xu L, Wang Z X. Multi-User indoor location technology based on constant modulus algorithm[J]. Journal of Fudan University: Natural science, 2006, 45(4): 495-500. |
| [12] | 孙利民, 李建中, 陈渝, 等. 无线传感器网络[M]. 北京: 清华大学出版社, 2005. |
| [13] |
单志龙, 兰丽. 无线自组织网络中的AOA定位算法[J].
华南师范大学学报:自然科学版, 2009(2): 38-43.
Shan Z L, Lan L. Algorithms of localization using angle of arrival information in ad Hoc networks[J]. Journal of South China Normal University: Natural science edition, 2009(2): 38-43. |
| [14] | Niculescu, D and Badri Nath. Ad Hoc Positioning System (APS) Using AOA[C]// Niculescu, D. Twenty-Second Annual Joint Conference of the IEEE Computer and Communication[S. l. ]: [s. n. ], 2003: 1734-1743. |
| [15] |
蒋鹏, 覃添, 陈岁生. 基于AOA降维和同心圆定位的三维传感器网络节点自定位方法[J].
传感技术学报, 2012, 25(7): 999-1006.
Jiang P, Qin T, Chen S S. AOA and concentric algorithm based three dimensional reduction node self-localization scheme[J]. Chinese Journal of Sensors and Actuators, 2012, 25(7): 999-1006. |
| [16] | Zhou Z, Cui J H, Bagtzoglou A. Scalable localization with mobility prediction for underwater sensor networks[C]// Mobile Computing, IEEE Transaction. [S. l. ]: [s. n. ], 2008: 335-346. |
| [17] |
单志龙, 胡燕. 基于相交环的水下无线传感器网络节点自定位研究[J].
传感技术学报, 2012, 25(4): 536-540.
Shan Z L, Hu Y. Study for the self-localization algorithms based on the intersect rings in underwater wireless sensor networks[J]. Chinese Journal of Sensors and Actuators, 2012, 25(4): 536-540. |
 2015, Vol. 32
2015, Vol. 32