在工程实践中,控制系统模型通常含有多个未知参数,这些参数的慢时变会影响已有控制器的控制效果.为获得优良的控制效果,首先对系统模型进行在线参数辨识,然后再进行控制器设计是自校正控制的基本思想.目前,基于最小二乘辨识法的自校正控制对具有慢时变的参数不确定系统已取得了许多成果[1-3].但是,当被控制对象为高阶系统且受到白色噪声干扰时,常规的基于最小二乘辨识法的自校正控制的控制效果并不理想[4-5].因此,基于神经网络的参数辨识方法得到了发展[6-7].
针对三层BP神经网络算法,文献[8]改进了常规的基于梯度下降法的权值调整算法,即在高斯-牛顿算法的基础上,首先提出了递推预测误差神经网络算法.文献[9]则利用该算法,对含有多个未知参数的系统进行了非线性系统的参数辨识.随后,该方法获得了进一步推广,实现了对高阶的NARMAX模型[10]、多维线性模型[11]、轨道车辆横向振动[12]等系统的参数辨识.但该方法中动量因子与学习率的调整方式会使系统存在收敛慢、辨识精度低等问题.文献[13]针对该算法中的缺陷,在未进行参数辨识的情况下, 引入了动量因子与学习率的优化机制,从而实现了对文献[8]中递推预测误差神经网络算法的改进,系统的稳定性、鲁棒性等性能获得了较好的改善.
本文结合文献[9]和文献[13]中的神经网络,将文献[13]中的改进递推预测误差神经网络算法应用到了非线性系统的模型参数辨识中.而文献[9]和文献[13]均未进行控制器的设计, 考虑到在工程实践中,极点配置PID方法已相对成熟[14-15],故为一类非线性系统设计了基于极点配置的数字PID控制器.
1 系统模型描述考虑如下ARX系统
| $ A\left( {{z^{ - 1}}} \right)y\left( k \right) = {z^{ - d}}B\left( {{z^{ - 1}}} \right)u\left( k \right) + \varepsilon \left( k \right), $ | (1) |
其中,u(k)、y(k)、d、ε(k)依次为系统的输入、输出、纯时延及白噪声干扰;A(z-1)=1+a1z-1+…+anaz-na,B(z-1)=b0+b1z-1+…+bnbz-nb,式(1)还可表示为
| $ y\left( k \right) = \mathit{\boldsymbol{T}}\left( k \right)\mathit{\boldsymbol{Y}} + \varepsilon \left( k \right), $ | (2) |
其中,T(k)=[-y(k-1)…, y(k-na), u(k-d), …u(k-d-nb)],Y=[a1, …ana, b0, …bnb]T.
为在线估计参数向量Y,建立神经网络模型:第1层为输入层,无节点作用函数;第l层(1<l<m)为隐层,节点数记为nl,该层中第i节点的输入、输出、阈值分别记为netil(k)、Oil(k)、bil(k);第l-1隐层中第i节点与第l隐层中第j节点联接权值记为wjil-1(k);第m层为输出层;隐层、输出层节点作用函数记为g(x(k)),动量因子记为αijl、βijl.
输入层的输入、输出为
| $ O_i^1\left( k \right) = {\rm{net}}_i^1\left( k \right) = {T_i}\left( k \right),1 \le i \le {n_1}. $ | (3) |
第l隐层的输入、输出为
| $ {\rm{net}}_j^l\left( k \right) = \sum\limits_{i = 1}^{{n_l} - 1} {w_{ji}^{l - 1}\left( k \right)O_i^{l - 1}\left( k \right)} ,1 \le j \le {n_l}. $ | (4) |
| $ \begin{array}{*{20}{c}} {O_j^l\left( k \right) = g\left( {{\rm{net}}_j^l\left( k \right) + b_j^l\left( k \right)} \right) = }\\ {g\left( {\sum\limits_{i = 1}^{{n_l} - 1} {w_{ij}^l\left( k \right)O_i^{l - 1}\left( k \right)} + b_j^l\left( k \right)} \right),1 \le j \le {n_l}.} \end{array} $ | (5) |
输出层的输出为
| $ O_j^m\left( k \right) = \sum\limits_{i = 1}^{{n_m} - 1} {w_{ji}^{m - 1}\left( k \right)O_i^{m - 1}\left( k \right)} ,1 \le j \le {n_m}, $ | (6) |
节点作用函数为
| $ g\left( {x\left( k \right)} \right) = \frac{1}{{1 + {{\rm{e}}^{ - x\left( k \right)}}}}. $ | (7) |
常规的神经网络各层权值、阈值依据梯度下降法进行调整.
| $ w_{ij}^l\left( k \right) = w_{ij}^l\left( {k - 1} \right) + \alpha _{ij}^l\Delta w_{ij}^l\left( k \right),0 \le \alpha _{ij}^l \le 1, $ | (8) |
| $ b_j^l\left( k \right) = b_j^l\left( {k - 1} \right) + \beta _{ij}^l\Delta b_j^l\left( k \right),0 \le \beta _{ij}^l \le 1. $ | (9) |
选取性能指标函数J(k)为
| $ \begin{array}{l} \ \ \ \ \ \ \ J\left( k \right) = \frac{1}{2}{e^2}\left( k \right) = \frac{1}{2}{\left( {y\left( k \right) - {y_r}\left( k \right)} \right)^2},e\left( k \right) = \\ y\left( k \right) - {y_r}\left( k \right). \end{array} $ | (10) |
在常规神经网络学习算法中,各层权值、阈值依据式(8)~(9)进行调整,以使J(k)最小.但以此方式来训练BP网络,其训练过程容易陷入局部极小值,收敛速度变慢.故本文将改进这种算法.
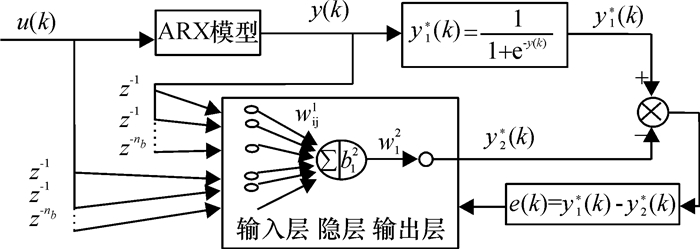
本文采用三层神经网络,即m=3,n2=1,n3=1,建立网络结构如图 1所示.
|
图 1 三层神经网络参数辨识结构 Figure 1 Parameter identification structure of three-layer neural network |
结合式(3)~(7)得
| $ O_i^1\left( k \right) = {\rm{net}}_i^1\left( k \right) = {T_i}\left( k \right),1 \le i \le {n_1}. $ | (11) |
| $ \begin{array}{l} \ \ \ \ \ \ \ y_2^ * \left( k \right) = O_i^3 = w_1^2g\left( {{\rm{net}}_i^2 + b_1^2} \right) = \\ w_1^2g\left( {w_{ij}^1\left( k \right){T_i}\left( k \right) + b_1^2} \right). \end{array} $ | (12) |
由式(12)知网络实际输出y2*(k)与输入Ti(k)为复杂的非线性函数关系;而式(2)中参考输出y(k)与Ti(k)可视为线性关系,故y2*(k)与y(k)变化规律不同.而神经网络实现参数辨识、函数拟合等功能时,要求实际输出与参考输出的变化规律相似,故本文对输出y(k)作畸变处理,以y1*(k)作为参考输出,即
| $ y_1^ * \left( k \right) = g\left( {y\left( k \right)} \right) = \frac{1}{{1 + {{\rm{e}}^{ - y\left( k \right)}}}}. $ | (13) |
针对常规梯度下降法中存在的缺陷,文献[13]利用改进递推预测误差算法对式(8)~(9)中的各层权值、阈值的调整方式作出改进,重新选取性能指标函数
| $ J\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right) = \frac{1}{N}\sum\limits_{k = 1}^N {\mathit{\boldsymbol{E}}_1^T\left( {{\rm{k}},\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right){\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{ - 1}}{\mathit{\boldsymbol{E}}_1}\left( {{\rm{k}},\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right)} . $ | (14) |
其中,N为样本训练数,Λ为nm×nm正定矩阵,结合式(12)~(13)得
| $ {\mathit{\boldsymbol{E}}_1}\left( {{\rm{k}},\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right) = y_2^ * \left( {{\mathit{k}},\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right) - y_1^ * \left( k \right), $ | (15) |
| $ \begin{array}{l} \ \ \ \ \ \ J\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right) = \frac{1}{2}\mathit{\boldsymbol{E}}_1^T\left( {{\rm{k}},\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right){\mathit{\boldsymbol{E}}_1}\left( {{\rm{k}},\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right) = \frac{1}{2}\left( {y_2^ * \left( {{\mathit{k}},\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right) - } \right.\\ {\left. {y_1^ * \left( k \right)} \right)^2}. \end{array} $ | (16) |
其中,Θ(k)为神经网络各层节点间权值和节点阈值构成的向量,即
| $ \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( k \right) = {\left[ {w_{11}^1\left( k \right),w_{21}^1\left( k \right), \cdots w_{{n_1}1}^1,\left( k \right),w_{11}^2\left( k \right),b_1^2}\right]^{\rm{T}}}. $ | (17) |
由高斯-牛顿公式和式(17)得
| $ \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over {\boldsymbol{\varTheta} }} }}\left( k \right) = \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over{ \boldsymbol{\varTheta} }} }}\left( {k - 1} \right) + \mathit{\boldsymbol{K}}\left( k \right)\delta \left( k \right). $ | (18) |
其中,
| $ \mathit{\boldsymbol{K}}\left( k \right) = \mathit{\boldsymbol{Q}}\left( k \right)\mathit{\boldsymbol{f}}\left( k \right), $ | (19) |
| $ \mathit{\boldsymbol{f}}\left( {k,\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right) = \left[ {\frac{{{\rm{d}}y_2^ * \left( {k,\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right)}}{{d\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}}} \right], $ | (20) |
f(k, Θ)为偏导向量,Q(k)为预测误差矩阵,初值取102I~104I,δ(k)的变化规律为
| $ \delta \left( k \right) = {x_m}\left( k \right)\delta \left( {k - 1} \right) + {x_g}\left( k \right)\mathit{\boldsymbol{f}}\left( k \right)\varepsilon \left( k \right). $ | (21) |
其中,xm(k)、xg(k)分别为动量因子、学习率,关系为
| $ {x_m}\left( k \right) = {x_m}\left( {k - 1} \right) + \eta , $ | (22) |
| $ {x_g}\left( k \right) = {x_m}\left( k \right)\left( {1 - {x_m}\left( k \right)} \right). $ | (23) |
| $ \mathit{\boldsymbol{Q}}\left( k \right) = \frac{{\left( {1 - \mathit{\boldsymbol{K}}\left( k \right){\mathit{\boldsymbol{f}}^{\rm{T}}}\left( k \right)} \right)\mathit{\boldsymbol{Q}}\left( {k - 1} \right)}}{{\lambda \left( k \right)}}, $ | (24) |
其中,η为较小常数,实时修正xm(k)值. λ(k)为遗忘因子,0<λ(k)<1,λ(0)为其初值.
| $ \lambda \left( k \right) = \lambda \left( 0 \right)\lambda \left( {k - 1} \right) + 1 - \lambda \left( 0 \right). $ | (25) |
将式(13)代入式(20),得偏导向量f(k, Θ)中元素φ(k)与Θ(k)中元素θ(k)的关系为
| $ \varphi \left( k \right) = \frac{{{\rm{d}}{{\hat y}_1}\left( k \right)}}{{{\rm{d}}\theta \left( k \right)}} = \left\{ {\begin{array}{*{20}{c}} {O_j^2\left( k \right),}&{当\;\theta \left( k \right) = w_1^2\left( k \right)\;时;}\\ {O_j^2\left( k \right)\left( {1 - O_j^2\left( k \right)} \right)w_j^2\left( k \right)O_j^1\left( k \right),}&{当\;\theta \left( k \right) = w_{ij}^1\left( k \right)\;时;}\\ {O_j^2\left( k \right)\left( {1 - O_j^2\left( k \right)} \right)w_j^2\left( k \right),}&{当\;\theta \left( k \right) = b_1^2\left( k \right)\;时;}\\ {0,}&{其他.} \end{array}} \right. $ | (26) |
综上所述,对比式(2)、(13)、(14),知输入层与隐层间的联接权值为待估的模型参数,即
| $ \begin{array}{l} \ \ \ \ \ \ \mathit{\boldsymbol{\hat Y}}\left( k \right) = {\left[ {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_1},{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_2}, \cdots {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_{{n_a}}},{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over b} }_1},{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over b} }_2}, \cdots {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over b} }_{{n_b}}}} \right]^{\rm{T}}} = \\ {\left[ {w_{11}^1\left( k \right),w_{21}^1\left( k \right), \cdots w_{{n_1}1}^1,\left( k \right)} \right]^{\rm{T}}}. \end{array} $ | (27) |
模型(1)的参数确定后,下一步依据极点配置PID方法进行控制器设计.增量式PID控制器[16]为
| $ \begin{array}{l} \ \ \ \ \ \ F\left( {{z^{ - 1}}} \right)\Delta u\left( k \right) = F\left( {{z^{ - 1}}} \right)\left[ {u\left( k \right) - u\left( {k - 1} \right)} \right] = \\ {g_0}e\left( k \right) + {g_1}e\left( {k - 1} \right) + {g_2}e\left( {k - 2} \right). \end{array} $ | (28) |
其中,G(z-1)=g0+g1z-1+g2z-2,F(z-1)=(1-f1z-1)(1-f2z-1)…(1-fnfz-1),e(k)=
| $ \begin{array}{l} \ \ \ \ \ \ A\left( {{z^{ - 1}}} \right)\left( {1 - {z^{ - 1}}} \right)F\left( {{z^{ - 1}}} \right) + {z^{ - d}}B\left( {{z^{ - 1}}} \right)G\left( {{z^{ - 1}}} \right) = \\ {A_0}\left( {{z^{ - 1}}} \right){A_m}\left( {{z^{ - 1}}} \right). \end{array} $ | (29) |
其中,Am(z-1)=1+am1z-1+…+amnaz-nma为闭环期望多项式, A0(z-1)为可调算子多项式.
将式(28)改写为
| $ U\left( z \right) = - \frac{{G\left( {{z^{ - 1}}} \right)}}{{\left( {1 - {z^{ - 1}}} \right)F\left( {{z^{ - 1}}} \right)}}E\left( {{z^{ - 1}}} \right). $ | (30) |
将式(30)代入式(1)得闭环系统输出
| $ \begin{array}{l} \mathit{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}}\left( \mathit{k} \right)=\\ \frac{{{z^{ - d}}B\left( {{z^{ - 1}}} \right)G\left( {{z^{ - 1}}} \right)}}{{A\left( {{z^{ - 1}}} \right)\left( {1 - {z^{ - 1}}} \right)F\left( {{z^{ - 1}}} \right) + {z^{ - d}}B\left( {{z^{ - 1}}} \right)G\left( {{z^{ - 1}}} \right)}}{y_m}\left( k \right) + \\ \frac{{\left( {1 - {z^{ - 1}}} \right)F\left( {{z^{ - 1}}} \right)}}{{A\left( {{z^{ - 1}}} \right)\left( {1 - {z^{ - 1}}} \right)F\left( {{z^{ - 1}}} \right) + {z^{ - d}}B\left( {{z^{ - 1}}} \right)G\left( {{z^{ - 1}}} \right)}}\varepsilon \left( k \right). \end{array} $ | (31) |
选取他激式直流电机调速系统作为被控对象[17]:
| $ \begin{array}{l} \ \ \ \ \ \ \ G\left( s \right) = \frac{{y\left( s \right)}}{{u\left( s \right)}} = \frac{{U\left( s \right)}}{{N\left( s \right)}} = \frac{{\frac{1}{{{C_e}}}}}{{{T_d}{T_m}{s^2} + {T_m}s + 1}} = \\ \frac{c}{{{s^2} + as + b}}. \end{array} $ | (32) |
其中,
| 表 1 电机调速系统技术参数 Table 1 Parameters of motor speed control system |
利用向后差分法对式(32)进行离散化,则直流电机数学模型(32)表示为
| $ \begin{array}{l} \ \ \ \ \ \ \ y\left( k \right) = {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_1}y\left( {k - 1} \right) + {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_2}y\left( {k - 2} \right) + {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_3}y\left( {k - 3} \right)\\ + {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over b} }_1}u\left( k \right) - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over b} }_2}u\left( {k - 1} \right). \end{array} $ | (33) |
其中,
根据表 1和模型(32),得模型(33)各参数的真值为
| $ \begin{array}{l} \ \ \ \ \ \ {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_1} = 1.656\;7,{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_2} = - 0.686\;6,{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_3} = 0.029\;9,{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over b} }_1}\\ = 0.908\;4,{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over b} }_2} = 0.908\;4. \end{array} $ | (34) |
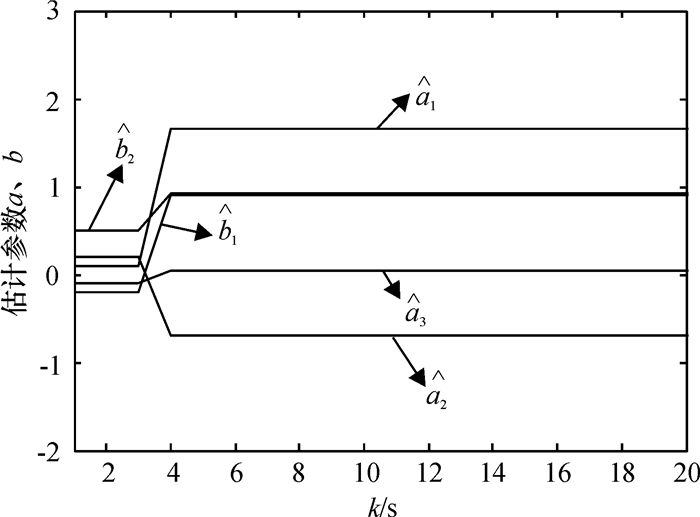
取T=0.5、τ=0.45,λ(0)=0.95、η=1×10-6,Q(0)=5 600,xm(0)=0.98,b12=0.2,u(k)=2sin2πk.施加幅值为1的白噪声干扰,对模型(33)进行参数辨识,则各参数调整过程及误差情况如图 2、3所示。
|
图 2 各估计参数调整过程 Figure 2 Adjustment process of the parameters identification |
|
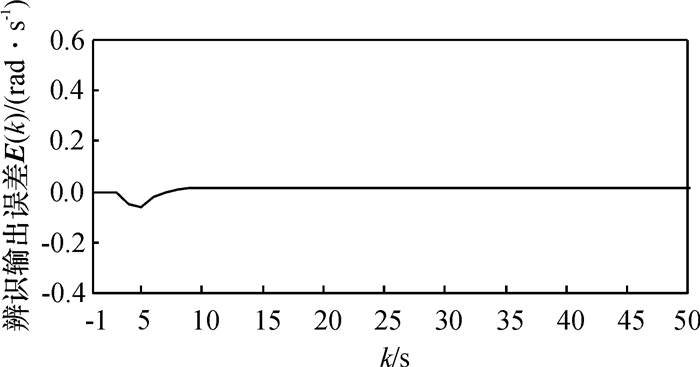
图 3 辨识结构输出、参考输出误差 Figure 3 Error of the actual output and the reference output |
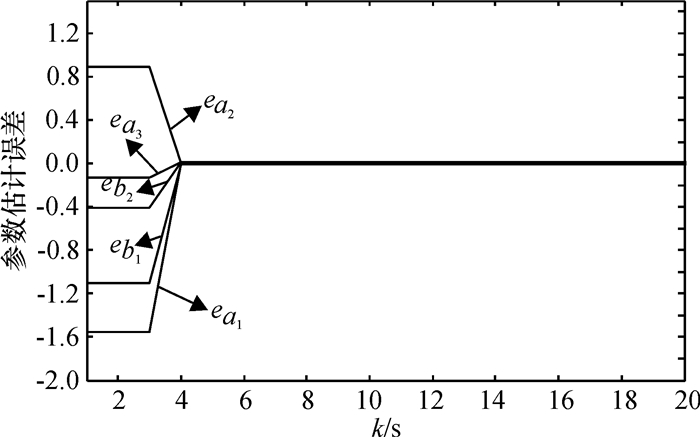
图 2给出了系统各估计参数的调整过程,可看出,各估计参数出现小幅波动后,快速进入收敛稳定状态,对应的各估计参数的估计误差曲线如图 4所示.
|
图 4 各系统参数的估计误差 Figure 4 Estimated error of each system parameter |
图 3为实际输出y2*(k)与参考输出y1*(k)的误差E(k)情况,可看出,E(k)趋向于0;结合式(34)中参数的真值,参考图 4中参数误差,表明了该辨识方法具有精度较高、稳定性好、收敛速度较快的特点.
为证实极点配置PID控制器具有较好的控制效果,引入常规的增量型PID控制器进行比较[18].取Am=1+0.9z-1+0.2z-2, ym=10sin(2πk/50)+5cos (2πk/120)+1.并由Diophantine方程得F(z-1)=(1-z-1)F(z-1) =0.046 422(1-z-1),G(z-1)=1.049 5-0.024 969z-1+0.037 24z-2.为让系统获得更好的跟踪效果,在控制器的前向通道串入两低通滤波器:
|
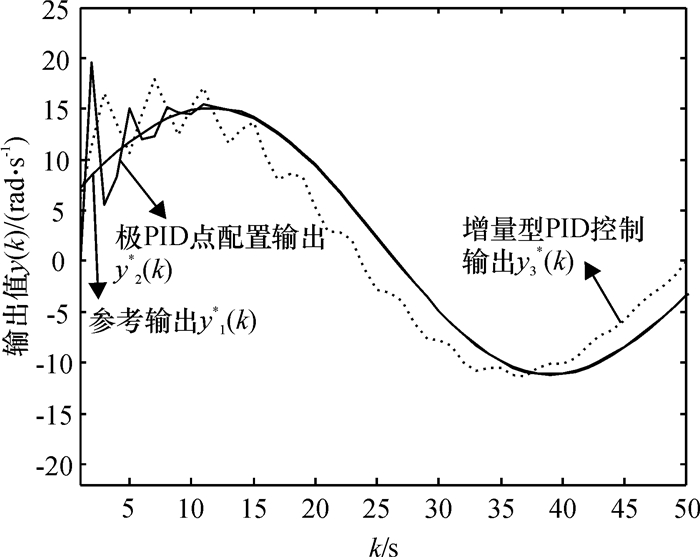
图 5 无白噪声干扰跟踪过程比较 Figure 5 Comparison of tracking processes without white noise interference |
|
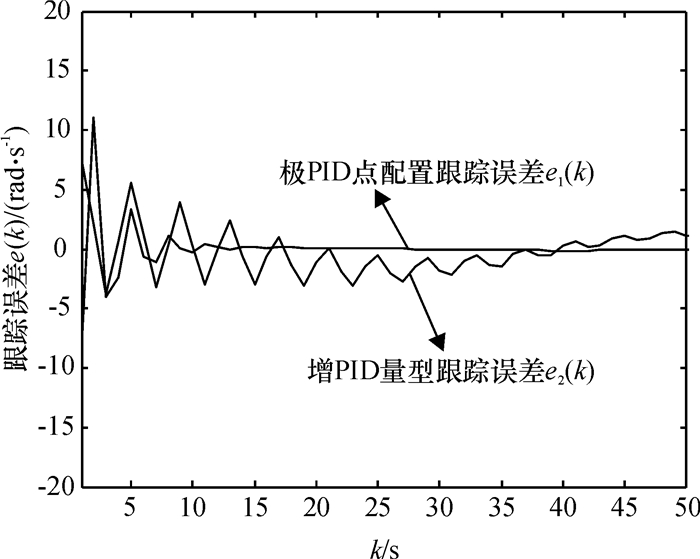
图 6 无白噪声干扰跟踪误差比较 Figure 6 Comparison of tracking errors without white noise interference |
|
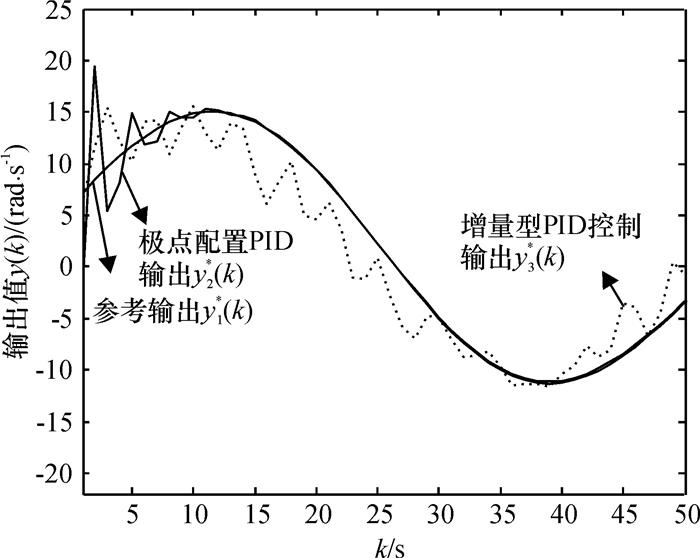
图 7 白噪声干扰跟踪过程比较 Figure 7 Comparison of tracking processes with white noise interference |
|
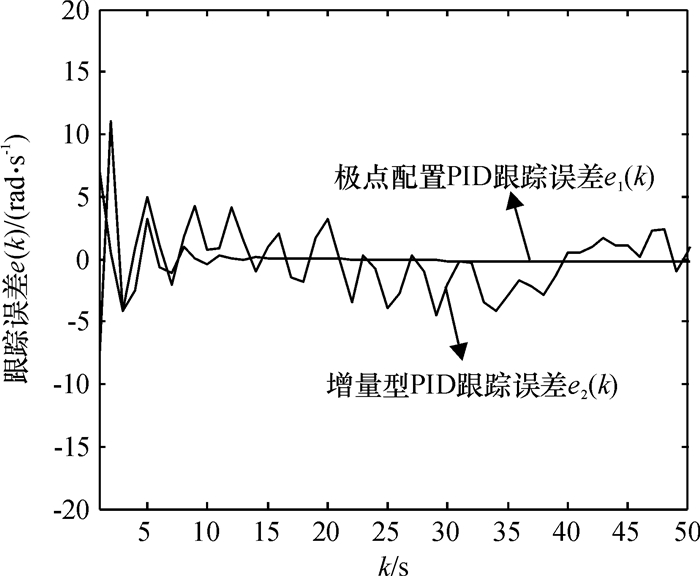
图 8 白噪声干扰跟踪误差比较 Figure 8 Comparison of tracking errors with white noise interference |
图 5、6给出了在无干扰的情形下,利用极点配置PID自校正控制器方法所实现的系统实际输出
本文采用了改进递归预测算法的神经网络控制方法来进行系统参数辨识,在此基础上进行了极点配置PID数字控制器设计.仿真实验以他激式直流电机调速系统模型为例,表明了改进递推预测误差的神经网络算法具有较好的学习收敛速度及辨识精度.另一方面, 本文使用了扩展型极点配置PID自校正数字控制器,由于控制设计过程中PID参数由Diophantine方程确定,所以系统闭环控制过程中参数辨识和PID控制器参数选择更容易实现连续在线调整,这种方法有助方程于工程实践应用.
| [1] |
李开霞, 张金波, 曹爱华. 一种实用的自校正PID控制器的设计与仿真研究[J].
计算机仿真, 2008, 25(9): 167-170.
Li K X, Zhang J B, Cao A H. Design and simulation of an useful self-tuning PID controller[J]. Computer Simulation, 2008, 25(9): 167-170. |
| [2] |
周敏, 刘国海. 基于极点配置算法的温度自校正控制器[J].
微计算机信息, 2008, 24(4): 31-33.
Zhou M, Liu G H. Self-tuning controller of temperature based on pole placement algorithm[J]. Microcomputer Information, 2008, 24(4): 31-33. |
| [3] |
王鸿山, 张兴, 杨淑英, 等. 基于最小二乘法在线参数辨识的异步电动机矢量控制仿真[J].
合肥工业大学学报, 2009, 32(4): 495-499.
Wang H S, Zhang X, Yang S Y, et al. Simulation of the vector control system of induction machines based on least-squares on-line parameter identification[J]. Journal of Hefei University of Technology, 2009, 32(4): 495-499. |
| [4] |
秦来安, 侯再红, 吴毅. 光电跟踪架传递函数辨识方法及应用[J].
红外与激光工程, 2012, 41(10): 2810-2816.
Qin L A, Hou Z H, Wu Y. Transfer function identification method and its application in photoelectrical tracking system[J]. Infrared and Laser Engineering, 2012, 41(10): 2810-2816. DOI: 10.3969/j.issn.1007-2276.2012.10.048. |
| [5] |
童余德, 周永余, 陈永冰, 等. 基于MATLAB的卡尔曼滤波法参数辨识与仿真[J].
船电技术, 2009, 29(8): 47-50.
Tong Y D, Zhou Y Y, Chen Y B, et al. Kalman filter parameter identification and emulate Based on matlab[J]. Marine Electric & Electronic Engineering, 2009, 29(8): 47-50. |
| [6] |
张彪, 赵克定, 孙丰迎. 电液负载模拟器的神经网络参数辨识[J].
航空学报, 2009, 30(2): 374-379.
Zhang B, Zhao K D, Sun F Y. Neural network parameter identification of electro-hydraulic load simulator[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(2): 374-379. |
| [7] |
黎波, 严骏, 郭刚, 等. 基于DRNN神经网络的挖掘机伺服系统参数辨识[J].
解放军理工大学学报, 2013, 14(1): 75-78.
Li B, Yan J, Guo G, et al. Parameter identification of servo system for excavator based on DRNN[J]. Journal of PLA University Science and Technology, 2013, 14(1): 75-78. |
| [8] | Chen S, Billings S A. Neural networks for nonlinear dynamic system modelling and identification[J]. International Journal of Control, 1992, 56(2): 319-346. DOI: 10.1080/00207179208934317. |
| [9] |
董德存, 张树京. 用于AR参数估计的一种神经网络新方法[J].
北方交通大学学报, 1994, 18(2): 167-171.
Dong D C, Zhang S J. New method of AR parameters estimation using neural network[J]. Journal of Northern Jiao-tong University, 1994, 18(2): 167-171. |
| [10] |
董德存, 张树京. 用于NARMAX参数辨识的一种神经网络方法[J].
铁道学报, 1994, 16(2): 53-56.
Dong D C, Zhang S J. A method of neural network for NARMAX parameters identification[J]. Journal of the China Railway Society, 1994, 16(2): 53-56. |
| [11] |
董德存, 张树京. 多维线性模型参数估计的神经网络方法[J].
振动与冲击, 1996, 15(2): 75-80.
Dong D C, Zhang S J. Neural networks for parameter estimation of multi-dimension linear model[J]. Journal of Vibration and Shock, 1996, 15(2): 75-80. |
| [12] |
张亚林, 胡用生, 董德存, 等. 基于神经网络的轨道车辆横向振动模型辨识[J].
城市轨道交通研究, 2002, 2: 3-36.
Zhang Y L, Hu Y S, Dong D C, et al. Identification of lateral vibration model for vehicle on the neural network[J]. Urban Mass Transit, 2002, 2: 3-36. |
| [13] | Mashor M Y. Performance comparison between HMLP, MLP and RBF networks with application to online system identification[C]// Cybernetics and Intelligent Systems, 2004 IEE Conference on: IEEE, 2004, 1: 643-648. |
| [14] | Richardson R, Brownb M, Bhaktac B, et al. Impedance control for a pneumatic robot-based around pole-placement, joint space controllers[J]. Control Engineering Practice, 2005, 13(3): 291-303. DOI: 10.1016/j.conengprac.2004.03.011. |
| [15] |
陈青昌, 彭力, 康勇. 基于极点配置的DC/DC变换器PID参数优化设计[J].
通信电源技术, 2005, 22(2): 6-13.
Cheng Q C, Peng L, Kang Y. PID controller parameters' optimization for DC/DC converters based on pole deploying[J]. Telecom Power Technologies, 2005, 22(2): 6-13. |
| [16] | 徐湘元. 自适应控制理论与应用[M]. 北京: 电子工业出版社, 2007. |
| [17] | 王忠礼, 段慧达, 高玉峰. MATLAB应用技术-在电气工程与自动化专业中的应用[M]. 北京: 清华大学出版社, 2007. |
| [18] | 庞中华, 崔红. 系统辨识与自适应控制MATLAB仿真[M]. 北京: 北京航空航天大学出版社, 2009. |
 2015, Vol. 32
2015, Vol. 32