2. 深圳大学 经济学院,广东 深圳 518060
2. College of Economics, Shenzhen University, Shenzhen 518060, China
生产物流是指在企业内部围绕生产而进行的物流活动,它包括了原材料购进、车间生产、半成品与成品周转等生产过程中所产生的仓储、包装、运输等一系列物流活动.生产物流活动不仅是贯穿在企业整个生产过程中的物流活动,同时也衔接着企业生产与销售物流,因此其效率的高低对企业生产、销售物流都有显著的影响[1].相对于社会物流而言,生产物流过程在整个生产过程中所占的比重最高可达95%,而且生产物流运作紧凑,生产物流过程的低效率会对生产物流过程乃至生产效率产生很大的影响[2].为了保障生产物流过程流畅高效地运作,就需要对生产物流运输资源进行合理配置和调度.
目前关于资源调度的研究已取得颇为丰富的成果[3-5],但对生产物流运输资源进行配置的研究则相对较少.有学者在研究企业内各车间之间物料搬运方式配置问题时,在保证满足任意两站点之间流量需求和任意车间之间对运输方式约束的条件下,建立以配置总成本最小为优化目标的0-1整数规划模型[6].文献[7]在考虑运输设备满足各类货物作业量需求、各吨位对运输设备限制、最长工作时间约束前提下,以最小成本为目标,建立运输资源的配置模型.文献[8]在考虑服务时间与距离条件下,提出了一种优先权规则调度算法,并基于排队论模拟仿真车间吊车调度系统.文献[9]研究了生产线上运输资源形成的两环闭型排队网络模型,在考虑系统随机性条件下, 构建了问题模型, 并提出重叠式分解迭代解析算法.文献[10]在配置钢铁物流园区运输资源时,在考虑满足任务需求、资源利用率、任务对资源约束的情况下,建立目标为最小运营成本和最大总作业能力的多目标优化模型.
然而,目前学者们对于生产物流运输资源配置的研究,虽有考虑作业量需求、工作时长、运作效率、设备替换性等因素的约束[7, 10-11],但未能充分考虑作业过程中物流运输需求的动态性和不确定性所带来的影响; 或者考虑了物流运输需求的动态性及不确定性影响,但仅对平均等待时间、系统产率等指标进行优化[8-9],却未能考虑物流运输资源配置成本、资源可替换性、工作时长约束的影响.对于考虑生产物流运输需求具有显著动态性和不确定性,物流运输资源具有可替换性及工作时长约束的物流运输资源优化配置问题的研究,笔者目前还未见有研究报道.在按单生产模式下,产品从车间生产线下线开始到存放至仓库(成品入库),这一生产物流局部过程具有显著动态性和不确定性,同时对运输资源也有限制要求.成品入库作为生产物流的末尾环节,是衔接生产与发货的桥梁,其运作状况的优劣直接影响发货乃至生产过程流畅性和效率.因此,有必要对这一过程中的物流运输资源配置问题进行研究.
本文选择对生产物流管理要求尤其严格的化工生产企业为研究对象,在采用按单生产的模式下,分析生产物流过程的末尾环节——成品入库过程的动态性和不确定性,研究在考虑物流运输需求具有动态性和不确定性、资源可替换性、工作时长约束下的生产物流运输资源优化配置问题.尽管本文选择了化工生产企业为研究对象,考虑了生产物流需求对物流运输资源的限制要求及运输资源的可替换性,但其研究思路及结果也适应于其他类对动态性生产物流具有严格管理要求的制造企业.
1 问题描述某大型化工企业的生产主要采用按单生产模式,其“生产-物流”运作流程如图 1所示.各车间成品下线后被摆放至托盘,在车间临时存放,由两种叉车(内燃叉车和电动叉车)完成这些产品的入库任务.为了方便管理与发货配送,所有的订单都按一定的规则被预先分配到不同的仓库.在成品下线时,车间工人根据产品订单将去往不同仓库的产品分别摆放在不同的托盘上,以方便叉车一次性将产品运输入库.叉车在车间取托盘后,将托盘运送至对应的目标仓库,并摆放至预先为订单分配的货道上.
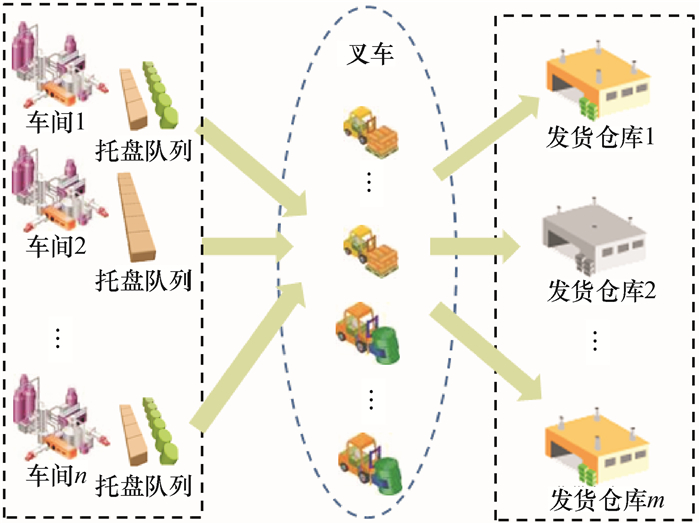
|
图 1 某企业“生产-物流”运作流程 Figure 1 Production and logistics operation process of an enterprise |
在此过程中,根据运输产品的不同,对所选用的叉车也有一定的要求:车间生产的甲类产品只能进入可存放甲类产品的仓库,由于甲类产品属于易燃易爆化学品,运输过程中必须使用内燃叉车运输; 根据产品在托盘上摆放产品的质量,将入库托盘又分为轻重两类,对应吨位较大的托盘(2 t以上)也只能使用内燃叉车运输; 电动叉车和内燃叉车可相互替换完成其他类产品托盘的入库任务.
在按单生产模式下,由于订单需求的多样性和随机性,上述“生产-物流”运作过程往往受到多种动态性、不确定性因素的影响,造成物流运作过程的不稳定.
(1) 企业内车间和仓库众多,同时各车间生产产品的数量有很大不确定性,而各车间生产的产品(以托盘为单位)的目标仓库也具有很大的不确定性,造成了各车间产品入库对运输资源需求在路径分布上的不确定性;
(2) 各车间生产的产品种类经常变化,而不同产品的生产流程工序会引起各车间生产产品周期的不确定,造成各车间对物流运输需求在时间分布上的不确定性;
(3) 在1年中,企业内的成品入库物流运输需求以每个季度为1个大的波动周期,而在每个季度里,又以每个月为1个小波动周期,物流运输需求具有很大的随机动态性.
除去上述动态性和不确定性因素外,由于企业采用的是按单生产模式,产品的交付有着严格的时间要求,延迟交付企业要根据延迟程度支付相应的延迟罚金,因而成品入库物流运作也有着严格的时间要求.
综上所述,对上述物流过程中的运输资源优化配置必须考虑物流运输需求的动态性和不确定性、运输任务对运输资源的限制、运输资源的可替换性、物流延迟所带来的损失.通过上述分析可知,成品入库过程是一个随机服务过程,而排队论是研究随机服务系统的理论,广泛应用于各领域随机服务系统的优化问题.本文将基于排队论,在“生产-物流”运输需求具有动态性和不确定性、物流运输资源可替换的条件下,研究成品入库过程中的运输资源配置问题,提出一种物流运输资源的优化配置方法.
2 数学模型及求解 2.1 资源配置问题运输资源配置问题是一个实际工程问题,由于实际工程中运输需求存在动态性的特点,可将研究时间范围H内的资源配置问题根据需求变化的特点划分为若干个时间段进行配置研究.参照文献[12],对多种资源配置问题可描述为
| $ R = \left\{ {\left( {{\delta _i},{s_i}} \right):{s_i} \in I} \right\}, $ | (1) |
其中,δi表示第i种资源类型,I为资源类型集合,si为第i种资源的配置数量.
在每个时间段θ中,运输资源的配置可描述为
| $ R\left( \theta \right) = \left( {{R_\theta },\theta } \right), $ | (2) |
Rθ为在时间段θ期间运输资源的配置.
而整个研究期间H内的运输资源配置P可描述为
| $ P = \left\{ {R\left( \theta \right):\theta \in H} \right\}. $ | (3) |
叉车运送成品入库过程是一个随机服务过程,而排队论正是研究随机服务系统的理论,近年来排队论在资源配置方面的研究应用领域越来越多.文献[13]利用排队论研究了成品仓出入库任务随机到达,服务时间不确定的天车数量配置问题.文献[14]在研究矿山排土车辆配置问题时,在考虑排土点随机分布、服务时间服从负指数分布的条件下,基于排队论提出了一套优化配置方法.文献[15]基于开排队网络理论提出了生产线资源的优化配置方法.
综上所述,排队论往往应用于任务到达具有随机性、不确定性以及服务时间不确定的服务系统,而本文研究的成品入库过程中,叉车运送产品入库的目标仓库也具有随机性和不确定性,服务时间也是不确定的.因此,本文尝试使用排队论模型解决物流运输资源(叉车)的配置问题.
参考相关资料[16],M/M/s排队模型的描述如下:设物流系统中有s辆运输车辆,并且各车辆的工作相互独立; 运输任务按泊松流到达,到达强度为λ,期望到达间隔为1/ λ; 每辆车任务运输时间为负指数分布,平均服务率为μ,期望服务时间为1/ μ; 整个系统的平均服务率为sμ; 系统服务强度
| $ {W_s} = \frac{{{s^s}{\rho ^s}{p_0}}}{{s!{{\left( {s - \rho } \right)}^2}\mu s}} + \frac{1}{\mu }, $ | (4) |
其中,
在未考虑系统不确定性和动态性的情况下,优化配置模型[7, 10-11, 17]中系统运营成本仅包含资源的采购成本、燃油动力成本、维修保养成本.为对物流运输系统中动态性和不确定性带来的影响进行准确的评估,本文选择物流系统的平均入库等待时间为评价指标; 同时由于在实际的系统运行中运输延时往往会给企业带来损失,因此将由物流系统的平均等待时间延迟带来的损失加入物流系统的运营成本中.
为了使建立的排队模型不因过于复杂而造成求解困难,同时又保障所建模型与企业实际生产物流运作过程相符合,先对所要建立的模型做一些必要的假设.将所有车间产品入库任务看作是两条队列,其中一条由重量较轻且不能存放入甲类产品仓库入库任务组成,另一条由甲类产品或重量较重的产品入库任务组成.假设这两条队列的入库任务到达过程为泊松流,到达率为 λk; 排队规则为先到先服务的等待制,系统容量看作为无限; 电动叉车只服务其中重量较轻且不能存放入甲类产品仓库的任务队列,内燃叉车服务甲类产品和重量较重的产品入库任务,此外也可替换电动叉车完成非甲类产品的入库任务.
考虑到物流运输需求的全年动态性变化显著的特点,本模型将根据各月物流运输需求对各月的系统运营成本进行计算.以系统的年运行成本G为优化目标,构建如下数学模型
| $ \min G = \sum\nolimits_i {\sum\nolimits_k {{G_{ik}}} } , $ | (5) |
式(5)中:
| $ {G_{ik}} = {P_{ik}} + {R_{ik}} + {W_{ik}}, $ | (6) |
| $ {P_{ik}} = {p_k}{s_k}{d_i}{C_k}, $ | (7) |
| $ {R_{ik}} = \frac{{{\lambda _{ik}}{r_k}{d_i}}}{{{\mu _k}}}, $ | (8) |
| $ \begin{array}{l} {W_{ik}} = \left\{ \begin{array}{l} {\lambda _{ik}}{d_i}\left( {{W_{ks}} - {W_a}} \right){C_w},{W_{ks}} > {W_a},\\ 0,{W_{ks}} \le {W_a}. \end{array} \right.\\ {\rm{s}}.\;\;{\rm{t}}. \end{array} $ | (9) |
| $ {W_{ks}}{\mu _k} \le {d_a}, $ | (10) |
| $ {\lambda _{ik}} \ge {\lambda _{ka}}, $ | (11) |
| $ {\lambda _i} = \sum\nolimits_k {{\lambda _{ik}}} , $ | (12) |
| $ {s_k}、{\lambda _{ik}}为整数, $ | (13) |
符号意义说明如下:
Gik:k型车i月运营成本;
Pik:k型车i月的折旧成本;
Rik:k型车i月的动力成本;
Wik:k型车i月造成的损失成本;
pk:k型车每天的折旧率;
sk:k型车的配置数量;
di:i月工作天数;
Ck:k型车的购置及总维修成本;
λik:k型车在i月每天的任务到达率;
λi:在i月每天任务的总到达率;
μk:k型车在每天的服务率;
rk:k型车单位时间动力成本;
Wks:k型车任务队列产品的平均入库时间(从入库任务产生到产品入库为止);
Wa:产品入库无延迟损失的平均入库时间上限;
da:每天工作时间上限;
Cw:单位时间的延误损失成本.
其中Wks可用式(4)进行计算.
式(6)表示系统的各月运营成本,由购置及全部维修的折算成本、动力成本、延时损失成本构成; 式(7)~(9)分别表示购置及全部维修的折算成本、动力成本、延时损失成本的计算方法,式(10)表示入库服务的工作时间限制约束; 式(11)表示两类叉车必须单独完成的入库任务量,特别是内燃叉车必须完成甲类产品及重托盘的入库任务,任务量用任务到达率表示; 式(12)表示电动叉车和内燃叉车的总入库任务量.式(11)、(12)保障了入库任务能够被完成,同时也可对入库任务进行相应的分配,解决了叉车资源的可替换性问题.对于模型的求解,可采用标准的遗传算法进行求解,这里不再赘述.
3 案例分析本文研究某化工企业的成品入库物流过程,该企业内有5个车间,3个成品仓库.其中,1、4号车间生产甲类、乙类产品,2、3、5号车间生产乙类、丙类产品; 6号仓库是只能存放甲类产品的成品仓库,7、8号仓库是可存放非甲类产品的成品仓库,不存放甲类产品.各个车间产品摆放托盘的吨位一般根据产品种类而定,但轻重托盘的比例有一定的波动范围.企业现有两种叉车可供选择,具体参数如表 1所示.由于企业生产各月份具有较大波动性,计算时需考虑各个月份的运输需求,历史数据可得各月份平均每天总入库任务数及必须由内燃叉车入库任务下限(由甲类产品和重型托盘组成)如表 2所示.根据历史数据获得平均每天每托盘入库时间超过半小时,每托盘每小时将造成1元损失.两类叉车每天工作时长不超过10 h.
| 表 1 所选用叉车的参数 Table 1 Parameters of the chosen forklift |
| 表 2 各月份平均每日任务参数 Table 2 Average task parameters per day of each month |
在CPU主频为2.5 GHz的PC机上,在软件Matlab R2010b中使用遗传算法进行计算.以优化目标为目标函数,以目标函数的倒数为适应度函数,染色体采用二进制编码,种群规模大小取80,最大迭代次数取500,交叉概率取0.8,变异概率取0.05,对于不满足约束的染色体,将其适应度缩小1 000倍,减小其遗传的可能.将参数代入上节介绍的数学模型,经过40次上述遗传算法计算,获得最优配置结果为5辆内燃叉车、7辆电动叉车.
表 3列出了与最优配置方案接近的其他配置方案的年运营成本及最优内燃叉车任务数.比较方案1~4,可以看出随着电动叉车数量增多,方案2的年运营成本最低; 比较方案2、5~7,可以看出随着内燃叉车数的增多,方案2的年运营成本最低; 比较方案2、8~10,可以看出同时改变两类叉车数量,方案2的年运营成本最低.基本可以确定方案2是叉车配置的最优方案.同时,也可以观察到除在3、6、9、12这些繁忙月份,其余月份最优年运营成本均在内燃叉车任务数取任务下限值时,取得最优,因此在叉车的日常使用中,应当尽可能多地使用电动叉车.
| 表 3 优化配置结果对比1) Table 3 The comparison of optimal configuration results |
本文通过对采用按单生产模式企业的生产物流局部环节-成品入库过程进行分析,在考虑物流需求全年具有动态性和不确定性、运输资源具有可替换性、工作时间的约束下,基于排队论建立了以物流系统运作总成本为优化目标的运输资源的优化配置模型.并结合案例,应用遗传算法对模型进行求解,验证了该方法对于此类问题的有效性.为解决在生产物流运输需求具有动态性和不确定性、运输资源具有可替换性、工作时间约束条件下的物流运输资源配置问题,提出了一种有效的优化配置方法.本文对物流运输资源配置问题仅考虑了自有资源的配置,而未考虑公共租赁资源配置,另外对于叉车服务时间不服从负指数分布的情况,也没有进行深入研究.在今后的研究中可考虑在上述情况下该问题的配置方法该如何改进.
| [1] | 王悦. 企业物流管理[M]. 北京: 中国人民大学出版社, 2011. |
| [2] | 高朋涛. 基于计算机仿真技术的企业生产物流系统优化[D]. 上海海事大学物流工程学院, 2006. |
| [3] |
罗彦, 何利力. 带移库的多仓库烟草物流调度研究[J].
工业控制计算机, 2014, 27(1): 105-107.
Luo Y, He L L. Research on logistics scheduling library with moving more tobacco warehouse[J]. Industrial Control Computer, 2014, 27(1): 105-107. |
| [4] |
郭佩珍, 胡刚, 傅惠. 基于随机时间的车辆导航路径规划研究[J].
广东工业大学学报, 2012, 29(1): 35-38, 49.
Guo P Z, Hu G, Fu H. Research on path planning with random time for vehicle navigation[J]. Journal of Guangdong University of Technology, 2012, 29(1): 35-38, 49. |
| [5] |
汤雅连, 蔡延光, 郭帅, 等. 单车场关联物流运输调度问题的混沌遗传算法[J].
广东工业大学学报, 2013, 30(3): 53-57, 64.
Tang Y L, Cai Y G, Guo S, et al. Single-depot incident vehicle routing problem based on chaos genetic algorithm[J]. Journal of Guangdong University of Technology, 2013, 30(3): 53-57, 64. |
| [6] |
杨秋侠. 企业生产物流中物料搬运方式的优化[J].
物流技术, 2005, 24(6): 78-79, 90.
Yang Q X. Optimization of materials handling way in production logistics[J]. Logistics Technology, 2005, 24(6): 78-79, 90. |
| [7] |
宋伯慧, 王耀球. 装卸搬运设备配置优化研究[J].
物流技术, 2006, 25(7): 145-147.
Song B H, Wang Y Q. Study on optimized disposition of material handling equipment[J]. Logistics Technology, 2006, 25(7): 145-147. |
| [8] |
卢晓红, 贾振元, 刘弟新. 基于排队论的吊车精益生产调度研究[J].
计算机工程与应用, 2007, 43(26): 223-226.
Lu X H, Jia Z Y, Liu D X. Research on scheduling problem in lean production for crane service system based on queue theory[J]. Computer Engineering and Applications, 2007, 43(26): 223-226. DOI: 10.3321/j.issn:1002-8331.2007.26.065. |
| [9] |
李娜, 江志斌, 郑力, 等. 芯片封装系统两环闭型排队网络模型性能解析[J].
上海交通大学学报, 2010, 44(7): 1014-1018.
Li N, Jiang Z B, Zheng L, et al. Performance analysis of a two-loop closed queue network model in semiconductor assembly system[J]. Journal of Shanghai Jiaotong University, 2010, 44(7): 1014-1018. |
| [10] |
刘代平, 徐菱. 钢铁物流园区装卸搬运设备优化配置研究[J].
物流技术, 2013, 32(12): 237-240.
Liu D P, Xu L. Study on optimal deployment of loading and handling equipment in steel product logistics parks[J]. Logistics Technology, 2013, 32(12): 237-240. DOI: 10.3969/j.issn.1005-152X.2013.12.077. |
| [11] | 宋远卓. 物流配送中心搬运设备配置研究[D]. 西南交通大学机械工程学院, 2008. |
| [12] | Aleksandar Janjic. Two-step algorithm for the optimization of vehicle fleet in electricity distribution company[J]. Electrical Power and Energy Systems, 2015, 65(2): 307-315. |
| [13] |
赵援, 丁文英, 董绍华, 等. 基于排队论的天车合理数量的确定[J].
物流技术, 2008, 27(8): 217-219.
Zhao Y, Ding W Y, Dong S H, et al. How to determine the proper quantity of traveling crane based on queuing theory[J]. Logistics Technology, 2008, 27(8): 217-219. |
| [14] |
陈建宏, 郑海力, 刘浪. 基于排队论与灰色关联的露天矿排土车辆配置优化[J].
矿业研究与开发, 2009, 29(6): 3-5, 21.
Chen J H, Zheng H L, Liu L. Optimization of allocation of vehicles for waste disposal in open pit mine based on queuing and grey correlation theories[J]. Mining Research and Development, 2009, 29(6): 3-5, 21. |
| [15] |
张于贤, 于明, 叶冰冰. 基于开排队网络理论的生产线设备资源优化配置[J].
系统科学学报, 2012, 20(3): 75-78.
Zhang Y X, Yu M, Ye B B. Optimum distribution of equipment resources in production line based on open queuing network[J]. Journal of Systems Science, 2012, 20(3): 75-78. |
| [16] | 唐应辉, 唐小我. 排队论—基础与分析技术[M]. 北京: 科学出版社, 2006. |
| [17] | 邬万江. 物流中心机械设备数量配置方法研究[D]. 长春: 吉林大学交通学院, 2006. |
 2015, Vol. 32
2015, Vol. 32