全球定位系统(GPS)在制导、导航、精密测量、精密授时方面得到了广泛的应用,但由于GPS信号接收功率很低,在大多数情况下,GPS接收机工作在信噪比很低的环境中.而且,在现代复杂的电磁环境下,GPS接收机经常会受到各种有意、无意的干扰,干扰信号通常比GPS信号强很多,信噪比一旦低于-34dB[1],就很难有效捕获、跟踪到卫星信号,从而导致接收机无法正常定位,因此如何有效抑制干扰,提高接收机的抗干扰能力至关重要[2-4].
目前在GPS抗强干扰研究方面,通常是采用功率倒置算法[5-10],该算法对抑制强干扰信号效果显著,且干扰信号越强零陷越深,但同时也会对GPS信号产生抑制作用.此外,利用GPS接收机的合成天线阵列,可以通过补偿各个天线阵元接收信号的相位差来抑制多径干扰信号[11-15],但需要知道GPS信号的方向角.针对干扰信号很强,接收信号信噪比低于-34dB的情况,本文通过综合以上两种方法,利用功率倒置算法解调出GPS卫星信号,获取卫星星历参数,并利用加载于接收机上的惯性导航系统提供的接收机的坐标,计算GPS卫星相对于接收机的方向角,并通过对其进行相位补偿处理来增强信噪比,提高GPS接收机的抗干扰能力.
1 阵列天线接收信号模型假设有一GPS接收机,其接收天线阵列阵元数为M,阵元间距为d=0.5 λ ( λ 为GPS信号波长),信号入射方向与阵列法线的夹角定义为入射角度θ,如图 1所示,θ0为GPS信号的方向角,θ1为干扰信号的方向角.GPS信号源和P个干扰信号源同时发射信号,信号到达GPS接收机的方向角分别为θ0和θk(k=1, 2, 3, …, p),在t时刻,阵列接收的数据可表示为[16]
| $ \mathit{\boldsymbol{X}}\left( t \right) = \mathit{\boldsymbol{AS}}\left( t \right) + \mathit{\boldsymbol{n}}\left( t \right), $ | (1) |
| $ \mathit{\boldsymbol{y}} = \left[ {{x_0}\left( t \right),{x_1}\left( t \right), \cdots ,{x_{M - 1}}\left( t \right)} \right] \cdot \mathit{\boldsymbol{\omega }}, $ | (2) |
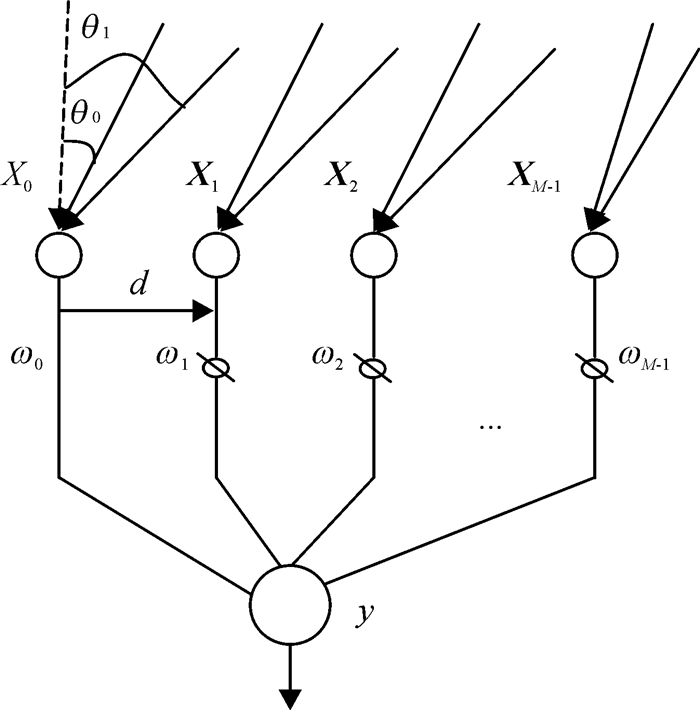
|
图 1 阵列天线接收信号模型 Figure 1 Array antenna signal receiving model |
式中X (t)为M×1阵列数据向量,
由于强干扰的影响,接收机接收到的GPS信号总是很微弱,为了提高接收机的抗干扰能力,本文先利用功率倒置算法对GPS信号进行预处理,因为在干扰信号很强的情况下,该算法能有效地增强GPS信号的信噪比,解调出GPS卫星信号的星历参数,获得卫星的坐标位置,但对于接收机定位所需的伪距等信息还不能正确解算出来.因此,本文通过在接收机上加载惯性导航系统做辅助,提供接收机的粗略位置,并结合卫星的坐标,计算出GPS信号相对接收机的大致方向角,然后通过天线阵列对GPS信号进行相位补偿处理,进一步增强GPS信号的信噪比,提高接收机的抗干扰能力,保证接收机的精确定位.图 2为本文抗干扰处理实现框图.
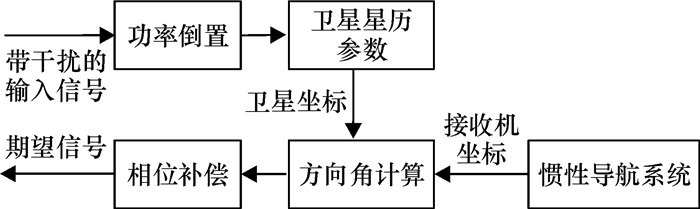
|
图 2 抗干扰处理实现框图 Figure 2 Anti-interference processing diagram |
一般情况下,干扰信号总是比GPS信号强很多,接收机接收到的卫星信号就比较微弱,甚至微弱到难以解调出卫星信号.针对干扰信号很强,接收信号信噪比低于-34dB的情况,本文通过功率倒置算法对其进行预处理, 以达到正确解调出GPS卫星星历参数的目的.
以阵元0上接收到的信号x0为参考信号,通过调整其他阵元的加权向量,从而使得阵列输出功率最小.令阵元0上的加权系数ω0=1,x =[x1, x2, x3, …, xM-1]T,可计算得到阵元1~M-1权值的最优解为
| $ {\mathit{\boldsymbol{\omega }}_{{\rm{opt}}}} = \mathit{\boldsymbol{R}}_{xx}^{ - 1} \cdot {\mathit{\boldsymbol{r}}_{x0}}. $ | (3) |
其中
| $ {\mathit{\boldsymbol{R}}_{xx}} = \mathit{\boldsymbol{E}}\left\{ {\mathit{\boldsymbol{x}} \cdot {\mathit{\boldsymbol{x}}^{\rm{T}}}} \right\},{\mathit{\boldsymbol{r}}_{x0}} = \mathit{\boldsymbol{E}}\left\{ {\mathit{\boldsymbol{x}} \cdot \mathit{\boldsymbol{x}}_0^{\rm{T}}} \right\}. $ | (4) |
该算法对输入端的信号(信号和干扰)均加以抑制,天线阵的方向图在强干扰和GPS信号方向上将形成零陷,零陷的深度与信号强度有关,且干扰越强零陷越深.如输入的信号很弱而干扰很强,干扰方向会产生很深的零陷从而被抑制,这相当于提高了信噪比.该算法的优点是不需要提前知道信号的结构以及接收信号的方向角,就可以在强干扰下获取GPS信号,从而解调出卫星星历参数.
2.2 方向角解算如图 3所示,对接收到的GPS信号获取其卫星星历参数,可得到卫星在WGS-84中的坐标(xs, ys, zs),利用加载于接收机U上的惯性导航系统提供的接收机的粗略位置( λu, φu)[17], 其在WGS-84中的坐标为(xu, yu, zu).
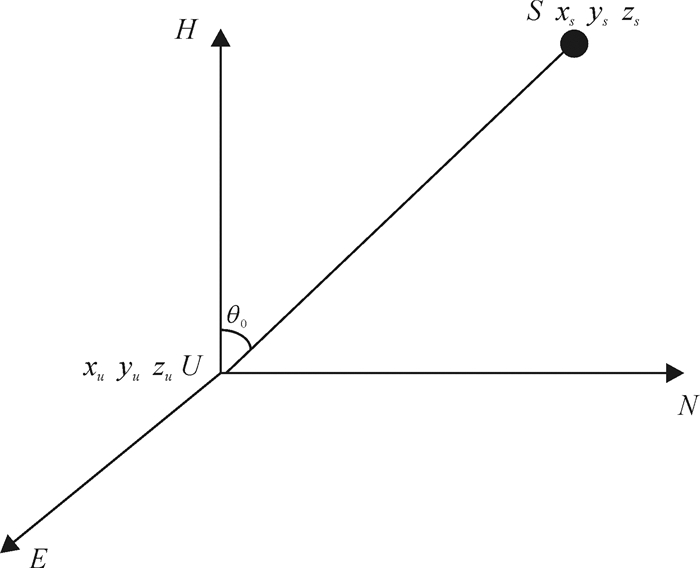
|
图 3 卫星相对接收机的方向角 Figure 3 Direction angle of satellite receiver |
GPS卫星与接收机之间的位置差为
| $ \Delta {x_{su}} = {x_s} - {x_u}, $ |
| $ \Delta {y_{su}} = {y_s} - {y_u}, $ |
| $ \Delta {z_{su}} = {z_s} - {z_u}. $ |
为计算卫星相对于接收机的方向,需要将WGS-84中GPS的坐标转换到观测点所在的站心坐标系中,其变换关系为
| $ \left[ {\begin{array}{*{20}{c}} {{\Delta _e}}\\ {{\Delta _n}}\\ {{\Delta _h}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \sin \lambda }&{\cos \lambda }&0\\ { - \sin \varphi cos\lambda }&{ - \sin \varphi \sin \lambda }&{\cos \varphi }\\ {\cos \varphi \cos \lambda }&{\cos \varphi \sin \lambda }&{\sin \varphi } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta {x_{su}}}\\ {\Delta {y_{su}}}\\ {\Delta {z_{su}}} \end{array}} \right], $ |
其中Δe为东向距离,Δn为北向距离,Δh为高度差.
从而可得到接收机在任意位置时GPS卫星相对于接收机的大致方向角为
| $ {\theta _0} = \arccos \left( {\left| {\frac{{\Delta h}}{{\sqrt {{{\left( {{\Delta _e}} \right)}^2} + {{\left( {{\Delta _n}} \right)}^2} + {{\left( {{\Delta _h}} \right)}^2}} }}} \right|} \right). $ | (5) |
针对计算得到的卫星信号的大致方向角,用天线阵列对GPS信号进行相位补偿处理如图 4所示.
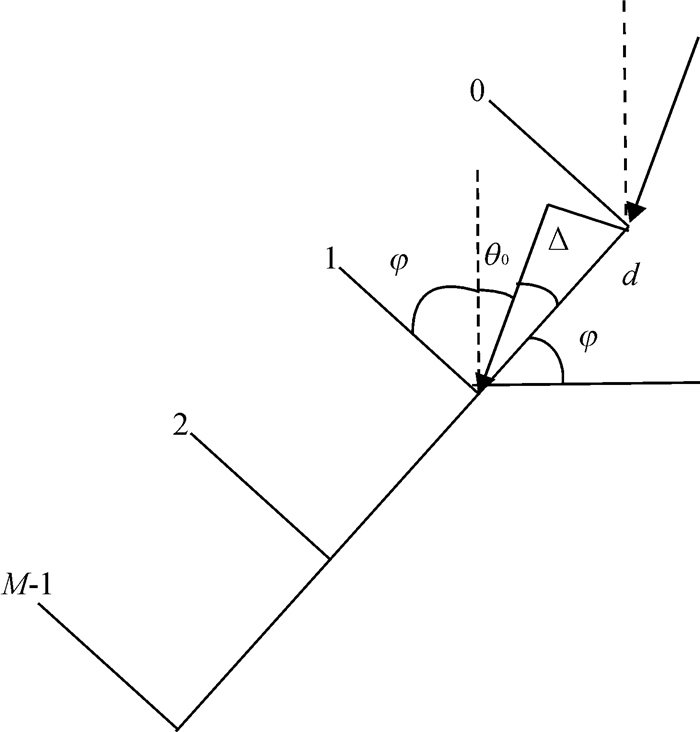
|
图 4 天线阵列补偿角度差 Figure 4 Antenna array compensation angle of difference |
设接收机的俯仰角为φ,则卫星信号与阵列天线的夹角为φ+θ0,可得阵元1到参考阵元0的波程差为
| $ \Delta = d\cos \left( {\frac{{\rm{ \mathsf{ π} }}}{2} - {\theta _0} - \varphi } \right). $ | (6) |
同理,各阵元到参考阵元的波程差为
| $ \begin{array}{l} {\Delta _m} = md\cos \left( {\frac{{\rm{ \mathsf{ π} }}}{2} - {\theta _0} - \varphi } \right),\\ m = 0,1,2, \cdots ,M - 1. \end{array} $ | (7) |
只补偿从GPS信号方向来的相位差,阵列输出为
| $ y = \sum\limits_0^{M - 1} {X\left( t \right)} \cdot \exp \left( {{\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}md}}{\lambda }\cos \left( {\frac{{\rm{ \mathsf{ π} }}}{2} - {\theta _0} - \varphi } \right)} \right). $ | (8) |
只对GPS信号方向进行相位补偿,并对各阵列输出求和,以此来增强信噪比,同时抑制干扰信号.
3 仿真结果对一在空中运行的飞行器,其天线阵列M为8, 阵元间距d为0.5 λ,采样数为2 000,信噪比SNR=-60 dB.通过功率倒置算法处理后,由卫星星历提供的卫星坐标及惯性量测装置提供的接收机坐标,利用公式(5)计算得到飞行器在某一位置时GPS卫星(PRN-5)相对于接收机的方向角θ0为36.5°.
在飞行器曲线运行过程中,飞行器运动过程的倾斜角φ分别为
|
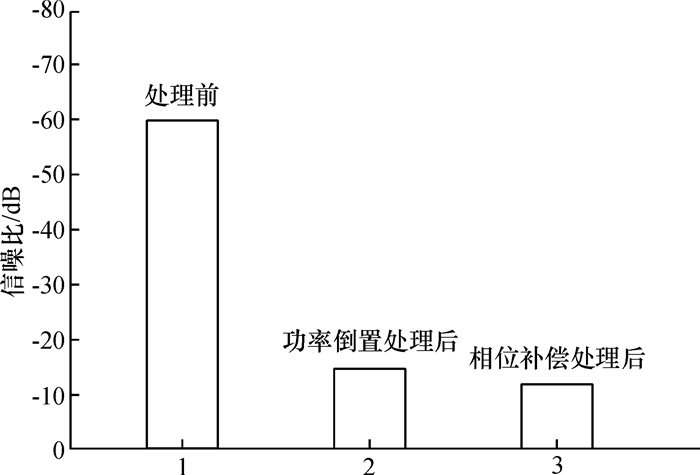
图 5 一个干扰源下处理前后信噪比对比图 Figure 5 SNR comparison before and after processing of one interference source |
|
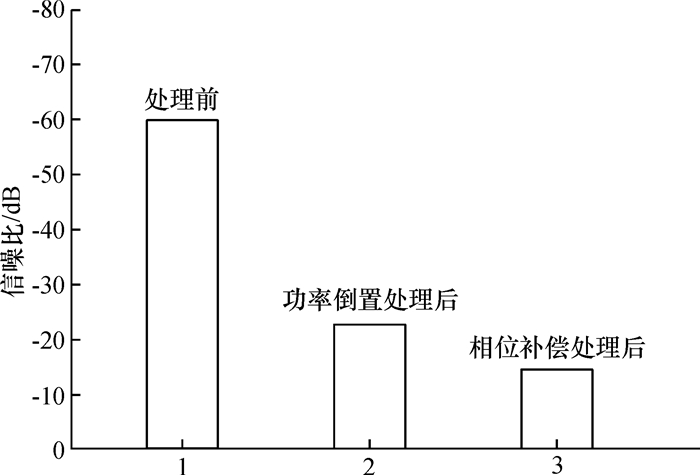
图 6 3个干扰源下处理前后信噪比对比图 Figure 6 SNR comparison before and after processing of three interference sources |
由图 5和图 6可看出,相位补偿处理比功率倒置算法处理能得到更高的信噪比,且在多个干扰源存在的情况下,经过功率倒置算法处理后,GPS信号的信噪比为-22.82dB,比功率倒置处理前提高了40.18dB,而相位补偿处理后,GPS信号的信噪比为-14.43dB,其信噪比再提升8.39dB,抗强干扰效果显著.另外,在1个和3个干扰源情况下,随输入信号的信噪比的改变,经过抗干扰处理后接收机接收信号的误码率如图 7和图 8所示.
|
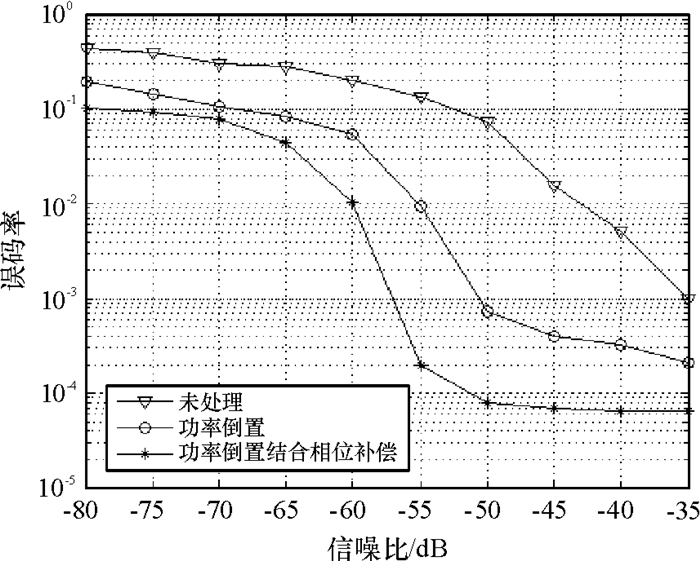
图 7 1个干扰源下误码率变化图 Figure 7 Error rate variation of one interference source |
|
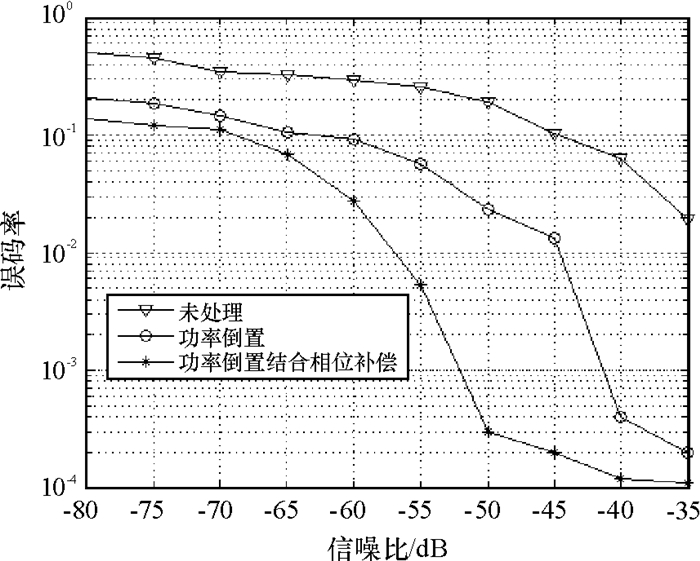
图 8 3个干扰源下误码率变化图 Figure 8 Error rate variation of three interference sources |
由图 7和图 8可看出,结合功率倒置算法与相位补偿的方法对信号处理后,接收机的误码率明显低于对信号不做处理和用功率倒置算法处理的误码率.图 8中,当信噪比高于-50dB时,接收机的误码率低于10-3,而对信号进行功率倒置算法处理时,当信噪比高于-40dB,接收机的误码率才能达到低于10-3,而对接收信号不做处理时,接收机的误码率始终高于10-2,可见在多个干扰源存在的情况下,结合功率倒置算法与相位补偿的方法也能保持较低的误码率.因此,结合功率倒置算法与相位补偿的方法能有效降低接收信号的误码率,提高接收机的抗干扰性能.
4 结束语本文对在强干扰环境下GPS信号的抗干扰处理进行研究,通过结合功率倒置算法和相位补偿的方法,达到增强GPS信号信噪比,抑制强干扰的效果.仿真结果表明该方法对增强GPS信号信噪比和抑制强干扰效果显著.
| [1] |
王婷婷, 王圣东, 陈欣. GPS干扰与抗干扰技术发展现状分析[J].
指挥控制与仿真, 2008, 30(6): 118-120.
Wang T T, Wang S D, Chen X. A survey on development of GPS jaming and anti-jamming technology[J]. Command Control & Simulation, 2008, 30(6): 118-120. |
| [2] |
向培胜. GPS抗干扰技术综述[J].
电讯技术, 2009, 49(10): 93-96.
Xiang P S. Summary of anti-jam technology for GPS[J]. Telecommunication Engineering, 2009, 49(10): 93-96. DOI: 10.3969/j.issn.1001-893x.2009.10.021. |
| [3] |
李瑞, 郭晓栋, 吴多龙. 一种层叠结构双频圆极化GPS天线的设计[J].
广东工业大学学报, 2011, 28(1): 28-31.
Li R, Guo X D, Wu D L. The design of dual-band stacked microstrip patch antennas for GPS applications[J]. Journal of Guangdong University of Technology, 2011, 28(1): 28-31. |
| [4] |
汪雪刚, 李瑞, 吴多龙. GPS双频圆极化微带天线的设计[J].
广东工业大学学报, 2011, 28(2): 43-46.
Wang X G, Li R, Wu D L. The design of dual-band circularly polarized patch antennas for GPS[J]. Journal of Guangdong University of Technology, 2011, 28(2): 43-46. |
| [5] |
赵晓东, 马煦, 瞿稳科. 功率倒置算法在GPS接收机天线抗干扰中的应用[J].
电讯技术, 2009, 49(7): 45-48.
Zhao X D, Ma X, Qu W K. Application of power inversion arithmetic in anti-interference design of GPS receiver antenna[J]. Telecommunication Engineering, 2009, 49(7): 45-48. |
| [6] |
何永前, 李建璜. GPS抗干扰接收机自适应天线阵功率倒置算法研究[J].
舰船电子工程, 2012, 32(6): 61-62, 79.
He Y Q, Li J H. GPS receiver adaptive anti-interference antenna array power inversion algorithm[J]. Ship Electronic Engineering, 2012, 32(6): 61-62, 79. |
| [7] |
周云锋, 李宏, 梁宏. GPS接收阵列自适应抗干扰算法性能比较[J].
计算机仿真, 2011, 28(1): 68-71, 91.
Zhou Y F, Li H, Liang H. Comparison between adaptive anti-jamming algorithms applying in GPS arrays[J]. The Computer Simulation, 2011, 28(1): 68-71, 91. |
| [8] |
张文明. GPS自适应天线阵多波束形成算法分析[J].
兵工学报, 2010, 31(12): 1686-1690.
Zhang W M. Analysis of multi-beamforming algorithms for GPS adaptive array[J]. Acta Armamentarii, 2010, 31(12): 1686-1690. |
| [9] | 王新怀. 卫星导航抗干扰接收系统技术研究[D]. 西安: 西安电子科技大学网络与继续教育学院, 2010. |
| [10] | 王纯. 卫星导航接收机自适应抗干扰方法研究[D]. 西安: 西安电子科技大学网络与继续教育学院, 2011. |
| [11] | Wang L, Feng S A, Yang R Y. Synthetic array processing for GNSS receiver in multipath environments[J]. Automatic Control and Artificintelligence, 2012: 2026-2029. |
| [12] | Draganov S, Harlacher M, Haas L. Synthetic aperture navigation in multipath environments[J]. Wireless Communications, 2011, 18(2): 52-58. DOI: 10.1109/MWC.2011.5751296. |
| [13] | Leong W, Patel K, Weinfield J. Synthetic aperture navigation algorithms applied to a driving user inmultipath environments[C]//Position Location and Navigation Symposium. Myrtle Beach, SC : IEEE, 2012: 673-677. |
| [14] | Prater J L, Marston T M. Partial synthetic aperture beamformer[C]//OCEANS 2011. Waikoloa, HI: IEEE, 2011: 1-5. |
| [15] | Ahmad Z, Tahir M, Ali I. Analysis of beamforming algorithms for antijams[C]//Direct and Inverse Problems of Electromagnetic and Acoustic Wave Theory. Lviv : IEEE, 2013: 89-96. |
| [16] | 狄旻珉. GPS抗干扰接收技术研究[D]. 长沙: 国防科学技术大学电子科学与工程学院, 2006. |
| [17] |
史文森, 朱海, 蔡鹏. 基于接收信号DOA估计的GPS欺骗式干扰信号识别技术[J].
舰船科学技术, 2013, 35(4): 111-116.
Shi W S, Zhu H, Cai P. The SPS deception jamming identification technology of based on the DOA of received signal[J]. Ship Science and Technology, 2013, 35(4): 111-116. |
 2015, Vol. 32
2015, Vol. 32