2. 广东工业大学 经济与贸易学院,广东 广州 510520
2. School of Economics and Commerce, Guangdong University of Technology, Guangzhou 510520, China
改革开放以来,我国经济社会发展取得了举世瞩目的成就,尤其是广东地区,经济持续快速增长,许多领域走在全国前列,发挥了排头兵作用.2010年广东实现GDP 45 636亿元人民币,人均46 990元,GDP 30年年均增长13%以上;2011年,广东GDP达52 673亿元人民币,成为国内首个迈入5万亿大关的省份;2012年,广东GDP达到51 477亿元人民币,仍位居全国榜首.尽管2013的经济数据尚未全面发布,专家预计2013年全省生产总值6.23万亿元,突破1万亿美元,比上年增长8.5%.经济发展的同时,劳资矛盾也日益凸显,近年来珠三角地区劳资纠纷呈现出两大趋势:一是劳资纠纷的数量明显扩大,二是群体性事件增多.尤其是2008~2009年金融危机期间,仅广州市就有497家企业欠薪逃逸,涉及到员工两万多人,个别企业发生集体上访的事件.2008年,在广州市各类不稳定因素里面,由于劳资纠纷引发的事件所占比重达38%,在各类因素中是第一位的.“广本”事件、“富士康”事件,实质上就是劳资紧张关系未能得到适当消解的集中表现.据广州市人力资源和社会保障局公布的数据:2013年上半年,仅广州市发生30人以上的劳资纠纷群体性事件达126宗;各级劳动人士争议仲裁机构受理案件13 519宗,涉及劳动者人数20 605人.劳资冲突已成为制约当地经济健康、有序发展的阻碍.毫无疑问,劳资关系和谐与否,不仅关系到经济社会转型能否顺利进行,而且关系到我们能否继续维持和谐稳定的改革开放大局.
1 文献综述关于劳资关系问题,国内外很多学者都进行了研究.就我国来说,国内学术界几乎一致认为我国当前的劳资关系存在“资强劳弱”的格局,很多学者主张借鉴西方的调节机制,同时结合本国国情,针对劳资矛盾,从劳方、资方、政府、社会等角度提出相应的解决措施.任小平等[1]认为制度救济为工会的博弈劣势提供了基础,也为工会在劳资博弈中主动作为提供了可能.罗宁[2]在其学位论文中探讨了现代劳资关系演变中产生的两级扩展:劳方、资方、管理者三方为第一级;劳方、资方、政府三方为第二级,并结合转型期中国劳资关系运行的具体实践,提出当前协调劳资关系、控制社会风险、构建和谐社会的现实选择和政策建议.温春继[3]认为我国劳资关系紧张的主要原因之一是资方变态地追求利润,忽视劳动者的权益以及有法不依,执法不严,并提出要从健全法律法规、发挥工会作用等缓解劳资矛盾的措施.李玉燕[4]分析了私营企业劳资博弈的囚徒困境,提出政府在促进劳资合作中应有所作为、发挥企业在促进劳资合作中的作用、劳动者要努力增强在劳资博弈中的力量等对策和建议.刘金祥[5]提出在我国强资本弱劳工的情形下,需要以政府调节劳资关系模式为主导,充分发挥工会作用,构建机体谈判制度等多元化手段来调整劳资关系.王明亮[6]认为强化企业“自制型”工会组织的建设,增强劳工博弈能力确保企业对于人力资本投资的“准租”分成,激发企业积极性是优化劳资关系的有效措施之一.美国密歇根大学的教授Gallagher M E[7]探讨了过去近20年里,在经济转型的环境下中国劳资关系的改变.从研究方法看,很多相关文献主要采取了比较研究、案例分析、问卷调查等多种方法,但计量、建模等方法运用相对较少.运用演化博弈理论,将劳资双方的利益得失进行量化,有利于分析劳资双方策略选择的动态调整过程.
演化博弈理论目前在经济学领域比较流行,黄凯南[8]探讨了演化博弈与演化经济学的互补性,王文宾[9]指出国内外演化博弈论的研究进展.在现实生活中,经典博弈论要求的参与人完全理性的条件很难达到,参与人的选择常常具有非理性的特征.此特征的存在源于参与人之间的认知能力的差异、信息沟通及传递的限制,使博弈参与人的决策不是完全理性的,而是具有有限理性,即介于完全理性和非完全理性之间的一定限制下的理性.有限理性意味着博弈双方不可能通过一次博弈就找到理想的均衡策略,需要通过“试错”的重复博弈来调整策略选择.
演化博弈基于有限理性,以人群为研究对象,分析动态演化过程,选择和突变是其两个基本方面.选择指能够获得较高支付的策略在以后将被更多的参与者采用,突变是指部分个体以随机的方式选择不同群体的策略[10].本文运用演化博弈理论方法探讨劳资关系问题, 博弈的参与人具有限理性,博弈双方群体在不断试错的过程中,调整和改进策略选择,最终达到利益均衡、关系和谐的稳定状态.这样就找到了劳资关系协调与演化博弈的契合之处.运用演化博弈论进行劳资利益协调机制的研究,有助于学界深化对于相关问题的认识,充实、完善劳资关系理论.
纵观我国劳资关系的变化发展,劳资双方的地位一直都是不对等的,从利益不均衡、关系稳定,到利益不均衡、关系不稳定,双方一直在磨合演变,但尚未达到利益均衡、关系稳定的和谐状态.劳资利益协调机制的核心只能是劳资双方直接参与的利益互动博弈机制,政府和工会只是当前劳资利益失衡时,强化劳工博弈能力的辅助力量,而不是利益需要平衡的主体本身.由于劳资双方及政府的策略是通过很长一段时间的模仿、学习来调整的,本文将从演化博弈的角度出发,建立劳资双方博弈模型以及资方与政府间的博弈模型,找出双方的稳定点.根据分析结果提出改进劳资关系的措施,促进劳资双方和谐相处,稳定发展.
2 劳资双方博弈模型假设与求解分析 2.1 模型假设以劳动力市场上的劳方(L)和资方(C)分别为两个群体,作为博弈的两方参与人.在确定成为雇佣关系的情况下,双方都有两种策略可选:合作(S1)和不合作(S2),合作可以理解为履行合约,不合作可以理解为违约.劳方选择合作的概率为x,不合作的概率为1-x,资方选择合作的概率为y,选择不合作的概率为1-y,概率也可以理解为群体博弈中选取该策略的参与人比例.双方的策略及收益如表 1矩阵所示.
| 表 1 博弈支付矩阵 Table 1 Payoff matrix of the game |
其中,劳资双方有任一方选择“合作”策略理解为双方达成协议,产生雇佣关系,双方都选择“不合作”意味着双方不存在雇佣关系.(合作,合作)表示劳方卖力工作,完成了规定的全部劳动,资方也支付了协议的所有报酬;(合作,不合作)表示劳方认真完成了劳动但是资方没有付给报酬,如拖欠工资等;(不合作,合作)表示劳方在工作中没有尽力,但是资方仍然支付了全部报酬.π1、π2分别为劳方和资方正常情况下(无雇佣关系)时各自的收益[11],Δπ为双方合作(产生雇佣关系)产生的总利润,α1、α2分别为双方利润分配系数,α1+α2≤1,c为总的生产成本,β1、β2分别为双方分摊成本系数,β1+β2≤1,β1c表示劳方付出的劳动等,β2c表示资方支付薪酬、生产资料等的消耗,ε1、ε2分别表示劳资双方的背叛收益,一方因辜负对方的付出而得到的收益.例如劳方付出了劳动,但是资方没有支付相应的报酬,ε2为资方因背叛劳方得到的收益.
2.2 模型求解与分析劳方两种情况的期望收益EL(Si),i=1,2和总的期望收益E(L)分别为
| $ {E_L}\left( {{S_1}} \right) = y\left( {{\pi _1} + {\alpha _1}\Delta \pi - {\beta _1}c} \right) + \left( {1 - y} \right)\left( {{\pi _1} - {\beta _1}c} \right), $ |
| $ {E_L}\left( {{S_2}} \right) = y\left( {{\pi _1} + {\varepsilon _1}} \right) + \left( {1 - y} \right){\pi _1}, $ |
| $ E\left( L \right) = x{E_L}\left( {{S_1}} \right) + \left( {1 - x} \right){E_L}\left( {{S_2}} \right). $ |
资方两种情况的期望收益EC(Si),i=1,2和总的期望收益E(C)分别为
| $ {E_C}\left( {{S_1}} \right) = x\left( {{\pi _2} + {\alpha _2}\Delta \pi - {\beta _2}c} \right) + \left( {1 - x} \right)\left( {{\pi _2} - {\beta _2}c} \right), $ |
| $ {E_C}\left( {{S_2}} \right) = x\left( {{\pi _2} + {\varepsilon _2}} \right) + \left( {1 - x} \right){\pi _2}, $ |
| $ E\left( C \right) = y{E_C}\left( {{S_1}} \right) + \left( {1 - y} \right){E_C}\left( {{S_2}} \right). $ |
在不断地调整策略中,对于参与方来说,如果某一特定策略的平均收益高于混合策略的平均收益,那么其更倾向于使用这种特定策略.这里假设参与方使用此策略频率的相对调整速度与其收益超过平均收益的幅度成正比,则可以得到动态复制系统[12]:
| $ F\left( x \right) = \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = x\left( {1 - x} \right)\left[ {y\left( {{\alpha _1}\Delta \pi - {\varepsilon _1}} \right) - {\beta _1}c} \right], $ |
| $ F\left( y \right) = \frac{{{\rm{d}}y}}{{{\rm{d}}t}} = y\left( {1 - y} \right)\left[ {x\left( {{\alpha _2}\Delta \pi - {\varepsilon _2}} \right) - {\beta _2}c} \right]. $ |
根据微分方程理论,若存在(x, y)使得F(x)=0,F(y)=0,则(x, y)为平衡点,显然,该动态复制方程的平衡点为E1(0, 0),E2(1, 0),E3(0, 1),E4(1, 1);令
根据Friedman提出的方法,一个由微分方程系统描述的群体动态,其平衡点的稳定性是由该系统得到的雅克比(Jacobi)矩阵的局部稳定分析得到的,由动态复制系统得雅克比(Jacobi)矩阵为
| $ \left[ {\begin{array}{*{20}{c}} \begin{array}{l} \left( {1 - 2x} \right)\left[ {y\left( {{\alpha _1}\Delta \pi - {\varepsilon _1}} \right)} \right] - {\beta _1}c\\ y\left( {1 - y} \right)\left( {{\alpha _2}\Delta \pi - {\varepsilon _2}} \right) \end{array}&\begin{array}{l} x\left( {1 - x} \right)\left( {{\alpha _1}\Delta \pi - {\varepsilon _1}} \right)\\ \left( {1 - 2y} \right)\left[ {x\left( {{\alpha _2}\Delta \pi - {\varepsilon _2}} \right)} \right] - {\beta _2}c \end{array} \end{array}} \right]. $ |
下面,分析平衡点E1~E5的局部稳定性.α1Δπ-ε1>β1c,α2Δπ-ε2>β2c,由复制动态方程,雅克比(Jacobi)矩阵和李雅普诺夫第一方法可得平衡点的局部稳定性结果如表 2所示.
| 表 2 平衡点的局部稳定性分析结果 Table 2 Results of local asymptotic stability analysis of equilibrium points |
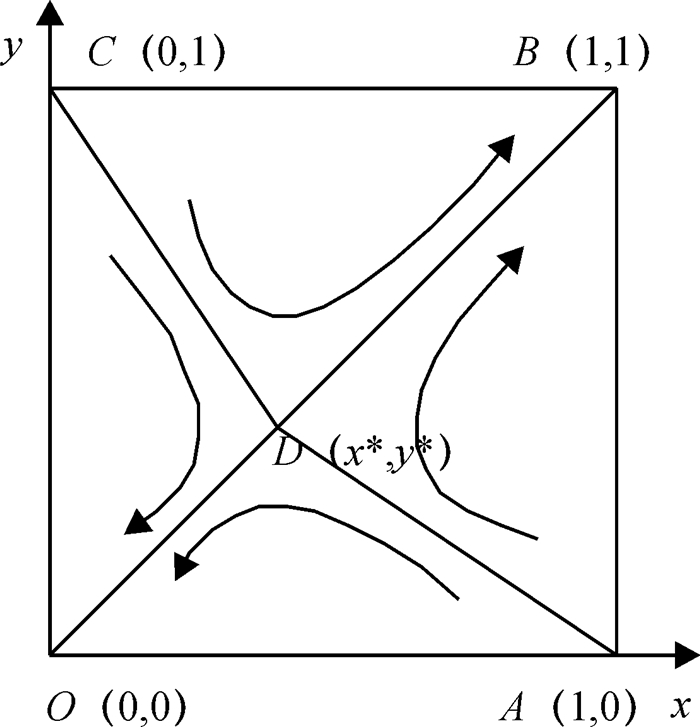
表 2中的ESS(Evolutionary Stable Strategy)表示演化稳定策略.由表 2可以看出,E1(0, 0)和E4(1, 1)是演化博弈的渐近稳定点,对应的策略是演化稳定策略.演化相位图如图 1所示.
|
图 1 劳资双方博弈演化相图 Figure 1 Game evolutionary phase spectrum of L & C |
图 1中,横轴x表示劳方选择合作的概率,纵轴y表示资方选择合作的概率,以下各图均同.由演化相图可得出与表 2相同的结论,在长期演化的过程中,系统会保持着一种合作与不合作共存的状态,演化的结果是双方要么都合作要么都不合作.图 1中以折线C-D-A为界,在折线的左下部分,系统收敛于双方不合作,即x=0,y=0时,劳资双方选择合作的概率均为0,即(不合作,不合作)为双方的演化稳定策略.对于劳方来说,分得的利润少,而分摊的成本高,辛勤的工作得不到应有的回报,选择不合作得到的收益高于合作时得到的收益.对于资方来说,支付给劳方的报酬高,自己的所得利润少,选择不合作,维持自己原有的利润收益更大.
图 1中,在折线C-D-A的右上部分,系统收敛于双方合作,当x=1,y=1时,劳资双方选择合作的概率为1,即(合作,合作)为演化稳定策略.对于劳方来说,他认真完成了工作并得到了相应的报酬,此时的收益大于不与资方合作时的收益.对于资方来说,选择“合作”意味着与劳方达成劳资协议并且按协议支付给劳方报酬,α2Δπ>β2c,合作时候的收益大于不合作时的收益.此时,劳资双方的收益均大于不合作时的收益,(合作,合作)是双方的最优选择,是演化稳定策略.
演化结果向哪个方向发展由SCBAD和SCOAD所决定,面积越大表明概率越大,现实生活中,希望双方能向(合作,合作)的方向发展,就要使得折线C-D-A的右上部分的图形面积比左下部分的图形面积大.设S1表示四边形COAD的面积,S2表示四边形CBAD的面积,分别为:
| $ {S_1} = \frac{1}{2}\left( {\frac{{{\beta _2}c}}{{{\alpha _2}\Delta \pi - {\varepsilon _2}}} + \frac{{{\beta _1}c}}{{{\alpha _1}\Delta \pi - {\varepsilon _1}}}} \right),{S_2} = 1 - {S_1}. $ |
可以看出,S1与生产成本c、劳资双方分担成本的比例βi、双方合作生产的利润Δπ、对利润的分配比率αi以及背叛收益εi相关.
α1与α2存在某种比例关系,现假设α2=α,α1=k-α,其中,k为常数且满足0 < k < 1,代入S1的表达式:
同样,β1与β2存在某种比例关系,现假设β2=β,β1=g-β,其中,g为常数且满足0 < g < 1.代入S1的表达式:
在我国“资强劳弱”的局面下,政府等监管部门应该站在劳动者的立场上,保障劳动者的利益不受资方的侵害.政府部门有缓和劳资矛盾、优化劳资关系的责任和职能要求,政府部门可能选择对企业进行认真监管,保障劳方利益不受损害; 也可能注重经济效益,对企业的违约行为视而不见,以求得当地经济水平的增长.在企业与政府部门的博弈中,企业守约的概率为x,违约的概率为1-x,假设政府部门只要认真监管就可以查出企业是否存在违约行为,政府认真监管的概率为y,不监管的概率为1-y,双方的策略及收益如表 3矩阵所示.
| 表 3 博弈支付矩阵 Table 3 Payoff matrix of the game |
此支付矩阵中,π1、π2分别为企业和政府正常情况下的收益,此时,企业守约经营,政府不监管.c2为政府监管所付出的成本.当政府实行认真监管,政府对守约的企业给予一定的物质或荣誉奖励,记为η,p为对企业违约的惩罚,c1为企业违约而造成的失信、形象损坏等损失,a为政府因监管有力,维护了劳方利益而得到的声誉等“潜性政绩”,ε为企业因违约而获得的额外收益,b为政府不监管引起的民怨等造成的损失,d表示企业因违约而增加收益使得政府获得经济增长的“显性政绩”.
3.2 模型求解与分析资方两种情况的期望收益EC(Si),i=1, 2和总的期望收益E(C)分别为
| $ {E_C}\left( {{S_1}} \right) = y\left( {{\pi _1} + \eta } \right) + \left( {1 - y} \right){\pi _1}, $ |
| $ {E_C}\left( {{S_2}} \right) = y\left( {{\pi _1} + \varepsilon - p - {c_1}} \right) + \left( {1 - y} \right)\left( {{\pi _1} + \varepsilon - {c_1}} \right), $ |
| $ E\left( C \right) = x{E_C}\left( {{S_1}} \right) + \left( {1 - x} \right){E_C}\left( {{S_2}} \right). $ |
政府两种情况的期望收益EG(Si),i=1,2和总的期望收益E(G)分别为
| $ {E_G}\left( {{S_1}} \right) = x\left( {{\pi _2} - {c_2}} \right) + \left( {1 - x} \right)\left( {{\pi _2} - {c_2} + a} \right), $ |
| $ {E_G}\left( {{S_2}} \right) = x{\pi _2} + \left( {1 - x} \right)\left( {{\pi _2} - b + d} \right), $ |
| $ E\left( G \right) = y{E_G}\left( {{S_1}} \right) + \left( {1 - y} \right){E_G}\left( {{S_2}} \right). $ |
同2.2的模型求解与分析可以得到此模型的动态复制系统和雅克比(Jacobi)矩阵.即动态复制系统为
| $ F\left( x \right) = \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = x\left( {1 - x} \right)\left[ {y\left( {\eta + p} \right) + \left( {{c_1} - \varepsilon } \right)} \right], $ |
| $ F\left( y \right) = \frac{{{\rm{d}}y}}{{{\rm{d}}t}} = y\left( {1 - y} \right)\left[ {x\left( {d - a - b} \right) + \left( {a + b - {c_2} - d} \right)} \right]. $ |
由此得雅克比(Jacobi)矩阵为
| $ \left[ {\begin{array}{*{20}{c}} \begin{array}{l} \left( {1 - 2x} \right)\left[ {y\left( {\eta + p} \right) + \left( {{c_2} - \varepsilon } \right)} \right]\\ y\left( {1 - y} \right)\left( {d - a - b} \right) \end{array}&\begin{array}{l} x\left( {1 - x} \right)\left( {\eta + p} \right)\\ \left( {1 - 2x} \right)\left[ {x\left( {d - a - b} \right) + \left( {a + b - {c_2} - d} \right)} \right] \end{array} \end{array}} \right]. $ |
由F(x)=0,F(y)=0,显然,该动态复制方程的平衡点为E1(0, 0),E2(1, 0),E3(0, 1),E4(1, 1);
本模型较复杂,故采用分情况论述的方法分析,由F(x)=0可得其解xi,若F′(x) < 0,则xi为演化稳定策略(ESS).
对于资方来说:(1) 0 < y < 1,当c1>ε时,有x1=0,x2=1为稳定状态,y(η+p)+(c1-ε)>0恒成立,F′(0)>0,F′(1) < 0,故x1=0不是演化稳定策略,x2=1为演化稳定策略.(2) c1 < ε,当
对于政府方面来说,(1) 0 < x < 1,当c2>a+b-d>0时,x(d-a-b)+(a+b-c2-d) < 0恒成立,F′(0) < 0,F′(1)>0,y1=0为演化稳定策略.(2) a+b-d < 0,当
下面用演化相图对不同条件下的资方与政府间的博弈作进一步分析(见图 2~5).
|
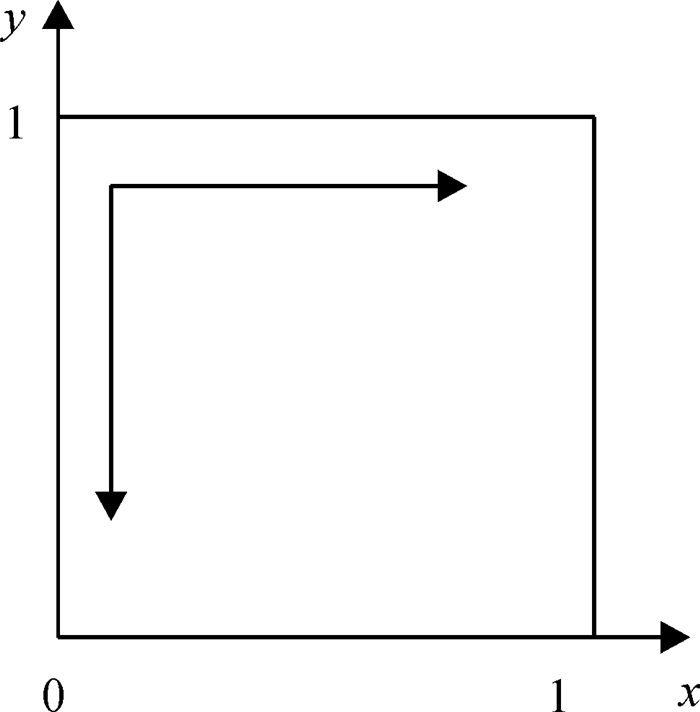
图 2 c1>ε,c2>a+b-d>0时,资方与政府博弈演化相图 Figure 2 Game evolutionary phase spectrum of C&G when c1>ε, c2>a+b-d>0 |
|
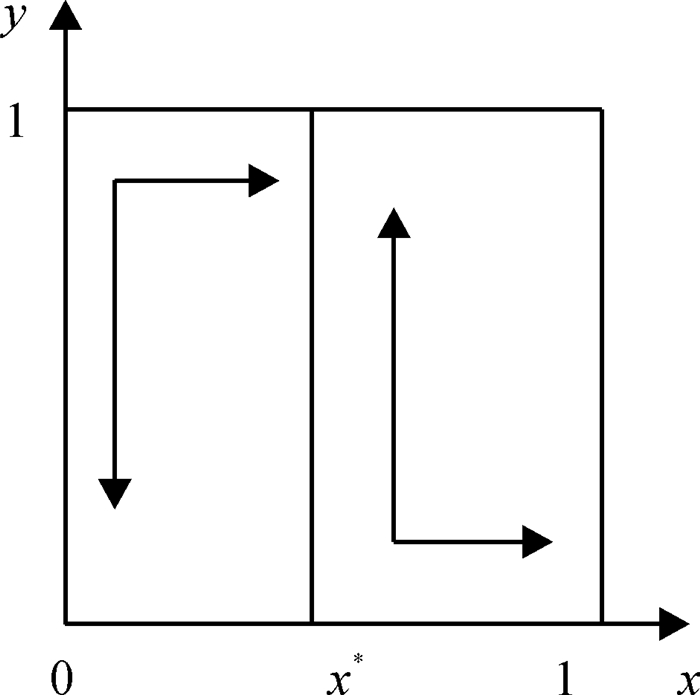
图 3 c1>ε,a+b-d < 0时,资方与政府博弈演化相图 Figure 3 Game evolutionary phase spectrum of C&G when c1>ε, a+b-d < 0 |
|
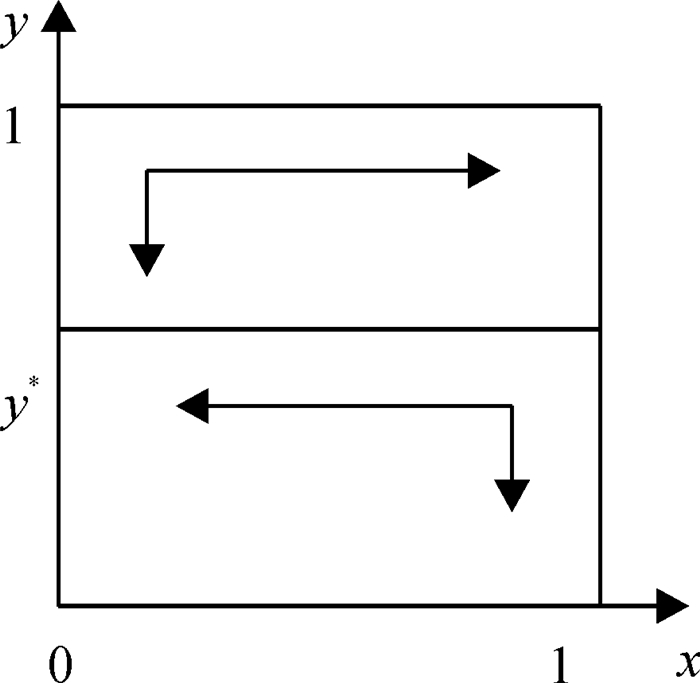
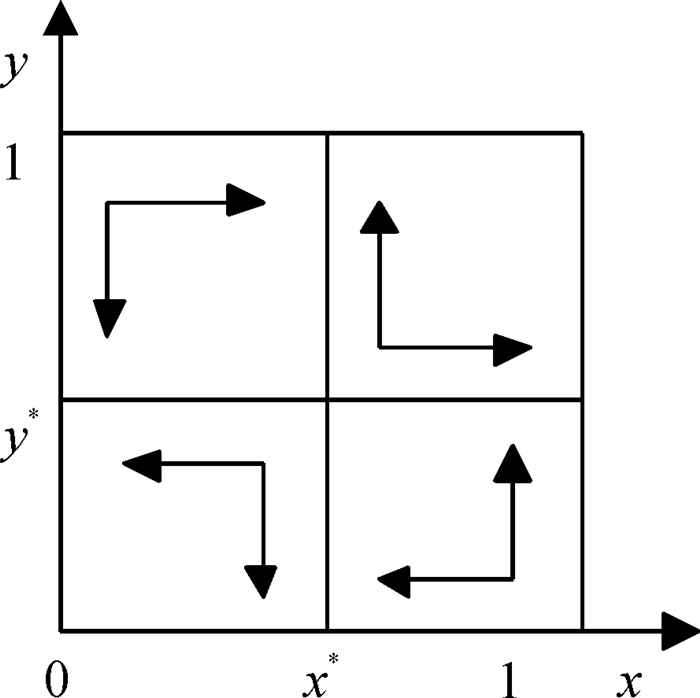
图 4 c1 < ε,c2>a+b-d>0,资方与政府博弈演化相图 Figure 4 Game evolutionary phase spectrum of C&G when c1 < ε, c2>a+b-d>0 |
|
图 5 c1 < ε,a+b-d < 0时,资方与政府博弈演化相图 Figure 5 Game evolutionary phase spectrum of C&G when c1 < ε, a+b-d < 0 |
图 2中,当c1>ε,c2>a+b-d>0,时,长期演化的结果为x=1,y=0,演化稳定策略为政府不监管,企业守约经营.企业违约的损失足够大,守约的收益大于违约的收益,政府部门也节约了监管成本.
图 3中,当c1>ε,a+b-d < 0时,长期演化的结果为x=1,y=1,演化稳定策略为政府认真监管,企业守约经营.在政府的有力监管下,企业若违约必有损失,因此选择守约以获取额外的奖励来扩大利益.
图 4中,当c1 < ε,c2>a+b-d>0时,长期演化的结果为x=0,y=0,演化稳定策略为政府不监管,企业违约.政府由于监管成本高等原因选择不监管,即使企业违约也不会有来自政府的惩罚,企业更倾向于选择违约以获取更大的利益.
图 5中,当c1 < ε,a+b-d < 0时,此时,政府和企业的策略选择不收敛于任何一点[15].当c1→ε时,y→0,即政府选择不监管,也就是说当c1足够大,企业违约的成本就大,显然,守约所获的利益大于违约时的利益,政府推测企业一定会选择守约,政府就没有监管的必要,也节约了成本.当c2→0时,x→1,企业选择守约.监管成本越低,政府选择监管的概率就越大.企业为避免因违约造成的形象损坏、惩罚等损失,会选择守约经营.
4 结论根据以上对于劳资双方博弈分析、资方(企业)与政府间的博弈分析可知,为了维护弱势方——劳方的利益,协调劳资双方不对等的地位,促使其走向稳定的、双赢的合作关系,优化市场的资源配置[16],政府等监管部门应该恪尽职守,政府的作用在于提供一个公平的市场经济环境,为雇主和员工搞好服务.监管机构应该给予守约经营的企业以奖励(η),同时加大检查力度及对企业违约的惩罚(p),不仅要使违约企业受到金钱上的惩罚,还要曝光其不法行为(c1),通过社会舆论压力给予其一定的约束;代表劳方的工会组织要积极参与谈判协商,平衡劳资双方的力量,为劳方争取较大的利润分配比例(α1);企业方面,要有社会责任感,要严守合约,提高自身信誉(y),还应重视科技创新和研发以提高生产效率,降低生产成本(c).对本文所关注的问题进行深入研究还可以构建基于演化博弈的三方博弈模型,综合考虑劳方、资方以及政府监管部门在劳资关系博弈中的策略及收益,建立三方协调机制,确保劳资关系稳定发展.
| [1] |
任小平, 许晓军. 劳资博弈:工资合约中的制度救济与工会行为[J].
学术研究, 2009(2): 81-87.
Ren X P, Xu X J. Labour game: the system of relief and union conduct in wage contracts[J]. Academic Research, 2009(2): 81-87. |
| [2] | 罗宁. 中国转型期劳资关系冲突与合作研究[D]. 成都: 西南财经大学经济学院, 2009. |
| [3] |
温春继. 目前我国劳资关系紧张的主要原因及对策[J].
中国劳动关系学院学报, 2010, 24(2): 77-80.
Wen C J. The causes and countermeasures of tense labor-management relations in China[J]. Journal of China Institute of Industrial Relations, 2010, 24(2): 77-80. |
| [4] |
李玉燕. 我国私营企业劳资博弈的囚徒困境及其求解[J].
西安财经学院学报, 2011, 24(3): 15-18.
Li Y Y. The private enterprise of labor game prisoner dilemma and solution in China[J]. Journal of Xi'an University of Finance and Economics, 2011, 24(3): 15-18. |
| [5] |
刘金祥. 多元化路径:我国劳资关系调整模式的反思和重构[J].
社会科学研究, 2011(1): 55-61.
Liu J X. Diversification path:reflection and reconstruction in the mode of labor relations adjustment[J]. Social Science Research, 2011(1): 55-61. |
| [6] |
王明亮. 技术进步与劳资关系优化研究[J].
商业研究, 2012, 425(9): 21-25.
Wang M L. Research on technological progress and optimization of labor relations[J]. Commercial Research, 2012, 425(9): 21-25. |
| [7] | Gallagher M E. "Time is money, efficiency is life": The transformation of labor relations in China[J]. Studies in Comparative International Development, 2004, 39(2): 11-44. DOI: 10.1007/BF02686276. |
| [8] |
黄凯南. 演化博弈与演化经济学[J].
经济研究, 2009(2): 132-145.
Huang K N. Evolutionary games and evolutionary economics[J]. Economic Research, 2009(2): 132-145. |
| [9] |
王文宾. 演化博弈论研究的现状与展望[J].
统计与决策, 2009(3): 158-161.
Wang W B. Status and prospects of research on evolutionary game theory[J]. Statistics & Decision, 2009(3): 158-161. |
| [10] | Weibull J W. Evolutionary game theory[M]. Cambridge, Massachusetts: The MIT Press, 1995. |
| [11] |
熊强. 供应链企业间安全信息共享的演化博弈分析[J].
科技管理研究, 2011, 15(15): 181-183.
Xiong Q. Evolutionary game analysis of information security sharing in supply chain[J]. Science and Technology Management Research, 2011, 15(15): 181-183. DOI: 10.3969/j.issn.1000-7695.2011.15.047. |
| [12] | Friedman D. Evolutionary games in economics[J]. Econometrica, 1991, 59(3): 637-666. DOI: 10.2307/2938222. |
| [13] |
黄敏镁. 基于演化博弈的供应链协同产品开发合作机制研究[J].
中国管理科学, 2010, 18(6): 155-162.
Huang M M. Evolutionary game analysis of cooperation mechanism for collaborative product development in supply chain[J]. Chinese Journal of Management Science, 2010, 18(6): 155-162. |
| [14] |
卫锋. 尊弈视角下供应链信息共享的利益协调机制研究[J].
物流技术, 2013, 32(4): 214-216.
Wei F. A game perspective on mechanism of benefit coordination in supply chain information sharing[J]. Logistics Technology, 2013, 32(4): 214-216. |
| [15] |
朱怀念, 张成科, 李云龙, 等. 一类不定仿线性二次型随机微分博弈的鞍点均衡策略[J].
广东工业大学学报, 2012, 29(3): 35-38.
Zhu H N, Zhang C K, Li Y L, et al. Saddle-point equilibrium strategy for a class of indefinite affine-qudratic stochastic differential games[J]. Journal of Guangdong University of Tcehnology, 2012, 29(3): 35-38. |
| [16] |
张成科, 植璟涵, 朱怀念. 合作博弈、匹配理论与市场设计实践及其政策启示——2012年诺贝尔经济学奖得主的主要研究贡献述评[J].
广东工业大学学报:社会科学版, 2013, 13(1): 13-18.
Zhang C K, Zhi J H, Zhu H N. The practice and policy implications of cooperative game, matching theory and market design[J]. Journal of Guangdong Universsity of Tcehnology:Social Sciences Edition, 2013, 13(1): 13-18. |
 2015, Vol. 32
2015, Vol. 32