近年来,声子晶体由于拥有丰富的物理内涵和广阔的应用前景而受到国内外学者的广泛关注.声子晶体是指具有弹性波(声波)带隙特性的周期性复合材料或结构.它是一种新型的人工结构功能材料,通过设计可以人为地调控声波或弹性波的频率和方向,从而实现对声波或弹性波传输的控制,因此在现实中有许多应用,例如:利用声子晶体缺陷态设计新型的高效滤波器[1]、高效声波谐振器和波导[2-6]、利用声子晶体负折射性质设计声超透镜[7]、利用高态密度通带设计吸声材料[8]等等.研究和完善声子晶体理论有着重要的意义.
已有研究发现,当声子晶体中存在缺陷时,原始的带隙范围内会产生缺陷带,缺陷带频率范围内的弹性波或声波只能被局域在缺陷处或沿着缺陷传播[9-15].吴福根等人[9-11]研究了缺陷的填充率、方向和几何结构对二维水圆柱体按正方晶格排列平行放置在水银基体的缺陷模的影响.Khelif等人[14]研究了弯曲线缺陷声子晶体中弹性波的传播,结果表明弹性波能够沿着线缺陷方向传播.同时该课题组研究了由铝氮化物棒放在铅/环氧树脂系统中形成棒缺陷的波导模,提出传播模沿着棒缺陷能够被局域在声子晶体带隙中.近来,Wu等人[16-17]通过在声子晶体腔中放置压电弯曲梁这种方法设计了一种声能俘获系统,入射声波的频率与腔体共振频率一致时,能够实现声能俘获.Lü等人[18]从一个完美声子晶体中移除一根棒形成一个共振腔,这个结构能够同时实现阻尼减振和宽分布振动的能量俘获.但是,已设计系统俘获能量的能力和转化效率都非常低,限制了其应用.如何提高声能的聚集能力和转化效率,成为了声子晶体声能俘获系统应用的关键问题.
声能的聚集能力和转化效率与声子晶体中缺陷的性质和压电片的结构以及放置位置有着至关重要的关系.最近,赵言诚等人[19]研究了一类由三组元材料形成的线缺陷,结果表明将三组元材料形成线缺陷引入到二组元声子晶体中,在原来的带隙中将会出现传导模.受此思路的启发,本文研究了由水圆柱体插在水银基体中,组成具有点缺陷声子晶体,并将一定结构的压电片放入其中收集声能.采用类似的在点缺陷中引入第三组元的优化方法,计算寻找高质点速度场,预知压电片最优的位置和结构,获得了最优的声能俘获系统,并发现低密度的缺陷圆柱体在高密度流体基体下更利于声波局域和声能俘获.
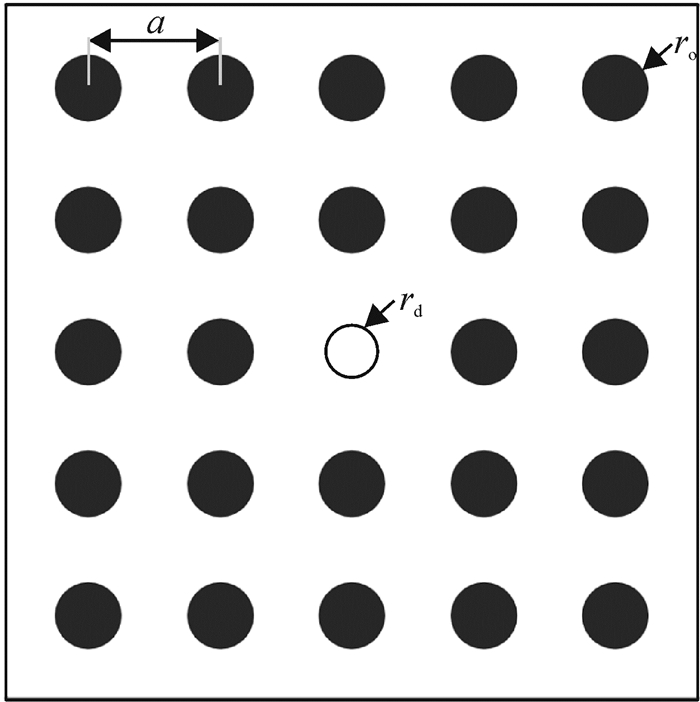
1 模型本文研究的二维声子晶体结构模型,由水圆柱体按正方晶格排列平行放置在水银中组成,材料参数:水散射体密度ρ为1.0×103 kg/m3, 纵波波速Cl为1.48 km/s;水银基体密度ρ为13.5×103 kg/m3, 纵波波速Cl为1.45 km/s.在图 1中,通过改变在5×5超元胞中心柱体的材料和半径来引入缺陷.a为晶格常数, r为圆柱体半径.为了计算压力场和质点加速度场,本文采用有限元(COMSOL Multiphysics)结合超元胞方法.
|
图 1 二维声子晶体点缺陷的截面图. Figure 1 The cross section of the point defect inside the two-dimensional phononic crystal |
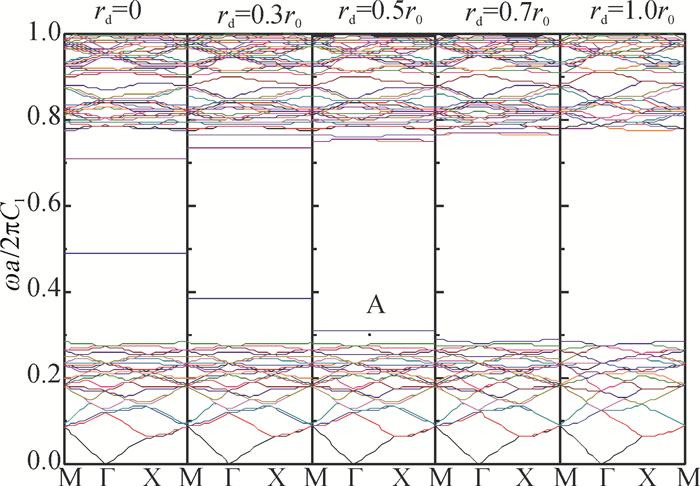
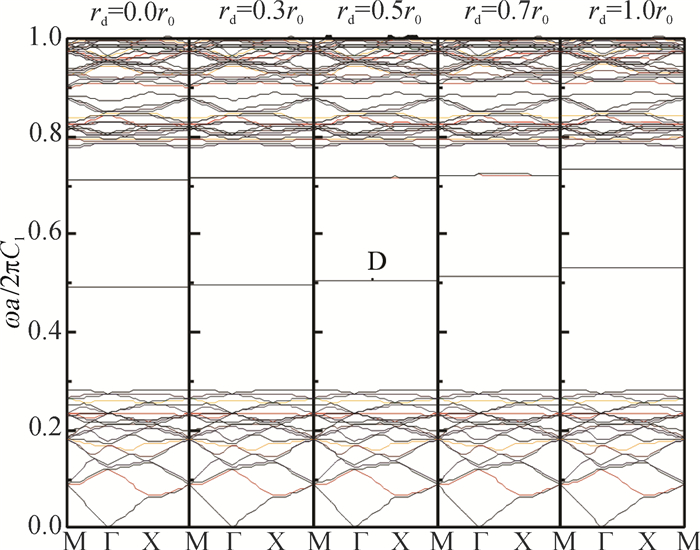
首先,考虑缺陷圆柱体是由不同半径的水圆柱体构成.图 2给出了计算得到的不同半径的缺陷水圆柱体声子晶体色散关系图.其余水圆柱体半径r0是0.31a,所对应的填充率f为0.3.缺陷圆柱的半径是逐渐变化的.当rd= r0(r0= 0.31a)时,发现在归一化频率(ωa/2πC1)在0.278到0.755之间有一条宽带隙.缺陷带开始从带隙的上下两个边缘出现,随着rd的减小,它们向带隙的中间移动.当rd= 0时,两条明显的缺陷带出现在带隙中间频率段.通过进一步研究发现,这归一化频率为0.713的缺陷模是一个双重简并模.这一结果与课题组早期用平面波展开法研究的结果一致[13].
|
图 2 由水圆柱体散射体插在水银基体组成的缺陷系统的声子晶体能带结构图 Figure 2 The phononic band structure of defect system consisting of water cylinders in mercury background |
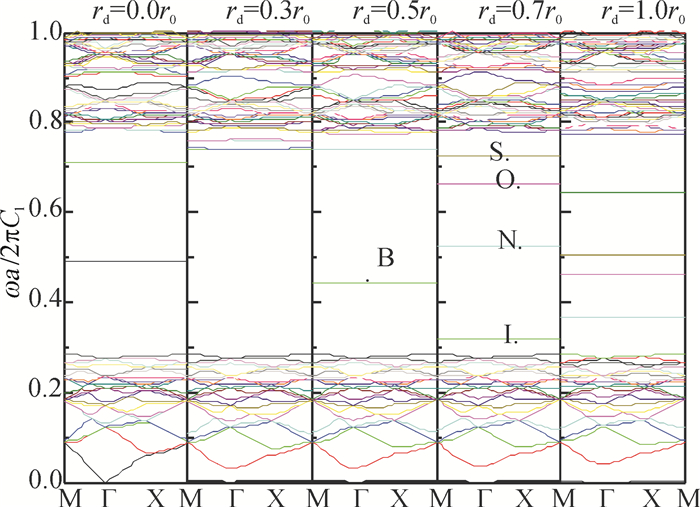
图 3为缺陷圆柱体的声子晶体能带结构图,其中缺陷圆柱体是由空气组成的,而其他圆柱体仍然是水圆柱体.空气的参数是ρ=1.29kg/m3, C1为0.34 km/s.可以发现缺陷带的变化趋势不同于水缺陷圆柱体.当缺陷圆柱体为空气时,带隙里面出现更多的缺陷带.随着半径rd增加,将有更多的缺陷带落在带隙中,同时发现缺陷带向下移动,但是当缺陷圆柱体为水时,两条缺陷带分别向带隙上下边界移动,最后消失在带隙里.通过Wu[17-18]等人放置最优的压电材料在声波局域的地方, 将能够获得多频率声能俘获系统.
|
图 3 空气缺陷圆柱体声子晶体的能带结构图 Figure 3 The band structure of the phononic crystal with air defect cylinder |
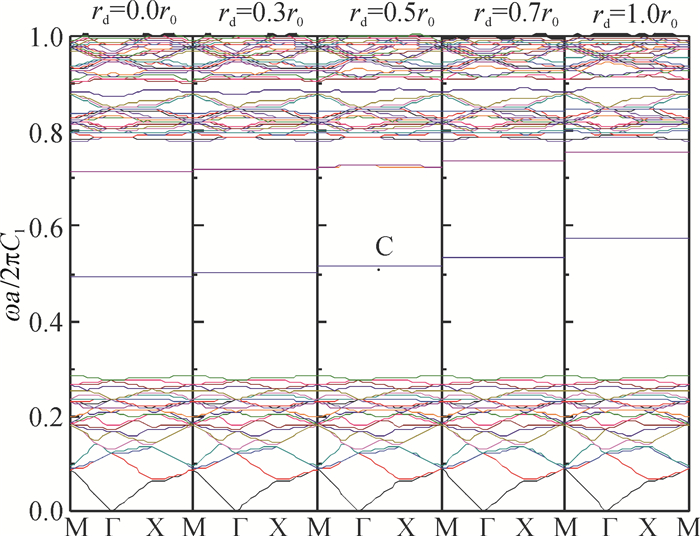
因为缺陷圆柱体的性能对缺陷带有很大的影响,于是本文进一步用铁和铅来做缺陷圆柱体,其他仍然是水圆柱体.铁和铅的密度都远大于水.图 4和图 5中分别给出了两类缺陷的能带结构图.发现这两个能带结构图中都出现两条缺陷带.当点缺陷的半径增大的时候,缺陷带仅仅朝上移动一点.比较图 4和图 5,发现两者的缺陷带变化趋势十分相似.这是由于弹性波通过大密度的固体缺陷圆柱体将很难被散射,产生的缺陷模主要依赖于缺陷圆柱体的大小.然而,弹性波在低密度流体缺陷圆柱体系统中具有很强的散射,从而产生很多缺陷带.
|
图 4 铁缺陷圆柱体的声子晶体能带结构图 Figure 4 The band structure of the phononic crystal with defect iron cylinder |
|
图 5 铅缺陷圆柱体的声子晶体能带结构图 Figure 5 The phononic band structure of the phononic crystal with defect lead cylinder |
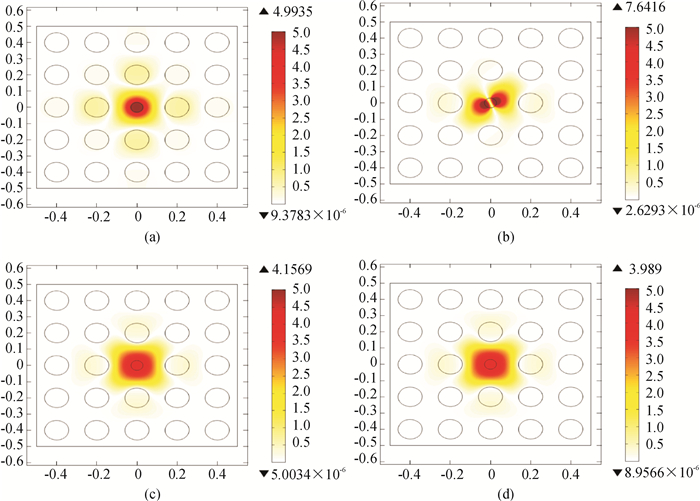
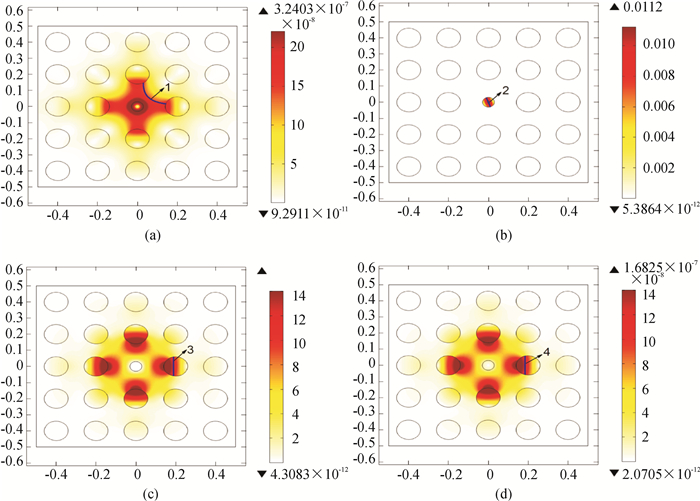
参考文献[16-17],压电材料的结构和放置位置通过缺陷模的压力场和质点加速度场来确定.图 6和图 7为Γ附近缺陷模的压力场和质点加速度场分布图,分别描述了图 2~图 5中模A, B, C, D情况, 缺陷圆柱半径rd=0.5r0, 晶格常数设为0.2 m.所有的模都显示出局域现象,意味着在点缺陷附近声能被俘获.当缺陷材料是空气时,能够看到最大的压力值和最大质点加速度值分别是7.64 Pa和0.0 112 m/s,能量分布集中.模A压力振幅最大值是模D压力振幅最大值的1.9倍,质点加速度是其105倍.因此,得出压力最大值就是质点加速度最小值这个关系.该结果与固体棒插在空气中组成的缺陷系统结果一致.理论上,如果压电材料放置在高质点速度场的位置,局部应变将使压电材料工作,从而将振动的能量转化为电能.压电片的形状和放置位置如图 7中标注1、2、3和4所示.压电片1是弧形形状,其他的是条形形状.压力越大,声能转化和俘获就越多.综上所述,可知,低密度缺陷圆柱体插入高密度流体基体更有利于俘获声能.
|
图 6 压力场的振幅分布图 Figure 6 The of amplitude of pressure fields |
|
图 7 质点速度场分布图 Figure 7 The particle velocity fields |
因为空气缺陷圆柱体有利于俘获声能,于是笔者计算了缺陷模的质点加速度场.图 8为标注在图 3中rd = 0.7r0能带结构中I、N、O、和S点缺陷模的质点加速度.这些缺陷模场是双重简并模.压电材料一定要放置在高质点速度场的位置.当归一化频率为0.319、0.525或者0.661时,压电片应该放置在空气圆柱体里.当归一化频率是0.723时,压电片应该放置在点缺陷周围的水圆柱体里.通过分析,这样的结果能够获得多频率声能俘获系统.

|
图 8 缺陷模在Γ点的质点加速度场 Figure 8 The particle velocity fields of defect modes near Γ point |
本文研究了二维点缺陷声子晶体的声能俘获系统的优化,这种声子晶体是由水圆柱体散射体插入水银基体组成的.本文在二维声子晶体里通过引入第三组元点缺陷提供了一种优化声能俘获的方法.通过分析高对称点缺陷模的压力场和质点速度场,获得压电片最优的位置和结构.压电片应该放置在高质点速度场,压电片振动是通过质点的振动产生的.本文发现低密度缺陷材料在高密度基体里更利于俘获声能, 当缺陷材料为空气时,大量的缺陷带落在带隙中,可应用于设计多频率声能俘获系统.
| [1] |
Pennec Y, Djafari-Rouhani B, Vasseur J O, et al. Tunable filtering and dem-ultiplexing in phononic crystals with hollow cylinders[J].
Physical Review E, 2004, 69(4): 046 608(1-6).
|
| [2] |
Psarobas I E, Stefanou N, Modinos A. Scattering of elastic waves by periodic arrays of spherical bodies[J].
Physical Review B, 2000, 62(1): 278-291.
DOI: 10.1103/PhysRevB.62.278. |
| [3] |
Wu T T, Hsu J C, Sun J H. Phononic plate waves[J].
IEEE Transactions On Ultrasonics Ferroelectrics And Frequency Control, 2011, 58(10): 2146-2161.
DOI: 10.1109/TUFFC.2011.2064. |
| [4] |
Hsu F C, Hsu J C, Huang T C, et al. Reducing support loss in micromechanicalring resonators using phononic band-gap structures[J].
Journal of Physics D: Applied Physics, 2011, 44(37): 375101.
DOI: 10.1088/0022-3727/44/37/375101. |
| [5] |
Mohammadi S, Eftekhar A A, Hunt W D, et al. High-Q micromechanical resonators in a two dimensional phononic crystal slab[J].
Applied Physics Letters, 2009, 94(5): 051906.
DOI: 10.1063/1.3078284. |
| [6] |
Wu T C, Wu T T, Hsu J C. Waveguiding and frequency selection of Lamb waves in a plate with a periodic stubbed surface[J].
Physical Review B, 2009, 79(10): 104306.
DOI: 10.1103/PhysRevB.79.104306. |
| [7] |
Yuuki K, Kenji T, Kazuhiro F, et al. Negative refraction and energy transmission efficiency of acoustic waves in two-dimensional phononic crystal: numerical and experimental study[J].
Japanese Journal of Applied Physics, 2011, 50(6): 067301.
DOI: 10.1143/JJAP.50.067301. |
| [8] |
Zhao H G, Liu Y Z, Yu D L, et al. Absorptive properties of three-dimensional phononic crystal[J].
Journal of Sound and Vibration, 2007, 303(1-2): 185-194.
DOI: 10.1016/j.jsv.2007.01.004. |
| [9] |
Wu F G, Liu Z Y, Liu Y Y. Splitting and tuning characteristics of the point defect modes in two-dimensional phononic crystals[J].
Physical Review E, 2004, 69(6): 066609.
DOI: 10.1103/PhysRevE.69.066609. |
| [10] |
He Y, Wu F G, Yao Y W, et al. Effect of defect configuration on the localization of phonons in two-dimensional phononic crystals[J].
Physics Letters A, 2013, 377(12): 889-894.
DOI: 10.1016/j.physleta.2013.02.001. |
| [11] |
钟兰花, 吴福根, 彭程万. 二维点缺陷声子晶体中缺陷填充率对能带的影响[J].
应用声学, 2009, 28(2): 140-146.
Zhong L H, Wu F G, Peng C W. The influence of defect filling fraction on the energy band in 2D point defect phononic crystals[J]. Applied Acoustics, 2009, 28(2): 140-146. DOI: 10.11684/j.issn.1000-310X.2009.02.012. |
| [12] |
Lucklum R, Ke M Z, Zubtsov M. Two-dimensional phononic crystal sensor based on a cavity mode[J].
Sensors Actuators B, 2012, 171: 271-277.
|
| [13] |
Zhang X, Liu Z Y, Liu Y Y, et al. Defect states in 2D acoustic band-gap materials with bend-shaped linear defects[J].
Solid State Communications, 2004, 130(1-2): 67-71.
DOI: 10.1016/j.ssc.2004.01.007. |
| [14] |
Khelif A, Djafari-Rouhani B, Vasseur J, et al. Transmittivity through straight and stublike waveguides in a two-dimensional phononic crystal[J].
Physical Review B, 2002, 65(17): 174308.
DOI: 10.1103/PhysRevB.65.174308. |
| [15] |
Khelif A, Choujaa A, Djafari-Rouhani B, et al. Trapping and guiding of acoustic waves by defect modes in a full-band-gap ultrasonic crystal[J].
Physical Review B, 2003, 68(21): 214301.
DOI: 10.1103/PhysRevB.68.214301. |
| [16] |
Wu L Y, Chen L W, et al. Acoustic energy harvesting using resonant cavity of a sonic crystals[J].
Applied Physics Letters, 2009, 95(1): 013506.
DOI: 10.1063/1.3176019. |
| [17] |
Wang W H, Wu L Y, Chen L W, et al. Acoustic energy harvesting by piezoelectric curved beams in the cavity of a sonic crystal[J].
Smart Materials and Structures, 2010, 19(4): 045016.
DOI: 10.1088/0964-1726/19/4/045016. |
| [18] |
Lü H Y, Li D C, Tian X Y, et al. Vibration energy harvesting using a phononic crystal with point defect states[J].
Applied Physics Letters, 2013, 102(3): 034103.
DOI: 10.1063/1.4788810. |
| [19] |
Zhao Y C, Deng L Z, Yuan L B. Characteristics of the guided modes in a two-dimensional three-component phononic crystal with linear defects[J].
Physica Scripta, 2012, 85(2): 025401.
DOI: 10.1088/0031-8949/85/02/025401. |
 2015, Vol. 32
2015, Vol. 32