Dr.Bridge是一个集可视化数据处理、数据库管理、结构分析为一体的综合性桥梁结构有限元计算系统.一般桥梁结构, 有几百甚至几万个单元^[1-4], 数据量庞大, 逐一输入单元信息实不可取.在Dr.Bridge建模中, 除一些特殊单元外, 通常使用快速编辑器完成大部分单元的编辑, 可以减轻输入的工作量.Dr.Bridge系统在输入单元信息界面上, 提供了直线、拱肋、拉索、平行、对称、平移、内插、单元、截面、坐标等10余种单元快速编辑器, 用户可根据实际情况, 选取最快捷的输入方式.其中, 直线编辑器可快速编辑连成1条直线的多个单元信息, 生成单元的顶缘或截面的高度中点位于同1条直线上的一组单元组.利用直线快速编辑器, 系统将打开如图 1所示的对话框, 用户需在界面内定义控制断面, 并选择各控制点处控制断面的截面拟合类型, 其它截面可由已经定义好的控制断面经直线内插或按抛物线拟合而成.

图 1(Figure 1)

图 1 直线单元组编辑器界面 Figure 1 Linear editor interface

Dr.Bridge系统使用手册指出^[5]:利用直线快速编辑器进行二次抛物线拟合时, 二次抛物线需由3点确定, 第1点的截面拟合类型不限制, 第2点的截面拟合类型必须选择图 1中“向后抛物线”, 第3点的类型必须选择“向前抛物线”.这样, 程序将以此3点为控制点, 拟合出1条二次抛物线.然而, 在利用直线快速编辑器建模时, 通常会遇到已知两点来确定一条抛物线的情况^[6].此时, 只定义了两个控制断面, 如何依此两个控制点来拟合出1条二次抛物线, Dr.Bridge系统使用手册并未给出此种情况下抛物线的拟合方法.

实际上, 人机界面技术的开发, 有利于提高建模效率^[7-10].函数的单调性及凸凹性与其所表示曲线的局部性态存在一定的规律^[11-14].本文通过考虑曲线单调性及凸凹性等性态符号, 提出在Dr.Bridge建模中利用直线快速编辑器准确判定抛物线拟合方向的新方法, 对于无论已知两控制点还是已知三控制点情况, 该方法均能准确识别抛物线拟合方向.以三跨变截面连续箱梁的建模实例进一步验证了本文方法的简捷性和高效性.

函数的单调性及凸凹性是函数的局部性态和重要性质^[15].二次抛物线在单调区间内, 可通过考查其凸凹性, 来确定二次抛物线的局部性态, 从而判定抛物线在单调区间内的曲线拟合方向.

利用直线快速编辑器进行二次抛物线拟合时, 多数情况下会遇到仅在两处定义了控制断面, 第1点(起点)的截面拟合类型不限制.而第2点(终点)的截面拟合类型究竟选择图 1中的“向前抛物线”还是“向后抛物线”, Dr.Bridge系统使用手册对这种情况未提及, 一直是建模过程中的技术难点.实际上, 由两控制点拟合1条二次抛物线情况, 考查抛物线的单调性及凸凹性, 只会出现如图 2所示的4种性态.

图 2(Figure 2)

图 2 两控制点抛物线的性态 Figure 2 Parabola shapes fitted by two controlling points

定义1  设二次抛物线f(x)经单调区间内两点x₁和x₂拟合而成, 若满足关系式(1), 如图 2(a)、2(b)所示(或关系式(2), 如图 2(c)、2(d)所示), 则称f(x)在[x₁, x₂]上是凸的(或凹的).

定理1   引入两套符号:第1套符号为抛物线单调性记号, 第2套符号为抛物线凸凹性记号.在第1套符号标识中, 若第1点(起点)到第2点(终点)为单调递减函数, 记号为⊕;若第一点(起点)到第2点(终点)为单调递增函数, 记号为㊀.在第2套符号标识中, 若抛物线是凸的, 记号为⊕;反之为㊀.那么, 若两套符号同号, 则第2点(终点)截面拟合类型为“向前抛物线”; 若两套符号异号, 则第2点(终点)截面拟合类型为“向后抛物线”.

根据定义1和定理1, 对图 2所示的基于两控制点抛物线可能出现的4种情形, 表 1给出了由两控制点判定抛物线拟合方向的全过程.

表 1(Table 1)

表 1 两控制点抛物线截面拟合类型的判定 Table 1 Identification of parabola fitting type by two controlling points 抛物线性态 第1套符号 第2套符号 终点截面拟合类型 (a) ⊕ ⊕ “向前抛物线” (b) ㊀ ⊕ “向后抛物线” (c) ⊕ ㊀ “向后抛物线” (d) ㊀ ㊀ “向前抛物线”

表 1 两控制点抛物线截面拟合类型的判定 Table 1 Identification of parabola fitting type by two controlling points

在1条二次抛物线由三控制点确定的情况下, 对抛物线拟合方向的判定, 本文考虑单调性及凸凹性的抛物线拟合方法仍然适用.这时, 首先考查抛物线的单调性, 将抛物线分为前半段(第1点至第2点)和后半段(第2点至第3点), 如图 3所示, 其中间点(第2点), 在前半段视为曲线的终点, 在后半段视为曲线的起点.然后在前半段和后半段分别运用定理1来判定本段抛物线终点截面拟合类型.表 2给出了由三控制点判定抛物线拟合方向的全过程.

图 3(Figure 3)

图 3 三控制点抛物线的性态 Figure 3 Parabola shapes by three controlling points

表 2(Table 2)

表 2 三控制点抛物线截面拟合类型的判定 Table 2 Identification of parabola fitting type by three controlling points 抛物线性态 第1套符号 第2套符号 终点截面拟合类型 (a) 前半段 ㊀ ⊕ 第2点“向后抛物线” 后半段 ⊕ ⊕ 第3点“向前抛物线” (a) 前半段 ⊕ ㊀ 第2点“向后抛物线” 后半段 ㊀ ㊀ 第3点“向前抛物线”

表 2 三控制点抛物线截面拟合类型的判定 Table 2 Identification of parabola fitting type by three controlling points

Dr.Bridge系统使用手册指出:二次抛物线需由3点确定, 第1点的截面拟合类型不限制, 第2点的拟合类型必须是“向后抛物线”, 第3点的类型必须是“向前抛物线”.这样, 程序将以此3点为控制点, 拟合出1条二次抛物线.由表 2可以看出, 本文判定结果与Dr.Bridge系统使用手册给出的结论完全一致, 这说明本文方法对3点情况仍然适用.

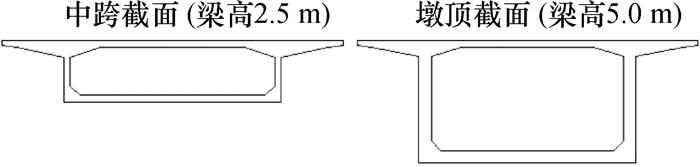
三跨连续梁跨径布置为30 m+40 m+30 m，共100 m.边跨、中跨合拢段、墩部位置均有一段直线段, 边跨墩部和中跨合拢段直线段分别为10 m, 4 m和2 m.拟定模型共分100个单元, 每单元为1 m, 如图 4所示.控制断面形状如图 5所示, 为铅直腹板单箱单室, 边跨和中跨梁高为2.5 m, 墩顶梁高为5.0 m.

图 4(Figure 4)

图 4 三跨连续梁单元划分示意 Figure 4 Element arrangement of three-span continuous box girder

图 5(Figure 5)

图 5 控制断面形状 Figure 5 Configurations of controlling sections

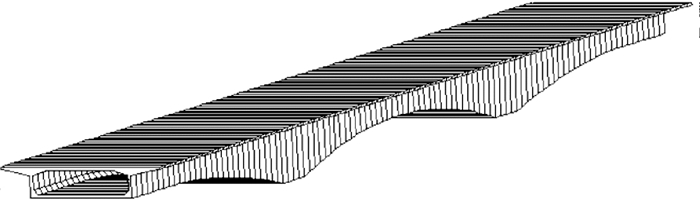
由图 4知, 单元顶缘在同一直线上, 梁底缘线可用直线内插和抛物线拟合, 选用直线快速编辑器可完成模型的建立.在图 1所示的界面内, 控制点距起点距离这一栏, 依次添加0、10、28、32、49、51，68，72，90，100共10个控制断面, 输入各控制断面的尺寸, 确定各截面拟合类型.运用本文两控制点抛物线截面拟合类型的判定方法, 依次选择0 m处:直线内插; 10 m处:直线内插; 28 m处:向前抛物线; 32 m处:直线内插; 49 m处:向后抛物线; 51 m处:直线内插; 68 m处:向前抛物线; 72 m处:直线内插; 90 m处:向后抛物线; 100 m处:直线内插.如图 6所示.至此, 利用直线快速编辑器在10个控制断面处经直线或抛物线拟合, 建立了跨径为100 m的三跨变截面连续箱梁模型, 如图 7所示.

图 6(Figure 6)

图 6 控制断面截面拟合类型界面 Figure 6 Linear editor of parabola fitting type

图 7(Figure 7)

图 7 三跨连续梁三维模型图 Figure 7 Model of three-span continuous box girder

通过考查二次函数的单调性及凸凹性, 给出了由两控制点拟合的抛物线4种性态.在此基础上, 引入表征抛物线性态的两套符号, 提出抛物线截面拟合类型的判定方法, 拓展了Dr.Bridge直线快速编辑器由两控制点准确拟合抛物线的新途径.本文提出的考虑函数单调性及凸凹性的抛物线拟合方法, 无论对由两控制点还是由三控制点来拟合1条抛物线情况, 都能准确识别抛物线拟合方向.本文方法操作简捷、易于程序实现, 大大提高了建模的效率.