摄像机标定是实现三维重建和高精度测量的关键技术之一.在众多的摄像机标定方法当中,基于棋盘格平面模板的摄像机标定由于其标定模板制作简单,精度可以满足要求,得到了广泛应用[1].该方法主要是通过建立棋盘格角点坐标与对应点的世界坐标关系来确定摄相机的参数,最终完成摄像机的标定[1-3].
目前测量系统标定方法一般包括平行度、垂直度、物面与成像间的比例关系和系统几何参数的标定等几个方面.但是从标定实际应用状况和结果来看,有时候会产生标定精度不高,标定系统不稳定,标定操作过程复杂、繁琐、耗时等缺点,导致标定效果并不理想.
本文提出一种基于棋盘格标定板结合二维手动导轨平台的高精度单目摄像机标定方法.该方法操作简单、快速且稳定性好,能够有效获取高精度摄像机参数,可满足三维重建和其他视觉检测场合使用要求.
1 棋盘格亚像素角点坐标提取 1.1 图像获取实验系统构成如下:高精度Kodak(柯达)ES 1.0 CCD相机、铝合金多维度调整桁架、二维手动导轨平台(行程0~180 mm,精度±0.01 mm),方格数为11×11棋盘格标定板(精度±1~3 μm).实验装置实物如图 1所示.

|
图 1 系统装置图 Figure 1 System device |
本文使用的方法以DLT标定法(直接线性标定法)为基础,该方法需要对棋盘格标定模板进行多次拍摄,得到一系列z值的棋盘格标定模板图像,以准确提取棋盘格亚像素角点坐标, 具体操作如下:
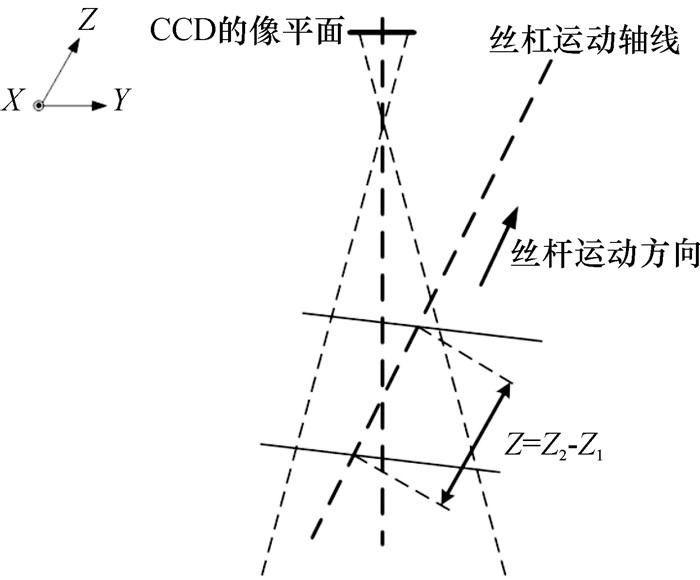
利用高精度CCD摄像机对放置在二维手动导轨平台的棋盘格标定板进行拍摄.把CCD相机聚焦在Z =150 mm处,对焦完毕后重新把标尺摇回到原点处,在允许的景深范围内沿Z轴方向(丝杆运动方向)在0~100 mm范围内每隔10 mm对棋盘格标定板拍摄一次,共拍摄11幅棋盘格图片.拍摄原理如图 2所示.
|
图 2 系统拍摄原理图 Figure 2 Principles of shooting system |
拍摄得到棋盘格图像如图 3所示.

|
图 3 标定拍摄棋盘图像 Figure 3 Calibration checkerboard image |
常用的平面标定模板一般是黑白棋盘或者离散的正方形[4-8].模板图像的角点提取算法一般分为从模板图像提取直线求直线交点和基于图像灰度的角点检测方法两大类.本文角点提取是基于第二类方法,即先进行Harris角点检测,再用基于梯度搜索的方式精确控制角点的位置,从而得到精确的亚像素角点坐标[9-10].
Harris算子[10-11]是Harris和Stephens在1988年提出的一种静态图像的点特征提取算子.Harris算子把信号处理中的自相关函数矩阵的特征值看作自相关函数的一阶曲率,即对于图像中的任意一点,如果它的水平和垂直曲率均高于局部区域中的其他点,则认为该点是特征点.该算子能够在图像旋转、灰度、噪声影响和视点转换条件下简单有效地提取点特征,同时又相对于其他特征提取算子稳定[12].Harris算子表达式如下:
| $ I = \det \left( C \right) - k \times {\rm{t}}{{\rm{r}}^2}\left( C \right), $ | (1) |
其中I表示每个兴趣点的值,det为矩阵行列式,k为经验值, 一般取0.04,tr为矩阵的迹,C可以表示为
| $ C\left( {i,j} \right) = G\left( s \right) \otimes \left[ {\begin{array}{*{20}{c}} {g_x^2}&{{g_x}{g_y}}\\ {{g_x}{g_y}}&{g_y^2} \end{array}} \right]. $ | (2) |
其中G (s)为高斯模板,gx为x方向的梯度,gy为y方向的梯度.在提取特征点时,若某一像素点的兴趣值大于某一阈值T,则可认为该像素点是特征点.
利用Harris算子找到像素级的角点位置后,为更精确地提取角点坐标,需要进一步利用基于梯度搜索的方式精确控制点的位置.
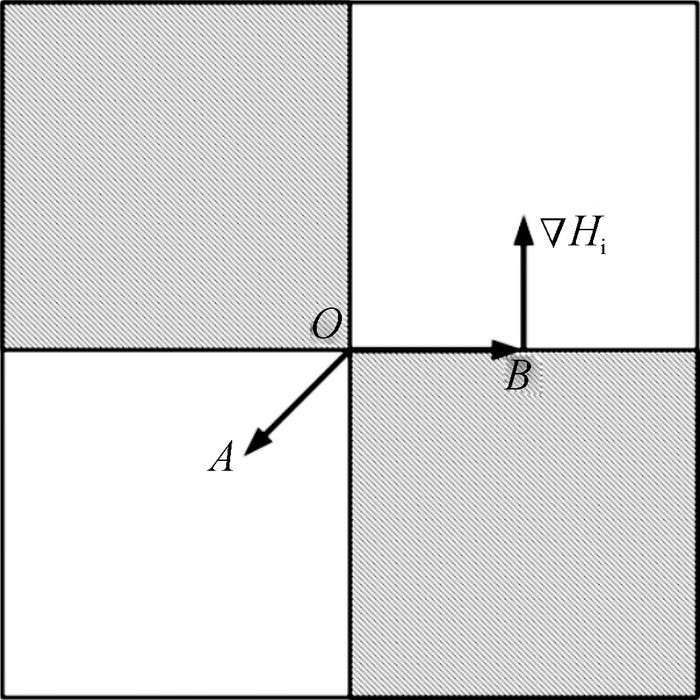
如图 4所示,棋盘格角点附近的点可以分为在边缘上的点和不在边缘上的点.A点代表不在边缘上的点,该点处的灰度梯度为0;B点代表在边缘上的点,该点处的灰度梯度▽Hi与
|
图 4 棋盘格灰度梯度示意图 Figure 4 Gray gradient of checkerboard |
在边缘上的点与其灰度梯度的关系为
| $ \nabla H_i^T \cdot \left( {\vec \alpha - \vec \beta } \right) = 0, $ | (3) |
式中,▽ HiT为灰度梯度向量,
实际上,图像往往会受噪声影响,因此一般情况下式(3)不为0,需要将其转化为求误差和S最小的问题,方程具体如下:
| $ S = \sum\limits_i \theta = \sum\limits_i {\nabla H_i^T} \cdot \left( {\vec \alpha - \vec \beta } \right). $ | (4) |
再对式(4)进行一系列变换可以得到图 4中角点O的迭代式:
| $ \sum\limits_i {\nabla H_i^k} \cdot \nabla H_i^{{k^T}} \cdot {{\vec \alpha }^{k + 1}} = \sum\limits_i {\nabla H_i^k} \cdot \nabla H_i^{{k^T}} \cdot \vec \beta . $ | (5) |
通过对式(5)迭代可以得到更精确的亚像素角点坐标.
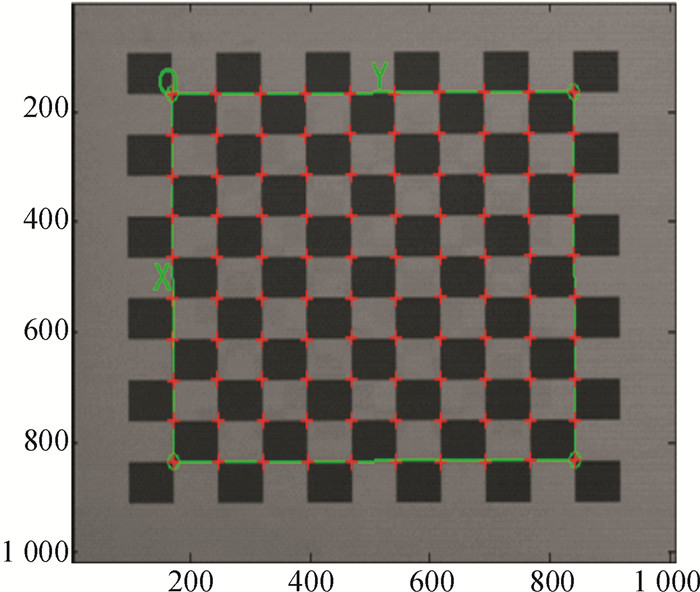
棋盘格图像提取到的亚像素角点坐标如图 5所示.
|
图 5 棋盘格角点提取图像 Figure 5 Checkerboard corner extraction image |
摄像机标定首先要确定摄像机模型,本文中的摄像机模型以理想的针孔成像模型为基础.由于在标定过程中使用了高精度CCD相机结合二维手动导轨平台对棋盘格进行拍摄,且在Z坐标方向进行不同位置的拍摄是静止的,所以在这个过程中产生的径向畸变和切向畸变很小.在不考虑畸变的前提下利用DLT标定法来确定摄像机参数.
首先确定摄像机模型定义的各个坐标之间的转换关系,世界坐标系与摄像机坐标系之间变换如下:
| $ \left[ {\begin{array}{*{20}{c}} {{X_{ci}}}\\ {{Y_{ci}}}\\ {{Z_{ci}}}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{R}}&\mathit{\boldsymbol{T}}\\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_{wi}}}\\ {{Y_{wi}}}\\ {{Z_{wi}}}\\ 1 \end{array}} \right], $ | (6) |
其中
根据摄像机针孔成像模型,由世界坐标系到图像像素坐标系转换如下:
| $ \begin{array}{l} {Z_{ci}}\left[ {\begin{array}{*{20}{c}} {{u_i}}\\ {{v_i}}\\ 1 \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{\rm{d}}x}}}&\lambda &{{u_0}}\\ 0&{\frac{1}{{{\rm{d}}y}}}&{{v_0}}\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} f&0&0&0\\ 0&f&0&0\\ 0&0&1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{R}}&\mathit{\boldsymbol{T}}\\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_{wi}}}\\ {{Y_{wi}}}\\ {{Z_{wi}}}\\ 1 \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {{f_x}}&0&{{u_0}}&0\\ 0&{{f_y}}&{{v_0}}&0\\ 0&0&1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{R}}&\mathit{\boldsymbol{T}}\\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_{wi}}}\\ {{Y_{wi}}}\\ {{Z_{wi}}}\\ 1 \end{array}} \right] = {\mathit{\boldsymbol{M}}_1}{\mathit{\boldsymbol{M}}_2}\left[ {\begin{array}{*{20}{c}} {{X_{wi}}}\\ {{Y_{wi}}}\\ {{Z_{wi}}}\\ 1 \end{array}} \right] = \\ \mathit{\boldsymbol{M}}\left[ {\begin{array}{*{20}{c}} {{X_{wi}}}\\ {{Y_{wi}}}\\ {{Z_{wi}}}\\ 1 \end{array}} \right], \end{array} $ | (7) |
其中, fx = f / dx,fy = f / dy为尺度因子;u0,v0为图像中心坐标;λ为两坐标轴间倾斜因子;M1由摄像机内部参数fx,fy,u0,v0决定,M2由外部参数R,T决定,M为投影矩阵.
将式(7)进行简化,得到式(8):
| $ {Z_{ci}}\left[ {\begin{array}{*{20}{c}} {{u_i}}\\ {{v_i}}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{m_{11}}}&{{m_{12}}}&{{m_{13}}}&{{m_{14}}}\\ {{m_{21}}}&{{m_{22}}}&{{m_{23}}}&{{m_{24}}}\\ {{m_{31}}}&{{m_{32}}}&{{m_{33}}}&{{m_{34}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_{wi}}}\\ {{Y_{wi}}}\\ {{Z_{wi}}}\\ 1 \end{array}} \right], $ | (8) |
其中(ui, vi)为提取得到的第i个角点亚像素坐标,(Xwi, Ywi, Zwi)为第i个与角点亚像素坐标对应的空间坐标,该坐标可以通过棋盘格标定板方格尺寸大小来获得.
式(8)展开后可以得到每个角点所对应的两个关于mij的线性方程:
| $ \begin{array}{l} {X_{wi}}{m_{11}} + {Y_{wi}}{m_{12}} + {Z_{wi}}{m_{13}} + {m_{14}} - {u_i}{X_{wi}}{m_{31}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{u_i}{Y_{wi}}{m_{32}} - {u_i}{Z_{wi}}{m_{33}} = {u_i}{m_{34}}. \end{array} $ | (9) |
| $ \begin{array}{l} {X_{wi}}{m_{21}} + {Y_{wi}}{m_{22}} + {Z_{wi}}{m_{23}} + {m_{24}} - {v_i}{X_{wi}}{m_{31}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{v_i}{Y_{wi}}{m_{32}} - {v_i}{Z_{wi}}{m_{33}} = {v_i}{m_{34}}. \end{array} $ | (10) |
由式(9)和(10)可知,若棋盘格标定有n个已知亚像素角点坐标(ui, vi),i = 1~ n,及其对应的空间坐标(Xwi, Ywi, Zwi),i = 1~ n,则可以得到2n个关于M矩阵的线性方程,如下:
| $ \begin{array}{*{20}{l}} \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{X_{w1}}}&{{Y_{w1}}}&{{Z_{w1}}}&1&0&0&0&0&{ - {u_1}{X_{w1}}}&{ - {u_1}{Y_{w1}}}&{ - {u_1}{Z_{w1}}}\\ 0&0&0&0&{{X_{w1}}}&{{Y_{w1}}}&{{Z_{w1}}}&1&{ - {v_1}{X_{w1}}}&{ - {v_1}{X_{w1}}}&{ - {v_1}{X_{w1}}}\\ {}& \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots &{}\\ {}& \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots &{}\\ {{X_{wn}}}&{{Y_{wn}}}&{{Z_{wn}}}&1&0&0&0&0&{ - {u_n}{X_{wn}}}&{ - {u_n}{X_{wn}}}&{ - {u_n}{X_{wn}}}\\ 0&0&0&0&{{X_{wn}}}&{{Y_{wn}}}&{{Z_{wn}}}&1&{ - {u_n}{X_{wn}}}&{ - {u_n}{X_{wn}}}&{ - {u_n}{X_{wn}}} \end{array}} \right]\\ \times \left[ {\begin{array}{*{20}{c}} {{m_{11}}}&{{m_{12}}}&{{m_{13}}}&{{m_{14}}\;\;\;\;{{\left. {\begin{array}{*{20}{c}} {{m_{21}}}&{{m_{22}}}&{{m_{23}}}&{{m_{24}}}&{{m_{31}}}&{{m_{32}}}&{{m_{33}}} \end{array}} \right]}^{\rm{T}}}} \end{array}} \right. \end{array}\\ { = {{\left[ {\begin{array}{*{20}{c}} {{u_1}{m_{34}}}&{{v_1}{m_{34}}}& \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots &{{u_n}{m_{34}}}&{{v_n}{m_{34}}} \end{array}} \right]}^{\rm{T}}}.} \end{array} $ | (11) |
从式(11)中可知M矩阵乘以任意不为0的常数并不影响(ui, vi)与(Xwi, Ywi, Zwi)之间的关系,因此可以指定m34=1,并且通过式(11)中的2n个线性方程可以求得M矩阵的其余11个未知元素.把这11个未知元素记为11维向量m,则式(11)可以表示如下:
| $ \mathit{\boldsymbol{Km}} = \mathit{\boldsymbol{U}}. $ | (12) |
K和U均为已知量,其中K为2n ×11维矩阵,U为2n维向量.
当提取得到的角点数量满足2n >11时,把已知的棋盘格像素坐标(ui, vi),i = 1~ n和空间坐标(Xwi, Ywi, Zwi),i = 1~ n代入式(12)的K和U中,可以通过最小二乘法求得线性方程的解:
| $ \mathit{\boldsymbol{m}} = {\left( {{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{K}}} \right)^{ - 1}}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{U}}. $ | (13) |
所得的m与m34=1均得到完整的参数矩阵M.
由式(7)可知,所求得参数矩阵M与内外参数关系如下:
| $ {m_{34}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{M}}_1^{\rm{T}}}&{{{\rm{m}}_{14}}}\\ {\mathit{\boldsymbol{M}}_2^{\rm{T}}}&{{{\rm{m}}_{24}}}\\ {\mathit{\boldsymbol{M}}_3^{\rm{T}}}&1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\rm{a}}_0}}&0&{{{\rm{u}}_0}}&0\\ 0&{{{\rm{a}}_{\rm{y}}}}&{{{\rm{v}}_0}}&0\\ 0&0&1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\rm{r}}_1^{\rm{T}}}&{{{\rm{t}}_{\rm{x}}}}\\ {{\rm{r}}_2^{\rm{T}}}&{{{\rm{t}}_{\rm{y}}}}\\ {{\rm{r}}_3^T}&{{{\rm{t}}_{\rm{z}}}}\\ {{{\rm{0}}^T}}&1 \end{array}} \right]. $ | (14) |
其中M1T、M2T、M3T分别为M矩阵第1、2、3列元素的转置.通过式(14)可以求得所有摄像机参数.
2 标定结果及精度分析 2.1 标定参数本次实验所求得完整的参数矩阵M如下:
| $ \begin{array}{l} \mathit{\boldsymbol{M}} = \\ \left[ {\begin{array}{*{20}{c}} {0.0031}&{0.7374}&{ - 0.4204}&{166.2850}\\ {166.29}&{ - 0.0034}&{ - 0.4178}&{163.8553}\\ 0&0&{ - 0.0008}&1 \end{array}} \right] \end{array} $ |
| 表 1 摄像机标定参数 Table 1 Camera calibration internal parameters |
所谓三维重建即通过利用如摄像机等视觉传感器拍摄到的二维图像来估算对应的空间点的三维坐标[13-15].
对静止的物体进行三维重建或在其他静止立体视觉应用场合进行视觉分析时,对于已求出的M矩阵往往不需要对其进行分解,因为M矩阵本身就代表摄像机参数,包含了内外参数信息.本文用棋盘格二维角点图像进行空间三维坐标重建属于上述情况,具体方法如下:
首先,摇动二维手动导轨平台使棋盘格标定板到达允许的测量范围(0~100 mm)内任意一个位置,每隔10 mm拍摄一幅棋盘格图像并记录下该位置的Z坐标值,记为Zr,重复上述步骤连续拍摄11幅棋盘格图像.
然后,对拍摄到的一系列图像提取亚像素角点坐标,记为(ur, vr).
对式(9)和(10)中的Xw、Yw进行显化处理得到如下方程:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{m_{11}} - {u_i}{m_{31}}}&{{m_{12}} - {u_i}{m_{32}}}\\ {{m_{21}} - {v_i}{m_{31}}}&{{m_{22}} - {v_i}{m_{32}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_w}}\\ {{Y_w}} \end{array}} \right] - \\ \left[ {\begin{array}{*{20}{c}} {{u_i}{m_{34}} - {m_{14}} - {Z_{wi}}\left( {{m_{13}} - {u_i}{m_{33}}} \right)}\\ {{v_i}{m_{34}} - {m_{24}} - {Z_{wi}}\left( {{m_{23}} - {v_i}{m_{33}}} \right)} \end{array}} \right] = 0. \end{array} $ | (15) |
记
| $ \left[ {\begin{array}{*{20}{c}} {{X_w}}\\ {{Y_w}} \end{array}} \right] = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{B}}. $ | (16) |
将得到的棋盘格亚像素角点坐标(ur, vr),相应棋盘格标定板所在位置的坐标Zr和已求得的参数矩阵M代入式(17)中,经计算求得11幅任意位置棋盘格图像的所有角点亚像素坐标(ur, vr)对应的三维空间坐标( Xw, Yw, Zr).
2.3 标定精度分析经计算11幅棋盘格图像的所有角点空间三维坐标均已得到.从已得到所有角点空间三维坐标的11幅棋盘格图像的每一幅中任意取一个位置的角点,记录其坐标数据得到表 2.
| 表 2 标定结果数据 Table 2 Calibration result data |
表 2中的角点位置是随机提取,所以具有普遍性.对比表中的3组数据,可以发现角点坐标真实值与经过标定后的计算值之间的误差比较小.
计算11幅棋盘格角点的X坐标和Y坐标真实值与重建计算值的之间的误差,并把位于相同位置的角点坐标误差值相连得到100条误差值曲线,如图 6所示.

|
图 6 误差曲线图 Figure 6 Error curve |
从图 6(a)和图 6(b)中可以看到X方向的误差和Y方向的误差均在-0.05~0.05 mm之间.
最后计算横坐标和纵坐标平均误差:
| $ {X_{{\rm{err}}}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\left( {X - {X_r}} \right)} \right|} ,n = 1\;100. $ | (17) |
| $ {Y_{{\rm{err}}}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\left( {Y - {Y_r}} \right)} \right|} ,n = 1\;100. $ | (18) |
经计算Xerr = 0.021 mm,Yerr = 0.026 mm.可见基于棋盘格标定板结合二维手动导轨平台的单目摄像机标定方法的标定精度足够高,可以满足三维重建的要求.
3 结论本文提出了一种基于棋盘格模板的单目摄像机标定方法,该方法利用高精度CCD摄像机对摆放在二维手动导轨平台上沿Z坐标轴改变固定值的棋盘格标定模板进行多次拍摄,并提取亚像素角点,最后利用DLT标定方法求出所有摄像机参数.在本文最后对该方法的标定精度进行了测试,利用标定好的系统对摆放在二维手动导轨平台上沿Z坐标轴改变任意位置的棋盘格标定模板拍摄并对角点坐标进行三维重建,重建所得横坐标和纵坐标平均误差均能达到±0.02 mm.从实验结果表明基于棋盘格标定模板的单目摄像机高精度标定方法能够快速、有效地获取高精度的摄像机参数矩阵,而且可以很好地满足三维重建及其他视觉检测应用场合的使用要求.
| [1] |
Zhang Z Y. A flexible new technique for camera calibration[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334.
DOI: 10.1109/34.888718. |
| [2] |
Tsai R. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses[J].
IEEE Transactions on Robotics and Automation, 1987, 3(4): 323-344.
DOI: 10.1109/JRA.1987.1087109. |
| [3] |
Heikkila J, Silven O. A four-step camera calibaration procedure with implicit image correction[C]//IEEE Computer Society Conference on Conputer Vision and Pattern Recognition. San Juan: IEEE Press, 1997: 1106-1112.
http://robots.stanford.edu/cs223b04/JeanYvesCalib/papers/heikkila97.pdf
|
| [4] |
梁志敏, 高洪明, 王志江, 等. 摄像机标定中亚像素级角点检测算法[J].
焊接学报, 2006, 27(2): 102-104.
Liang Z M, Gao H M, Wang Z J, et al. Sub-pixels corner detection for camera calibration[J]. Transactions of the China Welding Institution, 2006, 27(2): 102-104. |
| [5] |
刘阳, 王福利, 常玉清, 等. 黑白棋盘格角点检测算法[J].
东北大学学报:自然科学版, 2007, 28(8): 1090-1093.
Liu Y, Wang F L, Chang Y Q, et al. Black and White X-Corner Detection Algorithm[J]. Journal of Northeastern University:Natural Science Edition, 2007, 28(8): 1090-1093. |
| [6] |
罗钧, 王莲, 侯艳. 摄像机标定的棋盘格亚像素角点检测[J].
重庆大学学报, 2008, 31(6): 615-618.
Luo J, Wang L, Hou Y. Sub-pixel corner detection of tessellated picture based on camera calibration[J]. Journal of Chongqing University, 2008, 31(6): 615-618. DOI: 10.11835/j.issn.1000-582X.2008.06.005. |
| [7] |
杨幸芳, 黄美玉, 高峰, 等. 用于摄像机标定的棋盘图像角点检测新算法[J].
仪器仪表学报, 2011, 32(5): 1109-1113.
Yang X F, Huang M Y, Gao F, et al. New corner detection algorithm of chessboard image for camera calibration[J]. China Journal of Scientific Instrument, 2011, 32(5): 1109-1113. |
| [8] |
张裕, 方康玲, 刘永祥. 基于Harris算法的黑白棋盘格角点检测[J].
计算机应用与软件, 2010, 27(8): 251-254.
Zhang Y, Fang K L, Liu Y X. Harris algorithm-based corner detection on black white checkerboard[J]. Computer Applications and Software, 2010, 27(8): 251-254. |
| [9] |
何海清, 黄声亨. 改进的Harris亚像素角点快速定位[J].
中国图像图形学报, 2012, 17(7): 853-857.
He H Q, Huang S H. Improved algorithm for Harris rapid sub-pixel corners detection[J]. Journal of Image and Graphics, 2012, 17(7): 853-857. |
| [10] |
Harris C, Stephens M. A combined corner and edge detector[C]//Proceeding Fourth Alvey Vision Conference. UK, Manchester: [s. n. ]1988: 147-151.
http://www.bmva.org/bmvc/1988/avc-88-023.pdf
|
| [11] |
Ryu J B, Lee C G, Park H H. Formula for Harris corner detector[J].
Electionics Letters, 2011, 47(3): 180-181.
DOI: 10.1049/el.2010.3403. |
| [12] |
Tissainayagam S D. Assessing the performance of corner detectors for point feature tracking applications[J].
Image and Vision Computing, 2004, 22(8): 663-679.
DOI: 10.1016/j.imavis.2004.02.001. |
| [13] |
李立冬, 刘教民. 单目视图下相机标定和平面测距研究[J].
河北科技大学学报, 2005, 26(1): 47-50.
Li L D, Liu J M. Research on camera calibration and plane measurement from a single view[J]. Journal of Hebei University of Science and Technology, 2005, 26(1): 47-50. DOI: 10.7535/hbkd.2005yx01012. |
| [14] |
杨忠根. 基于最小冗余子集的单视图鲁棒精确复原目标三维位姿[J].
模式识别与人工智能, 2001, 14(1): 38-41.
Yang Z G. Robust and accurate pose determination from object's single view based on minimal redundant subset principle[J]. Pattern Recognition and Artificial Intelligence, 2001, 14(1): 38-41. |
| [15] |
张元元, 吴晓娟, 李秀媛, 等. 单目平行线约束下的空间点坐标恢复[J].
智能系统学报, 2010, 5(1): 24-29.
Zhang Y Y, Wu X J, Li X Y, et al. Extraction of 3-D coordinates using parallel lines in monocular images[J]. CAAI Transaction on Intellgent Systems, 2010, 5(1): 24-29. |
 2015, Vol. 32
2015, Vol. 32

