2. 广东工业大学 经济与贸易学院,广东 广州 510520
2. School of Economics and Commerce, Guangdong University of Technology, Guangzhou 510520, China
20世纪90年代以来,R&D全球化趋势逐渐增强,在激烈的市场竞争环境下,企业为保持竞争优势不断进行R&D活动,R&D过程既是技术创新的过程也是供应链的整合过程,供应链企业意识到真正的竞争是供应链与供应链之间的竞争[1].近年来,由于企业R&D活动的重要性使得其受到政府部门的广泛关注,政府对企业的R&D投入反映了一个国家科技实力的重要指标,又是提高国家综合国力和竞争力的重要基础.2011年,我国投入R&D经费8 687亿元,比上年增加1 624.4亿元,同比增长23%,R&D投入强度上升为1.84%[2],但与发达国家相比,现阶段我国企业的R&D投入不足,因此企业的R&D活动仍离不开政府的支持与引导.然而有观点认为,政府资助可能会挤出企业自有R&D投入,同时采取何种资助方式也尚未达成一致意见[3].对于供应链成员间的R&D活动, 政府的参与是否更有利于供应链成员的R&D,国内外学者已经做了许多研究并且证实政府对企业的R&D补贴效果受多重因素的影响[4].因此,有必要对以政府补贴为背景的供应链上成员企业R&D活动进行深入研究.
R&D合作能够分担R&D风险和成本[5],并通过互补和协同效应实现企业能力的提升.然而,由于技术创新本身固有的不确定性和复杂性,R&D的机会主义行为空间较大,管理不当就会产生道德风险,影响R&D绩效.机会主义所导致的“搭便车”现象是R&D的主要原因.因此,如何选择R&D策略,以控制道德风险,是亟待解决的重要问题.通过对R&D方式选择的现有研究进行归纳发现,国内外学者已经对企业的R&D及其影响因素给予了极大的关注.比如文守逊,黄克将网络外部性函数引入D′Aspremont C和Jacquemin A[6]的模型中,研究了双寡头企业的R&D活动,在R&D阶段有合作和竞争两种情况下讨论了网络外部性对企业R&D投入、最优溢出、企业利润和社会福利的影响[7].秦玮等[8]将R&D联盟合作伙伴的行为分为互惠主义行为和机会主义行为,基于演化博弈理论构建了合作伙伴行为选择的演化博弈模型,探讨了吸收能力对R&D联盟合作伙伴行为的影响.侯光明,艾凤义[9]提出了混合溢出的概念,研究在混合溢出下同行业双寡头间的R&D合作,采用博弈论的方法,以AJ模型为基础,对双寡头在R&D上合作与不合作两种情形进行分析.黄波等[10]以AJ模型为基础,建立供应链上下游企业在R&D具有纵向溢出效应时的博弈模型,采用逆向归纳法求出了模型均衡解.D′Aspremont C和Jacquemin A最早采用完全信息动态博弈研究RJV(Research Joint Venture)中R&D合作,作者针对双寡头市场结构下的R&D合作与非合作情况进行分析.Kamien M I等[11]用博弈论分析比较了寡头市场上4种寡头企业的R&D组织模式:R&D有限竞争、R&D卡特尔、RJV竞争和RJV卡特尔.Larry D等[12]在产业经济学和战略贸易理论的框架下,分析了有关政府R&D博弈活动的基本特征,讨论了企业间R&D国际活动中政府的最优政策设计问题,分析了政府R&D补贴及关税的竞争优势和刺激效应,得到了政府补贴政策和企业R&D合作模式正相关的结论.Chan等[13]结合R&D与营销策略研究了供应链上绩效评价体系的问题.Ge Z等[14]研究了供应链上两家企业的R&D合作行为,两家企业在R&D投入方面进行合作,然后根据批发价格合同来决定产量,通过产出水平来衡量供应链上企业在R&D合作方面的技术贡献,只有当两家企业的贡献水平是帕累托最优,两家企业通过组成卡特尔才能达到双赢的状态.Rokuhara等[15]对日本公司研发合作的研究表明,近90%的公司之间的研发合作主要是是供应链纵向的上、下游企业的R&D合作.可以看出纵向R&D合作方式在加工业中是非常重要的R&D合作方式,因此对供应链上下游企业的R&D策略的研究十分有必要.
现有研究为企业的R&D模式的选择提供了重要依据,但这些研究并没有考虑供应链中R&D因素以及企业自身与供应链其他成员企业理性程度因素的影响.此前大多供应链上下游企业的R&D演化博弈模型[16]都是建立在两群体的理论基础之上.然而,由于供应链结构的复杂性及外部因素影响,仅仅考虑两个群体是不能反映供应链的整体效益的.因此,本文的研究与上述研究比较有如下特点:首先,本文的研究对象是供应链上的上下游企业的R&D策略的选择,且考虑了政府的补贴行为.其次,过去对供应链R&D的研究,大都是建立在供应链成员企业理性假设的基础之上,但现实供应链节点企业不可能是完全理性的.因此,利用有限理性[17]为基础的演化博弈论来研究供应链上下游企业间R&D竞争与合作策略的选择将更符合实际情况.
1 研究假设与模型分析本节首先对供应链企业间研发(R&D)的演化过程进行研究,即针对供应链上供应商和制造商在研发竞争与研发合作过程中受政府补贴影响的行为建立三方的演化博弈模型,分析供应链中成员间R&D的演化路径及其影响因素.
1.1 模型假设假设1 该供应链由供应商、制造商两家企业组成并进行R&D活动,政府作为第三方对供应链上、下游进行R&D活动的企业给予相应的补贴.
假设2 制造商选择R&D合作策略的概率为x,选择R&D竞争策略的概率为1-x,供应商选择R&D合作策略的概率为y,选择R&D竞争策略的概率为1-y,政府对于制造商与供应商选择补贴策略的概率为z,选择不补贴策略的概率为1-z. x,y,z∈[0, 1].
假设3 制造商、供应商都选择R&D合作策略时政府给予的补贴表示为B,若双方选择不同策略时,政府给予选择R&D合作策略的一方补贴表示为B′;制造商、供应商R&D投入的成本分别为C1,C2,制造商与供应商都选择R&D合作策略时的额外收益分别为e1,e2;制造商与供应商选择R&D时的基本收益分别为w1,w2;政府在制造商与供应商都选择R&D合作策略时获得的收益为w,若只有一方选择R&D合作策略时政府的收益则为w′.
参与者根据博弈方的策略、收益以及自身的情况进行比较,在有限理性的状态下模仿和学习的过程中不断调整自己的策略.下面给出三方博弈的支付矩阵如表 1所示
| 表 1 政府、供应商及制造商的博弈支付矩阵 Table 1 Payoff structure of the game with the government, supplier and manufacturer |
制造商选择R&D合作策略的期望收益Ux, 选择R&D竞争策略的期望收益U1-x,平均期望收益U1, 分别为
| $ \begin{array}{l} {U_x} = \left[{\left( {{w_1} + {e_1}-{C_1} + B} \right)y + \left( {{w_1}-{C_1} + B\prime } \right)\left( {1-y} \right)} \right]\\ z + \left[{\left( {{w_1} + {e_1}-{C_1}} \right)y + \left( {{w_1}-{C_1}} \right)\left( {1-y} \right)} \right]\left( {1 -z} \right), \end{array} $ |
| $ \begin{array}{l} {U_{1- x}} = \left[{\left( {{w_1}-{C_1}} \right)y + \left( {{w_1}-{C_1}} \right)\left( {1-y} \right)} \right]\\ z + \left[{\left( {{w_1}-{C_1}} \right)y + {w_1}\left( {1-y} \right)} \right]\left( {1 -z} \right), \end{array} $ |
| $ {{\bar U}_1} = x{U_x} + \left( {1-x} \right){U_{1-x}}. $ |
制造商演化博弈的动态复制方程为
| $ \begin{array}{l} \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = \dot x = x({U_x}- \mathit{\bar U}{_1}) = x\left( {1- x} \right)\\ \left[{\left( {1-y} \right)\left( {B\prime z-{\rm{ }}{C_1} + {C_1}z} \right) + y\left( {Bz + {e_1}} \right)} \right], \end{array} $ | (1) |
其中
同理,供应商选择R&D合作策略的期望收益Uy,选择R&D竞争策略的期望收益U1-y,平均期望收益U2, 分别为
| $ \begin{array}{l} {U_y} = \left[{\left( {{w_2} + {e_2}-{C_2} + B} \right)x + \left( {{w_2}-{C_2} + B\prime } \right)\left( {1-{\rm{ }}x} \right)} \right]z + \\ \left[{\left( {{w_2} + {e_2}-{C_2}} \right)x + \left( {{w_2}-{C_2}} \right)\left( {1-x} \right)} \right]\left( {1 -z} \right), {\rm{ }} \end{array} $ |
| $ \begin{array}{l} {U_{1-y}} = \left[{\left( {{w_2}-{C_2}} \right)x + \left( {{w_2}-{C_2}} \right)\left( {1-x} \right)} \right]z + \\ \left[{\left( {{w_2}-{C_2}} \right)x + {w_2}\left( {1-x} \right)} \right]\left( {1 -z} \right), \end{array} $ |
| $ {{\mathit{\bar U}}_2} = y{U_y} + \left( {1-y} \right){U_{1-y}}. $ |
供应商演化博弈的动态复制方程为
| $ \begin{array}{l} \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = \dot y = y({U_y}- {{\mathit{\bar U}}_2}) = y\left( {1- y} \right)\\ \left[{\left( {1-{\rm{ }}x} \right)\left( {B\prime z-{C_2}} \right) + x\left( {{C_2}z + Bz + {e_2}} \right) + {C_2}z} \right]. \end{array} $ | (2) |
类似地,政府采取补贴策略的期望收益Uz,选择不补贴策略的期望收益U1-z,平均期望收益U3, 分别为
| $ \begin{array}{l} {U_z} = \left[{\left( {w-2B} \right)y + \left( {w\prime-B\prime } \right)\left( {1-y} \right)} \right]x + \\ \left( {w\prime -{\rm{ }}B\prime } \right)y\left( {1 -x} \right), \end{array} $ |
| $ \begin{array}{l} {U_{1- z}} = \left[{wy + w\prime \left( {1-y} \right)} \right]x + \\ w\prime y(1 -x), \end{array} $ |
| $ {{\mathit{\bar U}}_3} = z{U_z} + \left( {1-z} \right){U_{1-z}}. $ |
政府演化博弈的动态复制方程为
| $ \begin{array}{l} \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = \dot z = z({U_z}- {{\mathit{\bar U}}_3}) = z\left( {1- z} \right)\\ \left[{2\left( {B\prime-B} \right)xy-B\prime x-B\prime y} \right]. \end{array} $ | (3) |
由式(1)~(3)构成了一个动态复制系统.在动态的博弈过程中,博弈三方选取策略的概率x、y、z与时刻t有关,因而可表示成x(t)、y (t)、z (t)∈[0, 1],由此可知由式(1)~(3)构成的动态复制系统的解域为[0, 1]×[0, 1]×[0, 1].
为寻求演化博弈的均衡点,对于上述动态复制系统只要讨论
系统的均衡点稳定性,可由Jacobian矩阵局部分析法判断.根据上述制造商、供应商及政府的成本收益情况,下面分别对制造商、供应商及政府三方的策略相互影响的动态演化过程进行分析.该系统的雅克比矩阵为
| $ \mathit{\boldsymbol{J = }}\left( {\begin{array}{*{20}{c}} {\frac{{\partial \dot x}}{{\partial x}}}&{\frac{{\partial \dot x}}{{\partial y}}}&{\frac{{\partial \dot x}}{{\partial z}}}\\ {\frac{{\partial \dot y}}{{\partial x}}}&{\frac{{\partial \dot y}}{{\partial y}}}&{\frac{{\partial \dot y}}{{\partial z}}}\\ {\frac{{\partial \dot z}}{{\partial x}}}&{\frac{{\partial \dot z}}{{\partial y}}}&{\frac{{\partial \dot z}}{{\partial z}}} \end{array}} \right). $ |
动态复制系统在平衡点E1=(0, 0, 0)处的雅克比矩阵为
| $ \mathit{\boldsymbol{J = }}\left( {\begin{array}{*{20}{c}} {-{C_1}}&0&0\\ 0&{-{C_2}}&0\\ 0&0&0 \end{array}} \right). $ |
矩阵J的特征值为:λ 1 = - C1,λ 2 = - C2,λ3= 0.由李雅普诺夫第一法知平衡点E1 (0, 0, 0)不是稳定点.按照同样的方法对其他均衡点进行稳定性分析,结果如表 2所示.
| 表 2 各均衡点的稳定性判断 Table 2 The estimated stability of every equilibrium point |
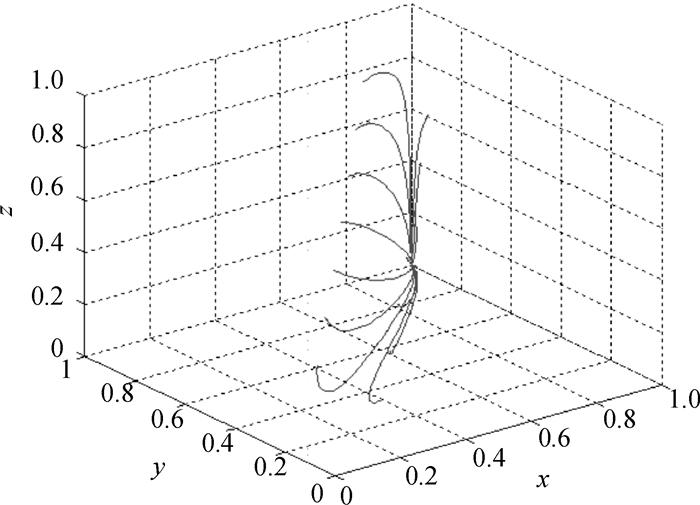
为了验证上述判断,通过Matlab软件进行数值模拟仿真分析,进一步证实给出不同初始值后不同平衡点的演化轨迹.考虑到模型中各参数均大于等于0,取B ′=10,B =5,C1=4,C2=2,e1=12,e2=9,代入相应的条件式中,并根据条件设定不同的初始值,仿真图中3条坐标轴分别表示x,y和z,即制造商选择R&D合作策略的比例,供应商选择R&D合作策略的比例,政府选择补贴策略的比例.在[0, 1]×[0, 1]×[0, 1]空间中得到供应链上下游企业及政府三方博弈的动态演化图如图 1所示.
|
图 1 制造商、供应商及政府三方博弈的动态演化图 Figure 1 The dynamic evolution of three-party game |
由图 1可知E1(0, 0, 0)、E2(1, 0, 0)、E3(0, 1, 0)、E4(0, 0, 1)、E6(1, 0, 1)、E7(0, 1, 1)、E8(1, 1, 1)都是不稳定点,而且都是鞍点,只有E5(1, 1, 0)是该博弈系统的演化稳定点,此时的E5(1, 1, 0)是该博弈的严格纳什均衡,即制造商与供应商都选择R&D合作策略,政府选择不补贴.
2 结论与建议本文基于理论分析,从演化博弈的角度,采用动态复制方程,建立了供应链上下游企业及政府为主体的三方博弈模型,并对此进行演化博弈稳定性分析,得到各方合理的选择策略.研究表明,在制造商、供应商及政府三方博弈中,各方所选策略的稳定性除了取决于自身成本收益影响以外还受其他博弈方的相关支付因素影响;在三方博弈模型中,从互惠主义行为考虑,供应链上下游企业最终会采取R&D合作策略,政府选择不补贴策略,这也是政府期望的系统演化方向,进一步证实了供应链上下游企业的R&D合作也是一种共赢的策略.针对上述分析,给出如下建议.
首先,针对供应链上成员企业间的利益分配与成本分担制定合理的机制.在供应商与制造商参与的供应链R&D活动过程中,制造商与供应商的收益分配直接影响到双方R&D合作的积极性,供应链中供应商的R&D有利于降低生产成本,同时也可以使下游的制造商以较低的采购价格获得产品并从中获得一定增量的利润.因此,合理的收益分配与成本分担机制是影响供应链上下游企业R&D合作的重要因素.
其次,为了尽量避免供应链R&D合作的双方出现机会主义行为,政府要明确奖惩制度.由于R&D合作是供应链上下游企业与政府在技术创新方面实现双赢的科学途径,供应链上的成员企业期望通过R&D合作分担研发成本,分散风险,实现供应链上企业间的资源共享和能力互补,政府则期望通过R&D合作提高企业技术水平、经济效益与促进国民经济增长的良性发展.因此,有效的监督和明确的奖惩机制,有利于减少双方的机会主义收益.
本文在模型建立过程中没有考虑企业的吸收能力和技术溢出效应,现实情况中一般R&D活动会存在技术溢出、吸收能力等因素[18]的影响,这将是本文进一步研究的方向.
| [1] |
刘金芳, 徐枞巍, 高波. 供应链整合创新的演化博弈分析[J].
系统工程, 2011, 29(8): 8-13.
Liu J F, Xu Z W, Gao B. Evolutionary game analysis of supply chain integration and innovation[J]. Systems Engineering, 2011, 29(8): 8-13. |
| [2] |
于泊, 陈岩. 我国R&D活动的现状[J].
中国外资, 2014(2): 239-239.
Yu P, Chen Y. The current situation of R&D activities in China[J]. Foreign Investment in China, 2014(2): 239-239. |
| [3] |
Goolsbee A. Does government R&D policy mainly benefit scientists and engineers[J].
American Economic Review, 1998, 88(2): 298-302.
|
| [4] |
段蕊蕊, 代明, 刘佳. 我国政府R&D资助的效果测度——基于工业行业视角[J].
西安经济学院学报, 2014, 27(1): 29-34.
Duan R R, Dai M, Liu J. The effect measurement of fiscal R&D subsidies in China-based on industries' perspective[J]. Journal of Xi'an University of Finance and Economics, 2014, 27(1): 29-34. |
| [5] |
汪翔, 孟卫东, 吴国东. 不确定性条件下研发联盟的风险分担设计[J].
管理工程学报, 2013, 27(3): 189-195.
Wang X, Meng W D, Wu G D. Design on risk sharing of R&D alliance on the condition of uncertainty[J]. Journal of Industrial Engineering Management, 2013, 27(3): 189-195. |
| [6] |
D'Aspremont C. Cooperative and noncooperative R&D in duopoly with spillovers[J].
American Economic Review, 1988, 78: 1133-1137.
|
| [7] |
文守逊, 黄克. 网络外部性下的企业R&D竞争与合作行为研究[J].
中国管理科学, 2008, 15(z1): 578-581.
Wen S X, Huang K. The study on firm's R&D noncooperation and cooperation with network externalities[J]. Chinese Journal of Management Science, 2008, 15(z1): 578-581. |
| [8] |
秦玮, 徐飞, 宋波. 研发联盟合作伙伴行为演化博弈分析——吸收能力的视角[J].
工业工程与管理, 2012, 16(6): 16-20.
Qin W, Xu F, Song B. Evolutionary game analysis of behavior in R&D alliances with absorptive capacity perspective[J]. Industrial Engineering and Management, 2012, 16(6): 16-20. |
| [9] |
侯光明, 艾凤义. 基于混合溢出的双寡头横向R&D合作[J].
管理工程学报, 2006, 20(4): 94-97.
Hou G M, Ai F Y. Horizontal R&D cooperation of a duopoly based on mixed spillovers[J]. Journal of Industrial Engineering Management, 2006, 20(4): 94-97. |
| [10] |
黄波, 孟卫东. 基于双向溢出效应的供应链合作研发博弈模型[J].
科技管理研究, 2009(3): 177-179.
Huang B, Meng W D. Cooperative R&D game model with spillover effect in supply chain[J]. Science and Technology Management Research, 2009(3): 177-179. |
| [11] |
Kamien M I, Muller E, Zang I. Research joint ventures and R&D cartels[J].
The American Economic Review, 1992, 82(5): 1293-1306.
|
| [12] |
Qiu L D, Tao Z G. Policy on international R&D cooperation: Subsidy or tax[J].
European Economic Review, 1998, 42(9): 1727-1750.
DOI: 10.1016/S0014-2921(97)00097-4. |
| [13] |
Chan F T S, Nayak A, Raj R, et al. An innovative supply chain performance measurement system incorporating research and development (R&D) and marketing policy[J].
Computers & Industrial Engineering, 2014, 69: 64-70.
|
| [14] |
Ge Z, Hu Q, Xia Y. Firms' R&D cooperation behavior in a supply chain[J].
Production and Operations Management, 2013, 23(4): 599-609.
|
| [15] |
Banerjee S, Lin P. Vertical rsearch joint ventures[J].
International Journal of Industrial Organization, 2001(19): 285-302.
|
| [16] |
黄敏镁. 基于演化博弈的供应链协同产品开发合作机制研究[J].
中国管理科学, 2010, 18(6): 155-162.
Huang M M. Evolutionary game analysis of cooperation mechanism for collaborative Product development in supply chain[J]. Chinese Journal of Management Science, 2010, 18(6): 155-162. |
| [17] |
杨建飞. 寡头垄断企业R&D博弈模式及其政策选择的思想演变与前沿倾向[J].
宝鸡文理学院学报, 2013, 33(4): 20-25.
Yang J F. The game pattern as well as ideological evolution and research tendency of oligopolistic enterprise R&D[J]. Journal of Baoji University of Arts and Science, 2013, 33(4): 20-25. |
| [18] |
张春辉. 基于动态能力与研发因素视角的创新模式选择研究[D]. 上海: 上海交通大学管理学院, 2012.
|
 2015, Vol. 32
2015, Vol. 32