2. 广东工业大学 信息工程学院, 广东 广州 510006;
3. 西安邮电大学 自动化学院,陕西 西安 710121
2. School of Information Engineering, Guangdong University of Technology, Guangzhou 510006, China;
3. School of Automation, Xi'an University of Posts and Telecommunications, Xi'an 710121, China
在工程实践与应用中,由于组件众多、结构复杂和元器件性能为非线性等原因,某些工程系统容易产生不规则和不可预测的混沌行为,这些混沌行为可能会危害系统正常运转[1].因此,几十年来,混沌系统的镇定吸引了科学与工程界的关注, 其中通过状态反馈控制法镇定混沌系统是研究的一个重要方面[2-8].然而,这些研究成果中,需要混沌系统的连续时间状态测量值,即连续的测量状态值直接传递给反馈控制器.实际上,随着计算机控制技术的发展,用作控制器输入信号的系统状态通常需要用一些额外的信息处理设备如传感器、编码器和传输设备等进行检测和传输.文献[9]提到,因为硬件设备总会导入某种形式的不精确性,系统状态不可能精确测定.当利用数字装置时,产生测量误差的一个重要原因是由于只能获取状态的量化值,即控制器的输入信号实际上只能是状态的有限个量化数值[10].随着计算机数字控制技术的普及,由于数字控制过程A/D和D/A转换器的作用,数字控制器和混沌系统必将交互作用互相影响.由于数模转换器比特位数是有限的,混沌系统的真实状态变量的有限字长表达或量化效应显示为有效带宽通信信道,因而数字状态反馈控制器可能导致非预定的镇定控制结果.例如,量化可导致极限环或者混沌行为,也可导致数字反馈系统的不稳定性[11-12].文献[12]研究了有DSP芯片系统的状态与输入信号量化的效应,结果表明,一些连续系统,若取比较高的采样频率,系统对量化系数不确定性较敏感,这更易导致系统不稳定.混沌系统是一种特殊的非线性系统,对初始状态极端敏感.因此混沌系统的状态量化更可能导致不稳定.所以有必要对状态量化反馈控制的混沌系统的镇定方法加以研究.
过去几十年中,文献[13-15]应用静态量化方法镇定线性系统.文献[16-19]在设计非线性系统的反馈镇定控制器时,分析了时变量化方法,结果表明时变量化法比静态量化法能更好地镇定系统.从数学模型的角度看,混沌系统的模型拥有特殊的结构, 并对参数极其敏感,这暗示状态量化过程可能导致系统结构的变化并弱化反馈控制器的效率.基于以上思路,文献[20]率先将一种时变自适应量化方法用于控制一类混沌系统,可镇定非线性项为二次齐次函数的混沌系统.这是一种数学前提条件比较严格的方法,普适性比较差.本文将在其基础上进行拓展,提高量化状态反馈镇定法的适用范围,使之可以自适应镇定非线性项为高次齐次函数的一大类混沌系统.
1 带有高次齐次函数的混沌系统考虑如下混沌动态系统
| $ \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + F\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{C}}. $ | (1) |
其中系统的状态矢量为x =(x1, x2, …, xn)T,x ∈ Rn,n为系统状态维数,A =(aij)n×n为实数矩阵,F(x)=(f1(x), f2(x), …, fn(x))T为系统非线性项,C =(c1, c2, …, cn)T∈ Rn为常数项.
假定1 对于系统(1),假设
| $ \left| {{f_i}\left( \mathit{\boldsymbol{x}} \right)} \right| \le {\alpha _i}{\left\| \mathit{\boldsymbol{x}} \right\|^m}, $ | (2) |
其中αi>0,‖*‖为欧氏范数,m为正整数.
注1:假定1涵盖了一类具有高次非线性项的混沌系统,例如文献[21-24]所提出的混沌系统,其非线性项呈现为乘积形式:kxixj2、kxixjxl、kxixjxlxm、kxixjxlxmxn等,利用不等式|fi(x)|=|kxkxlxm|=|k|
利用文献[16, 18]的结果, 本文将量化器定义为q:Rl→L, z→q(z),其中L为空间Rl的一个有限子集,z∈ Rl为被量化的变量,通过z的量化,Rl被分割为{z ∈ Rl:q(z)=i}(i∈L).量化器满足下面两个条件:
| $ \left\| {q\left( \mathit{\boldsymbol{z}} \right) - \mathit{\boldsymbol{z}}} \right\| < \varepsilon ,当\;\left\| \mathit{\boldsymbol{z}} \right\| \le M\;时, $ | (3a) |
| $ \left\| {q\left( \mathit{\boldsymbol{z}} \right)} \right\| > M - \varepsilon ,当\;\left\| \mathit{\boldsymbol{z}} \right\| > M\;时. $ | (3b) |
其中M为量化范围界.式(3a)给出了量化器不饱和时量化误差的界ε,而式(3b)给出了检测量化器饱和的条件.一个典型的量化器公式为
| $ q\left( y \right) = \left\{ \begin{array}{l} M,当\;y > \left( {M + 0.5} \right)\varepsilon ;\\ - M,当\;y \le \left( {M + 0.5} \right)\varepsilon ;\\ \left[ {\frac{y}{\varepsilon } + 0.5} \right],其他. \end{array} \right. $ | (4) |
其中函数[y]为四舍五入取整函数.
受文献[16, 18-19]的启发,可以将一个时变参数β=β(t)引入到量化器(3)中,形成带有时变参数的量化器, 其量化的结果为
| $ Q = \beta q\left( {\frac{\mathit{\boldsymbol{x}}}{\beta }} \right). $ | (5) |
显然当‖x‖≤|β|M时,
现在考虑满足假定1的混沌系统(1), 将控制器u引入到其中形成如下混沌控制系统:
| $ \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + F\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{C}} + \mathit{\boldsymbol{u}}. $ | (6) |
若不考虑系统状态被量化的情况,则可选择非线性控制器为u = Kx -F(x)- C,此时闭环系统为
| $ \mathit{\boldsymbol{X}}{\mathit{\boldsymbol{A}}^{\rm{T}}} + \mathit{\boldsymbol{AX}} + {\mathit{\boldsymbol{Y}}^{\rm{T}}} + \mathit{\boldsymbol{Y}} < 0, $ | (7) |
其中 X >0,且 K = YX -1
但是,如果系统状态被量化,则输入控制器的系统状态不再是 x 而是 q (x),上述非线性控制器改变为
| $ \mathit{\boldsymbol{u}} = \mathit{\boldsymbol{Kq}}\left( \mathit{\boldsymbol{x}} \right) - F\left( {\mathit{\boldsymbol{q}}\left( \mathit{\boldsymbol{x}} \right)) - \mathit{\boldsymbol{C}}} \right. $ | (8) |
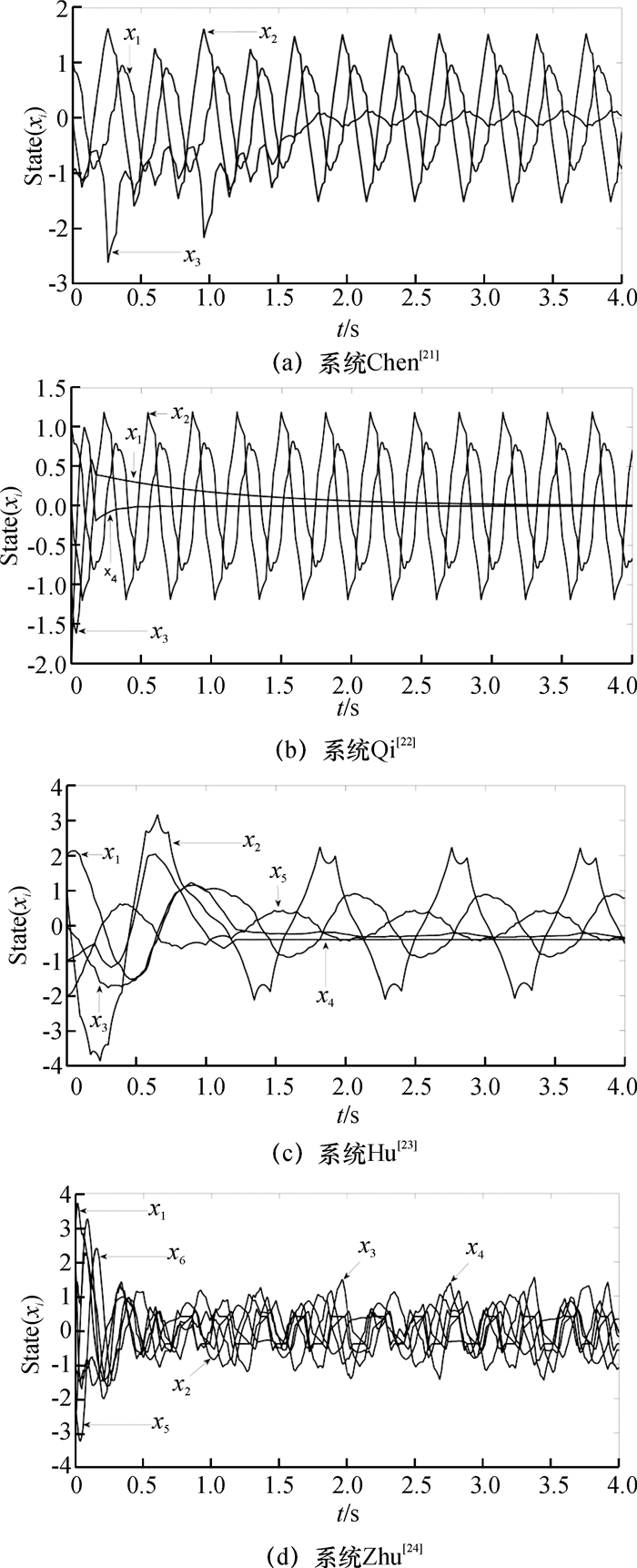
本文的仿真结果表明此非线性控制器将导致混沌控制系统(6)失稳,结果如图 1所示.因此, 有必要考虑系统状态被量化的情形下控制器设计问题.
|
图 1 非线性控制器(8)反馈镇定各混沌系统的数值仿真图 Figure 1 Numerical simulation of stabilization for chaosvia the nonlinear controller (8) |
假定2 针对混沌系统(1), A+K为Hurwitz矩阵.
在系统状态被量化的情形下,本文提出带有形如(5)量化器的控制律:
| $ \begin{array}{l} \mathit{\boldsymbol{u}} = \mathit{\boldsymbol{K}}\left( {\beta q\left( {\frac{\mathit{\boldsymbol{x}}}{\beta }} \right)} \right) - F\left( {\beta q\left( {\frac{\mathit{\boldsymbol{x}}}{\beta }} \right)} \right) - \mathit{\boldsymbol{C}},\\ 当\;\left\| \mathit{\boldsymbol{x}} \right\| \le \left| \beta \right|\mathit{\boldsymbol{M}}\;时; \end{array} $ | (9a) |
| $ \mathit{\boldsymbol{u}} = - \mathit{\boldsymbol{C}},当\;\left\| \mathit{\boldsymbol{x}} \right\| > \left| \beta \right|M\;时. $ | (9b) |
其中, K 由线性矩阵不等式(7)确定, 正定矩阵 P 通过解下列Lyapunov方程(10)获得.
| $ {\left( {\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{K}}} \right)^{\rm{T}}}\mathit{\boldsymbol{P}} + \mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{K}}} \right) = - \mathit{\boldsymbol{Q}}. $ | (10) |
其中 Q 为任意给定的正定矩阵.
在控制器(9)中, 量化器参数β(t)的更新律为
| $ \begin{array}{l} \dot \beta \left( t \right) = \frac{1}{{2\beta {M^2}}}\left[ {\delta + {\lambda _{\max }}\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{ + A}}} \right)\left\| \mathit{\boldsymbol{x}} \right\|_2^2 + } \right.\\ \left. {2\sqrt n \mathop {\max }\limits_{1 \le i \le n} \left( {{\alpha _i}} \right)\left\| \mathit{\boldsymbol{x}} \right\|_2^{m + 1}} \right],当\;\left\| \mathit{\boldsymbol{x}} \right\| > \left| \beta \right|M\;时; \end{array} $ | (11a) |
| $ \begin{array}{l} \dot \beta \left( t \right) = - 2{\lambda _1}M{\lambda _{\max }}\left( \mathit{\boldsymbol{P}} \right)\sqrt n \left[ {\mathop {\max }\limits_{1 \le i \le n} \left( {{\alpha _i}} \right){{\left| \beta \right|}^m}{M^m} + } \right.\\ \left. {\left\| {\beta q\left( {\frac{\mathit{\boldsymbol{x}}}{\beta }} \right)} \right\|_2^m} \right]{\rm{sign}}\left( \beta \right) + \beta \left\| \mathit{\boldsymbol{K}} \right\|\hat \varepsilon ,当\;\left\| \mathit{\boldsymbol{x}} \right\| \le \\ \left| \beta \right|M\;时. \end{array} $ | (11b) |
其中任意实数δ>0,λ1>0.假定量化器的量化误差上界为ε,在工程实践中,一般很难获得精确的误差界.取其估计值为
| $ \dot {\hat \varepsilon} = 2{\lambda _2}\left| \beta \right|M{\lambda _{\max }}\left( \mathit{\boldsymbol{P}} \right)\sqrt n \left\| \mathit{\boldsymbol{K}} \right\|,当\left\| \mathit{\boldsymbol{x}} \right\| \le \left| \beta \right|M\;时; $ | (12a) |
| $ \dot {\hat \varepsilon} = 0,当\left\| \mathit{\boldsymbol{x}} \right\| > \left| \beta \right|M\;时. $ | (12b) |
其中任意实数λ2>0.
定理1 考虑混沌控制系统(6).如果假定1和2成立, 那么控制器(9)、参数更新律(11)和自适应律(12)能够保证混沌控制系统(6)渐近稳定.
证明 (1)当‖x‖>|β|M时,由fi(x) ≤αi‖x‖2m可得
| $ \begin{array}{l} \left\| {F\left( \mathit{\boldsymbol{x}} \right)} \right\| \le \sqrt {f_1^2\left( \mathit{\boldsymbol{x}} \right) + f_2^2\left( \mathit{\boldsymbol{x}} \right) + \cdots + f_n^2\left( \mathit{\boldsymbol{x}} \right)} = \\ \sqrt n \mathop {\max \left( {{\alpha _i}} \right)}\limits_{1 \le i \le n} {\left\| \mathit{\boldsymbol{x}} \right\|^m}. \end{array} $ | (13) |
考虑由混沌系统(6)、参数更新律(11)和自适应律(12)构成的闭环系统,其状态向量为z =(xT, β,
情形1.‖x‖>|β|M
在这种情形下证明在控制器(9)、参数更新律(11)和自适应律(12)的作用下状态z =(xT, β,
| $ \begin{array}{l} \dot V\left( t \right) = s\left( {{{\mathit{\boldsymbol{\dot x}}}^{\rm{T}}}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{\dot x}} - 2\beta {M^2}\dot \beta + \tilde \varepsilon \dot {\tilde \varepsilon} } \right) = \\ s\left( {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}} + \mathit{\boldsymbol{A}}} \right)\mathit{\boldsymbol{x}} + 2{F^{\rm{T}}}\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{x}} - 2\beta {M^2}\dot \beta } \right) \le \\ s\left( {{\lambda _{\max }}\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}} + A} \right){{\left\| \mathit{\boldsymbol{x}} \right\|}^2} + 2\left\| {F\left( \mathit{\boldsymbol{x}} \right)} \right\|\left\| \mathit{\boldsymbol{x}} \right\| - } \right.\\ \left. {2\beta {M^2}\dot \beta } \right) \le s\left( {{\lambda _{\max }}\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}} + \mathit{\boldsymbol{A}}} \right){{\left\| \mathit{\boldsymbol{x}} \right\|}^2} + } \right.\\ \left. {2\sqrt n \mathop {\max \left( {{\alpha _i}} \right)}\limits_{1 \le i \le n} {{\left\| \mathit{\boldsymbol{x}} \right\|}^{m + 1}} - 2\beta {M^2}\dot \beta } \right) = - \delta s. \end{array} $ | (14) |
由式(14)和文献[25]的结论,显然闭环系统的状态z可在有限时间内进入滑模面s=0.注意到{|z|s=0}
情形2. ‖x‖≤|β|M
当‖x‖≤|β|M时,由量化器条件(3a)可得:
| $ \begin{array}{l} \left\| {\frac{\mathit{\boldsymbol{x}}}{\beta } - q\left( {\frac{\mathit{\boldsymbol{x}}}{\beta }} \right)} \right\| = \left\| {\left( {\frac{{{x_1}}}{\beta } - q\left( {\frac{{{x_1}}}{\beta }} \right),\frac{{{x_2}}}{\beta } - q\left( {\frac{{{x_2}}}{\beta }} \right),} \right.} \right.\\ \left. { \cdots ,{{\left. {\frac{{{x_n}}}{\beta } - q\left( {\frac{{{x_n}}}{\beta }} \right)} \right)}^{\rm{T}}}} \right\| \le \sqrt n \varepsilon . \end{array} $ | (15) |
由假定(1)可推导出:
| $ \begin{array}{l} \left\| {F\left( \mathit{\boldsymbol{x}} \right) - F\left( {\beta q\left( {\frac{\mathit{\boldsymbol{x}}}{\beta }} \right)} \right)} \right\| \le \sqrt n \mathop {\max \left( {{\alpha _i}} \right)}\limits_{1 \le i \le n} \left( {{{\left\| \mathit{\boldsymbol{x}} \right\|}^m} + } \right.\\ \left. {{{\left| \beta \right|}^m}{{\left\| {q\left( {\frac{\mathit{\boldsymbol{x}}}{\beta }} \right)} \right\|}^m}} \right). \end{array} $ | (16) |
对正定函数V(x)=V(xT, β,
| $ \begin{array}{l} \dot V\left( t \right) = 2{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{P\dot x}} + \lambda _1^{ - 1}\beta \dot \beta + \lambda _2^{ - 1}\tilde \varepsilon \dot {\tilde \varepsilon} = \\ 2{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{Ax}} + F\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{K}}\left( {\beta q\left( {\frac{\mathit{\boldsymbol{x}}}{\beta }} \right)} \right) - F\left( {\beta q\left( {\frac{\mathit{\boldsymbol{x}}}{\beta }} \right)} \right) - } \right.\\ \left. {\mathit{\boldsymbol{C}} + \mathit{\boldsymbol{Kx}} - \mathit{\boldsymbol{C}}} \right) + \lambda _1^{ - 1}\beta \dot \beta + \lambda _2^{ - 1}\tilde \varepsilon \dot {\tilde \varepsilon} = \\ 2{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{K}}} \right)\mathit{\boldsymbol{x}} + 2{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {F\left( \mathit{\boldsymbol{x}} \right) - F\left( {\beta q\left( {\frac{\mathit{\boldsymbol{x}}}{\beta }} \right)} \right)} \right) - \\ 2{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{P}}\beta \mathit{\boldsymbol{K}}\left( {\frac{\mathit{\boldsymbol{x}}}{\beta } - q\left( {\frac{\mathit{\boldsymbol{x}}}{\beta }} \right)} \right) + \lambda _1^{ - 1}\beta \dot \beta + \lambda _2^{ - 1}\tilde \varepsilon \dot {\tilde \varepsilon} \le \\ - {\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{Qx}} + 2\left\| \mathit{\boldsymbol{x}} \right\|{\lambda _{\max }}\left( \mathit{\boldsymbol{P}} \right)\sqrt n \mathop {\max \left( {{\alpha _i}} \right)}\limits_{1 \le i \le n} \left( {{{\left\| \mathit{\boldsymbol{x}} \right\|}^m} + } \right.\\ \left. {{{\left| \beta \right|}^m}{{\left\| {q\left( {\frac{\mathit{\boldsymbol{x}}}{\beta }} \right)} \right\|}^m}} \right) + 2\left\| \mathit{\boldsymbol{x}} \right\|{\lambda _{\max }}\left( \mathit{\boldsymbol{P}} \right)\left| \beta \right|\left\| \mathit{\boldsymbol{K}} \right\|\sqrt n \varepsilon + \\ \lambda _1^{ - 1}\beta \dot \beta + \lambda _2^{ - 1}\tilde \varepsilon \dot {\tilde \varepsilon} = - {\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{Qx}} \end{array} $ | (17) |
不等式(17)表明,闭环控制系统的状态z有界, 即状态 x 有界.由式(1),(3),(5)和(6)可知,β、
本文从文献[21-24]中选择4个典型的混沌系统进行数值仿真.这4个系统的系统状态维数依次为3到6维,系统非线性项分别含2到5次齐次函数,混沌系统的具体参数如表 1所示,其中K为混沌控制系统的增益矩阵,x0为混沌控制系统的初始状态,常数项C都为0.
| 表 1 4个用于数值仿真混沌系统的参数表 Table 1 The parameters of four chaotic systems for numerical simulation |
首先用非线性控制器(8)对表 1的4个典型混沌系统进行反馈镇定,其中系统状态是被静态均匀量化器(4)量化,数值仿真结果依次如下图 1的(a)至(d)所示.
图 1的仿真结果表明,非线性控制器(8)无法反馈镇定混沌控制系统(6).
是否可以使用文献[19]中的方法反馈镇定上述一类混沌系统?文献[19]的核心思想是找出混沌系统所有非线性项的Hessian矩阵的最大特征值,用于更新非线性控制器(9)中量化器的时变参数.为此,必须假定所有Hessian矩阵为常数矩阵,从而混沌系统的非线性项必须为2次以下齐次函数,即文献[19]适用范围仅为非线性项为2次以下齐次函数.而文献[21-24]中混沌系统的非线性项都含有3次以上的高次齐次函数,所得Hessian矩阵必然为时变矩阵,无法确定最大的特征值,从而无法使用文献[19]方法进行数值仿真.因此, 必须重新设计非线性控制器.
针对上述一类混沌系统,按照本文方法设计时变非线性控制器(9),其中自适应量化器的参数变化规律为(11)和(12),并取量化器放大系数初始值β(0)=0.1和量化误差估计值初始值
|
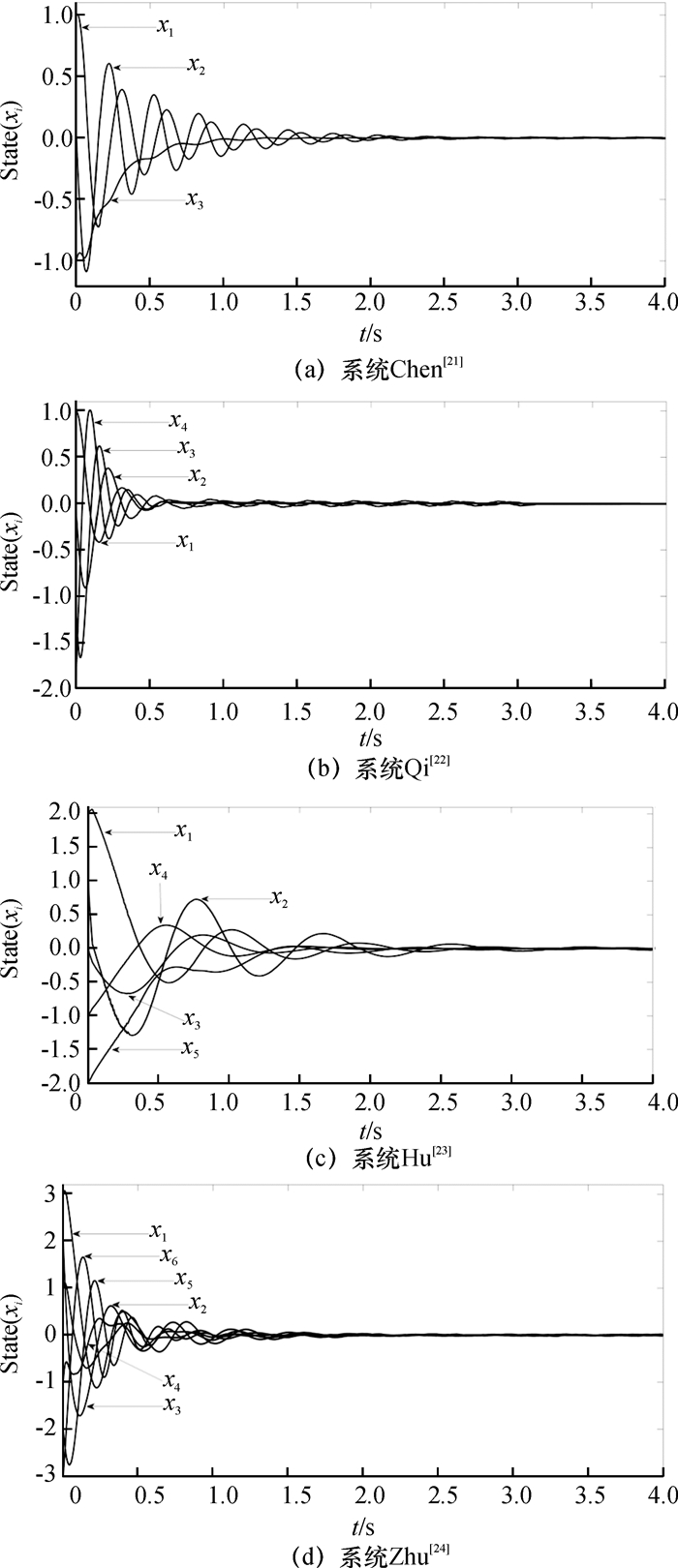
图 2 非线性控制器(9)反馈镇定各混沌系统的数值仿真图 Figure 2 Numerical simulation of stabilization for chaos via the nonlinear controller (9) |
图 2的数值仿真结果表明,对于非线性项含3次以上高次齐次函数的混沌系统,可用本文方法设计的非线性控制器自适应量化状态反馈镇定.
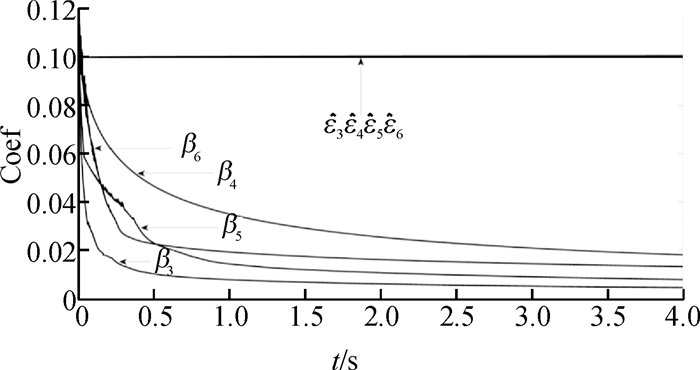
非线性控制器(9)反馈镇定Chen、Qi、Hu和Zhu混沌系统时,分别取时变量化器(5)的放大系数和估计误差界的初值为β(0)=0.1和
|
图 3 混沌控制系统的放大系数β(t)与估计误差界 |
反馈镇定混沌系统的过程引入量化机制后,闭环系统的稳定性和控制性能都可能发生变化,设计与量化器特性相关的非线性控制器,是实现和提高状态量化反馈控制系统稳定性的重要方法.本文设计了一种含具有时变参数的量化器的非线性控制器,可以较好地反馈镇定一类非线性项含高次齐次函数的混沌系统.本文对超过40个的3到6维的此类混沌系统进行了数值仿真,验证了本文方法的适用性.本文方法涵盖了文献[19]所采用的方法,使其成为本文方法的一个特例.大数据时代的来临,使得混沌及其控制的数字化具有越来越重要的意义,而量化是数字化中最重要的一环,未来有必要对基于量化机制的混沌、复杂混沌网络及其控制过程进行更加深入的研究.
| [1] |
Yu W. Finite-time stabilization of three- dimensional chaotic systems based on CLF[J].
Physics Letters A, 2010, 374(30): 3021-3024.
DOI: 10.1016/j.physleta.2010.05.040. |
| [2] |
Sun Y J, Wu Y B, Wang C C. Robust stabilization for a class of nonlinear systems via a single input control applicable to chaotic systems and its circuit implementation[J].
Chaos: An Interdisciplinary Journal of Nonlinear Science, 2013, 23(2): 023127.
DOI: 10.1063/1.4810928. |
| [3] |
Zhang R, Yang S. Stabilization of fractional-order chaotic system via a single state adaptive-feedback controller[J].
Nonlinear Dynamics, 2012, 68(1-2): 45-51.
DOI: 10.1007/s11071-011-0202-4. |
| [4] |
Chen G, Dong X. On feedback control of chaotic nonlinear dynamic systems[J].
International Journal of Bifurcation and Chaos, 1992, 2(02): 407-411.
DOI: 10.1142/S0218127492000392. |
| [5] |
Li P, Liu Y Z, Hu K L, et al. The chaotic control on the occasional nonlinear time-delayed feedback[J].
International Journal of Modern Physics B, 2004, 18(17-19): 2680-2685.
|
| [6] |
Hammami S, Benrejeb M, Feki M, et al. Feedback control design for Rö ssler and Chen chaotic systems anti-synchronization[J].
Physics Letters A, 2010, 374(28): 2835-2840.
DOI: 10.1016/j.physleta.2010.05.008. |
| [7] |
El-Dessoky M M, Yassen M T. Adaptive feedback control for chaos control and synchronization for new chaotic dynamical system[J]. Mathematical Problems in Engineering, 2012, Art. ID 347210, 12 pages.
http://cn.bing.com/academic/profile?id=567f8e289317b5a7353d9ac88352e997&encoded=0&v=paper_preview&mkt=zh-cn
|
| [8] |
Chen G. A simple adaptive feedback control method for chaos and hyper-chaos control[J].
Applied Mathematics and Computation, 2011, 217(17): 7258-7264.
DOI: 10.1016/j.amc.2011.02.017. |
| [9] |
Coutinho D F, Fu M, de Souza C E. Input and output quantized feedback linear systems[J].
Automatic Control, IEEE Transactions on, 2010, 55(3): 761-766.
DOI: 10.1109/TAC.2010.2040497. |
| [10] |
Fu M, Xie L. Finite-level quantized feedback control for linear systems[J].
Automatic Control, IEEE Transactions on, 2009, 54(5): 1165-1170.
DOI: 10.1109/TAC.2009.2017815. |
| [11] |
Ushio T, Hirai K. Chaotic behavior in piecewise-linear sampled-data control systems[J].
International Journal of Non-linear Mechanics, 1985, 20(5): 493-506.
|
| [12] |
Ushio T, Hsu C S. Simple example of digital control systems with chaotic rounding errors[J].
International Journal of Control, 1987, 45(1): 17-31.
DOI: 10.1080/00207178708933707. |
| [13] |
Delchamps D F. Stabilizing a linear system with quantized state feedback[J].
Automatic Control, IEEE Transactions on, 1990, 35(8): 916-924.
DOI: 10.1109/9.58500. |
| [14] |
Elia N, Mitter S K. Stabilization of linear systems with limited information[J].
Automatic Control, IEEE Transactions on, 2001, 46(9): 1384-1400.
DOI: 10.1109/9.948466. |
| [15] |
Fagnani F, Zampieri S. Quantized stabilization of linear systems: complexity versus performance[J].
Automatic Control, IEEE Transactions on, 2004, 49(9): 1534-1548.
DOI: 10.1109/TAC.2004.834111. |
| [16] |
Liberzon D, Hespanha J P. Stabilization of nonlinear systems with limited information feedback[J].
Automatic Control, IEEE Transactions on, 2005, 50(6): 910-915.
DOI: 10.1109/TAC.2005.849258. |
| [17] |
De Persis C. On feedback stabilization of nonlinear systems under quantization[C]//Decision and Control, 2005 and 2005 European Control Conference. CDC-ECC'05. 44th IEEE Conference on. [S. l. ]: IEEE, 2005: 7698-7703.
|
| [18] |
Liberzon D. Quantization, time delays, and nonlinear stabilization[J].
Automatic Control, IEEE Transactions on, 2006, 51(7): 1190-1195.
DOI: 10.1109/TAC.2006.878780. |
| [19] |
Tanasa V. Development of theoretical and computational tools for the design of control strategies for nonlinear sampled-data systems[D]. Paris: Université Paris Sud-Paris XI, 2012.
|
| [20] |
Wang Y H, Fan Y Q, Wang Q Y, et al. Adaptive feedback stabilization with quantized state measurements for a class of chaotic systems[J].
Communications in Theoretical Physics, 2012, 57(5): 808.
DOI: 10.1088/0253-6102/57/5/11. |
| [21] |
陈玉霞, 赵新渤. 一个新的三维混沌系统[J].
郑州轻工业学院学报:自然科学版, 2010, 25(5): 15-17, 20.
Chen Y X, Zhao X B. A new three-dimensional chaotic system[J]. Journal of Zhengzhou University of Light Industry, Natural Science Edition, 2010, 25(5): 15-17, 20. |
| [22] |
Qi G, Du S, Chen G, et al. On a four-dimensional chaotic system[J].
Chaos, Solitons & Fractals, 2005, 23(5): 1671-1682.
|
| [23] |
胡国四. 一类具有四翼吸引子的超混沌系统[J].
物理学报, 2009, 58(6): 3734-3741.
Hu G S. A family of hyperchaotic systems with four-wing attractors[J]. Acta Physica Sinica, 2009, 58(6): 3734-3741. DOI: 10.7498/aps.58.3734. |
| [24] |
朱建良, 张博亚, 孙鸣. 基于六维混沌的信号和图像加密研究[J].
信息技术, 2012(2): 106-108, 117.
Zhu J L, Zhang B Y, Sun M. Six-dimensional chaos based on signal encryption and image encryption[J]. Information Technology, 2012(2): 106-108, 117. |
| [25] |
Slotine J J E, Li W. Applied Nonlinear Control[M]. New Jersey: Prentice hall, 1991.
|
 2015, Vol. 32
2015, Vol. 32