2. 华南农业大学 信息学院,广东 广州 510246
2. College of Information, South China Agricultural University, Guangzhou 510246, China
多属性决策是指对具有多个属性的有限方案进行择优或排序问题[1],广泛地存在于社会生活和生产的各个方面[2-4].目前多属性决策问题已经引起国内众多学者的关注,他们分别采用前景理论[5]、后悔理论[6]、灰色理论[7]、理想点法[8]、粗糙集等理论与方法,从属性的类型(确实数、区间数、三角模糊数、梯形模糊数、混合型等)、决策主体的多寡(个人决策、群决策)、状态发生的概率(确定型、不确定型、风险型)等方面展开系列研究.上述决策理论与方法所建立的决策模型大多属于允许属性间进行支付的补偿模型.在这类模型中一个属性的改变能被其他属性的改变所抵消[9],然而实际决策过程中还存在不允许属性间支付的情况,“一票否决制”便是其中一种.在“一票否决制”情形下,只要任一属性没有达到要求时,无论其余属性达到何种优势,整个决策方案都将被否决.显然上述决策模型通常难以处理该类问题.在消错理论中该类多属性决策问题可表述为关键型多属性决策问题.虽然目前有占优法、最大最小法和最小最大法等模型可以处理“一票否决制”条件下的决策问题,但这些方法普遍存在信息利用不够全面、计算相对复杂等缺点.许多实验数据表明决策者在决策过程中具有错误损失规避心理[6],为此本文拟采用消错理论从减少和消除错误损失的角度对该类问题展开研究.
1 相关概念与定义消错理论是以错误为研究对象, 以减少和消除错误损失为研究目的的一种新型理论,其研究思路遵循了决策者规避错误损失的决策心理[10-14].根据消错理论的基本原理,相关的概念可界定如下.
定义1[15-16] 设U表示多属性决策问题,c为描述U的属性,C为属性集,c ∈ C,G为U上的一组确定且有资格的规则,若c不满足G的要求,则称c在U上对于规则G是错误的.
定义2[15-16] 设U表示多属性决策问题,c为描述U的属性,C为属性集,A为备选策略集,G为U上的一组确定且有资格的规则,令E={(a(c), G)|a∈A, c∈C},f:E→ R,则称f为定义在U上对于规则G的错误函数,简记为e=f(a(c)),其中R为实数域, e为策略a的属性c在规则G上的错误值.
定义3 设U为多属性决策问题,c为描述U的属性,C为属性集,c ∈ C,G为U上的一组确定且有资格的规则,若c发生错误时备选策略将被完全否决,那么称c为关键型属性.
根据定义3可知,“一票否决制”情形下的多属性决策问题中的任意一个属性均为关键型属性.这也正是“一票否决制”情形下多属性决策问题可以表述为关键型多属决策问题的原因.
2 基于消错理论的多属性决策方法 2.1 问题描述在关键型多属决策问题中,假设A ={a1, a2, …, am}表示由m个备选策略组成的策略集,C ={c1, c2, …, cn}表示由n个属性组成的属性集,xi, j为备选策略ai在属性cj下的值.根据属性的理想目标,属性通常可以分为效益型、成本型、区间型、固定型.其中效益型属性的属性值越大越好,成本型属性的属性值越小越好,区间型属性的属性值越接近某个区域越好,固定型属性的属性值越接近某个固定值越好.将效益型、成本型、区间型、固定型属性的集合分别记为C1、C2、C3、C4,相应下标的集合表示为N1、N2、N3、N4.显然有Ci
定义4 在关键型多属决策问题中,将至少在某一个属性上发生的备选策略称为非优策略.
定义5 在关键型多属决策问题中,将没有在任何一个属性上发生错误的策略称之为非劣策略.
假设用Ang表示非优策略集、用Anb表示非劣策略集,那么有Ang∪Anb=A,Ang∩Anb=ϕ,Ang=Anb.在关键型多属决策问题的决策过程中,非优策略将因“一票否决制”而被排除.在排除非优策略后,如果同时存在多个非劣策略则需进一步对非劣策略进行排序和选优.因此,关键型多属性决策问题的决策过程可以分为排劣和选优两大步骤.
2.2.1 排劣排劣是指将非优策略从备选策略集A中排除.其思路是依据“一票否决制”将存在一个或一个以上的属性发生错误的策略筛选出来并剔除.依据消错理论其具体步骤包括计算属性错误值和备选策略综合错误值两步.
(1) 计算属性错误值.
根据定义3可知,在关键型多属性决策问题中,只要有属性发生错误,无论错误值大小如何,备选策略都将被完全否决.显然,在这种情况下只需了解备选策略的各个属性是否发生错误,而无需精确计算错误的大小程度.当错误发生时用1表示,当错误没发生时用0表示,即采用经典错误函数(ran(f)={0, 1})来计算属性的错误值.假设属性cj的目标值为βj(当属性cj为区间型时,βj为区间数,βj=[βj-, βj+]),结合不同属性类型的特征,构建具体的错误函数如下.
① 效益型属性的错误函数
| $ {e_{i, j}} = f\left( {{x_{i, j}}} \right) = \left\{\begin{array}{l} 0, {\rm{}}\;\;{x_{i, j}} \ge {\beta _j}, \\ 1, {\rm{}}\;\;{x_{i, j}} < {\beta _j}, \end{array} \right. $ | (1) |
其中i =1, 2, …, m,j ∈ N1.效益型错误函数的曲线,如图 1(a)所示.
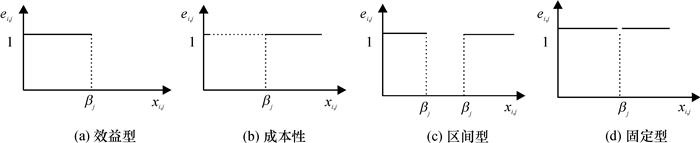
|
图 1 4类不同属性的错误函数 Figure 1 Error functions of four kinds of attributes |
② 成本型属性的错误函数
| $ {e_{i, j}} = f\left( {{x_{i, j}}} \right) = \left\{\begin{array}{l} 0, {\rm{}}\;\;{x_{i, j}} \le {\beta _j}, \\ 1, {\rm{}}\;\;{x_{i, j}} > {\beta _j}, \end{array} \right. $ | (2) |
其中i =1, 2, …, m,j ∈ N2.成本型错误函数的曲线,如图 1(b)所示.
③ 区间型属性的错误函数
| $ {e_{i, j}} = f\left( {{x_{i, j}}} \right) = \left\{\begin{array}{l} 1, {\rm{ }}\;\;\;\;\;{x_{i, j}} > \beta _j^ +, \\ 0, \;\;{x_{i, j}} \in \left[{\beta _{_j}^-, \beta _j^ +} \right], \\ 1, \;\;\;\;\;{x_{i, j}} < \beta _j^ -, \end{array} \right. $ | (3) |
其中i =1, 2, …, m,j ∈ N3.区间型错误函数的曲线,如图 1(c)所示.
④ 固定型属性的错误函数
| $ {e_{i, j}} = f\left( {{x_{i, j}}} \right) = \left\{\begin{array}{l} 0, {\rm{}}\;\;{x_{i, j}} = {\beta _j}, \\ 1, {\rm{}}\;\;{x_{i, j}} \ne {\beta _j}, \end{array} \right. $ | (4) |
其中i =1, 2, …, m,j ∈ N4.固定型错误函数的曲线,如图 1(d)所示.
(2) 计算策略综合错误值及排劣.
根据“一票否决制”的机理,结合错误逻辑(具体参见文献[17])和逻辑运算的规则,备选策略的ai的综合错误值可表示为
| $ {E_i} = {e_{i, 1}} \vee {e_{i, 2}} \vee \ldots \vee {e_{i, m}}, $ | (5) |
其中“∨”表示逻辑运算中的“并”.
根据逻辑运算规则Ei的取值要么为0,要么为1.显然,当综合错误值Ei =0时,表示备选策略ai不存在错误,ai为非劣策略;当综合错误值Ei =1时,表示备选策略ai至少有一个属性存在错误,ai为非优策略,应从备选策略中排除.显然,一个备选策略要么为非优策略要么为非劣策略,从备选策略集中剔除非优策略所剩下的策略均为非劣策略,即Anb=A-Ang.
2.2.2 选优剔除备选策略集中的非优策略后,如果剩下的非劣策略超过两个时,需要在非劣策略中进一步选出最佳策略.非劣策略在每个属性下都没发生错误,其某一属性值偏离错误(超越目标值)程度越大说明非劣策略在该属性下的表现越好.除固定型属性外,效益型、成本型和区间型属性都存在偏离错误的情况.根据错误函数(1)~(3)和定义5,可知非劣策略在效益型、成本型和固定型属性下的值分别是大于目标值βj、小于目标值βj和属于区间数[βj-, βj+].对于效益型属性,属性值xi, j越是大于目标值βj,错误偏离度越高;对于成本型属性,属性值xi, j越是小于目标值βj,错误偏离度越高;对于区域型属性,属性值xi, j越处于区间数[βj-, βj+]中间,错误偏离度越高.因此,构建式(6)这个函数对错误偏离度进行定量描述.
| $ \begin{array}{l} \;\;\;\;\;\;\;{d_{i,j}} = \\ \left\{ \begin{array}{l} 1 + \frac{{\left| {{x_{i,j}} - {\beta _j}} \right|}}{{{\beta _j}}},i \in {M_{nb}},j \in {\rm{ }}{N_1} \cup {N_2};\\ {\rm{min}}\{ 1 + \frac{{\left| {{x_{i,j}} - \beta _j^ - } \right|}}{{\beta _j^ - }},1 + \frac{{\left| {{x_{i,j}} - \beta _j^ + } \right|}}{{\beta _j^ + }}\} ,\\ \;\;\;\;\;\;\;\;\;\;\;\;i \in {M_{nb}},j \in {\rm{ }}{N_3}. \end{array} \right. \end{array} $ | (6) |
其中Mnb表示非劣策略的下标的集合.显然di, j是一个大于1的正数.
在决策过程中决策者除了有错误规避心理外,通常还会存在敏感性递减的情况.因此,可以构建式(7)这个函数来描述敏感性递减情况下的主观错误偏离度.
| $ d{\prime _{i, j}} = {\rm{ln}}{d_{i, j}}. $ | (7) |
对式(7)求导可知,一阶导数大于0、二阶导数小于0,也就是说式(7)是单调递增函数且递增速度边际递减,满足了敏感性递减的要求.对于关键型多属性决策问题,由于“一票否决制”机理的原因,只有各个属性均衡发展,才能使备选策略综合水平更优.因此,可以采用式(8)来计算非劣策略的总体错误偏离度.
| $ {D_i} = \sqrt[k]{{\prod\limits_{j \in {N_4}} {{{d'}_{i,j}}} }}, $ | (8) |
其中k表示非固定型属性的数量.显然,Di越大表示备选非劣策略越优.
2.2.3 决策步骤根据上述内容,关键型多属性消错决策方法可以分为两大步骤:
(1) 排劣,包括:①根据式(1)~(4)计算各备选策略在各属性下的错误值;②根据式(5)计算各策略综合错误值;③根据综合错误值判断非优策略,并将非优策略从备选策略集中剔除.若非劣策略大于等于两个时,则需要进行下一步.
(2) 选优,包括:①根据式(6)计算错误偏离度;②根据式(7)计算主观错误偏离度;③根据式(8)求得总体错误偏离度,并以选出最合适策略.
3 实例某市准备开展一项新市民信息行为调查活动,经过初步的调查和讨论共征集得a1、a2、a3、a4、a5、a6共6套调查方案.为了在备选方案中选择最适合方案,经过综合考虑规定必须同时满足以下5个方面(属性)的要求:(1) c1调查费用(万元),要求调查的费用不得超过50万元且越少越好;(2) c2抽查率(%):要求调查的抽查率必须超过1%且越高越好;(3) c3完成时间(d),要求调查活动必须在120 d内完成且越快越好;(4) c4满足比例要求数,要求所选取调查对象必须同时满足性别、年龄、职业和区域分布这4个方面相关的比例要求;(5) c5调查项目数,调查项目必须在20~30个之间(调查项目太少无法获取足够信息,调查项目太多将会提高调查的难度,从此影响调查的质量).各方案在上述5个属性上的测量值如表 1所示,求最佳方案.
| 表 1 决策矩阵 Table 1 Decision matrix |
显然上述问题是一个典型的关键型多属性决策问题,任一属性出错都会导致备选策略被“一票否决”.采用前景理论、后悔理论、灰色理论和理想点等方法是难以解决该问题的,而本文所提出的消错方法则能较好地解决该类问题.根据上述内容,可知属性c1和c3为成本型属性、c2为效益型、c4为固定型、c5为区间型.根据属性的类型,选择错误函数(1)~(4)可求得各备选策略在各属性下的错误值如表 2所示.根据各策略在各属性下的错误值,由式(5)可知E1=0、E2=0、E3=1、E4=1、E5=0、E6=0.因此,非优策略集Ang ={E3, E4}、Anb ={E1, E2, E5, E6}.由于非劣策略有4个,因此需要进一步进行选优步骤的计算.
| 表 2 错误值、错误偏离度和主观错误偏离度 Table 2 Error value, error deviation degree and subjective error deviation degree |
由式(6)可求得各备选策略在各属性下的错误偏离度如表 2所示;由式(7)可得主观错误偏离度如表 2所示;最后由式(8)可求得非劣策略的总体错误偏离度为D1=0.079 6、D2=0.159 2、D5=0.167 5、D6=0.显然,a5
本文从错误规避、敏感性递减的角度出发,利用消错理论,针对“一票否决制”多属性决策问题,提出了一种新型的多属性消错决策方法.该方法分为排劣和选优两个步骤.第1步,确立计算属性的错误值方法,在错误值的基础上计算备选策略的综合错误值,以此筛选出非优策略并将之从备选策略集中排除;第2步,计算非劣策略错误偏离度,并以此作为排序和选优的依据.最后通过“新市民信息行为调查活动”的例子,来说明本文所提出的关键型多属性消错决策方法能有效地解决“一票否决制”情形下的多属决策问题.
| [1] |
樊治平, 陈发动, 张晓. 基于前景理论的混合型多属性决策方法[J].
系统工程学报, 2012, 27(3): 295-301.
Fan Z P, Chen F D, Zhang X. Method for risky hybrid multiple attribute decision making based on prospect theory[J]. Journal of Systems Engineering, 2012, 27(3): 295-301. |
| [2] |
Véronique D, Karima S, François X L. A Bayesian network for recurrent multi-criteria and multi-attribute decision problems: Choosing a manual wheelchair[J].
Expert Systems with Applications, 2013, 40(7): 2541-2551.
DOI: 10.1016/j.eswa.2012.10.065. |
| [3] |
Arzu O. Practice over the private teaching institutions selection problem in one of secondary schools with using multiple attribute decision making method of topsis[J].
Procedia-Social and Behavioral Sciences, 2013, 89(10): 489-495.
|
| [4] |
Pradip P K, Subhankar K, Shyam R A. Technology assessment for wastewater treatment using multiple-attribute decision-making[J].
Technology in Society, 2012, 34(4): 295-302.
DOI: 10.1016/j.techsoc.2012.10.001. |
| [5] |
Fan Z P, Zhang X, Chen F D, et al. Multiple attribute decision making considering aspiration-levels: a method based on prospect theory[J].
Computers & Industrial Engineering, 2013, 65(2): 341-350.
|
| [6] |
张晓, 樊治平, 陈发动. 基于后悔理论的风险型多属性决策方法[J].
系统工程理论与实践, 2013, 33(9): 2313-2320.
Zhang X, Fan Z P, Chen F D. Method for risky multiple attribute decision making based on regret theory[J]. Systems Engineering-Theory & Practice, 2013, 33(9): 2313-2320. DOI: 10.12011/1000-6788(2013)9-2313. |
| [7] |
Wei G W. Grey relational analysis model for dynamic hybrid multiple attribute decision making[J].
Knowledge-Based Systems, 2011, 24(5): 672-679.
DOI: 10.1016/j.knosys.2011.02.007. |
| [8] |
Zhang Z, Guo C H. A method for multi-granularity uncertain linguistic group decision making with incomplete weight information[J].
Knowledge-Based Systems, 2012, 26(2): 111-119.
|
| [9] |
徐玖平, 吴巍.
多属性决策的理论与方法[M]. 北京: 清华大学出版社, 2006.
|
| [10] |
黄灏然, 郭开仲. 不确定性环境下消错决策方法的研究[J].
运筹与管理, 2013, 22(6): 99-104.
Huang H R, Guo K Z. Research on error-eliminating decision-making method under uncertainty[J]. Operations Research and Management Science, 2013, 22(6): 99-104. |
| [11] |
黄灏然, 郭开仲, 郑琦. 错误综合评价法的研究与应用[J].
中国管理科学, 2014, 22(4): 119-123.
Huang H R, Guo K Z, Zheng Q. Research and application of error comprehensive evaluation method[J]. Chinese Journal of Management Science, 2014, 22(4): 119-123. |
| [12] |
郭开仲, 闵惜琳. 消错规划求解研究[J].
广东工业大学学报, 2010, 27(1): 1-7.
Guo K Z, Min X L. A study of solution to the error-eliminating programming[J]. Journal of Guangdong University of Technology, 2010, 27(1): 1-7. |
| [13] |
Guo K Z, Li M. Research on decomposition of fuzzy error set[J].
Advances in Modelling A General Mathematics, 2006, 43(2): 1-2.
|
| [14] |
廖丽平, 郭开仲, 颜龙. 错误系统结构的毁灭变换研究[J].
广东工业大学学报, 2012, 29(4): 18-21.
Liao L P, Guo K Z, Yan L. A Study of destruction transformation of error system structures[J]. Journal of Guangdong University of Technology, 2012, 29(4): 18-21. |
| [15] |
Min X L, Guo K Z. A Primary probe on the application of error eliminating theory in urban traffic jam management system[J].
Advances in Systems Science and Applications, 2009, 9(3): 486-493.
|
| [16] |
郭开仲.
错误系统[M]. 北京: 科学出版社, 2012.
|
| [17] |
郭开仲.
错误逻辑[M]. 北京: 科学出版社, 2008.
|
 2015, Vol. 32
2015, Vol. 32