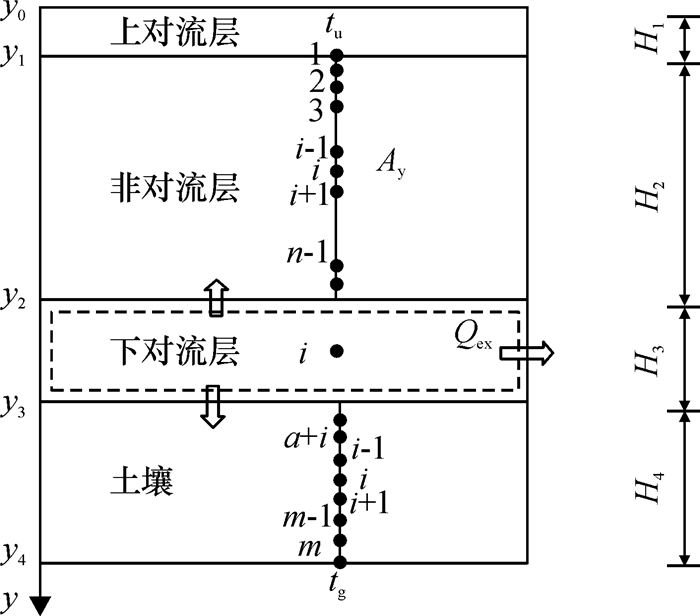
太阳池是一种收集和储存太阳能的溶液池,如图 1所示,通常太阳池由上对流层(Up convective zone, UCZ)、非对流层(Non-convective zone, NCZ)和下对流层(Lower convective zone, LCZ)构成.上对流层位于太阳池上层,此区域池水一般为浓度较低的清水,其主要作用是保护太阳池不受风的侵扰,同时能补充被太阳辐射热蒸发掉的水量.非对流层位于太阳池中部,在其溶液中热传递以导热方式为主,池水溶液在该层具有较稳定的盐度梯度.下对流层位于池的最底部,当太阳光照射到太阳池,很容易穿透上对流层的清水层而被漆成黑色的池底或以下层高浓度溶液吸收,从而加热池底部池水,此时中间非对流层就能对池底向上传递出来的热量起到抑制和保温作用.被底层池水吸收的热量就很难排出池外,从而被储存在下对流层区,随着太阳连续辐射,底层水将不断储热,这部分热量可以取出用作采暧、工业用热和发电等.
|
图 1 太阳池结构示意图 Figure 1 Schematic of solar pond structure |
自20世纪初第一个人工太阳池建成应用以来,太阳池的热质传递过程吸引了大量研究[1],数值计算方面,如赵建华等[2]采用数值方法建立了海水太阳池的二维数学模型,张红梅等[3]通过创建一维的数学模型,采用数值模拟与实验研究分析了池水浊度和池底反射率对太阳池热性能的影响,章庆丰和葛少成[4]采用有限差分法,模拟分析了太阳池非稳态热性能,王华等[5]采用数值计算与实验对比分析小型太阳池非稳态热质传递过程.有限容积法是通过积分方法,根据控制容积中通量平衡原则,而推导得出通量离散方程的一种方法.有限容积法因在离散方程时考虑通量平衡,而相对有限差分等数值方法更具物理意义,其离散过程也比其它方法复杂,然而目前现有太阳池数值分析研究中,很少采用有限容积方法.
同时由于太阳池在热带地区的应用与太阳池传统典型应用环境不同,因此近年来受研究者特别关注.例如,Srinivasan[6]通过总结对热带地区小型太阳池5年时间的运行经验,发现太阳池的热传输结构有可能会被池壁局部受热形成的对流区破坏,同时在热带丰富的雨季,及时向太阳池内补充盐水也是非常必要的.类似的研究还发现,在热带地下水较为丰富的区域,下对流层容易受地下水高水位的影响[7].近年太阳能利用技术在我国南方得到了广泛关注[8-10],太阳池在中国南方地区的应用也很早就吸引了大量的研究,但是在广东沿海地区的应用基础研究较少,然而太阳池技术在南方地区的推广有利于为水产养殖提供太阳能供热[11-12].
本文将采用有限容积方法,建立太阳池热质传递一维非稳态模型,并通过数值求解与现有实验数据比较,验证模型的正确性,同时采用湛江(21°183N, 110°383E)气象参数作为计算条件,分析太阳池在湛江地区应用时的热物性规律.
1 太阳池热质传递数学模型 1.1 热传递数学模型太阳池简化模型如图 1所示,坐标原点位于池面上方,y轴方向为池深度方向,假设太阳池壁面为绝热壁面,不考虑水平方向的热量传递,各层池水温度分布均匀,因此太阳池内热传递可简化为沿y轴方向的一维模型.现有研究表明,上对流层(UCZ)的池水温度近似等于大气温度,可作为求解非对流层热传递方程的第一类边界条件,因此,上对流层温度与大气温度近似相等[13]:
| $ {t_{\rm{u}}} = {t_\infty }\left( \tau \right). $ | (1) |
太阳池非对流层(NCZ)热传导控制方程为:
| $ \frac{\partial }{{\partial \tau }}\left( {\int\limits_V {{\rho _{\rm{w}}}{c_{{\rm{pw}}}}t{\rm{d}}V} } \right) = \int\limits_V {n\left( {{k_{\rm{w}}}{\rm{grad}}t} \right){\rm{d}}A} - \int\limits_V {\frac{{\partial I\left( {\tau ,y} \right)}}{{\partial y}}} dV. $ | (2) |
假设下对流层池水温度均匀且下对流层池壁作绝热处理,没有通过侧壁面热量损失,则下对流层能量平衡方程可表示为:
| $ \begin{array}{l} {\rho _{\rm{w}}}{c_{{\rm{pw}}}}{H_l}\frac{{\partial {t_1}}}{{\partial \tau }} = I\left( {\tau ,{y_2}} \right) - {k_{\rm{w}}}\frac{{\partial {\rm{t}}}}{{\partial {\rm{y}}}}\left| {_{y = {H_{\rm{u}}} + {H_{\rm{n}}}}} \right. - \\ {k_{\rm{g}}}\frac{{\partial {\rm{t}}}}{{\partial {\rm{y}}}}\left| {_{y = {H_{\rm{u}}} + {H_{\rm{n}}} + {H_{\rm{l}}}}} \right. - {Q_{{\rm{ex}}}}. \end{array} $ | (3) |
式(3)右边第1项为池水吸收的太阳能, W/m2;第2项为下对流层向非对流层传递的热量, W/m2;第3项为下对流层向土壤传递的热量, W/m2;第4项为下对流层热负荷, W/m2.
下对流层底部土壤层热传递控制方程:
| $ \frac{\partial }{{\partial \tau }}\left( {\int\limits_V {{\rho _{\rm{g}}}{c_{{\rm{pg}}}}t{\rm{d}}V} } \right) = \int\limits_A {n\left( {{k_{\rm{g}}}{\rm{grad}}t} \right){\rm{d}}A} . $ | (4) |
式(1)~(4)中t∞(τ)为池面上空大气瞬时温度, ℃;k为导热系数,W/m℃;ρ为密度, kg/m3; cp为定压比热容, J/kg℃; 下标w、g、u和l分别表示池水、土壤、上对流层和下对流层;tl为表示下对流层池水温度,℃;I(τ, y)为被池水吸收的太阳辐射能,W/m2;I(τ, y2)是被下对流层池水吸收的太阳能,W/m2.
根据Rabl和Nielsen[14]知池水吸收的太阳辐射能是池水深度的指数函数,I (τ, y)表达式为
| $ I\left( {\tau ,y} \right) = {I_0}\left( \tau \right)\theta \sum\limits_{j = 1}^4 {{\eta _j}\exp \left( { - {\mu _j}y} \right)} , $ | (5) |
式(5)中I0(τ)为到达池水液面的太阳辐射能;θ为池表面透射系数;ηj、μj为对应不同光波段的吸收系数,取值分别如表 1所示,池面透射系数θ可按式(6)计算:
| $ \theta = 1 - \frac{1}{2}\left[ {\frac{{{{\tan }^2}\left( {i - r} \right)}}{{{{\tan }^2}\left( {i + r} \right)}} + \frac{{{{\sin }^2}\left( {i - r} \right)}}{{{{\sin }^2}\left( {i + r} \right)}}} \right], $ | (6) |
| 表 1 不同可见光波段对应的ηj和μj Table 1 ηj and μj for different sunlight spectra |
式中i为入射辐射率相对于水平面的角度;r为入射辐射率相对于水平面的反射角.根据Snell法则[13]有
| $ \sin i = n\sin r, $ | (7) |
式(7)中n为折射率,水的折射率为1.33,同时i可通过式(8)计算:
| $ \cos i = \cos \delta \cos \varphi \cos \omega + \sin \delta \sin \varphi . $ | (8) |
式(8)中δ为倾斜角;φ为纬度;ω为时角,可通过式(9)计算:
| $ \omega = \frac{{2{\rm{ \mathsf{ π} }}\left( {h - 12} \right)}}{{24}}, $ | (9) |
式中h为时间.
为了简化计算,太阳辐射到达池面的辐射角假设与时间不相关,太阳假设位于春分点,此时h =14和φ =0,经分析由此假设引起的误差在5%以内, 将上述值代入式(6)~(9)可得i= 0.631 rad,r =0.460 rad和θ =0.977.
根据Aslan等人[15],选取当土壤表面的温度强度衰减至1/e(约0.37)时的土壤厚度为下对流层底部土壤计算区域.根据Kaufmann[16]太阳池水溶液的热物性参数是温度和浓度的函数,具有以下关系式:
| $ {k_{\rm{w}}} = 0.555\;3 - 8.13 \times {10^{ - 5}}c + 8 \times {10^{ - 4}}\left( {t - 20} \right), $ | (10) |
| $ {\rho _{\rm{w}}} = 998 + 0.65c - 0.4\left( {t - 20} \right), $ | (11) |
| $ {c_{{\rm{pw}}}} = 4180 + 4.396c + 0.004\;8{c^2}, $ | (12) |
式中c为盐水质量百分比浓度,c=S/ρ×100%,S为盐水质量浓度,kg/m3.
根据Aslan等人[15]的文献,土壤参数为kg=0.96 W/m℃,ρgCg=2.09×106J/m3℃.
1.2 质传递数学模型假设太阳池四壁均为绝质条件,计算前池内初始浓度满足稳定线性分布,同时上层有连续的海水注入,上对流层盐水初始浓度, cUCZ=1%,下对流层盐水初始浓度, cLCZ=18%[17],则非对流层浓度控制方程可表示为
| $ \frac{\partial }{{\partial \tau }}\int\limits_V {c{\rm{d}}V} = \int\limits_A {n\left( {D{\rm{grad }}c} \right){\rm{d}}A} , $ | (13) |
式中D为质扩散系数,m2/s.
根据Giestas和Joyce[17]知,池水温度在5~100 ℃,浓度在0%~20%范围内的质扩散系数满足以下规律:
| $ \begin{array}{l} D = \left( {8.16 + 0.255t + 2.5 \times {{10}^{ - 3}}{t^2} - 0.028c + } \right.\\ \left. {1.47 \times {{10}^{ - 3}}{c^2}} \right) \times {10^{ - 10}}. \end{array} $ | (14) |
上述控制方程采用全隐格式进行离散化,网格分布如图 1所示.其中Δy1和Δy2分别是非对流层和土壤区域网格尺寸.非对流层计算区域采用100个网格点,土壤层计算区域采用100个网格点.时间步长Δt=0.25 d.方程(1)的离散格式为
| $ \begin{array}{l} \int\limits_{\Delta V} {\left[ {\int\limits_\tau ^{\tau + \Delta \tau } {{\rho _{\rm{w}}}{c_{{\rm{pw}}}}t{\rm{d}}\tau } } \right]{\rm{d}}V} = \\ \int\limits_\tau ^{\tau + \Delta \tau } {\left[ {\int\limits_A {\vec n\left( {{k_{\rm{w}}} \cdot {\rm{grad}}t} \right){\rm{d}}A} } \right]{\rm{d}}\tau } - \int\limits_\tau ^{\tau + \Delta \tau } {\left[ {\int\limits_{\Delta V} {\frac{{\partial I\left( {\tau ,y} \right)}}{{\partial y}}{\rm{d}}V} } \right]{\rm{d}}\tau } . \end{array} $ | (15) |
方程(3)可离散为
| $ \begin{array}{l} {\left( {{\rho _{\rm{w}}}{c_{{\rm{pw}}}}} \right)_l}{H_3}\frac{{{t_l} - t_l^0}}{{\Delta \tau }} = - {k_{l - 1/2}}\frac{{{t_l} - {t_n}}}{{\Delta y}} - {k_{l + 1/2}}\frac{{{t_l} - {t_g}}}{{\Delta y}} + \\ I\left( {\tau ,{y_2}} \right) - {Q_{{\rm{ex}}}}. \end{array} $ | (16) |
方程(4)和(13)可分别离散为
| $ \int\limits_{\Delta V} {\left[ {\int\limits_\tau ^{\tau + \Delta \tau } {{\rho _{\rm{g}}}{c_{{\rm{pg}}}}t{\rm{d}}\tau } } \right]{\rm{d}}V} = \int\limits_\tau ^{\tau + \Delta \tau } {\left[ {\int\limits_A {\vec n\left( {{k_{\rm{g}}}{\rm{grad}}t} \right){\rm{d}}A} } \right]{\rm{d}}\tau } , $ | (17) |
| $ \int\limits_{\Delta V} {\left[ {\int\limits_\tau ^{\tau + \Delta \tau } {c{\rm{d}}\tau } } \right]{\rm{d}}V} = \int\limits_\tau ^{\tau + \Delta \tau } {\left[ {\int\limits_A {\vec n\left( {D{\rm{grad}}c} \right){\rm{d}}A} } \right]{\rm{d}}\tau } . $ | (18) |
上述离散方程可简化为
| $ - {\alpha _{i - 1}}{t_{i - 1}} + {\alpha _i}{t_i} - {\alpha _{i + 1}}{t_{i + 1}} = \alpha _i^0t_i^0 + {S_c}, $ | (19) |
式中上标0表示τ时刻的变量,而没有上标的变量表示τ +Δτ时刻值,方程(19)的各项系数值如表 2所示.上述离散化方程采用三对角矩阵法逐项迭代求解.
| 表 2 离散化方程的系数 Table 2 Coefficient of discretized equation |
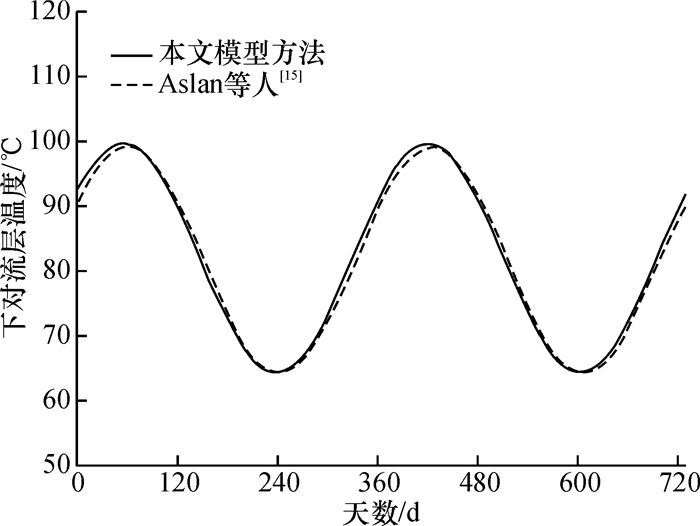
为了验证上述数值模型的正确性,本文选用Aslan等人[15]的数值工况进行求解并对比验证,该工况假设太阳池各层区域分布稳定,各区域深度值分别为固定值,空气温度和太阳辐射强度分别是时间的周期性三解函数,本文所选数值工况各项参数详见表 3所示.图 2所示为本文模型方法求解Aslan等人[15]得到的下对流层池水温度与Aslan等人[15]结果的对比图.如图 2所示,两种方法计算得到的下对流层温度均是时间的周期性三角函数且两种方法的结果误差小于5%,这充分验证本文模型方法的正确性.
|
图 2 下对流层温度结果比较 Figure 2 Comparison of LCZ temperature |
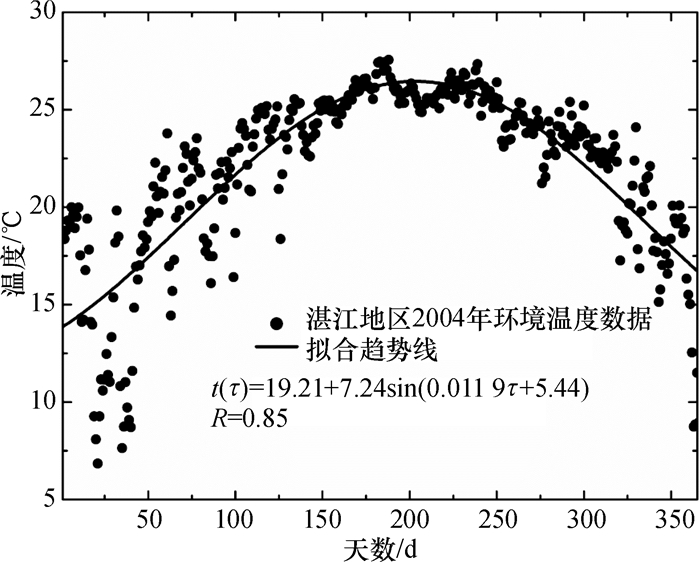
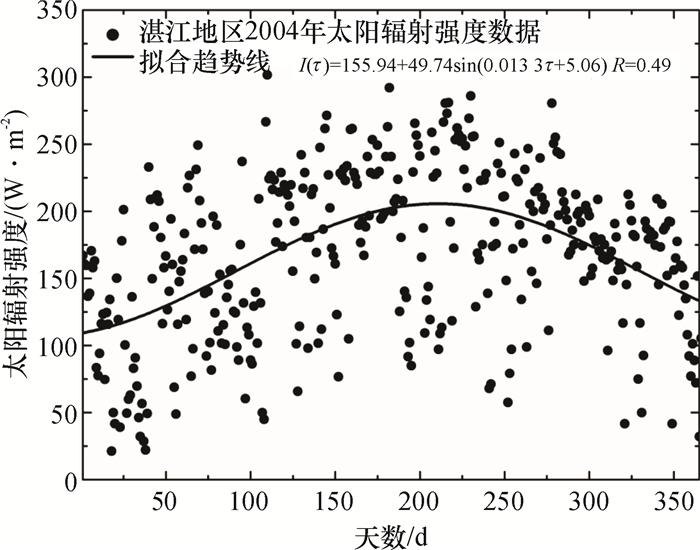
本文为了推广应用该模型方法,并分析太阳池在湛江热带地区的适用性,将以Aslan等人[15]的太阳池结构为基础,同时为了避免实际应用中潮湿土壤及地下水位对太阳池运行影响,计算时假设下对流层底部已采取防潮及绝热措施,不考虑土壤层传热影响,下对流层底部边界条件为绝热绝质边界.选取湛江地区2004年全年室外环境温度和太阳辐射强度数据,采用最小二乘法拟合,分别得到室外环境温度和太阳辐射强度与时间的周期性三角函数关系式,然后将其作为模型计算的边界条件.环境温度和太阳辐射强度数据的拟合结果分别如图 3和图 4所示.通过对离散数据的拟合分析,环境温度和太阳辐射强度分别是时间的周期性三角函数,函数表达式分别如图中公式所示.计算时热负荷函数为太阳辐射强度的倍数,定义如下:
| $ {Q_{{\rm{ex}}}}\left( \tau \right) = 155.94n + 49.74n\sin \left( {1.99 \times {{10}^{ - 7}}\tau } \right), $ | (20) |
|
图 3 湛江地区2004年日平均空气温度 Figure 3 Daily average temperature of Zhanjiang city in 2004 |
|
图 4 湛江地区2004年日平均太阳辐射强度 Figure 4 Daily average radiation intensity of Zhanjiang city in 2004 |
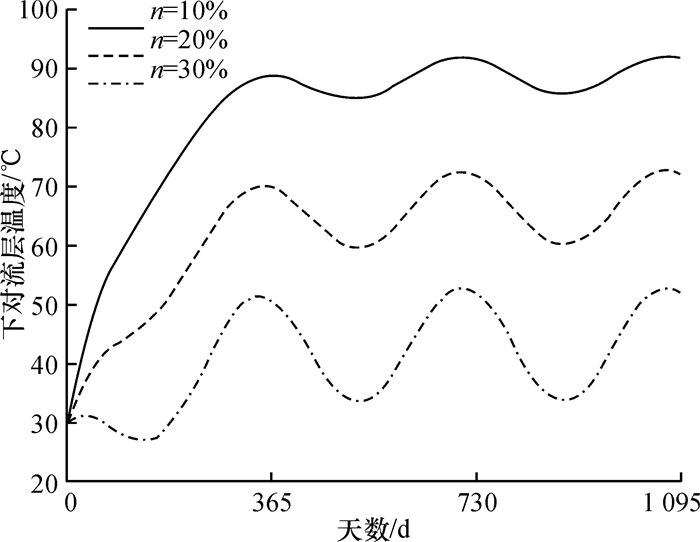
式中n为百分数值.Tabor[1]通过研究深度为2 m深的太阳池,建议太阳池取热时最佳热负荷倍数n为15%~25%,Jaefarzadeh[13]在分析太阳池非稳态热传递时,同时考虑太阳池侧壁阴影效果的影响,其结果建议n取10%~20%.本文针对湛江地区气候参数,分别研究n取值10%~30%时太阳池热物性规律.计算得到的下对流层(LCZ)池水温度如图 5所示.结果表明,随着n增加,下对流层池水温度逐渐降低,当n =10%时,下对流层池水平均温度约85 ℃,而当n =30%时,池水平均温度约为40 ℃.这说明当太阳池其他各项参数不变时,热负荷越高,底部下对流层池热量存储的越少,下对流层池水平均温度将越低.
|
图 5 湛江地区太阳池不同热负荷工况的下对流层温度 Figure 5 LCZ temperature of Zhanjiang solar pond in different heatloads cases |
为了定性分析和优化太阳池结构,假定太阳池深度为2 m保持不变,本节通过改变非对流层厚度,分析太阳池热物性特性,其中定义非对流层深度的比例为
| $ {R_{\rm{H}}} = \frac{{{H_2}}}{{{H_2} + {H_3}}}. $ | (21) |
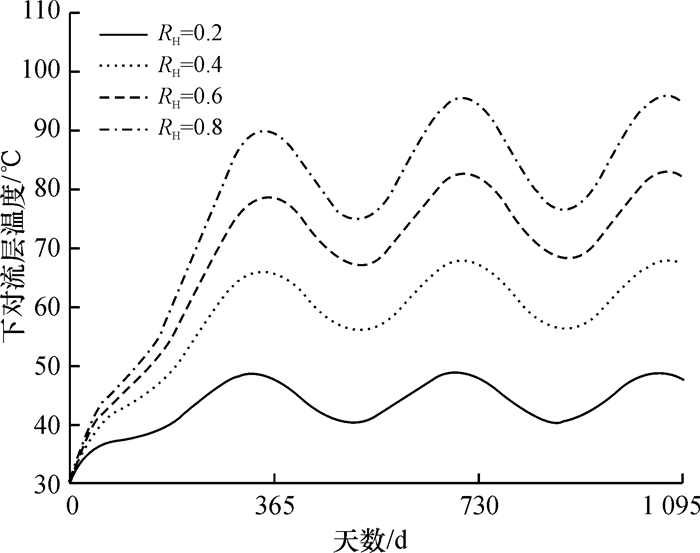
在计算不同RH值时,H1=0.15m保持不变,环境温度和太阳辐射强度取2.1节中湛江地区参数的拟合函数,热负荷为n=20%时的公式(20),计算得到的不同太阳池非对流层厚度的下对流层温度如图 6所示.结果表明,随着RH升高,下对流层池水温度逐渐升高,当RH=0.8时,下对流层池水平均温度约为85 ℃,而RH=0.2时,约43 ℃,这说明当热负荷一定时,增加非对流层厚度,相当于为下对流层增加保温层,从而通过非对流层的热损失将越少,池水温度也将越高.
|
图 6 湛江地区太阳池结构优化工况的下对流层温度 Figure 6 LCZ temperature of Zhanjiang solar pond in optimal structure cases |
本文采用有限容积数值计算方法,建立一维非稳态海水太阳池热质传递模型,动态描述太阳池蓄热和取热过程.同时采用湛江地区2004年的大气环境温度和太阳辐射数据为计算条件,定性分析了海水太阳池在湛江地区应用时的热物性能,主要结论如下:
(1) 采用有限容积法,建立一维非稳态太阳池热质传递模型,并通过与已公开发表的典型数值工况结果对比,验证模型方法的正确性.
(2) 应用模型方法,以湛江地区2004年气象参数为计算条件,分析太阳池在湛江地区应用时,不同热负荷的太阳池热物性.结果表明深度为2 m的太阳池,下对流层池水温度随热负荷增加而降低,n此时取10%~20%最佳.同时还应用模型方法计算不同太阳池非对流层厚度的工况,结果表明太阳池下对流层池水温度随非对流层厚度比例增加而上升,考虑实际太阳池结构稳定和下对流层不可能无限制小,实际非对流层比例RH建议取0.4~0.6.
| [1] |
Tabor H. Solar ponds[J].
Solar energy, 1981, 27(3): 181-194.
DOI: 10.1016/0038-092X(81)90120-1. |
| [2] |
赵建华, 孙文策, 解茂昭, 等. 海水太阳池二维数学模型[J].
大连理工学报, 2005, 45(1): 32-35.
Zhao J H, Sun W C, Xie M Z, et al. A two-dimensional mathematical model of seawater solar pond[J]. Journal of Dalian University of Technology, 2005, 45(1): 32-35. |
| [3] |
张红梅, 解茂昭, 孙文策, 等. 盐梯度太阳池热性能模拟及实验研究[J].
工程热物理学报, 2006, 27(1): 65-68.
Zhang H M, Xie M Z, Sun W C, et al. Simulation and experimement of thermal performance of a salt-gradient solar pond[J]. Journal of Engineering Thermophysics, 2006, 27(1): 65-68. |
| [4] |
章庆丰, 葛少成. 太阳池的非稳态热性能的数值模拟[J].
辽宁工程技术大学学报, 2007, 26(6): 809-812.
Zhang Q F, Ge S C. Numerical simulation of unsteady heat performance of solar pond[J]. Journal of Liaoning Technical University, 2007, 26(6): 809-812. |
| [5] |
王华, 孙文策, 邹家宁. 小型太阳池瞬态传热传质[J].
太阳能学报, 2009, 30(1): 33-37.
Wang H, Sun W C, Zou J N. Transient heat and mass transfer in small scale solar pond[J]. Acta Energiae Solaris Sinica, 2009, 30(1): 33-37. |
| [6] |
Srinivasan J. Performance of a small solar pond in the tropics[J].
Solar Eenergy, 1990, 45(4): 221-230.
DOI: 10.1016/0038-092X(90)90090-Y. |
| [7] |
Wang Y F, Akbarzadeh A. A parametric study on solar ponds[J].
Solar Energy, 1983, 30(6): 555-562.
DOI: 10.1016/0038-092X(83)90067-1. |
| [8] |
卜其辉, 秦红, 梁振南, 等. 直膨式太阳能热泵系统特性分析及优化[J].
广东工业大学学报, 2010, 27(2): 61-64.
Bu Q H, Qin H, Liang Z N, et al. Characteristic analysis and optimization of direct-expansion solar-assisted heat pump system[J]. Journal of Guangdong University of Technology, 2010, 27(2): 61-64. |
| [9] |
王长宏, 林涛, 林明标, 等. 太阳能温差发电系统热电性能的分析[J].
广东工业大学学报, 2011, 28(2): 47-50.
Wang C H, Lin T, Lin M B, et al. Analysis of thermoelectric properties of the solar thermal power system[J]. Journal of Guangdong University of Technology, 2011, 28(2): 47-50. |
| [10] |
王璋元, 杨晚生, 张向美, 等. 居住建筑光热系统一体化技术问题研究[J].
广东工业大学学报, 2013, 30(4): 121-124.
Wang Z Y, Yang W S, Zhang X M, et al. Problems with the integrated solar hot water systems in the domestic buildings in china and the related suggestions[J]. Journal of Guangdong University of Technology, 2013, 30(4): 121-124. |
| [11] |
蒙沛南, 郑宏飞, 钟水库, 等. 太阳池为水产品越冬养殖供热的研究[J].
广西大学学报:自然科学版, 1997, 22(2): 114-117.
Meng P N, Zheng H F, Zhong S K, et al. The study on a solar pond suppling thermal for water-producats during the winter[J]. Journal of Guangxi University: Nature Science Edition, 1997, 22(2): 114-117. |
| [12] |
蒙沛南, 郑宏飞, 周科. 圆形斜壁氯化镁溶液太阳池的蓄热性能研究[J].
太阳能学报, 1998, 19(3): 277-281.
Meng P N, Zheng H F, Zhou K. Study on the thermal storage performance of the round inclined wall MgCl2 solution solar ponds[J]. Acta Energiae Solaris Sinica, 1998, 19(3): 277-281. |
| [13] |
Jaefarzadeh M R. Thermal behavior of a small salinity-gradient solar pond with wall shading effect[J].
Solar Energy, 2004, 77(3): 281-290.
DOI: 10.1016/j.solener.2004.05.013. |
| [14] |
Rabl A, Nielsen C E. Solar ponds for space heating[J].
Solar Energy, 1975, 17(1): 1-12.
|
| [15] |
Aslan H E, Salam A, Probert S D, et al. Predicted performances of a proposed coffered solar pond[J].
Applied Energy, 1984, 16(4): 283-306.
DOI: 10.1016/0306-2619(84)90004-7. |
| [16] |
Kaufmann DW. Sodium Chloride[M]. New York: Reinhold, 1960.
|
| [17] |
Giestas M, Joyce A. The influence of non-constant diffusivities on solar ponds stability[J].
International Journal of Heat and Mass Transfer, 1997, 40(18): 4379-4391.
DOI: 10.1016/S0017-9310(97)00050-1. |
 2015, Vol. 32
2015, Vol. 32