直流无刷电机(Brushless DC Motor, BLDCM)具有结构简单、效率高、输出转矩大、精度高、稳定性好、低噪声、寿命长、易于维护等特点, 使之在电动汽车、航空航天、家用电器、办公自动化等方面有着广泛的应用[1].传统的BLDCM需要霍尔信号提供转子信息, 但是霍尔信号会受到温度、磁场等的影响, 这不仅增加了电机的体积和成本, 而且降低了系统的可靠性.因此, 直流无刷电机的无位置传感器控制在近些年一直是研究的热点.
无位置传感器直流无刷电机的控制方式一般利用电机的电流、电压等间接获得转子位置信息, 无位置传感器无刷直流电机控制技术目前最为成熟的是基于反电动势的过零点检测法[1-4].然而反电动势过零点检测法在电机处于静止时, 电动势为0, 处于低速状态下, 反电动势的电压很低, 因此难以获得可靠的转子位置, 因此必须使用其他的起动方法加速至一定的速度, 再切换至反电动势法运行.
无位置传感器直流无刷电机起动常用的方式有外同步起动方式、三段式起动方式等[5-8].外同步方式是通过改变频率方式使转子旋转加速直到能够稳定检测到反电动势[9], 但这种起动方式会由于电机的静摩擦力和负载变化出现振动、反转甚至起动失败.三段式起动方式[10-11]系统起动时, 任意给定一组脉冲, 只要保证在气隙中形成方向不变的磁通幅值, 经过一定的时间转子会被强行定位在合磁场的方向, 实现预定位.然后通过外同步方式进行加速.该方法在转子预定位时, 会由于惯性转子到达定位平衡点以后并不立刻静止而是在平衡点附近作摆动, 引起电机的震动.同时还会受到电机参数、外施电压和负载条件的影响, 可能会导致在起动时出现反转.
为了克服转子定位出现的问题, 提出了基于定子铁芯饱和法[12-14]来检测转子的初始位置.通过对定子绕组施加固定脉宽的检测脉冲, 检测电流的变化率[12]或者检测电流的峰值[15-16].该方法可以提供精确的转子位置信息, 但是对检测相电流的器件的精度要求比较高, 成本也比较高.同时需要在施加检测脉冲时检测, 由于定子绕组的时间常数会随着温度变化, 需要对检测到的电流进行温度补偿.另外一种检测初始位置的方法是施加检测脉冲后, 检测定子绕组放电的时间[17], 该方法实现比较简单, 但是只能用于静止时位置的检测.文献[18]提出向电机的绕组注入3次检测脉冲, 前两次导通任意两相, 检测比较导通续流时非导通相的电压, 并且记录相应的电流值.确定转子位置相差180°电角度区间, 根据测得的电感值再确定第3次的导通相, 比较3次电流的记录值, 确定转子位置在30°电角度的范围内.但是该方法需要同时检测相电压和母线电流, 因此不适用于低成本的控制器中.
本文从检测两相导通续流时得出的非导通相电压的变化规律出发, 提出一种基于电感法转子静止时进行位置区间检测的优化设计.此方法低速状态下同样适用, 能够实现无位置传感器的无刷直流电机的起动.
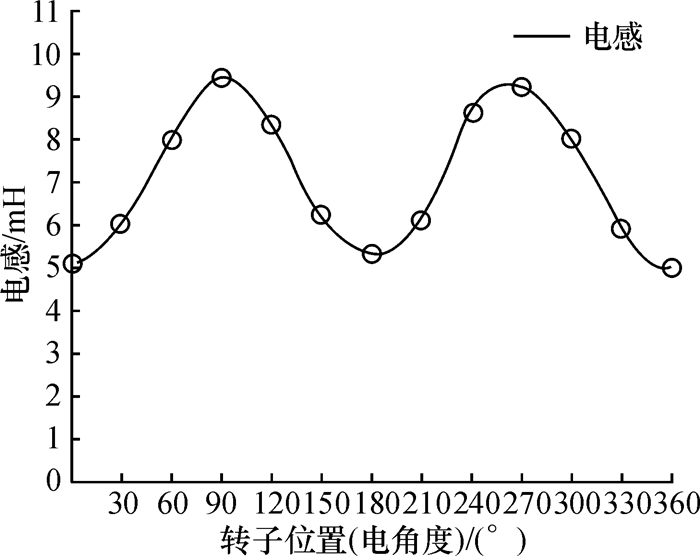
1 初始位置检测转子位置检测的基本原理是由转子位置引起定子铁芯的饱和效应和定子铁芯非线性磁化的特性.任何带铁芯的电感线圈, 在忽略磁滞和涡流影响后, 电流、磁通的关系为:电感L不再是一个常量, 当外界磁场作用于电感时, L随着铁芯线圈内部磁通的变化而变化.当转子N极与电流产生的磁场方向一致时, 产生增磁作用, 磁路饱和增加, 电感L减少; 当转子N极与电流产生的磁场方向相反时, 饱和减弱, 电感L增加:即定子铁芯的电感值和转子位置呈一定的函数关系.转子位置和电感的关系如图 1所示.
|
图 1 转子位置(电角度)和电感关系 Figure 1 Relationship between rotor position and inductances |
BLDC相电压方程为
| $ {u_{\rm{x}}} = R{i_{\rm{x}}} + L\frac{{{\rm{d}}{i_{\rm{x}}}}}{{{\rm{d}}t}} + {e_{\rm{x}}}, $ | (1) |
式中, ux为相电压, ix为相电流, ex为反电动势.
当电机处于静止状态时反电动势为0, 则式(1)可以改写为
| $ {u_{\rm{x}}} = R{i_{\rm{x}}} + L\frac{{{\rm{d}}{i_{\rm{x}}}}}{{{\rm{d}}t}}. $ | (2) |
静止状态时的电流为
| $ i\left( t \right) = \frac{{{u_{\rm{x}}}}}{R}\left( {1 - {{\rm{e}}^{ - \frac{t}{\tau }}}} \right), $ | (3) |
式中
由于直流无刷电机的等效电阻比较小, 相电压可以改写为
| $ {u_{\rm{x}}} \cong L\frac{{{\rm{d}}{i_{\rm{x}}}}}{{{\rm{d}}t}}. $ | (4) |
不同的转子位置会导致绕组电感变化, 引起非导通相端电压在导通和续流阶段有规律的变化.可通过测量非导通相的电压来进行初始位置的判断以及换向时刻的确定.初始位置检测分为两个阶段:电感比较确定转子相对位置阶段和NS极性确定阶段.
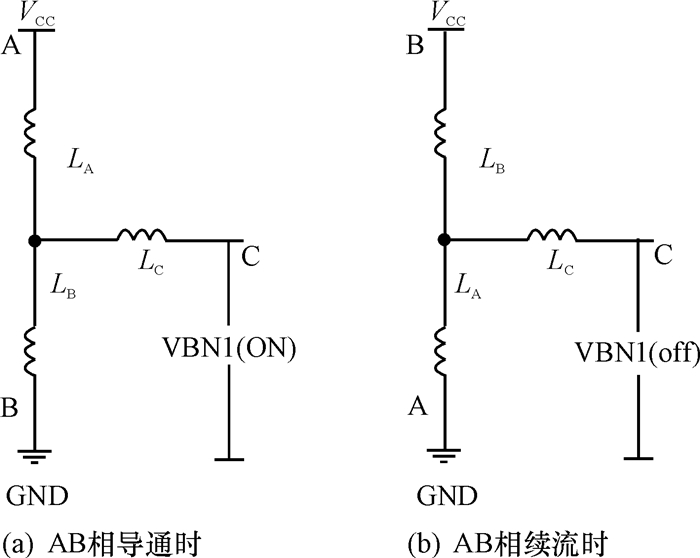
1.1.1 A、B相导通和续流时C相端电压方程[10]在A、B相导通期间, C相为非导通相.如图 2(a)所示.
|
图 2 AB相导通和续流 Figure 2 Pulse injecting interval and freewheeling interval between A and B phases |
由方程(4)可知
| $ \left\{ \begin{array}{l} {V_{{\rm{AN1}}\left( {{\rm{on}}} \right)}} = \frac{{{L_{\rm{A}}}}}{{{L_{\rm{B}}} + {L_{\rm{A}}}}}{V_{{\rm{DC}}}},\\ {V_{{\rm{NB1}}\left( {{\rm{on}}} \right)}} = \frac{{{L_{\rm{B}}}}}{{{L_{\rm{B}}} + {L_{\rm{A}}}}}{V_{{\rm{DC}}}}, \end{array} \right. $ | (5) |
式中, VAN1(on)、VNB1(on)分别为导通时A相电压和B相电压, LA、LB、LC分别是A相、B相和C相的电感, VDC为母线电压.
在A、B相续流期间, 如图 2(b).
| $ \left\{ \begin{array}{l} {V_{{\rm{BN1}}\left( {{\rm{off}}} \right)}} = \frac{{{L_{\rm{B}}}}}{{{L_{\rm{B}}} + {L_{\rm{A}}}}}{V_{{\rm{DC}}}},\\ {V_{{\rm{NA1}}\left( {{\rm{off}}} \right)}} = \frac{{{L_{\rm{A}}}}}{{{L_{\rm{B}}} + {L_{\rm{A}}}}}{V_{{\rm{DC}}}}, \end{array} \right. $ | (6) |
式中, VBN1(off)、VNA1(off)分别为导通时A相电压和B相电压.
由式(5)、(6)可得
| $ {V_{{\rm{NA1}}\left( {{\rm{off}}} \right)}} - {V_{{\rm{NB1}}\left( {{\rm{on}}} \right)}} = \frac{{{L_{\rm{A}}} - {L_{\rm{B}}}}}{{{L_{\rm{B}}} + {L_{\rm{A}}}}}{V_{{\rm{DC}}}}. $ | (7) |
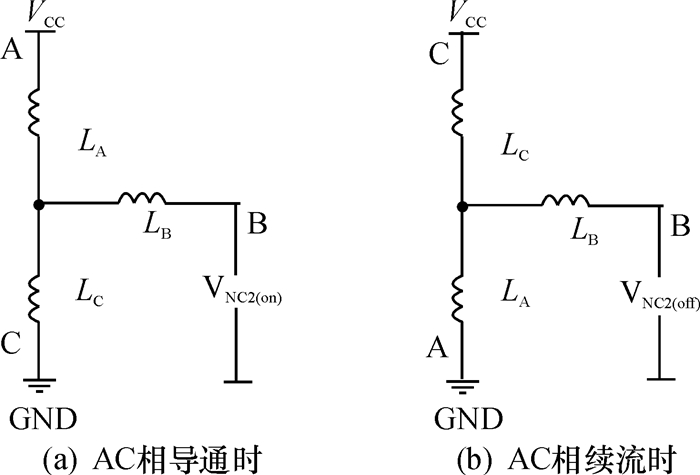
当A、C相导通续流时, B相为非导通相, 如图 3(a)、(b)所示.
|
图 3 AC相导通和续流 Figure 3 Pulse injecting interval and freewheeling interval between A and C phases |
同理可得
| $ {V_{{\rm{NA2}}\left( {{\rm{off}}} \right)}} - {V_{{\rm{NC2}}\left( {{\rm{on}}} \right)}} = \frac{{{L_{\rm{A}}} - {L_{\rm{C}}}}}{{{L_{\rm{C}}} + {L_{\rm{A}}}}}{V_{{\rm{DC}}}}, $ | (8) |
式中VNC2(on)为导通时的C相端电压, VNA2(off)为续流阶段A相的端电压.
| $ {V_{{\rm{NB1}}\left( {{\rm{on}}} \right)}} - {V_{{\rm{NC2}}\left( {{\rm{on}}} \right)}} = \frac{{\left( {{L_{\rm{B}}} - {L_{\rm{C}}}} \right){L_{\rm{A}}}}}{{\left( {{L_{\rm{C}}} + {L_{\rm{A}}}} \right)\left( {{L_{\rm{B}}} + {L_{\rm{A}}}} \right)}}{V_{{\rm{DC}}}}. $ | (9) |
由式(7)、(8)、(9)可以得出电感值的大小关系.即可确定转子的相对位置, 如图 4所示.

|
图 4 电感大小和转子位置的关系 Figure 4 Relationship between inductance size and rotor position |
在不受转子磁场的影响时, 三相的电感LA、LB、LC是相等的.式(5)中
| $ {V_{{\rm{NB1}}\left( {{\rm{on}}} \right)}} = \frac{1}{2}{V_{{\rm{DC}}}}. $ | (10) |
当转子N极与电流产生的磁场方向一致时, 产生增磁作用, 磁路饱和增加, 电感L减小; 当转子N极与电流产生的磁场方向相反时, 饱和减弱, 电感L增加.该阶段加入的时间脉冲应该比第一阶段的检测脉冲长, 以使得定子绕组的磁路达到饱和.
在导通脉冲的开始时和结束时对未导通相分别进行电压检测.在导通脉冲开始时VNB1(on)约
通过以上步骤可以确定转子的位置.根据位置信息导通相应的电机进行加速, 检测转子位置、加速, 直到能够稳定检测到反电动势.本实验采取两两导通方式, 6个导通状态形成的磁动势如图 5所示.用3位二进制数表示转子一个周期内的6个位置[11].本文采用向电机施加一长一短脉冲进行加速和定位的方法.施加长脉冲时, 在换向后的前30°电度角范围内, 只要检测导通相电感的大小关系, 一旦检测到电感的关系有变化, 就要施加短时脉冲来进行定位.否则继续施加长脉冲进行加速.

|
图 5 磁动势 Figure 5 Magnetic motive force |
假设转子位于位置1, 即LA = LB, LB=LC, LA>LB>LC区间内, 而且电机逆时针旋转.能够产生正转动力矩的是A+B-和A+C-, 对电机施加一长一短脉冲, 即对电机施加A+B-长脉冲, 进行加速, 记录B相电压.长脉冲结束后施加A+C-短脉冲进行定位, 如果检测到的C相电压小于B相的记录电压则继续对电机施加相同的脉冲.一旦检测到C相电压和记录的B相电压相等, 即可换向, 向电机施加A+C-的长脉冲进行加速, 检测LA与LC的关系, 如果LA >LC, 继续施加A+C-的长脉冲, 否则施加B+C-的短脉冲进行定位.
3 切换至反电动势控制当电机加速到一定的速度, 就可以稳定地检测到反电动势.这样就可以转换到反电动势控制的方法.为了使电机不会产生振动甚至失步, 必须选择正确的切换点.电机加速到可以稳定检测到反电动势时, 使电机转子维持在一个稳定的速度.在每次的换向时刻开始计时, 记录在该导通状态下的时间.在下一次的换向时刻保存该时间T1, 同时检测非导通相反电动势是否位于过零点.如果在一个机械周期的换向时刻能够检测到非导通相的反电动势位于过零点就可以进行切换, 否则进行调整电压脉冲占空比, 直到换向时刻检测到非导通相的过零点.
本文选取57BL02型的直流无刷电机作为实验对象, 来验证本文理论的正确性.该电机为三相星型结构, 额定电压为24V, 额定电流2A, 额定转速3 000 r/min.试验的控制系统的芯片为dsPIC33JFMC204.
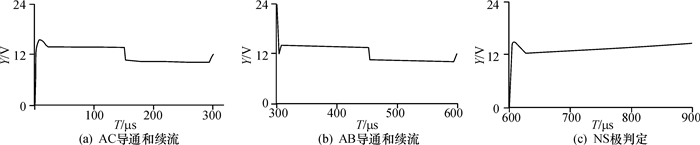
为了验证在两相导通和续流期间非导通相的端电压随转子位置的变化规律, 以θ=25°进行为例进行实验.实验方法如图 6所示.图 6(a)在AC相导通时测得B端的电压
|
图 6 θ=25°时的实验结果 Figure 6 The result when θ=25° |
本文的无位置起动方法是基于转子位置对饱和定子铁芯的影响, 只需要对电机加入3次PWM脉冲, 即可得到转子位置的信息.加速时加入一长一短脉冲, 分别进行加速和定位.加速至稳定检测到反电动势的时候切换至反电动势控制策略.试验结果表明, 用本文阐述的方法实现了静止时转子位置的估计, 也能够在低速时正确地估计换向时刻.经过以上的实验测试, 说明了本文所提出的方法在实际应用中有一定的效果.
| [1] |
吴志勇. 基于绕组电感变化特性的直流无刷电机无位置传感器控制[D]. 天津大学电气与自动化工程学院, 2011.
|
| [2] |
Taeyeon K, Chungil K, Joon L. A new sensorless drive scheme for a bldc motor based on the terminal voltage difference[C]//IECON 2011-Conference of 37th Annual Conference of the IEEE Industrial Electronics Society. Piscataway: IEEE, 2011: 1710-1715.
|
| [3] |
李自成. 无刷直流电机无位置传感器控制关键技术研究[D]. 华中科技大学自动化学院, 2010.
|
| [4] |
吴曙光. 无位置传感器无刷直流电机起动控制研究[D]. 天津大学电气与自动化工程学院, 2008.
|
| [5] |
许鹏, 曹建波, 曹秉刚. 无位置传感器直流无刷电机软件起动[J].
电机与控制学报, 2009, 13(5): 734-738.
Xu P, Cao J B, Cao B G. Software starting for brushless DC motor with-out position sensor[J]. Electric Machines and Control, 2009, 13(5): 734-738. |
| [6] |
易慧斌. 无位置传感器无刷直流电机起动方法研究[D]. 西南交通大学电气工程学院, 2012.
|
| [7] |
庞延庆. 无位置传感器无刷直流电动机位置检测与起动问题的研究[D]. 山东大学电气工程学院, 2006.
|
| [8] |
李树栋. 无位置传感器无刷直流电机启动方法的研究[D]. 江苏科技大学电子信息学院, 2010.
|
| [9] |
Cheng K Y, Tzou Y Y. Design of a sensorless commutation IC for BLDC motors[C]//Power Electronics Specialists Conference. Piscataway: IEEE, 2002: 295-300.
|
| [10] |
吴筱辉, 程小化, 刘杰. 反电势法检测转子位置的无刷直流电机起动方法[J].
微电机, 2005, 38(4): 20-89.
Wu X H, Cheng X H, Liu J. The start- ing method's of the BLDC motor using back emf to monitor the rotor position[J]. Micromotors, 2005, 38(4): 20-89. |
| [11] |
王思远. 无刷直流电动机的反电动势换相及起动方法的研究[D]. 哈尔滨工业大学电气工程及自动化学院, 2006.
|
| [12] |
Jang G H, Park J H. Position detection and start-up algorithm of a rotor in a sensorless BLDC motor utilizing inductance variation[C]//Electric Power Applications IEEE Proceedings. Piscataway: IEE E, 2002: 137-142.
|
| [13] |
Lee W J, Sul S K. A new starting method of BLDC motors without position sensor[C]//Industry Applications, IEEE Transactions on. Piscataw ay: IEEE, 2006: 1532- 1538.
|
| [14] |
Chang Y C, Tzou Y Y. A new sen- sorless starting for brushless dc motors with- out reversing rotation[C]//Power Electronics Specialists Conference. Piscataway: IEEE, 2007: 619-624.
|
| [15] |
Lai Y S, Shyu F S. New initial position detection technique for three-phase brushless DC motor without position and current sensors[C]//In- dustry Applications, IEEE Transactions on. Piscat away: IEEE, 2003: 485-491.
|
| [16] |
林明耀, 刘文勇, 周谷庆. 无位置传感器无刷直流电机短时脉冲定位加速方法[J].
电工技术学报, 2011, 26(9): 80-86.
Lin M Y, Liu W Y, Zhou G Q. A location and acceleration method of sensor- less brushless DC motor utilizing short voltage p-ulse short voltage pulse[J]. Transactions of China Electrotechnical Society, 2011, 26(9): 80-86. |
| [17] |
Sugawara J, Kaimori T, Nishikata S. A novel and simple initial rotor position detecting method for PMSMs[C]//Power Electronics and Drives Systems. Piscataway: IEEE, 2005: 612-617.
|
| [18] |
Champa P, Somsiri P, Wipasuramonton P. Initial rotor position estimation for sensorless brushless DC drivers[J].
IEEE Transactions on Industry Applications, 2009, 45(4): 1318-1324.
DOI: 10.1109/TIA.2009.2023355. |
 2015, Vol. 32
2015, Vol. 32