2. 广东工业大学 应用数学学院, 广东 广州 510520;
3. 广东省电信规划设计院有限公司 研发中心, 广东 广州 510630
2. School of Applied Mathematics, Guangdong University of Technology, Guangzhou 510520, China;
3. Research and Developing Center, Guangdong Planning and Designing Institute of Telecommunications Co., Ltd., Guangzhou 510630, China
近年来, 随着第4代移动通信技术的逐步成熟, 4G网络已经获得了全球范围内的商业部署.根据NTT DoCoMo提供的大量数据表明, 70%的高速数据业务, 尤其是高速下载类的业务, 发生在室内环境中.因而TD-LTE室内分布系统的建设行将成为网络规划重点中的重点[1-3].
现有的室内分布系统主要采用人工设计方式和智能规划软件设计方式.其中人工设计的网络质量很大程度上依赖于工程师的专业水平和工作经验, 而且需要反复地勘测、设计和修改, 周期较长, 耗费大量人力、物力和财力[4-10].而智能规划软件设计方式是基于抽象设计方案建立数学模型, 并通过设计相应的数学算法进行求解, 该方式具有操作简便, 规划所需时间短等优点.目前比较成熟的室内规划模型以及算法都是基于2G和3G的网络系统, 通过建立数学模型, 并对其进行求解, 求出室内分布系统所需器件的类型及其布放位置.文献[11]分析了GSM室内分布的设计思路, 建立了以花费最低和实际天线口功率与需求的偏差最小为目标的数学模型, 最后针对该模型提出了相应的算法.但是该模型只是针对2G的网络进行的建模, 4G网络与2G网络有很大的差异性.文献[12-13]建立了一类基于GSM室内分布系统的TD-SCDMA室内分布系统的数学模型, 同时结合该模型提出倒推遍历寻找合路点和启发式确定最优拓扑的求解算法.但是该模型只是针对TD-SCDMA的系统, 对于TD-LTE并没有通用性.文献[14]在概括各个室内分布系统共同特点的前提下, 着重对设计过程的功率和链路算法进行了详尽分析, 建立了平层功率估算和主干功率估算模型.但是该模型并不能精确得到完整的室内分布系统的原理图.以上模型和算法不能完全适用于TD-LTE系统, 但对TD-LTE的室内分布方法具有很重要的指导性作用.目前国内TD-LTE室内覆盖系统的设计大多还是以理论分析为主.文献[15]依据TD-LTE室内覆盖需求, 对TD-LTE室内覆盖的建设方式进行了研究分析, 重点分析了单通道和双通道两种模式, 并给出了这两种模式相应的应用场景.文献[16]分析了TD-LTE的室内覆盖解决方案和技术要求, 着重对各制式间的干扰进行了简单的剖析, 并给出解决干扰的建议.文献[15-16]没有给出较好的数学模型来描述TD-LTE室内分布系统.
科学的室内分布系统是在保证室内用户的通话质量的前提下降低建设成本, 减轻室外宏站负荷, 减少业务拥塞, 增大网络容量, 系统化提高移动通信网络的服务水平, 提升用户感知.本文在总结室内分布系统规划研究的基础上, 提出一种基于MIMO双通道建设的多目标数学模型.该模型在保证TD-LTE室内分布系统的双通道功率平衡的条件下, 实现所花成本和所耗功率最低.同时, 由于4G室内分布系统优化问题的候选器件多且每个器件的选择类型多, 是一类组合优化问题[10-11], 其解空间大, Pareto最优解少, 导致寻优过程十分复杂, 计算量非常巨大.本文设计了一种基于M2M种群分解策略的算法, 能够精确地找到有效解.
1 TD-LTE室内分布系统数学模型本文根据TD-LTE室内分布覆盖系统的规范要求, 设计一路合路和一路新建的MIMO双通道无源室内分布系统.模型的建立是以设计好的合路一路的天线口实际功率为基础, 作为新建一路相匹配的天线口功率的输入, 使得新建一路与合路一路每对MIMO天线的功率之差在一定的范围内.工程经验表明, 当两路通道的功率之差为3dB时系统容量减少8%, 当两路功率相差为5dB时系统容量减少30%.
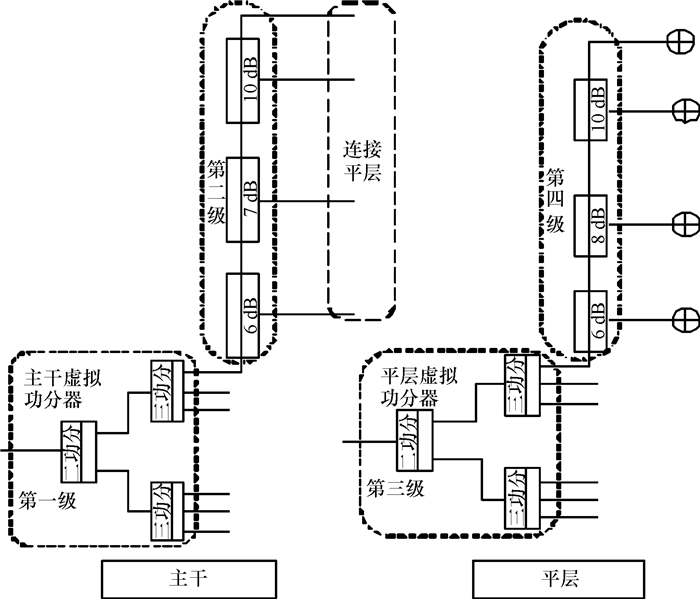
1.1 新建通道模型流程图新建通道模型流程如图 1所示, 该模型是以合路一路的天线布放位置、天线口功率作为新建一路的输入条件, 两路通道天线口功率差异限制在3dB作为约束.新建通道分为主干和平层, 共有四级模式组成.其中一级、二级在主干上, 三级、四级在平层上.如图 2所示, 一级由一个到多个功分器组成的虚拟功分器组成, 二级是使用耦合器来对不同的平层分不同的功率, 三级与主干的第一级相同, 四级是使用耦合器来对不同的天线分不同的功率.

|
图 1 新建一路建模流程图 Figure 1 The new way of modeling flow chart |
|
图 2 主干、平层四级模式 Figure 2 Four modes of the main way and floor |
模型的已知条件和输入:
建筑物信息(楼层高度, 层数)、室内基站信息(输出功率, 位置)、合路一路信息(天线的实际功率, 位置)、馈线、耦合器、功分器类型和损耗.
假设模型的符号表示:
Q:楼层的层数; q:信源的输入功率;
M1:馈线的种类; M2:耦合器的种类;
c1, j:第j种馈线的价格;
c2, j:第j种耦合器的价格;
E1, j:第j种馈线百米损耗;
E2, j, 1:第j种耦合器的插出损耗;
E2, j, 2:第j种耦合器的插损损耗;
N1, k:第四级第k平层的馈线数目;
N2, k:第四级第k平层的耦合器数目;
N3, k:第四级第k平层的天线数目;
N1:第二级馈线数目; N2:第二级耦合器数目;
W0:第一级中虚拟功分器的每路损失;
Wi:第三级中第i个楼层的虚拟功分器的每路损失;
I:信源与虚拟功分器之间的电缆长度;
Li:第二级的第i段馈线的长度;
Li, k:第四级的第k平层内第i段馈线的长度;
Hi, k:新建一路的第k平层的第i个天线的输出功率;
ei, k:合路一路的第k平层的第i个天线对应的实际功率;
xj:第一级即信源与虚拟功分器的馈线连接选择第j种, 其中选中为1, 不选中为0;
xi, j:第二级的第i段馈线选择第j种, 其中选中为1, 不选中为0;
xi, j, k:第四级中第k平层中第i段馈线选择第j种, 选中为1, 不选中为0;
yi, j:第二级第i个耦合器选择第j种, 其中选中为1, 不选中为0;
yi, j, k:第四级中第i个耦合器选择第j种, 选中为1, 不选中为0.
模型变量:
xj={0, 1}, j=1, 2, …, M1.
xi, j={0, 1}, j=1, 2, …, M1, i是第二级内馈线编号;
xi, j, k={0, 1}, j=1, 2, …, M1, i是第四级第k平层馈线编号;
yi, j={0, 1}, j=1, 2, …, M2, i是第二级内耦合器编号;
yi, j, k={0, 1}, j=1, 2, …, M2, i是第四级第k平层耦合器编号.
该数学模型的目标函数有两个:所有器件总成本f1最小化和所有器件损耗功率f2最小化.
| $ \begin{array}{l} {f_1} = \sum\limits_{k = 1}^Q {\left( {\sum\limits_{j = 1}^{{M_1}} {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over x} }_{j,k}}{c_{1,j}}} + \sum\limits_{i = 1}^{{N_{1,k}}} {\sum\limits_{j = 1}^{{M_1}} {{x_{i,j,k}}{c_{1,j}}} } + } \right.} \\ \left. {\sum\limits_{i = 1}^{{N_{4,k}}} {\sum\limits_{j = 1}^{{M_1}} {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }_{i,j,k}}{c_{1,j}}} } + \sum\limits_{i = 1}^{{N_{2,k}}} {\sum\limits_{j = 1}^{{M_2}} {{y_{i,j,k}}{c_{2,j}}} } } \right) + \sum\limits_{j = 1}^{{M_1}} {{x_j}{c_{1,j}}} + \\ \sum\limits_{i = 1}^{{{\bar N}_1}} {\sum\limits_{j = 1}^{{M_1}} {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }_{i,j}}{c_{1,j}}} } + \sum\limits_{i = 1}^{{{\bar N}_2}} {\sum\limits_{j = 1}^{{M_2}} {{{\bar y}_{i,j}}{c_{2,j}}} } . \end{array} $ |
| $ \begin{array}{l} {f_2} = \sum\limits_{k = 1}^Q {\left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over L} }_k}\sum\limits_{j = 1}^{{M_1}} {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over x} }_{j,k}}{E_{1,j}}} + \sum\limits_{i = 1}^{{N_{1,k}}} {{L_{i,k}}\sum\limits_{j = 1}^{{M_1}} {{x_{i,j,k}}{E_{1,j}}} } + } \right.} \\ \left. {\sum\limits_{i = 1}^{{N_{4,k}}} {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over L} }_{i,k}}\sum\limits_{j = 1}^{{M_1}} {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }_{i,j,k}}{E_{1,j}}} } + \sum\limits_{i = 1}^{{N_{2,k}}} {\sum\limits_{j = 1}^{{M_2}} {{y_{i,j,k}}{E_{2,j,1}}} } } \right) + I\sum\limits_{j = 1}^{{M_1}} {{x_j}{E_{1,j}}} + \\ \sum\limits_{i = 1}^{{{\bar N}_1}} {{{\bar L}_i}\sum\limits_{j = 1}^{{M_1}} {{{\bar x}_{i,j}}{E_{1,j}}} } + \sum\limits_{i = 1}^{{{\bar N}_2}} {\sum\limits_{j = 1}^{{M_2}} {{{\bar y}_{i,j}}{E_{2,j,1}}} } . \end{array} $ |
约束条件:
(1) 选择性约束.馈线和耦合器必须选且只能选择一种, 表示如下.
| $ \begin{array}{l} \sum\limits_{j = 1}^{{M_1}} {{x_j}} = 1,\sum\limits_{j = 1}^{{M_3}} {{{\bar z}_{i,j}}} = 1,\sum\limits_{j = 1}^{{M_2}} {{{\bar y}_{i,j}}} = 1\;\sum\limits_{j = 1}^{{M_1}} {{{\bar x}_{i,j}}} = 1,\\ \sum\limits_{j = 1}^{{M_1}} {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over x} }_{i,j}}} = 1,\sum\limits_{j = 1}^{{M_3}} {{z_{i,j,k}}} = 1,\sum\limits_{j = 1}^{{M_2}} {{y_{i,j,k}}} = 1,\sum\limits_{j = 1}^{{M_1}} {{x_{i,j,k}}} = 1,\\ \sum\limits_{j = 1}^{{M_1}} {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }_{i,j,k}}} = 1. \end{array} $ |
(2) MIMO双通道功率平衡约束.新建一路与合路一路的天线口功率之差在3dB范围内.
| $ \left| {{H_{i,k}} - {e_{i,k}}} \right| \le 3{\rm{dB}}, $ |
i=1, 2, …, (第i层天线总数), k=1, 2, …, (楼层总数).
Hi, k是一个比较复杂的公式.如:
| $ \begin{array}{l} {H_{1,1}} = q - I\sum\limits_{j = 1}^{{M_1}} {{x_j}{E_{1,j}}} - {W_0} - {{\bar L}_3}\sum\limits_{j = 0}^{{M_1}} {{{\bar x}_{3,j}}{E_{1,j}}} - \\ \sum\limits_{j = 0}^{{M_2}} {{{\bar y}_{3,j}}{E_{2,j,2}}} - {{\bar L}_2}\sum\limits_{j = 0}^{{M_1}} {{{\bar x}_{2,j}}{E_{1,j}}} - \sum\limits_{j = 0}^{{M_2}} {{{\bar y}_{2,j}}{E_{2,j,2}}} - \\ {{\bar L}_1}\sum\limits_{j = 0}^{{M_1}} {{{\bar x}_{1,j}}{E_{1,j}}} - \sum\limits_{j = 0}^{{M_2}} {{{\bar y}_{1,j}}{E_{2,j,1}}} - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over L} }_1}\sum\limits_{j = 1}^{{M_1}} {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over x} }_{1,j}}{E_{1,j}}} - {W_1} - \\ {L_{3,1}}\sum\limits_{j = 0}^{{M_1}} {{x_{3,j,1}}{E_{1,j}}} - \sum\limits_{j = 0}^{{M_2}} {{y_{3,j,1}}{E_{2,j,2}}} - {L_{2,1}}\sum\limits_{j = 0}^{{M_1}} {{x_{2,j,1}}{E_{1,j}}} - \\ \sum\limits_{j = 0}^{{M_2}} {{y_{2,j,1}}{E_{2,j,2}}} - {L_{1,1}}\sum\limits_{j = 0}^{{M_1}} {{x_{1,j,1}}{E_{1,j}}} - \sum\limits_{j = 0}^{{M_2}} {{y_{1,j,1}}{E_{2,j,1}}} - \\ {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over L} }_{1,1}}\sum\limits_{j = 1}^{{M_2}} {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }_{1,j,1}}{E_{1,j}}} . \end{array} $ |
总成本f1最低是指主干和平层所有的器件和馈线的成本之和最小; 总功率f2最低是指主干和平层所有器件和馈线的损耗的功率最小.选择性约束指所有器件和馈线可选且只能选择一种; 双通道平衡约束指新建的和合路的实际的天线口的功率之差在3dB范围内, 这样才能达到系统的性能.
2 求解算法本文建立以各级耦合器、功分器等器件的成本以及电缆的成本和价格为两个目标函数整数规划问题, 此数学模型属于组合优化领域中的整数规划问题.它是线性规划的一种特殊形式.此问题的解空间大, Pareto最优解少, 寻优过程十分复杂.依据本文模型的特征, 设计了一种基于M2M种群分解策略的算法, 该算法能够保持解的种群多样性, 精确地找到有效解.
M2M算法框架的主要思想是将一个复杂的多目标优化问题分解为一系列简单的多目标优化子问题来求解, 并且在一次运行中同时解决这些子问题.实际的操作是把种群分解为一系列的子种群, 让每个子种群都对应一个子问题, 子种群通过相互协作来求解其相应的子问题从而实现原来多目标优化问题的求解[17].
M2M算法用一组方向向量来实现种群的分解, 首先在目标向量空间中给出K个单位方向向量v1, v2, …, vK, 计算每个个体与方向向量的夹角, 把个体分到与方向向量的夹角最小的方向向量所代表的子区域中.
M2M算法框架的主要步骤为:
Step1:初始化.初始化的种群并将种群分到K个子区域中的子种群P1, P2, …, PK.
Step2:杂交变异.在每一个子区域中产生新个体.
Step3:选择.运用选择策略在每一个子区域中选择出新的子种群.
其中初始化的种群的个体采用整数编码方式, 每个元素表示相应位置的耦合器或馈线选用型号.假设有m个耦合器n条馈线的类型需要确定, 耦合器、馈线的类型分别为M、N种.则个体的左边m个元素表示对应位置的耦合器的类型, 右边n个元素表示对应位置的馈线的类型.
例如对于个体V:
| $ V = \left( {{v_1},{v_2},{v_m}, \cdots ,{v_n}} \right), $ |
其中1≤vi≤M, vi为整数.当i≤m时, vi表示第i个耦合器的类型为vi; 当i>m时, vi表示第i-m条馈线的类型为vi.
M2M算法框架种群的分解方法简单有效, 只需要给出一组方向向量就能实现种群的分解.从上面的算法框架中得出, 可以使用不同的选择策略来实现子种群个体的更新.
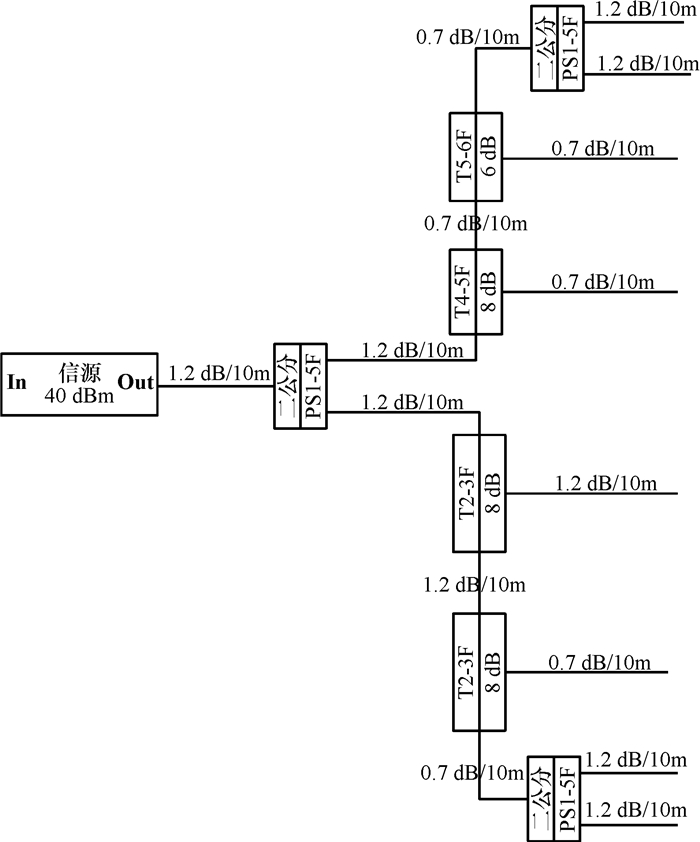
3 仿真实验对本文提出的模型采用基于M2M种群分解策略的算法, 在Matlab2007b上进行了仿真实验, 将算法应用到实际室内分布设计中, 假设实际的楼层数目为8层, 从第一到第八层的天线的数目分别为8、6、8、6、8、6、8、8.由于采用多目标优化算法, 因此仿真可以得到一组Pareto最优解, 现在给出有代表性的1个解实现的室内分布, 如图 3和图 4所示.

|
图 3 第一楼层室内分布图 Figure 3 Indoor distribution diagram of First floor |
|
图 4 主干室内分布图 Figure 4 Indoor distribution diagram of main way |
从图 3和图 4可以看出第一个楼层的合路一路和新建一路的天线口功率之差都在3dB范围内, 其他的楼层的仿真结果也和第一楼层的结果相类似, 可以达到整个系统性能的要求.
4 总结本文分析了TD-LTE室内分布的设计思路, 开创性地建立了一个多目标的室内分布模型, 然后针对该模型提出了基于M2M种群分解策略的算法.该模型和算法能够有效解决TD-LTE室内分布系统设计这一高难度的组合优化问题, 为TD-LTE室内分布系统提供了一种智能化的解决方案.
| [1] |
肖清华, 汪丁鼎, 许光斌.
TD_LTE网络规划设计与优化[M]. 北京: 人民邮电出版社, 2013: 318-360.
|
| [2] |
蒋远, 汤利民.
TD-LTE原理与网络规划设计[M]. 北京: 人民邮电出版社, 2012: 286-312.
|
| [3] |
高泽华, 高峰, 林海涛.
室内分布系统规划与设—GSM/TD-SCDMA/TD-LTE/WLAN[M]. 北京: 人民邮电出版社, 2013: 79-89.
|
| [4] |
吴为.
无线室内分布系统实战必读[M]. 北京: 机械工业出版社, 2012: 17-68.
|
| [5] |
Rappaport T S. Wireless communications second edition:principles and practice[M]. Beijing: Publishing House of electronics industry, 2013: 617-669.
|
| [6] |
田野, 陈欣, 雷德华. TYCAD在室内覆盖设计中的应用[J].
移动通信, 2009, 14(1): 62-64.
Tian Y, Chen X, Lei D H. TYCAD application in design of indoor coverage[J]. The mobile communication, 2009, 14(1): 62-64. |
| [7] |
田野, 尹东彬. 一种基于CAD平台的室内覆盖设计方法: 中国, 101719175 A[P]. 2010-06-02.
|
| [8] |
王鹏. 通信工程室内覆盖设计系统的研究和实现[D]. 成都: 电子科技大学信息与软件工程学院, 2009.
|
| [9] |
李铭, 刘海林. 3G网络规划中覆盖与容量的关系[J].
广东工业大学学报, 2008, 25(4): 83-85.
Li M, Liu H L. The relationship between coverage and capacity of 3G network planning[J]. Journal of Guangdong University of Technology, 2008, 25(4): 83-85. |
| [10] |
丁远, 刘海林. 3G网络覆盖范围的参数规划及可视化仿真[J].
广东工业大学学报, 2008, 25(2): 47-50.
Ding Y, Liu H L. 3G network coverage planning and visualization of simulation parameters[J]. Journal of Guangdong University of Technology, 2008, 25(2): 47-50. |
| [11] |
李炯城, 易永鑫, 孙黎辉. 室内分布系统的设计和优化[J].
无线通信, 2009, 9(10): 25-29.
Li J C, Yi Y X, Sun L H. Indoor converage system design and optimization[J]. Wireless Communication, 2009, 9(10): 25-29. |
| [12] |
肖恒辉, 李祥鹰, 李炯城. 一类TD-SCDMA室内分布系统的设计[C]//中国通信学会通信建设工程技术委员会2010年年会论文集. 北京: [出版者不详], 2010: 89-95.
|
| [13] |
肖恒辉, 李炯城, 孙黎辉. 2G/3G共网的室内分布系统优化[J].
无线通信, 2009, 43: 22-23.
Xiao H H, Li J C, Sun L H. The optimization of 2G/3G network indoor converage system[J]. Wireless Communication, 2009, 43: 22-23. |
| [14] |
李芬芬, 宋子荣, 刘军林. 室内分布系统链路预算模型的探讨[J].
移动通信, 2008, 32(11): 63-66.
Li F F, Song Z R, Liu J L. Discussed for link budget model of Indoor distribution system[J]. The Mobile Communication, 2008, 32(11): 63-66. DOI: 10.3969/j.issn.1006-1010.2008.11.015. |
| [15] |
付威, 谭展. TD-LTE室内覆盖建设解决方案研究[J].
移动通信, 2012, 36(16): 17-22.
Fu W, Tan Z. The research of the solution for LTE construction of indoor coverage[J]. The Mobile Communication, 2012, 36(16): 17-22. DOI: 10.3969/j.issn.1006-1010.2012.16.004. |
| [16] |
刘德昌. TD-LTE室内覆盖解决方案[J].
电信工程技术与标准化, 2012, 25(10): 48-52.
Liu D C. Solution for TD-LTE indoor distribution system[J]. Telecom Engineering Technics and Standardization, 2012, 25(10): 48-52. DOI: 10.3969/j.issn.1008-5599.2012.10.011. |
| [17] |
Liu H L, Gu F, Zhang Q. Decomposition of a multiobjective optimization problem into a number of simple multiobjective subproblems[J].
Evol Comput, 2013, 18(3): 450-455.
|
 2015, Vol. 32
2015, Vol. 32