粒子群优化算法[1](Particle Swarm Optimization, PSO)是一种用于对连续非线性函数优化的人工智能优化算法, 是Kennedy和Eberhart受人工生命研究结果的启发[2], 于1995年提出的.作为一种基于群体智能的优化算法, 粒子群优化算法可用于求解各种非线性、不可微和多峰值的复杂优化问题, 并在科学和工程领域, 如:神经网络训练、函数优化、模式分类、模糊系统控制等研究领域广泛应用, 出现了很多的研究成果[3-8].但是粒子群优化算法还存在容易陷入局部极值、后期收敛速度慢、精度较差的缺陷.
近年来, 基于粒子群优化算法的改进算法层出不穷[9-12].从不同角度对粒子群优化算法的改进, 在一定程度上取得了一些效果.但是也存在效果不明显、不符合实际应用、实现困难的一些不足.本文提出的改进粒子群优化算法(Modified Particle Swarm Optimization, MPSO)容易实现、效果明显.主要进行了两方面的改进:一方面, 用粒子群中粒子个体极值的加权平均值替代速度更新式中的粒子个体极值, 并根据粒子群中的粒子浓度自适应地调整加速系数; 另一方面, 通过引用两种非线性递减函数对惯性权重进行调整.这样可以容易地使粒子向最优位置移动的速度更快, 全局寻优的能力更强.
2013年12月4日, 工信部正式向三大运营商发布4G牌照, 中国移动、中国电信和中国联通均获得TD-LTE牌照.随着4G时代的到来, 国内运营商需要修建大量新的基站, 这样基站的优化选址成了一个重要需求.为了用最小的基站建设代价来获得最好的服务质量, 一些学者提议使用自动规划算法来获取最优的设计方案.但是, 基站选址优化需要考虑区域的业务量、覆盖率和成本等问题, 目前的寻优搜索算法并不能很好解决其候选解数量庞大、寻优过程复杂、搜索空间多峰分布等难题.
近几年, 出现了一些基于仿生学算法(如:遗传算法、免疫算法、粒子群算法等)的基站选址优化方案[13-15], 本文将改进后的粒子群优化算法应用于4G网络基站选址优化, 结果表明, 改进后的粒子群优化算法具有更高的收敛速度和全局寻优能力.
1 粒子群优化算法原理粒子群优化算法简称粒子群算法.在一个D维的搜索空间和由n个粒子组成的种群中, 第i个粒子的位置表示为一个D维向量:yi=(yi1, yi2, …, yid, …, yiD)每个个体称为一个粒子, 代表着潜在的解, 这些解的优劣由适应度值函数决定, 适应度值函数与问题的目标函数有关; vi=(vi1, vi2, …, vid, …, viD)为粒子i的速度; pi=(pi1, pi2, …, pid, …, piD)为粒子i迄今为止搜索到的最优位置; pg=(pg1, pg2, …, pgd, …, pgD)为整个粒子群迄今为止搜索到的最优位置; 另设f(yidk)为粒子i在第k次迭代中第d维的目标函数.
由此得出粒子的位置和速度更新公式:
| $ \mathit{\boldsymbol{v}}_{id}^{k + 1} = \omega \mathit{\boldsymbol{v}}_{id}^k + {c_1}\alpha \left( {\mathit{\boldsymbol{p}}_{id}^k - \mathit{\boldsymbol{y}}_{id}^k} \right) + {c_2}\beta \left( {\mathit{\boldsymbol{p}}_{gd}^k - \mathit{\boldsymbol{y}}_{id}^k} \right); $ | (1) |
| $ \mathit{\boldsymbol{y}}_{id}^{k + 1} = \mathit{\boldsymbol{y}}_{id}^k + \mathit{\boldsymbol{v}}_{id}^{k + 1}. $ | (2) |
式中:vidk是粒子i在第k次迭代中第d维的速度; pidk是粒子i在第k次迭代中第d维的最优位置; pgdk为第k次迭代中第d维的全局最优位置; yidk是粒子i在第k次迭代中第d维的位置; α(pidk-yidk)称为第d维的“认知”部分, 而β(pgdk-yidk)称为第d维的“社会”部分, 分别表示粒子本身思考和粒子间的信息共享; c1和c2为常数, 分别表示“认知”和“社会”部分对粒子速度的影响, 可根据算法需要设置不同的值; ω为惯性权重, 其大小决定着局部最优和全局最优能力; α和β是[0, 1]区间内均匀分布的随机数, 用来保持群体多样性.
在粒子群算法不断迭代的初期, 由于pid和pgd不断更新变化, 其全局搜索能力强, 收敛速度快, 而在中后期, pid和pgd变化不大, 此时粒子的速度越来越小, 最后趋近于零, 这样粒子位置得不到更新, 整体上就可能陷入局部最优, 这是粒子群算法的主要缺陷[16].
2 改进的粒子群优化算法本文对粒子群优化算法的改进将从两个方面入手, 以实现改进算法收敛速度和寻优能力的平衡.
2.1 权值模式的粒子群更新算法从式(1)和式(2)可以看出, 基本的粒子群优化算法没有充分利用其他粒子的个体最优位置的信息.为很好地体现所有粒子的个体最优位置的信息, 取第d维的padk为第d维的pidk的加权和, 得到
| $ \mathit{\boldsymbol{p}}_{ad}^k = \sum\limits_{i = 1}^n {{a_{id}}\mathit{\boldsymbol{p}}_{id}^k} , $ |
其中
| $ \mathit{\boldsymbol{v}}_{id}^{k + 1} = \omega \mathit{\boldsymbol{v}}_{id}^k + {c_1}\alpha \left( {\mathit{\boldsymbol{p}}_{ad}^k - \mathit{\boldsymbol{y}}_{id}^k} \right) + {c_2}\beta \left( {\mathit{\boldsymbol{p}}_{gd}^k - \mathit{\boldsymbol{y}}_{id}^k} \right). $ | (3) |
式(3)中, padk表示第d维其他粒子的个体最优位置的信息, 这样本公式充分考虑了所有粒子的个体最优位置信息, 这里将改进后的粒子群优化算法记为MPSO-W(Modified Particle Swarm Optimization-Weight Facter).
2.2 调整ω值的粒子群更新算法在基本粒子群优化算法中, 惯性权重的调整变化对算法的性能有很大影响, 权值ω较大时算法的全局搜索能力强, 相反权值ω较小时算法的局部搜索能力强.为了更加合理地反映粒子群搜索的非线性过程, 本文分别对ω进行调整以构造两种非线性函数.其具体表示分别如下.
| $ \begin{array}{l} \omega = \left( {{\omega _{\max }} - {\omega _{\min }}} \right)\left( {\frac{t}{{\max gen}}} \right) + \left( {{\omega _{\max }} - {\omega _{\min }}} \right) \times \\ {\left( {\frac{t}{{\max gen}}} \right)^2} + \left( {{\omega _{\max }} - {\omega _{\min }}} \right){\left( {\frac{t}{{\max gen}}} \right)^3} + {\omega _{\max }}, \end{array} $ | (4) |
其中:ωmax表示最大的惯性权重; ωmin表示最小的惯性权重; maxgen表示最大迭代次数; t表示当前迭代次数.式(4)是一条开口向上的非线性函数曲线, 这里将其记为MPSO-U(Modified Particle Swarm Optimization-Up).
| $ \omega = {\omega _{\min }}{\left( {\frac{{{\omega _{\max }}}}{{{\omega _{\min }}}}} \right)^{1/\left( {1 + mt/\max gen} \right)}}, $ | (5) |
式(5)是一个非线性指数函数, 这里将其记为MPSO-E(Modified Particle Swarm Optimization-Exponential).由实验得出m=5时, 函数的寻优能力最好, 所以本文取m=5.同时将上述的两种改进后的方法进行结合, 将MPSO-W与MPSO-U结合后记为PSO1, 将MPSO-W与MPSO-E结合后记为PSO2.
2.3 全局收敛性分析与仿真比较在第d维空间中, 设初始条件为yid0=y0, yid1=y1, 由式(4)和(5)得到如下递归关系:
| $ \mathit{\boldsymbol{y}}_{id}^{k + 1} = \left( {1 - \omega {s_1} - {s_2}} \right)\mathit{\boldsymbol{y}}_{id}^k - \omega \mathit{\boldsymbol{y}}_{id}^{k - 1} + {s_1}\mathit{\boldsymbol{p}}_{ad}^k + {s_2}\mathit{\boldsymbol{p}}_{gd}^k, $ | (6) |
式(6)中, s1=c1α, s2=c2β.推导得出式(6)的封闭形式为:yidk=k1d+k2dφk+k3dηk, 由此求出
为了验证改进PSO算法的性能, 本文分别采用Sphere、Griewank、Rastrigrin和Ackley函数进行仿真测试[17], 其中Sphere函数是非线性单峰函数, Griewank、Rastrigrin和Ackley函数是非线性多峰函数, 当它们取到合适的值时, 最优值都是0.下文中, 成功率是指搜索成功次数与总实验次数比值; 最优值是指搜索到的最优值与实际全局最优值的差值; 迭代次数是指平均收敛迭代次数.成功搜索时, 目标函数的最优值应小于预设的精度.
在仿真测试中, 设最大迭代次数为200次, 随机仿真200次; 改进算法的参数设置如下:c1=2, c2=2, ωmax=0.9, ωmin=0.4;初始粒子群随机均匀分布, 取粒子数为30个, 维数为30维; Ackley函数的初始值在[-32, -16]范围内随机均匀分布; 在引入加权值的同时, 分别用上述两种非线性方法对惯性权重ω进行调整, 测试结果如表 1所示.
| 表 1 非线性函数优化测试比较 Table 1 Nonlinear function optimization test comparison |
由表 1结果可以看出, 改进后的粒子群算法对Sphere函数的寻优能力没有多大改善; 对Griewank函数的寻优能力变化不大, 但其收敛速度有所提升; 由于引入了改进机制, PSO1和PSO2算法的寻优精度稍有下降; 但是对于Rastrigrin和Ackley函数, 其寻优性能明显得到改善, 其寻优成功率和收敛速度均显著提高.实验结果可以看出改进后的粒子群算法可应用于非线性多峰函数的优化问题.
3 网络基站选址优化 3.1 网络基站选址模型基站选址优化是通信网络的一个重要内容, 即在考虑建站成本、覆盖率及其他参数的情况下, 用最小的建设成本来获得最大覆盖率的网络, 这也是4G网络基站选址优化的目标.
由于实际地形比较复杂, 为了简化计算, 先将基站优化地区网格进行离散化, 从中选取16个适合部署基站的位置, 再从其中选取8个位置部署基站, 每个基站装配两种型号天线中的一种.这样基站选址优化问题就转化为:在16个可以部署基站的位置中, 寻找到8个位置装配天线, 在考虑成本的前提下, 使得基站覆盖率最大化.对于这样的问题将会存在很多种组合的覆盖率均为最大, 也就是存在很多的局部极值, 目标函数与Rastrigrin和Ackley函数的特性相似, 所以拟采用本文改进后的算法进行基站选址优化.
3.2 基站优化算法设计 3.2.1 变量与参数设置首先, 映射变量:为了使计算更加简单, 利于本文改进算法寻优, 将基站部署的组合优化问题用自然数来映射, 一种组合对应一个自然数序列, 设为sta_pos, 其中选中为1, 没选中为0.对于天线型号设为sta_ant, 采用同样的方法分别记为6和9(6为A型天线, 9为B型天线).这样就将组合优化问题简化为整数寻优问题.然后, 设置参数:设初始粒子群维数为2, 分别为sta_pos和sta_ant, 粒子数设为16个, c1=2, c2=2, ωmax=0.9, ωmin=0.4, 由于模型比较大, 为了获得较短的寻优时间, 最大迭代次数设为200次.
3.2.2 编码方式与目标函数选取基站选址不仅要考虑基站的位置, 还要考虑基站自身的设置.考虑的基站参数有:基站位置、基站高度、发射功率、天线型号和新站旧站共建等.这样基站的信息就可以用一个点来表示, 也就是粒子群里的一个粒子.其编码方式如下:
| $ \sigma = \left[ {\begin{array}{*{20}{c}} {基站位置}\\ {基站高度}\\ {发射功率}\\ {天线型号}\\ {新站旧站} \end{array}} \right]. $ | (7) |
仿真环境:以珠三角地区某市的4G网络基站优化部署作为实验背景.该市4G网络的规划覆盖区域为5 km×5 km; 基站位置为北纬和东经坐标; 基站高度为40~50 m; 基站发射功率为40~50 W; 天线型号有A型和B型; 已有部分旧的2G/3G基站分布数据库.
为了降低4G网络的建站成本, 优先考虑4G与旧的2G或3G站点共站.利用旧站时, 只考虑4G天线的成本, 建站成本目标函数如下:
| $ {f_1}\left( a \right) = h{C_1} + {l_1}{E_1} + {l_2}{E_2}, $ | (8) |
其中, h为新站个数; C1为建设一个新的4G基站的成本; E1和E2分别为采用A型和B型天线的成本; n=l1+l2为待规划区域将使用的A型和B型天线的总个数.
覆盖率决定了4G网络的性能, 因此, 可以转化为覆盖率最大化问题, 本文采用覆盖率损失目标函数, 以将多目标问题转化为单目标问题, 其定义如下:
| $ {f_2}\left( a \right) = {C_2}\left[ {S - \left( {n{\rm{ \mathsf{ π} }}{r^2} - \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{s_{ij}}} } } \right)} \right], $ | (9) |
其中, C2为覆盖盲区的损失系数; S为基站优化区域的总面积; nπr2为覆盖面积的总和, sij为基站i和j的覆盖重叠区的面积.
本文优化目标函数如下:
| $ g\left( a \right) = {\theta _1}{f_1}\left( a \right) + {\theta _2}{f_2}\left( a \right), $ | (10) |
其中, θ1为建站成本的权重系数; θ2为覆盖区域损失的权重系数.
3.3 仿真结果分析为了验证本文改进算法的性能, 将本文改进算法和PSO算法应用于基站优化部署中(PSO算法中不使用已有的2G/3G基站), 并将其中的一组数据进行仿真比较, 在Matlab环境下仿真10次, 得出结果如表 2所示.
| 表 2 本文改进算法 VS PSO算法仿真结果比较 Table 2 Comparison of the improved algorithm and PSO algorithm simulation results |
从表 2中可以看出, 本文改进算法的平均建站成本和覆盖率都优于PSO算法, 这是因为本文改进算法充分考虑了已有2G/3G基站的分布信息, 利用了已有信息和4G基站共同规划建站.减少了新建4G基站的数目和成本, 从而减少了网络建设的代价.本文改进算法的平均收敛代数也明显优于PSO算法, 这说明本文改进算法具有较优的收敛性能, 从运行时间可以看出, 使用本文改进算法耗时稍长, 但其他各项性能有所提高, 总体上, 本文改进算法是有效的.
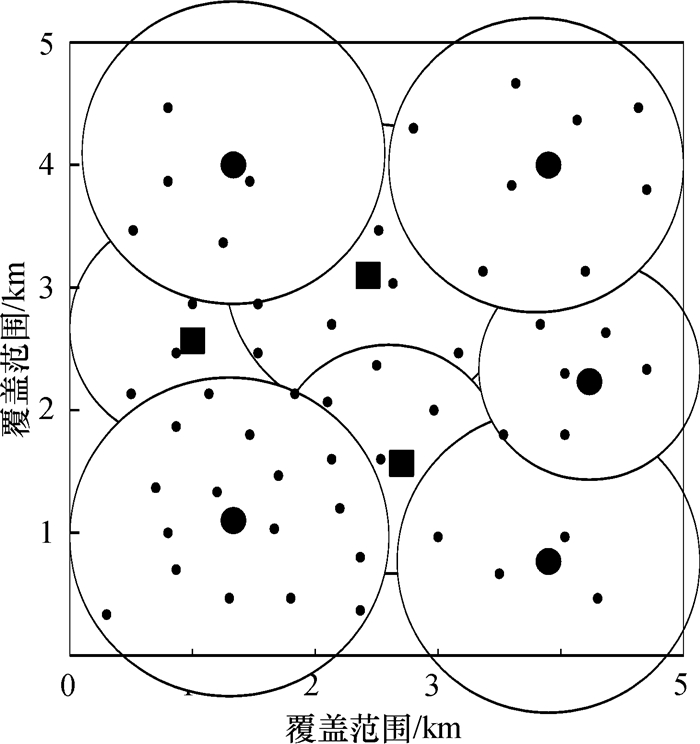
经过多次运行后, 本文改进算法同PSO算法方案的4G网络基站选址结果分别如图 1和图 2所示.图中:星号表示话务热点; 实心方框表示已有的2G/3G网络基站; 实心圆表示新建的4G网络基站; 大小圆圈分别表示A型和B型天线的覆盖范围.从两图的对比可以看出, 本文改进算法方案共选取了3个基站同已有的2G/3G共站, 剩余5个是新建的4G网络基站, 这样一定程度上降低了建站成本.而且, 本文改进算法方案的基站网络热点覆盖率更高, 能够提供较高的网络服务, 赢得更多的客户.
|
图 1 本文改进算法 Figure 1 The improved algorithm |
|
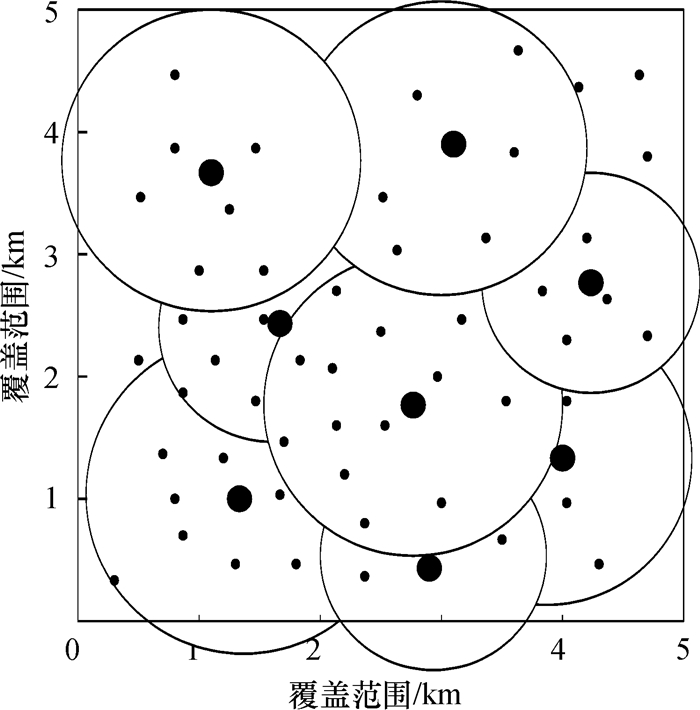
图 2 PSO算法 Figure 2 PSO algorithm |
| [1] |
Kennedy J, Eberhart R C. Particle Swarm Optimization[C]//Proceedings of the IEEE International Conference on Neural Networks. Piscataway: [s. n. ], 1995: 1942-1948.
|
| [2] |
Eberhart R, Kennedy J. A new optimizer using particle swarm theory[C]//Proc of the Sixth International Symposium on Micro Machine an Human Science. Nagoya, Japan: [s. n. ], 1995: 39-43.
|
| [3] |
Clerc M. The swarm and the Queen: Towards a deterministic and adaptive particle swarm optimization[C]// Proc of the Congress of Evolutionary Computation. [S. l. ]: [s. n. ], 1999: 1951-1957.
|
| [4] |
Shi Y, Eberhart R. A modified paticle swarm optimizer[C]//IEEE World Congress on Computational Intelligence. [S. I. ]: [s. n. ], 1998: 69-73.
|
| [5] |
Van den Bergh F, Engebrecht A P. Effects of swarm size on cooperative particle swarm optimizers[C]//Proc of the third Gennetic and Evolutionary computation computation conference. San Francisco, USA: [s. n. ], 2001: 892-899.
|
| [6] |
Lovbjerg M, Rasmussen T K, Krink T. Hybrid particle swarm optimizer with breeding and subpopulations[C]//Proc of the third Gennetic and Evolutionary computation conference. San Francisco, USA: [s. n. ], 2001: 469-476.
|
| [7] |
梁慧. 混沌粒子群优化算法的分析与应用[D]. 广州: 广东工业大学自动化学院, 2011.
|
| [8] |
张磊. 基于分级的粒子群优化算法研究[D]. 广州: 广东工业大学计算机学院, 2011.
|
| [9] |
邢杰, 萧德云. 混合粒子群优化算法及其应用[J].
化工学报(中国), 2008, 59(7): 1707-1710.
Xing J, Xiao D Y. Hybirid particle swarm optimization and its application[J]. Journal of Chemical Industry and Engineering(China), 2008, 59(7): 1707-1710. |
| [10] |
潘勇, 郭晓东. 一种基于遗传算法改进的粒子群优化算法[J].
计算机应用与软件, 2011, 29(9): 222-224.
Pan Y, Guo X D. An improved particle swarm optimisation algorithm based on genetic algorithm[J]. Computer Applicationsand Software, 2011, 29(9): 222-224. |
| [11] |
高鹰, 刘怀亮. 一种改进的粒子群优化算法及其在盲信号分离中的应用[J].
广州大学学报:自然科学版, 2011, 10(6): 42-48.
Gao Y, Liu H L. An improved particle swarm optimizer and its application in blind signals separation[J]. Journal of Guangzhou University:Natural Science Edition, 2011, 10(6): 42-48. |
| [12] |
王娟, 吴宪祥, 郭宝龙. 基于改进粒子群优化算法的移动机器人路径规划[J].
计算机工程与应用, 2012, 48(15): 240-244.
Wang J, Wu X X, Guo B L. Robot path planning using improved particle swarm optimization[J]. Computer Engineering and Applications, 2012, 48(15): 240-244. DOI: 10.3778/j.issn.1002-8331.2012.15.049. |
| [13] |
Munyaneza J, Kurien A. Optimization of antenna placement in 3G nerworks using genetic algorithm[J].
Communications & Information Technology, 2009, 36(5): 70-80.
|
| [14] |
朱思峰, 刘芳, 柴争义. 基于免疫计算的TD-SCDMA网络基站选址优化[J].
通信学报(中国), 2011, 32(1): 106-110.
Zhu S F, Liu F, Chai Z Y. Immune computing-based base station location planning in the TD-SCDMA network[J]. Journal on Communications(China), 2011, 32(1): 106-110. |
| [15] |
闫涛. TD-SCDMA基站选址的免疫优化实现[J].
计算机工程与应用, 2011, 47(31): 206-208.
Yan T. Optimization for location of TD-SCDMA base stations based on immune algorithm[J]. Computer Engineering and Application, 2011, 47(31): 206-208. DOI: 10.3778/j.issn.1002-8331.2011.31.058. |
| [16] |
Yen G G, Leong W F. Dynamic multiple swarm in multiobjective particle swarm optimization[J].
IEEE Trans on Systems, Man, and Cybernetics, Part A: Systems and Humans, 2009, 39(4): 890-911.
DOI: 10.1109/TSMCA.2009.2013915. |
| [17] |
Yao X, Liu Y, Lin G M. Evolutionary Programming Made Faster[J].
IEEE Transactions on Evolutionary Computation, 1999, 3(2): 82-102.
|
 2015, Vol. 32
2015, Vol. 32