离散事件系统是由离散事件按照一定的运行规则相互作用而导致状态演化的一类动态系统.它已经被广泛地应用到计算机集成制造系统、交通运输、军事指挥、计算机网络、柔性生产线以及通讯网络[1].在实际应用中, 可以对事物, 如机械、进程等进行离散化建模得到一个离散事件系统, 但系统运行的某个失误或系统操作的某种不当易使离散事件系统中出现一些故障.因此, 容错离散事件系统从一定意义上来说是更加符合实际的一类离散事件系统.
近年来, 对离散事件系统容错控制的研究引起了国内外的广泛关注.文献[2-15]阐述了离散事件系统对故障事件的处理及其相应模型, 其中文献[2-4]运用错误模式的方法, 把离散事件系统分成多个模式.文献[8]在全可观的情况下, 研究系统的容错性及错误恢复.文献[9-10]研究传感器发生错误时, 控制器如何采取相应的措施—控制器会被转换[9]或重新配置[10].又如, 在自动公路系统(automated highway systems)中, 错误应对模块必须对故障事件实施纠错, 以防止车辆碰撞[11-12].相关的研究还包括文献[13-14], 其中文献[13]研究Petri网的容错性; 文献[14]研究分布式容错控制.文献[15]基于错误矩阵方程, 研究消错学理论.
本文研究离散事件系统的可纠错性, 为离散事件系统的可靠性提供理论支持.在文献[16-17]中, 一个系统是非屏蔽容错(nonmasking fault-tolerant)的当且仅当系统遇到错误后, 系统仍然符合规范.本文正是在文献[16-17]的基础上, 考虑系统在受监控的情况下如何实现它的非屏蔽容错性.事实上, 可纠错性是非屏蔽容错性的必要条件, 即当系统遇到错误后, 可纠错系统可转移到可接受状态.因此, 实现系统的可纠错性是实现系统非屏蔽容错性的重要一步, 对系统避免入侵、保证系统安全有重要意义.
在图论中, 树图可表示根节点到叶子节点的各个路径.类似地, 状态树可表示根节点状态到各叶子状态的各个路径.当一棵状态树的叶子节点全是可接受状态时, 根节点一定能转移到可接受状态, 而这一性质正是可纠错状态的必要条件.在下文可以知道, 状态树可加上约束变为判定树, 判定树能构造出可纠错状态的充要条件.因此, 状态树是描述可纠错状态的可靠模型.本文基于状态树, 给出了可纠错状态的形式化定义, 并证明了可纠错状态一定能转移到可接受状态这一性质.
此外, 本文给出判定可纠错状态的算法, 此算法通过一个状态能构造出的最小递归深度的状态树, 判定该状态的可纠错性, 并且此算法具有多项式时间复杂度.
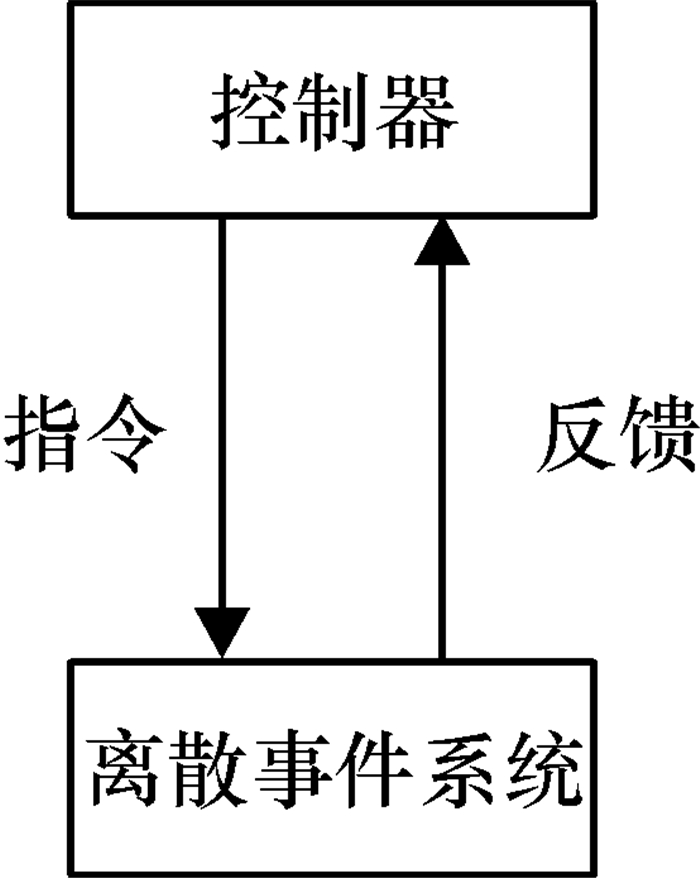
1 离散事件系统可纠错性的非形式讨论首先引入控制器的概念.如图 1所示, 控制器是对离散事件系统传送指令的部件.
|
图 1 控制器功能图 Figure 1 Graph of controller function |
控制器具有以下3种功能:
(1) 强制添加可控事件, 在不可控事件发生之前时, 控制器可启动事件, 对当前状态实施控制.本文假定控制器只能强制添加可控事件.
(2) 使接下来的可控事件不生效(disable).
(3) 终止系统.当系统出现严重错误时, 控制器终止系统.
规定控制器具有上述3个功能是合理的, 比如, 通常的电灯开关系统可以视为一个控制器, 事件“开”和“关”都是可控的, 如果想电灯由关变为开, 则可添加事件(也就是拨动开关)“开”; 如果想让电灯保持开状态, 则可禁止(也就是不让其生效)事件“关”发生.如果事件“开”发生, 电灯仍保持关状态(电灯可能损坏了), 则可令系统终止.
在实际应用中, 离散事件系统的运行有时会出现故障, 这些故障称为故障事件.当故障事件发生后, 系统停留在不可接受状态, 此时控制器传送指令, 对系统实施控制, 使得系统重新停留在可接受状态, 这一过程称作纠错.
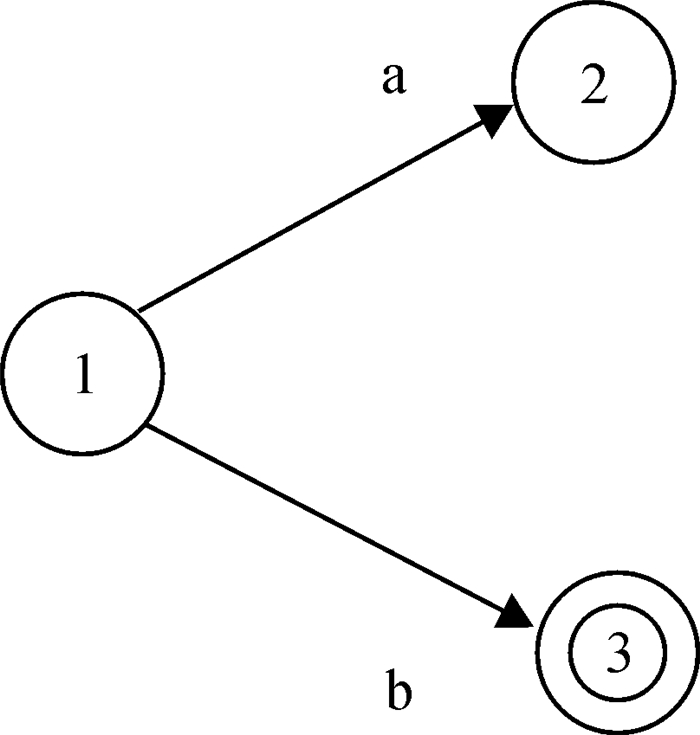
例1:设自动机如图 2所示, 并设事件a是不可控的, 事件b是可控的.当系统停留在状态1时, 控制器可强制添加可控事件b, 使得系统停留在可接受状态3.因此, 当系统停留在状态1时, 控制器可实行纠错.
|
图 2 一个简单的自动机图 Figure 2 Graph of a simple automata |
例2:在例1中, 重新假设事件a是可控的, 事件b是不可控的.当系统停留在状态1时, 如果事件a发生, 那么控制器可使事件a不生效, 系统仍然停留在状态1, 而事件b发生, 系统停留在可接受状态3.因此, 当系统停留在状态1时, 控制器可使系统不能转移到状态2, 从而当系统发生状态转移时, 系统一定是转移到可接受状态3.综上所述, 当系统停留在状态1时, 控制器可实行纠错.
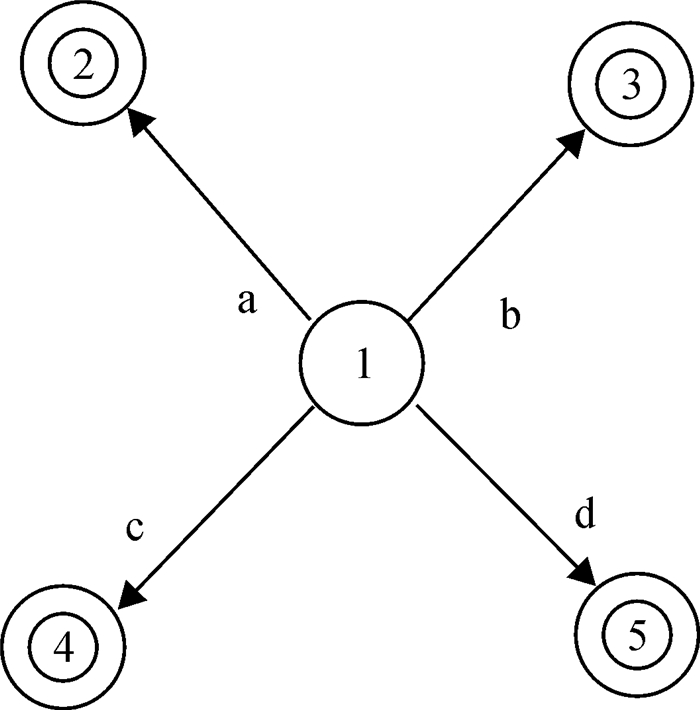
例3:设自动机如图 3所示, 并设所有事件都是不可控事件, 当系统停留在状态1时, 系统是可纠错的.理由如下:系统在状态1发生任何状态转移, 系统都会停留在可接受状态.因此, 在这种情况下, 控制器不实行任何纠错行动, 系统依然是可纠错的.
|
图 3 不带可控事件的自动机图 Figure 3 Graph of an automata without controllable events |
综合上述情况, 可以对离散事件系统的可纠错性形式化.
定义1 (离散事件系统):离散事件系统是一个5元组:
| $ G: = \left( {Q, \Sigma, \delta, {q_0}, {Q_{\rm{a}}}} \right), $ |
其中, Q为状态集, Σ为事件集, δ:Q×Σ→Q为转移函数, q0为起始状态, Qa为可接受状态集且Qa⊆Q.
状态集分为可接受状态集和不可接受状态集, 不可接受状态集记为Qua, Qua=Q-Qa.事件集分为可控事件集和不可控事件集, 可控事件集记为Σc, 不可控事件集记为Σuc, Σuc=Σ-Σc.令Σ*为事件集Σ的kleene闭包, 令ε表示空字符串, 对于任意的q∈ Q, 有δ(q, ε)=q.对于给定的q∈ Q, σ∈Σ, 如果δ(q, σ)未定义, 则记为δ (q, σ)
定义2 (邻域):设一个状态q∈ Q, 则集合{p∈ Q |∃a∈Σ(δ(q, a)=p)}称为q的邻域, 记q的邻域为N(q).集合
| $ \{ p \in {\rm{ }}Q{\rm{ }}|\exists a \in {\Sigma _{\rm{c}}}(\delta \left( {q, a} \right) = p)\} $ |
称为q的可控邻域, q的可控邻域为Nc(q).集{p∈ Q |∃a∈Σuc(δ(q, a)=p)}称为q的不可控邻域, 记q的不可控邻域为Nuc(q).
显然, 对于任意q∈Q, Nuc(q)⊆N(q), Nc(q)⊆N(q).
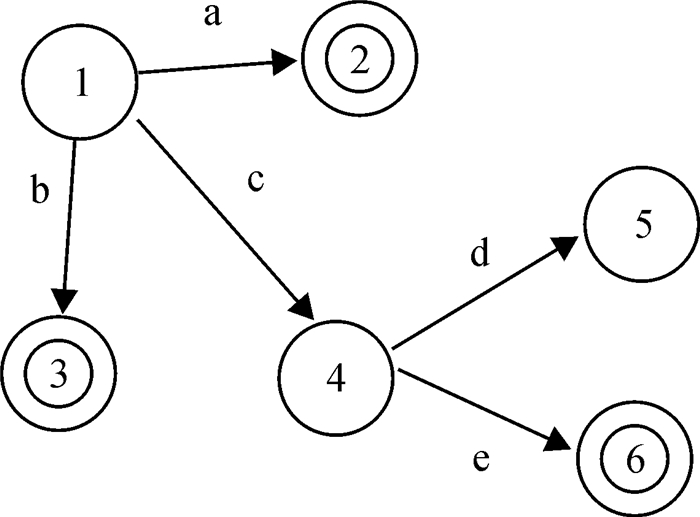
例4:设自动机如图 4所示, 状态1的邻域N(1)是状态集{2, 3, 4}, 状态4的邻域N(4)是状态集{5, 6}, 其余状态的邻域为空集.进一步设事件a和d是可控事件, 其余事件为不可控事件, 那么状态1的可控邻域Nc(1)={2}, 不可控邻域Nuc(1)={3, 4};状态4的可控邻域Nc(4)={5}, 不可控邻域Nuc(4)={6}.
|
图 4 邻域示例图 Figure 4 Graph of neighbor |
定义3 (状态树):设状态树的集合为T, 一个状态树t∈T是一个递归二元组:
| $ t: = ({n_{\rm{r}}}, R({n_{\rm{r}}})). $ |
其中nr∈ Q是t的根节点, R(nr)是二元关系, R(nr)⊆{nr}×T.
定义4 (子树):设t=(nr, R(nr))∈T是状态树, t的子树集为Ts(t), Ts(t)⊆T.
(1) t是t本身的子树, 即t∈Ts(t).
(2) 如果对于任意状态树t′∈T, (nr, t′)∈ R(nr), 则称t′是t的直系子树.如果t′是t的直系子树, 则t′∈Ts(t).记t的直系子树集为Tdl(t).
(3) 对于任意状态树t1t2…tn, 如果对于任意正整数k(1 < k≤n), tk∈Tdl(tk-1), 则tn∈Ts(t1).
定义5 (节点):设t=(nr, R(nr))∈T是状态树, 记t的节点集为ns(t), ns(t)⊆Q.
(1) t的根节点nr是t的节点.即nr∈ns(t).
(2) 对于任意状态树
| $ t = (n',R({{n'}_{\rm{r}}})) \in T, $ |
如果t′∈Ts(t), 则n′r∈ns(t).
设状态树t∈T, t的直系子树的根节点称为t的直系节点, 记t的直系节点集为ndl(t).
在不发生混淆的情况下, 本文用状态树的所有节点来表示状态树.
定义6 (叶子):设
| $ t = \left( {{n_{\rm{r}}}, R\left( {{n_{\rm{r}}}} \right)} \right), t\prime = \left( {{{n'}_{\rm{r}}}, R\left( {n{\prime _{\rm{r}}}} \right)} \right) \in T $ |
是状态树, 如果t′是t的子树且R(nr′) =φ, 其中φ表示空集, 则称t′是t的叶子.
注意, 叶子本质上是状态树(只有一个节点的状态树).在不发生混淆的情况下, 叶子既可看作节点, 也可看作状态树.当叶子被看作节点时, 称叶子为叶子节点.
定义7 (递归深度):设t=(nr, R(nr))∈T是状态树, 记t的递归深度为D(t), D(t)∈
| $ D\left( t \right) = {\rm{max}}\{ D\left( {t\prime } \right) + 1|\left( {{n_{\rm{r}}}, t\prime } \right) \in R({n_{\rm{r}}})\}, $ |
如果D(t)是有限的, 则称t是有限状态树.
定义8 (判定树):设t=(nr, R(nr))∈T是状态树, 对于t的任意子树
| $ t^\prime = \left( {n{ _{\rm{r}}^\prime}, R\left( {n{ _{\rm{r}}^\prime}} \right)} \right) \in {T_{\rm{s}}}(t), $ |
如果t′满足
| $ {n_{{\rm{dl}}}}\left( {t^\prime } \right) = \left( {{N_{{\rm{uc}}}}\left( {n{ _{\rm{r}}^\prime}} \right)} \right) \vee \left( {{n_{{\rm{dl}}}}\left( {t^\prime } \right) \subseteq {N_{\rm{c}}}\left( {n{ _{\rm{r}}^\prime}} \right)} \right), $ | (1) |
则称t是判定树.
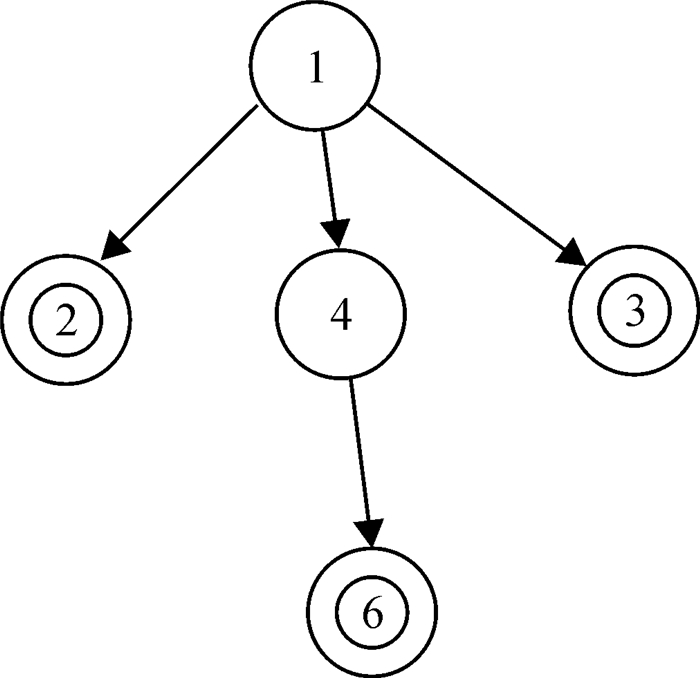
例5:在例4中, 进一步设可接受状态集为{2, 3, 6}, 其余状态为不可接受状态, 事件e是可控事件, 其余事件是不可控事件.考虑图 5的状态树t={1, 2, 3, 4, 6}:
|
图 5 判定树示例图 Figure 5 Graph of decision tree |
状态树t有5棵子树, 分别是{1, 2, 3, 4, 6}、{2}、{3}、{6}和{4, 6}.树{1, 2, 3, 4, 6}的根节点是状态1, 而状态1的不可控邻域等于其直系节点, 即ndl(1)=Nuc(1), 因此树{1, 2, 3, 4, 6}符合定义8的式(1).而ndl(2)=φ⊆Nc(2), 其中φ表示空集, 因此树{2}也符合定义8的式(1), 同理, 树{3}和树{6}符合式(1), 对于树{4, 6}, ndl(4)={6}⊆Nc(6), 符合式(1).根据定义8, 状态树t是判定树.
定义9 (可纠错状态):设离散事件系统G=(Q, Σ, δ, q0, Qa), 状态q∈ Q, 如果存在以q为根节点的有限判定树t=(q, R(q)), 使得t的所有叶子节点都是可接受状态, 则q是可纠错状态; 记可纠错状态集为I.
简单来说, 如果一个状态q∈ Q的可控邻域存在可纠错状态, 则q是可纠错状态, 如果q的不可控邻域的元素全是可纠错状态, 则q也是可纠错状态.
例6:在例5中, 树t={1, 2, 3, 4, 6}是判定树, 根节点是状态1, 且树t的叶子节点全是可接受状态, 因此状态1是可纠错状态.
定理1 如果一个状态q∈ Q 是可纠错的, 则存在事件串s∈Σ*, 使得
| $ \delta \left( {q, s} \right) \in {\rm{ }}{Q_{\rm{a}}}. $ |
证 如果q是可纠错状态, 根据定义9, 存在以q为根节点的有限判定树t, 使得t的所有叶子节点全是可接受状态.对递归深度D(t)作归纳证明:
基础步:设D(t)=0, 则t是叶子, 且叶子的根节点q∈ Qa, 显然δ(q, ε)∈ Qa, 所以∃s∈Σ*(δ(q, s)∈ Qa).定理成立.
归纳步:设D(t)=k, 因为t是判定树, 且根据定义4, t是t本身的子树, q是t的根节点.根据定义8推出:
(ndl(t)=Nuc(q))∨(ndl(t)⊆Nc(q)), 再推出
ndl(t)⊆N(q), 再推出
∀q′∈ndl(t)∃a∈Σ(δ(q, a)=q′).根据定义7可推出
∀(q′, R(q′))∈Tdl(t)(D(q′, R(q′)) < D(t)=k), 再根据归纳假设推出
∀q′∈ndl∃s∈Σ*(δ(q, s)∈Qa), 结合以上式子推出
∀q′∈ndl(t)∃a∈Σ∃s∈Σ*(δ(q, a)=
q′∧δ(q′, s)∈Qa), 再推出
∃s∈Σ*(δ(q, s)∈ Qa), 定理成立.
综上所述, 如果一个状态q∈Q是可纠错的, 则∃s∈Σ*(δ(q, s)∈ Qa).证明完毕.
定理1对可纠错模型有着重要意义, 它表明:如果一个状态是可纠错的, 则此状态能转移到可接受状态.在现实应用中, 一个控制规范K往往是由能转移到可接受状态的字符串组成的, 因此可纠错性往往是可控性的充分条件.
3 可纠错状态的判定算法算法1(判定可纠错状态):
(1) 创建一个初始为空的状态集合A, A称作待判定状态集, 再创建一个初始为空的状态集B, B称作当前可纠错状态集.
(2)把所有可接受状态加入到状态集B中, 把所有不可接受状态加入到状态集A中.如果状态集B为空, 则跳到第5步.
(3) 如果状态集A为空, 则跳到第5步.否则, 从A中取出第1个状态q1, 判定q1:如果∃e∈Σc(δ(q1, e)∈B), 则把状态q1加入到状态集B中, 从A中删除状态q1, 重新开始第3步.否则, 从A中取出第2个状态q2, 用上述方法判定q2, 如此类推, 直到从A中取出最后1个状态qn, 并判定qn.
(4) 从A中取出第1个状态q1, 判定q1:如果Nuc(q1)⊆B, 则把状态q1加入到状态集B中, 从A中删除状态q1, 跳到第3步.否则, 从A中取出第2个状态q2, 用上述方法判定q2, 如此类推, 直到从A中取出最后一个状态qn, 并判定qn.
(5) 把状态集A设定为不可纠错状态集, 状态集B设定为可纠错状态集.
算法结束.
算法1中, 程序每跳到第3步一次, 则称作一次迭代.从算法1中可得以下性质:
性质1 全部状态的可纠错性只需m次迭代即可得到判定, 其中m≤|Q|.
因为在一次迭代中, 如果此次迭代不是最后一次迭代, 则有且只有一个状态的纠错性得到判定, 而状态数目为|Q|, 因此迭代次数小于等于|Q|.
性质2 第k次迭代最多需进行|δ|-k+1次比较, 其中|δ|表示转移函数(作为一个集合)的基数.一般地, 0≤|δ|≤|Q|×|Σ|, 其中|Q|、|Σ|分别表示状态数和事件数.
结合性质1、2, 可得算法的时间复杂度.
性质3 算法1的时间复杂度是Ο(|δ|3)的.
4 结论在故障可诊断但不可控的前提下, 本文研究了离散事件系统基于状态树的可纠错性, 给出了可纠错性的形式化定义, 使得可纠错模型符合现实应用中的规范.同时给出了判定可纠错状态的算法, 使得算法具有多项式时间复杂度.
| [1] |
Cassandras C G, Lafortune S. Introduction to discrete event systems[M]. New York: Springer, 2008: 145-148.
|
| [2] |
Shu S, Lin F. Fault-tolerant control for safety of discrete-event systems[J].
IEEE Transactions on Automation Science & Engineering, 2014, 11(1): 78-89.
|
| [3] |
Shu S, Lin F. Fault-tolerant control for safety of discrete event systems[C]//12th International Conference on Control Automation Robotics & Vision(ICARCV), 2012: 276-281.
|
| [4] |
Shu S, Zong W. Recoverability of faulty discrete event systems[C]//12th International Conference on Control Automation Robotics & Vision(ICARCV), 2012: 258-263.
|
| [5] |
Rohloff K R. Sensor failure tolerant supervisory control[C]//44th IEEE Conference on Decision and Control and 2005 European Control Conference. CDC-ECC'05, 2005: 3493-3498.
|
| [6] |
Wen Q, Kumar R, Huang J, et al. Weakly fault-tolerant supervisory control of discrete event systems[C]//2007 IEEE American Control Conference(ACC'07), 2007: 5649-5654.
|
| [7] |
Wen Q, Kumar R, Huang J, et al. Fault-tolerant supervisory control of discrete event systems: Formulation and existence results[C]//Dependable Control of Discrete Systems. 2007, 1(1): 175-180.
|
| [8] |
Wen Q, Kumar R, Huang J, et al. A framework for fault-tolerant control of discrete event systems[J].
IEEE Transactions on Automatic Control, 2008, 53(8): 1839-1849.
DOI: 10.1109/TAC.2008.929388. |
| [9] |
Darabi H, Jafari M A, Buczak A L. A control switching theory for supervisory control of discrete event systems[J].
Robotics and Automation, IEEE Transactions on, 2003, 19(1): 131-137.
DOI: 10.1109/TRA.2002.807551. |
| [10] |
Rohloff K R. Sensor failure tolerant supervisory control[C]//Decision and Control, 2005 and 2005 European Control Conference. CDC-ECC'05. 44th IEEE Conference on. IEEE, 2005: 3493-3498.
|
| [11] |
Lygeros J, Godbole D N, Broucke M. A fault tolerant control architecture for automated highway systems[J].
Control Systems Technology, IEEE Transactions on, 2000, 8(2): 205-219.
DOI: 10.1109/87.826792. |
| [12] |
Godbole D N, Lygeros J, Singh E, et al. Communication protocols for a fault-tolerant automated highway system[J].
Control Systems Technology, IEEE Transactions on, 2000, 8(5): 787-800.
DOI: 10.1109/87.865852. |
| [13] |
Iordache M V, Antsaklis P J. Resilience to failures and reconfigurations in the supervision based on place invariants[C]//Proceedings of the 2004 American Control Conference. 2004: 4477-4482.
|
| [14] |
Takai S, Ushio T. Reliable decentralized supervisory control of discrete event systems[J].
Systems, Man, and Cybernetics, Part B:Cybernetics, IEEE Transactions on, 2000, 30(5): 661-667.
DOI: 10.1109/3477.875443. |
| [15] |
闵惜琳, 黄甲松, 戚建新, 等. 基于错误矩阵方程的消避错专家系统[J].
广东工业大学, 2012, 29(2): 21-27.
Min X L, Huang J S, Qi J X, et al. Expert system for error eliminating and avoiding based on error matrix equation[J]. Journal of Guangdong University of Technology, 2012, 29(2): 21-27. |
| [16] |
Arora A, Kulkarni S S. Component based design of multitolerant systems[J].
Software Engineering, IEEE Transactions on, 1998, 24(1): 63-78.
DOI: 10.1109/32.663998. |
| [17] |
Attie P C, Arora A, Emerson E A. Synthesis of fault-tolerant concurrent programs[J].
ACM Transactions on Programming Languages and Systems(TOPLAS), 2004, 26(1): 125-185.
DOI: 10.1145/963778. |
 2015, Vol. 32
2015, Vol. 32

