搬运介质、搬运方式、沉积环境和气候等控制因素, 在某种程度上对沉积物粒度参数会产生影响, 沉积环境与粒度组分的形成和搬运也具有非常密切的关系[1-3].在现代沉积学及古代沉积物的沉积环境研究中, 利用分析处理粒度数据是准确判断沉积环境的一种兼具理论价值和现实意义的重要方法.
相关研究中, 萨胡[4]在碎屑沉积物研究中, 利用数学判别分析方法对不同成因的样品进行分析研究, 得出4类沉积环境间的判别函数; 曲政[5]给出了粒度母体分解图, 其可以用于表征单样品的粒度分布; 薛清太[6]通过测试分析发现, 影响油藏岩石渗透能力的重要因素与沉积岩粒度中值分布、泥质含量、分选性等有关, 而混合正态分布可以较好地描述低渗透砂岩油藏中沉积物的粒度分布特征; 杨锐[7]则利用数理统计方法, 对相应的粒度参数运用无偏估计, 相较于以往参数估计, 得到了更加符合无系统误差的评选标准, 并将其应用到了长乐东部海岸的风沙研究当中, 对此环境的风沙进行了系统的粒度参数分析; 张平、宋春晖[8]定量化分析了典型稳定湖相沉积物以及典型风成黄土的粒度参数, 然后利用Fisher准则, 分别建立了湖相判别函数与风成沉积物判别函数.
在上述研究的基础上, 本文拟将判别分析理论应用于沉积环境的综合评判中, 利用模糊理论和神经网络技术各自的优势, 建立模糊神经网络模型, 对实际的潮汐水道等沉积环境进行判别, 并通过实验验证其判别准确率.
1 模糊神经网络模糊神经网络[9-10](Fuzzy Neural Network, FNN)本质上就是神经网络(Neural Network, NN)的模糊化, 即将NN的输入值、权值模糊化, 这种网络结合了模糊逻辑与NN的优点, 既可以具有模糊逻辑的不确定信息处理能力, 又可以有NN的自学习能力, 因此在控制领域有很广泛的应用前景.当前, 常见的模糊神经网络类型如下:
(1) FNN1:输入值为实数, 权值为模糊量;
(2) FNN2:输入值为模糊量, 权值为实数;
(3) FNN3:输入值和权值均为模糊量.
本文将采用FNN2型模糊神经网络.
2 沉积环境判别理论 2.1 相关概念根据《沉积岩石学》第3版[1]中的定义, 沉积环境主要是指:海、陆、河、湖、沼泽、冰川、沙漠等分布及其地势的高低, 而碎屑颗粒是碎屑岩的主要组成部分, 粒度是碎屑颗粒的主要结构特征, 而粒度即为碎屑颗粒的绝对大小, 通常用颗粒直径表示.碎屑颗粒的大小是碎屑岩分类命名的重要依据, 因为它直接决定岩石的类型和性质.
粒度分析的两大主要目标包括对碎屑岩的粒度大小和粒度分布的研究, 其中碎屑岩的粒度分布及其分选性不仅是沉积介质能量大小的衡量指标, 也是判别沉积时衡量自然地理环境和水动力条件的一个良好标志.粒度分析不仅在研究沉积水动力条件和沉积储层评价等方面意义重大, 而且在气候变化和环境演变等研究领域也得到广泛的应用.
2.2 粒度参数选取粒度研究主要以平均粒径、中值、标准偏差、分选、峰度和偏度等常见的粒度参数为主.这些粒度参数及其组合特征不仅可以代表碎屑物质的粒度特征, 而且是衡量沉积环境及其水动力条件的重要参考指标.目前大多数研究所涉及的粒度参数均采用福克和沃德定义.本文所选取的粒度参数如下:
(1) 平均粒径, 表示粒度分布的集中趋势:
| $ {M_z} = \frac{{{\varphi _{16}} + {\varphi _{50}} + {\varphi _{84}}}}{3}. $ |
(2) 标准偏差, 表示颗粒大小的均匀程度:
| $ {\sigma _1} = \frac{{{\varphi _{84}}-{\varphi _{16}}}}{4} + \frac{{{\varphi _{95}}-{\varphi _5}}}{{6.6}}. $ |
(3) 偏度, 用于判别粒度分布的不对称程度:
| $ S{K_1} = \frac{{{\varphi _{16}} + {\varphi _{84}}-2{\varphi _{50}}}}{{2\left( {{\varphi _{84}}-{\varphi _{16}}} \right)}} + \frac{{{\varphi _5} + {\varphi _{95}}-2{\varphi _{50}}}}{{2\left( {{\varphi _{95}} - {\varphi _5}} \right)}}. $ |
(4) 峰度, 用于衡量粒度频率曲线的尖锐程度:
| $ {K_G} = \frac{{{\varphi _{95}}-{\varphi _5}}}{{2.44\left( {{\varphi _{75}}-{\varphi _{25}}} \right)}}. $ |
碎屑岩的粒度与沉积环境、搬运介质及搬运方法等关系密切:一方面前者受后者的影响, 反过来, 后者的特性也必然会反映在前者的相应性质当中, 这也正是应用粒度资料来确定沉积环境的重要依据.运用比较合理的方法, 对不同粒度组成成分进行分析, 一般选择相关的粒度参数作为判断依据, 建立起沉积环境判别与分类的模糊神经网络模型, 并将相关粒度参数应用于所建立的模型当中, 以判别出各自相应的沉积环境.
3 BP模糊神经网络模型 3.1 输入数据标准化由于粒度参数间大小相差比较大, 因而需要对其进行数值标准化.所采用的公式为:
| $ y = \frac{{x-{x_{{\rm{min}}}}}}{{{x_{{\rm{max}}}}-{x_{{\rm{min}}}}}}, $ |
其中, x表示输入数据, xmin表示输入数据的最小值, xmax表示输入数据的最大值, y表示标准化后的数据.
3.2 输入数据模糊化和输出数据去模糊化在既定的模糊规则的基础上, 为了使数据表达形式更加接近实际, 也为了得到新的模糊规则, 一种可行的方法是将无法通过明确隶属关系表示的量化值在数据空间中进行重新划分[11], 这也是数据模糊化的首要目标.模糊化主要通过隶属度函数实现, 本文模糊化处理采用梯形隶属度函数进行计算, 计算公式为[12-13]:
| $ \mu \left( x \right) = \left\{ {\begin{array}{*{20}{l}} {\;\;\;\;\;0}&{\;\;\;\;\;x \le a - c,}\\ {\frac{{c + x - a}}{{c - b}}}&{a - c < x \le a - b,}\\ {\;\;\;\;\;1}&{a - b < x \le a + b,}\\ {\frac{{c - x + a}}{{c - b}}}&{a + b < x \le a + c,}\\ {\;\;\;\;\;\;0}&{\;\;\;\;x > a + c.} \end{array}} \right. $ |
式中, x表示输入知识的量化值; a、b、c表示划分模糊子集的变量区间临界值.本文将采用单点模糊集法和最大隶属度原则对输出知识的反模糊化规则进行分析[14-15].计算规则为当输出值大于0.8时, 其去模糊化值为1, 小于0.8时取0.类别空间则划分为一个二维向量:{1, 0}和{0, 1}.
3.3 神经网络相关优化本模型中对于网络的学习率和误差函数进行了一定的优化, 使得本网络的收敛性能、学习速度得到提升, 误差表征更具有说服力.
(1) 学习率.
通常网络算法中的学习率α是固定的, 但为提高收敛速度和学习速度, 可以根据实际情况选择适合的α(0 < α < 1), 本文选用自适应调整的学习率[16]:
若e增大, 则本次网络总误差调整无效, 且:
| $ \alpha = {\mu _1}\alpha \;\;\;\;\;\;\;0 < {\mu _1} < 1; $ |
若e减小, 则有效, 且:
| $ \alpha = {\mu _2}\alpha \;\;\;\;\;{\mu _2} > 1. $ |
其中, α为神经网络的学习率, μ1、μ2为调节因子,
(2) 附加动量项.
传统BP神经网络算法在训练过程中, 很容易陷入局部极小值, 从而导致震荡, 使收敛放慢.为避免这一问题, 同时又使得训练速度得到提高, 借鉴文献[17-18]的方法, 本文在权值调整公式中引入附加动量项:
| $ \Delta {w_i}\left( k \right) =-\alpha \frac{{\partial e}}{{\partial {w_i}}} + mf\Delta {w_i}\left( {k-1} \right), $ |
其中, Δwi为神经网络权值, mf为动量因子, 其可以反映出之前积累的调整经验.当误差梯度出现局部极小时, 即使
仿真实验环境为:操作系统为Windows 7 Ultimate, 处理器为Intel T6400, 内存为2GB, 仿真软件为Matlab 7.8a.如图 1所示.沉积环境判别的模糊神经网络模型结构分为5层, 主要包括输入层、模糊化层、非线性映射层、结果层、反模糊化层等5部分.该模型是一个多输入单输出的FNN2型BP模糊神经网络模型, 其中n表示输入单元和隐单元个数; X1, X2, …, Xn为n个评价指标的量化值; R1, R2, …, Rn为评价指标经隶属度函数量化后的隶属度向量, 而Rn=(Rn1, Rn2, …, Rnn), wij, wjk分别表示输入层到隐层, 隐层到结果层的连接权值; y′为样本X1, X2, …, Xn的网络输出, y为反模糊化y′后的结果.
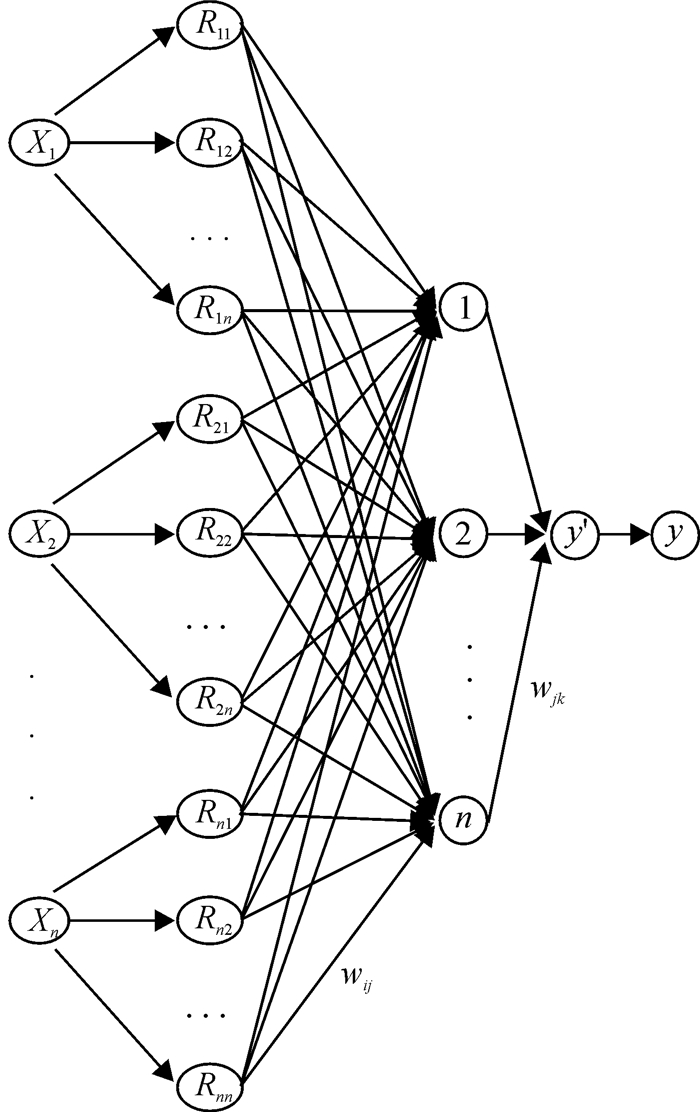
|
图 1 FNN2型BP模糊神经网络结构图 Figure 1 BPFNN2 Structure Diagram |
根据之前对珠江口盆地某凹陷的研究, 笔者在划分该凹陷某一区域的沉积微相期间进行了大量的粒度实验, 从而得到了一系列与沉积微相对应的粒度数据.本文中, 所使用的沉积环境样本数据总共有53个, 每个样本均包含有2.2节所定义的4个粒度参数, 随机将其中的42个样本作为网络的训练样本, 则剩下的11个作为测试样本.沉积环境类别有两类, 分别为潮汐水道(Ⅰ)和水下分流河道(Ⅱ), 如表 1所示.
| 表 1 沉积环境部分训练样本(左)和待测试样本(右) Table 1 A part of sedimentary environment training samples (left) and the testing samples (right) |
模糊神经网络沉积环境判别的计算过程如下:
(1) 输入沉积环境训练样本、沉积环境种类、待预测样本各项指标的数量化值;
(2) 按照3.2节所描述的隶属度函数, 将(1)中的输入全部模糊化;
(3) 调用模糊隶属函数以获取模糊输入样本和模糊目标样本;
(4) 利用本文所设计的网络对模糊输入样本进行训练, 当训练目标误差达到期望后计算收敛, 得到结果样本;
(5) 反模糊化所得到的结果样本, 得到判别结果.
为体现所设计模型的优越性, 本文也将利用MATLAB自带的神经网络工具箱, 将其中常规的BP神经网络算法对同样的沉积数据进行训练和测试, 对比的结果与分析将在后文中展示.
4.3 结果对比与评价分类正确率Ratio用以下公式进行计算:
| $ {\rm{Ratio}} = \frac{{{\rm{Cid}}}}{{{\rm{Cid\_old}}}} \times 100\% . $ |
其中, Cid表示测试样本被分类正确的数据个数, Cid_old表示测试样本本身所提供的相应的沉积环境样本个数.测试样本沉积环境判别的正确率将以表格的形式给出.如表 2、3所示.
| 表 2 BP神经网络判别结果 Table 2 The discriminant result of BPNN |
| 表 3 改进的BP模糊神经网络判别结果 Table 3 The discriminant result of improved BPNN |
基于MATLAB实现的模糊神经网络判别模型经过学习训练, 收敛速度更快(见图 2), 网络训练误差最大仅为0.83%, 说明所建立的模型性能良好, 计算精度高.表 2、3表明, 本文所建立的模型相较于MATLAB工具箱中的BP神经网络模型, 误判率明显低于后者, 验证了本网络模型的学习性、稳定性以及泛化性.
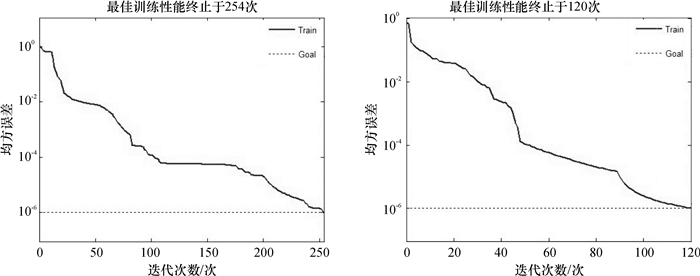
|
图 2 BP神经网络(左)与改进的BP模糊神经网络(右)收敛速度 Figure 2 The convergence rate of BPNN(left) and improved BPNN(right) |
沉积环境判别分类问题是一个较为复杂的模糊性非线性问题.本文将模糊理论与神经网络相关算法结合起来, 建立的模糊神经网络模型对沉积环境进行判别, 检验结果表明碎屑岩的沉积环境能够得到比较准确的判别, 因而本文的模型具有良好的学习性、稳定性和推理性且网络结构清晰, 结果客观合理, 工程实用价值较高, 易于推广.
| [1] |
董文娟, 朱远鑫, 万明刚. 基于Fisher判别准则的沉积环境判别与分类方法[J].
长江大学学报:自然科学版, 2011, 8(5): 5-7.
Dong W J, Zhu Y X, Wan M G. Identification and classification of sedimentary environment based on fisher discriminant analysis[J]. Journal of Yangtze University:Nat Sci Edit, 2011, 8(5): 5-7. |
| [2] |
董文娟, 朱远鑫, 万明刚, 等. 沉积环境判别与分类的Bayes判别分析法[J].
成都大学学报:自然科学版, 2011, 30(2): 139-141.
Dong W J, Zhu Y X, Wan M G, et al. Sedimentary environment discriminant and classified bayes discriminant analysis[J]. Journal of Chengdu University:Natural Science Edition, 2011, 30(2): 139-141. |
| [3] |
李开封, 穆桂金, 徐立帅, 等. 塔里木河干流古河道表层沉积物粒度特征及其意义[J].
水土保持通报, 2012, 32(1): 161-164.
Li K F, Mu G J, Xu L S, et al. Grain size characteristics and their significance for surface sediment of paleochannels along main stream of tarim river[J]. Bulletin of Soil and Water Conservation, 2012, 32(1): 161-164. |
| [4] |
赵澄林, 朱筱敏.
沉积岩石学[M]. 第三版. 北京: 石油工业出版社, 2001.
|
| [5] |
曲政. 沉积物粒度数据表征方法的研究[J].
中国粉体技术, 2001, 7(4): 24-31.
Qu Z. Research on sediment grain size data characterization methods[J]. China Powder Science and Technology, 2001, 7(4): 24-31. |
| [6] |
薛清太. 低渗透砂岩油藏沉积物粒度分布特征研究[J].
沉积学报, 2006, 24(3): 414-418.
Xue Q T. Investigation on Characteristics of Granulometric Distribution of Sediments in Low-penmeability Sandstone Reservoir[J]. Acta Sedimentologica Sinica, 2006, 24(3): 414-418. |
| [7] |
杨锐, 雷怀彦, 刘建辉, 等. 沉积物粒度参数的无偏估计及其在长乐海岸的应用[J].
海洋地质动态, 2007, 23(10): 33-36.
Yang R, Lei H Y, Liu J H, et al. No partial estimate of sedimentary grain size parameters and its application in Changle Coast[J]. Marine Geology Letters, 2007, 23(10): 33-36. DOI: 10.3969/j.issn.1009-2722.2007.10.009. |
| [8] |
张平, 宋春晖. 稳定湖相沉积物和风成黄土粒度判别函数的建立及其意义[J].
沉积学报, 2008, 26(3): 501-507.
Zhang P, Song C H. The significance and establishment of discriminant function with grain size of stable lacustrine sediment and eolian loess[J]. Acta Sedimentologica Sinica, 2008, 26(3): 501-507. |
| [9] |
宋彬彬. 模糊神经网络的发展与应用[J].
煤炭技术, 2012, 31(007): 198-199.
Song B B. Development and Application of fuzzy neural network[J]. Coal Technology, 2012, 31(007): 198-199. |
| [10] |
刘伟, 蔡前凤. 决策模型的神经网络表示[J].
广东工业大学学报, 2007, 24(03): 24-27.
Liu W, Cai Q F. Neural networks representation of decision models[J]. Journal of Guangdong University of Technology, 2007, 24(03): 24-27. |
| [11] |
张吉礼, 欧进萍, 于达仁. 模糊向量真值修正模糊化方法[J].
模糊系统与数学, 2005, 18(3): 62-67.
Zhang J L, Ou J P, Yu D R. A fuzzifier with fuzzy vector revised by true values[J]. fuzzy systems and mathematics, 2005, 18(3): 62-67. |
| [12] |
李元松, 陈文峰, 李新平. 基于模糊神经网络的边坡稳定性评价方法[J].
武汉理工大学学报, 2013, 35(1): 113-118.
Li Y S, Chen W F, Li X P. Evaluation approach of slope stability based on fuzzy neural network[J]. Wu Han University of Technology, 2013, 35(1): 113-118. |
| [13] |
周宁, 傅鹤林, 袁勇. 基于模糊神经网络的边坡稳定性评价方法[J].
地下空间与工程学报, 2009, 5(A02): 1826-1832.
Zhou L, Fu H L, Yuan Y. Evaluation approach of slope stability based on fuzzy neural network[J]. Chinese Journal of Underground Space and Engineering, 2009, 5(A02): 1826-1832. |
| [14] |
周伟, 张生瑞, 高行山. 基于模糊理论和神经网络技术公路网综合评价方法研究[J].
中国公路学报, 1997, 10(4): 76-82.
Zhou W, Zhang S R, Gao X S. A study of comprehensive evaluation for the road network based on the fuzzy theory and neural network[J]. China Journal of Highway and Transport, 1997, 10(4): 76-82. |
| [15] |
薛新华, 姚晓东. 边坡稳定性预测的模糊神经网络模型[J].
工程地质学报, 2007, 15(1): 77-82.
Xue X H, Yao X D. A fuzzy neural network model for predicting slope stability[J]. Journal of Engineering Geology, 2007, 15(1): 77-82. |
| [16] |
朱大奇, 史慧.
人工神经网络原理及应用[M]. 科学出版社, 2006.
|
| [17] |
朱敏, 李悦, 孔范龙, 等. 基于MATLAB实现模糊神经网络模型在企业水环境中的应用[J].
绿色科技, 2012(5): 150-152.
Zhu M, Li Y, Kong F L, et al. Application of fuzzy neural network model to evaluation of enterprise water environment based on MATLAB[J]. Journal of Green Science and Technology, 2012(5): 150-152. |
| [18] |
李翔, 苏成, 王韶君. 基于模糊神经网络的综合评判方法[J].
计算机工程, 2009, 35(6): 200-201.
Li X, Su C, Wang S J. Comprehensive evaluation method based on fuzzy neural network[J]. Computer Engineering, 2009, 35(6): 200-201. |
 2015, Vol. 32
2015, Vol. 32

