如何有效地分析数据之中的因果关系,进行因果推断一直是数据分析研究领域的一个很重要的问题.虽然近年来很多学者提出了很多相关的研究成果[1-8],但如何在高维数据间推断其中的因果关系仍然没有一个有效的方法.
因果推断方法可以被分为两大类:贝叶斯网络结构学习算法[9-10]和基于加噪声模型的因果推断算法[11-13].其中,贝叶斯网络结构学习算法主要有两种方法.第一种是基于打分-搜索的贝叶斯网络结构学习方法,第二种是基于依赖分析的学习算法.然而,由于一个因果网络可能存在很多马尔科夫等价类.如果用评分函数去评价是同样的分数,从依赖关系来看,马尔科夫等价类间满足同样的条件独立性,因而没办法区分出哪个结构才是数据间真正的结构.在基于加噪声模型的算法方面,Shohei等人提出了一种基于线性ANM的算法[11],可以从数据集中构建出具体的因果网络图.然而这种算法只适用于线性加噪声模型,无法解决非线性问题.针对非线性问题,Hoyer等人提出了一种在基于非线性加噪声模型的适用于连续数据的算法(ANM)[12],Jonas Peters等人提出了一种基于非线性ANM的算法去解决离散数据的问题[13].然而,这两种非线性加噪声模型算法都只适用很低维的数据集,一旦数据集的维度较大(n>8),准确度就会降到很低.近来,Janzing D等人提出了一种基于信息熵的因果推断算法IGCI[14],这种算法可以适用于有无噪声的情况,但类似地,IGCI也无法处理高维数据,只要维数超过2,方法就失效.因而,目前还没有能适用于高维数据集有效的因果推断算法.
为了克服在高维数据中无法进行有效的因果推断的缺点,本文提出了一种基于条件独立性测试和互信息的因果网络结构学习算法.该算法首先利用条件独立性测试和互信息,求出每一个节点的父子节点,然后利用ANM算法,对目标节点与其每一个父子节点进行方向识别,然后得到每一个节点和其父子节点之间具体的因果关系,数据集中的所有变量都迭代完后得到数据集的一个完整因果网络图.数值实验表明,该算法在高维数据下,精确度和时间花费都要优于IGCI和基于加噪模型的因果网络结构学习算法.
1 预备知识 1.1 因果网络因果网络是表示变量间概率依赖关系的有向无环图(DAG),它可表示为一个三元组G=(N, E, P).其中,N={x1, x2, ..., xn}表示DAG中的所有节点的集合,每个节点代表一个变量(属性). E={e(xi, xj)|xi, xj∈ N }表示DAG中每两个节点间的有向边的集合.其中,e(xi, xj)表示xi, xj间存在依赖关系xi→xj. P={P(xi|xj)|xi, xj∈ N }是一组条件概率的集合,其中P(xi|xj)表示xi的父节点集xj对xi的影响.因果网络实质上就是一个联合概率分布P(x1, x2, …, xn)所有条件独立性的图形化表示.
1.2 d-分离准则d-分离准则是描述因果网络图的一个重要图性质.设X、Y、Z是因果无向图G中任意3个互不相交的节点的集合,称Z在图G中d-分离节点集X和Y,记为X⊥Y|Z, 如果对任意的从X的节点到Y的一个节点的路P均被Z阻断,也就是路径P上存在一个结点w满足下列其中一个条件:
(1) w在P上有—个碰撞箭头,即→w←(此时称w为碰撞点),且w及其后代结点都不在Z中.
(2) w在P上无碰撞箭头,即→w→或←w←或←w→,且w∈ Z.
1.3 条件独立性测试传统的贝叶斯结构学习算法主要是基于条件独立性测试,虽然这些算法无法区分马尔科夫等价类,从而无法发现数据间所蕴含的具体的因果关系,但在一定程度上,识别出了网络结构数据间的相关性,这对因果网络结构学习提供了很大的帮助. d-分离准则为图论和统计学间架设了一座桥梁,设X、Y、Z是因果无向图G中任意3个互不相交的节点的集合,如果Zd-分离节点集X和Y,那么在给定Z的情况下,X和Y统计独立.
1.4 互信息理论互信息是信息论中的一个重要概率,描述了某个变量取值对另外一个变量的取值能力.两个变量间的互信息越大,表明它们之间的关系紧密,反则越小.当且仅当X和Y互相独立的时候,它们之间的互信息I(X; Y)=0.
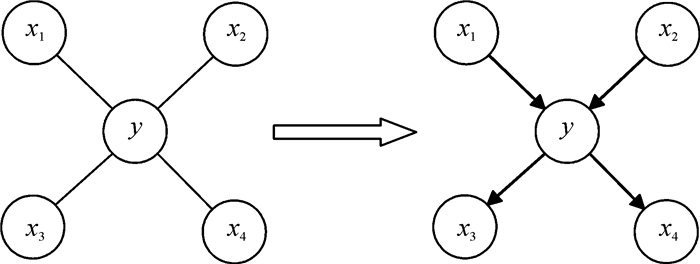
2 因果推断算法 2.1 算法的基本框架算法主要分为两部分,如图 1所示,算法的第一部分主要是利用条件独立性测试找出每一个目标节点的父子节点集,也就是一个以目标节点为中心的无向图.算法的第二部分是在已找出目标节点父子节点集的情况下,利用ANM算法对目标节点和每一个父子节点进行方向判别,得到一个目标节点与其父子节点间的具体因果关系.然后将该节点与其父子节点的因果结构更新到整个数据集的因果网络,直到每个节点和其父子节点集PC(y)的因果图都被更新完.最终得到一个完整地表现出数据间因果关系的因果网络图,从而推断出了数据间具体的因果关系.算法的两部分具体如下描述.
|
图 1 算法的基本框架 Figure 1 Algorithm framework |
如上述所说,这部分目的是找出每一个节点的父子节点.对于任意一个变量集X={x1, x2, ..., xn}, 在X中选出一个变量y作为目标节点,然后PC(y)表示y的候选的父子节点集.在算法开始时候,令PC(y)=X.
步骤1:对PC(y)中的每一个节点{x1, x2, ..., xn}和X进行独立性测试,如果xi和y独立,表明xi不是y的父子节点,将xi从PC(y)中移除.
步骤2:对PC(y)中的每对节点(xi, xj|xi, xj∈PC(y))进行条件独立性测试:Ind(y; xi|xj),如果xi和y在给定xj情况下条件独立,则表明xi不是y的父子节点.在经过独立性测试和条件独立性测试后,PC(y)维数已经降低很多,但依然有很多非父子节点没被移除.
步骤3:应用进一步的条件独立性测试:Ind(y; xi|S),S为PC(y)\xi的任意一个子集合,删掉非父子节点.
步骤4:由于条件独立性测试在给定条件集太大的情况下精确度会降低,从而可能导致非父子节点被错误地当做了父子节点,所以此时算法采取基于一个互信息的策略,对一部分错误加入到PC(y)的节点进行修剪.由于变量间依赖性可以用互信息描述,假设xi是y的父子节点,那xi和y之间的互信息不会太低,所以可以设定一个阈值p,计算PC(y)中每一个变量与y之间的互信息,如果它们之间的互信息小于p,则认为该变量不是y的父子节点,然后从PC(y)中删掉.
2.3 第二部分:对目标节点和其父子节点集PC(y)中每个节点进行方向识别在这部分,采用ANM算法对每个目标节点和其父子节点集间的边的方向进行判定.虽然ANM算法没办法解决超过8维的因果网络结构学习问题,但由于在算法第一部分已经得到了目标节点y的父子节点集合PC(y),然后利用ANM对PC(y)中的每一个变量和y间进行方向判别,这等同于在两点间应用ANM,从而保证了它的有效性.
3 数值实验数值实验是在Matlab2010b中完成,本文提出的算法被记为CIHD.实验中的条件独立性测试使用算法KCI-test[14], 计算互信息用Kraskov Mutual Information Estimator[16].在实验开始阶段,分两阶段生成实验数据. (1)生成因果网络图;(2)按照该图生成数据.在因果网络图生成阶段,分别生成15、25、50、80、150个节点的因果网络图,用来测试该算法在不同的高维数据下的实验效果.在数据生成阶段,每个节点的数据由因果网络图中节点的拓扑序列依照函数y=w1sin(x1)+w2sin(x2)+ε生成.其中w1、w2为每个函数的权值,随机取值于0.3与0.7之间,x1、x2为y的父亲节点,ε为权值为5%且均匀分布的添加噪声.为了有效地评价该算法的性能,引入了3个评价参数Precision、Recall和F-value,定义如下:
| $ \begin{array}{l} \;\;\;\;\;{\rm{Precision}} = \\ \frac{{\left\{ {{\rm{discovered\;causality}}} \right\} \cap \left\{ {{\rm{actual\; causality}}} \right\}{\rm{ }}}}{{\left\{ {{\rm{discovered\; causality}}} \right\}}}, \end{array} $ |
| $ {\rm{Recall}} = \frac{{\left\{ {{\rm{discovered\; causality}}} \right\} \cap \left\{ {{\rm{actual \;causality}}} \right\}}}{{\left\{ {{\rm{actual\; causality}}} \right\}}}, $ |
| $ \begin{array}{l} {\rm{F-value}} = \\ \frac{{2\left\{ {{\rm{discovered\; causality}}} \right\}\left\{ {{\rm{actual\; causality}}} \right\}}}{{\left\{ {{\rm{discovered\; causality}}} \right\} + \left\{ {{\rm{actual\; causality}}} \right\}}}. \end{array} $ |
从上面的定义可以看出,参数Precision用来衡量因果网络图中节点间本来不存在的边被错误添加的程度,而参数Recall用来衡量节点间存在的边没有被发现的程度.参数F-value是前两个评价参数的有机结合,因而可以用来评价因果网络结构学习算法的总体优劣.
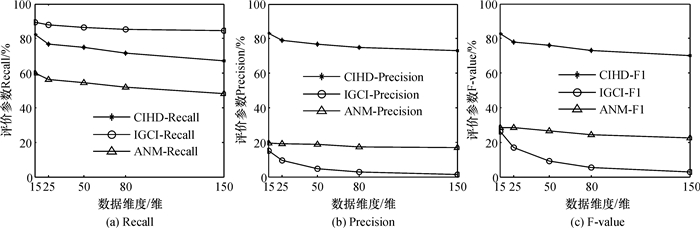
实验分别用15、25、50、80、150维的数据集对算法CIHD和基于非线性加噪模型的算法(ANM)以及IGCI进行对比,结果见图 2.
|
图 2 在不同维数下3种算法的评分参数 Figure 2 Different dimension of sample |
从图 2的实验结果可以看出,在数据集维度都较高的情况下,ANM算法和IGCI算法的学习准确度都很低,而CIHD算法在高维增加的情况下3个评价参数依然保持着较高的分数,说明在高维数据中,CIHD要大大优于另外两种算法.
4 结论本文提出了一种可以适应于高维数据的因果网络结构学习算法,首先通过基于条件独立性测试和互信息的方法对数据集进行初步结构学习,然后再利用ANM算法对数据集中每两点间的边进行方向识别,从而得到一个具体的因果网络结构.通过仿真表明,在维数增加时,该算法大大优于其他因果推断算法.
| [1] |
Pearl J. Causality: models, reasoning and inference[M]. Cambridge: MIT Press, 2000.
|
| [2] |
Spirtes P, Glymour C, Scheines R. Causation, prediction, and search[M]. Cambridge: MIT Press, 2000.
|
| [3] |
Uhler C, Raskutti G, Bühlmann P, et al. Geometry of the faithfulness assumption in causal inference[J].
The Annals of Statistics, 2013, 41(2): 436-463.
DOI: 10.1214/12-AOS1080. |
| [4] |
Cai R, Zhang Z, Hao Z. BASSUM: A Bayesian semi-supervised method for classification feature selection[J].
Pattern Recognition, 2011, 44(4): 811-820.
DOI: 10.1016/j.patcog.2010.10.023. |
| [5] |
Shimizu S, Hoyer P O, Hyvärinen A. Estimation of linear non-Gaussian acyclic models for latent factors[J].
Neurocomputing, 2009, 72(7): 2024-2027.
|
| [6] |
Hoyer P O, Shimizu S, Kerminen A J, et al. Estimation of causal effects using linear non-Gaussian causal models with hidden variables[J].
International Journal of Approximate Reasoning, 2008, 49(2): 362-378.
DOI: 10.1016/j.ijar.2008.02.006. |
| [7] |
Janzing D, Scholkopf B. Causal inference using the algorithmic Markov condition[J].
IEEE Transactions on Information Theory, 2010, 56(10): 5168-5194.
DOI: 10.1109/TIT.2010.2060095. |
| [8] |
陈锡枢. 基于贝叶斯网络下的遗传算法[J].
广东工业大学学报, 2007, 24(1): 19-21.
Chen X S. The genetic algorithm based on bayesian Net[J]. Journal of Guangdong University of Tehnology, 2007, 24(1): 19-21. |
| [9] |
Tsamardinos I, Brown L E, Aliferis C F. The max-min hill-climbing Bayesian network structure learning algorithm[J].
Machine learning, 2006, 65(1): 31-78.
DOI: 10.1007/s10994-006-6889-7. |
| [10] |
Shimizu S, Hoyer P O, Hyvärinen A, et al. A linear non-Gaussian acyclic model for causal discovery[J].
The Journal of Machine Learning Research, 2006, 7: 2003-2030.
|
| [11] |
Hoyer P O, Janzing D, Mooij J M, et al. Nonlinear causal discovery with additive noise models[C]//Advances in Neural Information Processing Systems. Vancouver, Canada: MIT Press, 2009: 689-696.
|
| [12] |
Peters J, Janzing D, Scholkopf B. Causal inference on discrete data using additive noise models[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(12): 2436-2450.
DOI: 10.1109/TPAMI.2011.71. |
| [13] |
Janzing D, Mooij J, Zhang K, et al. Information-geometric approach to inferring causal directions[J].
Artificial Intelligence, 2012, 56(10): 5168-5194.
|
| [14] |
Zhang K, Peters J, Janzing D, et al. Kernel-based conditional independence test and application in causal discovery[EB/OL]. (2012-02-14)[2013-10-24]. http://arxiv.org/ftp/arxiv/papers/1202/1202.3775.pdf.
|
| [15] |
Kraskov A, Stögbauer H, Grassberger P. Estimating mutual information[J].
Physical Review E, 2004, 69(6): 066138-066154.
DOI: 10.1103/PhysRevE.69.066138. |
 2015, Vol. 32
2015, Vol. 32