在工程实践中,针对具有不确定的动态控制系统,模糊If-then规则后件为模糊集的Mamdani型模糊逻辑系统是一种常见的逼近工具,并且逼近精度与模糊规则质量和数目紧密相关[1],由于Mamdani型模糊逻辑系统的输出可以写成一些模糊基函数的线性组合形式,因此产生了基于这些组合系数的模糊自适应控制方法[2-5],在这种模糊自适应控制方法中,自适应律的数目取决于模糊规则数目,这就造成了一种矛盾:一方面为了提高逼近精度和控制效果需要选用大量的模糊规则; 另一方面过多的自适应律往往会增大运算量和在线调节时间, 以至于导致闭环系统不稳定.
为了减少自适应律和在线运算量,文献[6]采用未知参数向量范数平方的Backstepping方法来降低自适应参数的数目; 文献[7]利用加装在模糊逻辑系统输入和输出端的伸缩器和饱和器, 通过调节伸缩器和饱和器的参数达到减少自适应律的目的.值得注意的是,这些研究方法中,规则前件中的隶属度函数在整个控制过程中是固定不变的,一般认为, 模糊隶属函数能够定量反映语言值的含义,隶属函数的确切定量描述有助于提高模糊逻辑系统的逼近精度[8].由于高斯型隶属度函数有最佳的逼近性能,当高斯型的隶属度函数的中心和宽度都固定时,上述模糊自适应方法意味着控制过程中即使系统的不确定性发生改变,相应的模糊隶属度函数也并不为之改变,这可能导致较大的逼近误差,降低控制性能,甚至造成控制失效.由此可见,如何依据有限条模糊If-then规则,改变以往根据逼近对象的采样或历史数据而构成的自适应模糊逻辑系统[9], 以控制目标为准则,着眼于规则前件的隶属函数,在线动态地调整高斯型隶属度函数的中心和宽度而构造相应的自适应律,从而改善被控系统的控制效果是一个值得研究的问题.
鉴于以上问题,针对一类非线性不确定系统,本文着眼于带有高斯型隶属度函数的有限多个模糊规则,首先将一个时变参数引入到规则前件中的高斯型隶属度函数之中, 形成一种带有可调参数的模糊逻辑系统, 然后依据控制目标, 利用这种带有可调参数的模糊逻辑系统逼近非线性系统中未知非线性函数,同时构造这个时变参数的更新律和原模糊逻辑系统逼近精度的自适应律,进而设计相应的自适应跟踪控制器.相比已有的一些模糊自适应控制方法[3-4, 10-11],本文提出的方法不仅减少了自适应参数的数目,而且简化控制器的设计步骤.最后,通过Duffing系统的仿真实例证明了本文方法的可行性和有效性.
1 系统描述 1.1 模糊系统描述由模糊产生器、模糊规则库、模糊推理机、解模糊器构成的Mamdani型模糊逻辑系统F,模糊规则库由以下N条模糊If-then规则构成:
| $ \begin{array}{l} {R_l}:{\rm{If}}\;{x_1}\;{\rm{is}}\;A_1^l\;{\rm{and}}\; \cdots \;{x_n}\;{\rm{is}}\;A_n^l,{\rm{then}}\;y\;{\rm{is}}\;{B^l}\;\left( {l = 1,} \right.\\ \left. {2, \cdots ,{\rm{N}}} \right), \end{array} $ | (1) |
这里z =[x1, x2, ..., xn]T ∈ Rn,y∈R分别为模糊逻辑系统的输入和输出, Ail和Bl为相应的模糊集合xi∈Ui∈ R, y∈V∈ R, Ui, V是相应的紧致集合.
根据文献[12], 采用单点模糊化、乘积推理和中心平均解模糊,模糊逻辑系统F的输出可以表示为
| $ F\left( \mathit{\boldsymbol{x}} \right) = \frac{{\sum\limits_{l = 1}^N {y_l^ * \prod\limits_{i = 1}^n {{\mu _{A_i^l}}\left( {{x_i}} \right)} } }}{{\sum\limits_{l = 1}^N {\prod\limits_{i = 1}^n {{\mu _{A_i^l}}\left( {{x_i}} \right)} } }}, $ | (2) |
这里μAil(xi)为模糊语言变量xi的隶属度函数,i=1, 2, …, n,本文选取高斯型隶属度函数,即
现在将一个时变参数θ=θ(t)引入到形如式(1)的模糊If-then规则前件的隶属度函数μAil(xi)中,形成带有时变参数的隶属度函数
| $ {\mu _{A_i^l}}\left( {\frac{{{x_i}}}{\theta }} \right) = \exp \left( { - {{\left( {\frac{{\frac{{{x_i}}}{\theta } - a_i^l}}{{b_i^l}}} \right)}^2}} \right), $ |
从而形成 N条带有参数的新规则:
| $ \begin{array}{l} {{\tilde R}_l}: = {\rm{If}}\;{x_1}\;{\rm{is}}\;\tilde A_1^l\;{\rm{and}}\; \cdots \;{x_n}\;{\rm{is}}\;\tilde A_n^l,{\rm{then}}\;y\;{\rm{is}}\;{B^l}\;\left( {l = 1,} \right.\\ \left. {2, \cdots ,{\rm{N}}} \right), \end{array} $ | (3) |
其中
基于模糊规则(3)的模糊逻辑系统记为
| $ \tilde F\left( \mathit{\boldsymbol{x}} \right) = F\left( {\frac{\mathit{\boldsymbol{x}}}{\theta }} \right) = \frac{{\sum\limits_{l = 1}^N {y_l^ * \prod\limits_{i = 1}^n {\exp \left( { - {{\left( {\frac{{\frac{{{x_i}}}{\theta } - a_i^l}}{{b_i^l}}} \right)}^2}} \right)} } }}{{\sum\limits_{l = 1}^N {\prod\limits_{i = 1}^n {\exp \left( { - {{\left( {\frac{{\frac{{{x_i}}}{\theta } - a_i^l}}{{b_i^l}}} \right)}^2}} \right)} } }}. $ | (4) |
注1 (1)从论域覆盖的角度看, 一组模糊规则的前件语言变量取值范围形成了对其输入论域的一组(完全或不完全)覆盖, 其中每一条规则对应于覆盖中的一个“补丁”[14].模糊规则(3)可以看作是模糊规则(1)的一种参数化形式, 由于参数θ=θ(t)的时变性,因此与规则(1)相比较,规则(3)中的“补丁”具有动态性, 因而规则(3)具有动态的语言可解释性. (2)本文将根据控制目标设计时变参数θ=θ(t的更新律,这意味着模糊规则(3)能够依据控制目标在线变化,而高斯型隶属度函数有全局支撑的性质(即隶属度函数值处处不为0),这也意味着当专家给出有限的语言信息(模糊If-then规则(1))时,通过时变参数θ的引入, 规则前件中的隶属函数的中心值和宽度实时地变化,派生出新的动态变化的模糊If-then规则,这不仅将原有规则(1)中的语言信息细化了,而且极大地丰富了原有的专家经验.
1.2 被控对象描述| $ \left\{ \begin{array}{l} {x^{\left( n \right)}} = \tilde f\left( {\mathit{\boldsymbol{x}},t} \right) + gu + d,\\ y = x, \end{array} \right. $ | (5) |
其中状态向量
定义x1=x,
x2=
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{B}}\left[ {\tilde f\left( {\mathit{\boldsymbol{x}},t} \right) + gu + d} \right],\\ y = x, \end{array} \right. $ | (6) |
其中
对于任意给定的可微参考信号r=r(t),记跟踪误差为e = e(t)=y(t)-r(t)=x(t)-r(t),误差各阶导数为
| $ \mathit{\boldsymbol{\dot e}} = \mathit{\boldsymbol{Ae}} + \mathit{\boldsymbol{B}}\left[ {\tilde f\left( {\mathit{\boldsymbol{x}},t} \right) + d + gu - {r^{\left( n \right)}}\left( t \right)} \right]. $ | (7) |
假设1 (1)在紧致闭集
注2 若∂f/∂xi(i=1, 2, …, n)在
假设2 在假设1成立的条件下,存在形如式(1)的模糊逻辑系统F和未知正常数 E使得
假设3 存在一个设计的正常数α满足
注3 在工程应用中
显然矩阵对(A, B)是完全可控的,即存在一个1×n阶矩阵K使得对于任意给定的正定矩阵Q, 下列Lyapunov方程有唯一正定矩阵解P:
| $ {\left( {\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}}} \right)^{\rm{T}}}\mathit{\boldsymbol{P}} + \mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}}} \right) = - \mathit{\boldsymbol{Q}}. $ | (8) |
为了表示方便,本文采用
| $ \mathit{\boldsymbol{\dot e}} = \mathit{\boldsymbol{Ae}} + \mathit{\boldsymbol{B}}\left[ {\tilde f\left( {\mathit{\boldsymbol{x}},t} \right) + d + gu - {r^{\left( n \right)}}\left( t \right)} \right], $ | (9a) |
| $ \dot \theta = x\left( {\mathit{\boldsymbol{e}},\theta ,\hat E,\hat L} \right), $ | (9b) |
| $ \dot {\hat L} = \vartheta \left( {\mathit{\boldsymbol{e}},\theta ,\hat E,\hat L} \right), $ | (9c) |
| $ \dot {\hat E} = \zeta \left( {\mathit{\boldsymbol{e}},\theta ,\hat E,\hat L} \right), $ | (9d) |
| $ u = u\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{e}},\theta } \right), $ | (9e) |
式(9a~9e)表示的扩展闭环系统的状态变量为Ζ=[eT, θ,
控制目标:设计形如式(9e)的控制器u和参数自适应律(9b~9d)使得扩展系统的状态变量Ζ =[eT, θ,
为了达到以上控制目标,本文提出如下控制方案:
| $ u = \left\{ \begin{array}{l} 0,\left\| \mathit{\boldsymbol{e}} \right\| > \left| \theta \right|\alpha ,\\ {u_1} + {u_2},\left\| \mathit{\boldsymbol{e}} \right\| \le \left| \theta \right|\alpha , \end{array} \right. $ | (10a) |
| $ \begin{array}{l} {u_1} = - F\left( {\frac{\mathit{\boldsymbol{x}}}{\theta }} \right),{u_2} = \mathit{\boldsymbol{Ke}} + \tau ,\tau = \\ \left\{ \begin{array}{l} - \frac{{{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{PB}}}}{{\left\| {{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{PB}}} \right\|{g_{\min }}}}\left[ {\left\| {\mathit{\boldsymbol{Ke}}} \right\|\left( {{g_{\max }} + 1} \right) + \omega \left( {\mathit{\boldsymbol{x}},t} \right) + } \right.\\ \;\;\;\left. {{d_{\max }} + \psi } \right],{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{PB}} \ne 0,\\ 0,{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{PB}} = 0. \end{array} \right. \end{array} $ | (10b) |
| $ \begin{array}{l} \dot \theta = \\ \left\{ \begin{array}{l} \frac{1}{{2\theta {\alpha ^2}}}\left\{ {\upsilon + 2\sqrt {n - 1} {{\left\| \mathit{\boldsymbol{e}} \right\|}^2} + 2\left\| \mathit{\boldsymbol{e}} \right\|\left\| \mathit{\boldsymbol{B}} \right\|\left[ {\hat L\alpha + } \right.} \right.\\ \;\;\;\;\left. {\left. {\omega \left( {\mathit{\boldsymbol{x}},t} \right) + {d_{\max }} + \psi } \right]} \right\},\left\| \mathit{\boldsymbol{e}} \right\| > \left\| \theta \right\|\alpha ,\\ - 2{\gamma _1}{\theta ^{ - 1}}\left\| \mathit{\boldsymbol{e}} \right\|\left\| {\mathit{\boldsymbol{PB}}} \right\|\left[ {\left( {\hat L\alpha \left| {\theta - 1} \right| + {g_{\max }}\hat E} \right.} \right],\\ \;\;\;\;\left\| \mathit{\boldsymbol{e}} \right\| \le \left\| \theta \right\|\alpha . \end{array} \right. \end{array} $ | (11) |
| $ \dot L = \left\{ \begin{array}{l} 2\beta \left\| \mathit{\boldsymbol{e}} \right\|\left\| \mathit{\boldsymbol{B}} \right\|\alpha ,\left\| \mathit{\boldsymbol{e}} \right\| > \left| \theta \right|\alpha ,\\ 2{\gamma _3}\alpha \left| {\theta - 1} \right|\left\| \mathit{\boldsymbol{e}} \right\|\left\| {\mathit{\boldsymbol{PB}}} \right\|,\left\| \mathit{\boldsymbol{e}} \right\| \le \left| \theta \right|\alpha . \end{array} \right. $ | (12) |
| $ \dot E = \left\{ \begin{array}{l} 0,\left\| \mathit{\boldsymbol{e}} \right\| > \left\| \theta \right\|\alpha ,\\ 2{\gamma _2}{g_{\max }}\left\| \mathit{\boldsymbol{e}} \right\|\left\| {\mathit{\boldsymbol{PB}}} \right\|,\left\| \mathit{\boldsymbol{e}} \right\| \le \left\| \theta \right\|\alpha . \end{array} \right. $ | (13) |
其中参数υ,β,γ1,γ2,γ3是可调正常数.
定理1 针对系统(7),在假设1~假设4成立的条件下,采用控制器(10a)~(10b)和参数自适应律(11)~(13), 能够保证扩展闭环系统(9a~9e)的状态向量Ζ =[eT, θ,
下面分两种情况证明定理1.
情形1
在这种情形下,采用开环控制,即u=0.在假设1和假设4成立的条件下, 首先可以证明状态向量Ζ =[eT, θ,
| $ \begin{array}{l} \dot V = s\left\{ {2{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{Ae}} + 2{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{B}}\left[ {f\left( \mathit{\boldsymbol{x}} \right) + o\left( {\mathit{\boldsymbol{x}},t} \right) + d - } \right.} \right.\\ \left. {\left. {{r^{\left( n \right)}}\left( t \right)} \right] - 2\theta \dot \theta {\alpha ^2} + {\beta ^{ - 1}}\tilde L\dot {\hat L}} \right\} \le \\ s\left\{ {2\sqrt {n - 1} {{\left\| \mathit{\boldsymbol{e}} \right\|}^2} + 2\left\| \mathit{\boldsymbol{e}} \right\|\left\| \mathit{\boldsymbol{B}} \right\|\left[ {\hat L\alpha + \omega \left( {\mathit{\boldsymbol{x}},t} \right) + {d_{\max }} + } \right.} \right.\\ \left. {\left. \psi \right] - 2\theta \dot \theta {\alpha ^2} + {\beta ^{ - 1}}\tilde L\left( {\hat L - 2\beta \left\| \mathit{\boldsymbol{e}} \right\|\left\| \mathit{\boldsymbol{B}} \right\|\alpha } \right)} \right\} = - \upsilon s. \end{array} $ | (14) |
由文献[15]的结果可知,不等式(14)意味着,状态向量Ζ =[eT, θ,
情形2
考虑正定函数V(t)= eTPe +0.5γ1-1θ2+0.5γ2-1
| $ \begin{array}{l} \mathit{\boldsymbol{\dot e}} = \left( {\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}}} \right)\mathit{\boldsymbol{e}} + \mathit{\boldsymbol{B}}\left[ {f\left( \mathit{\boldsymbol{x}} \right) + g{u_1}} \right] + \mathit{\boldsymbol{B}}\left[ { - \mathit{\boldsymbol{Ke}} + } \right.\\ \left. {o\left( {\mathit{\boldsymbol{x}},t} \right) + d - {r^{\left( n \right)}}\left( t \right) + g{u_2}} \right]. \end{array} $ | (15) |
V(t)沿着扩展闭环系统(9a~9e)关于时间t的导数为
| $ \begin{array}{l} \dot V\left( t \right) = - {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{Qe}} + 2{e^{\rm{T}}}\mathit{\boldsymbol{PB}}\left[ {f\left( \mathit{\boldsymbol{x}} \right) + g{u_1}} \right] + \\ 2{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{PB}}\left[ { - \mathit{\boldsymbol{Ke}} + o\left( {\mathit{\boldsymbol{x}},t} \right) + d - {r^{\left( n \right)}}\left( t \right) + g{u_2}} \right] + \\ \gamma _1^{ - 1}\theta \dot \theta + \gamma _2^{ - 1}\tilde E\dot {\hat E} + \gamma _3^{ - 1}\tilde L\dot {\hat L}. \end{array} $ | (16) |
利用式(10b)得
| $ \begin{array}{l} 2{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{PB}}\left[ { - \mathit{\boldsymbol{Ke}} + o\left( {\mathit{\boldsymbol{x}},t} \right) + d - {r^{\left( n \right)}}\left( t \right) + g{u_2}} \right] \le \\ \left\| {{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{PB}}} \right\|\left[ {\left\| {\mathit{\boldsymbol{Ke}}} \right\|\left( {{g_{\max }} + 1} \right) + \omega \left( {\mathit{\boldsymbol{x}},t} \right) + {d_{\max }} + \psi } \right]\left[ {1 - } \right.\\ \left. {\frac{g}{{{g_{\min }}}}} \right] \le 0, \end{array} $ | (17) |
| $ \begin{array}{l} 2{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{PB}}\left[ {f\left( x \right) + g{u_1}} \right] \le 2\left\| \mathit{\boldsymbol{e}} \right\|\left\| {\mathit{\boldsymbol{PB}}} \right\|\left[ {L\alpha \left\| {\theta - 1} \right\| + } \right.\\ \left. {{g_{\max }}E} \right], \end{array} $ | (18) |
所以由(16)~(18)得
| $ \begin{array}{l} \dot V\left( t \right) \le - {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{Qe}} + 2\left\| \mathit{\boldsymbol{e}} \right\|\left\| {\mathit{\boldsymbol{PB}}} \right\|\left[ {L\alpha \left\| {\theta - 1} \right\| + } \right.\\ \left. {{g_{\max }}E} \right] + \gamma _1^{ - 1}\theta\; \dot \theta + \gamma _2^{ - 1}\tilde E\dot {\hat E} + \gamma _3^{ - 1}\tilde L\dot {\hat L} = - {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{Qe + }}\\ \gamma _1^{ - 1}\theta \left\{ {2{\gamma _1}{\theta ^{ - 1}}\left\| \mathit{\boldsymbol{e}} \right\|\left\| {\mathit{\boldsymbol{PB}}} \right\|\left[ {\left( {\hat L\alpha \left\| {\theta - 1} \right\| + {g_{\max }}\hat E} \right.} \right] + } \right.\\ \left. {\dot \theta } \right\}\gamma _2^{ - 1}\tilde E\left( {\dot {\hat E} - 2{\gamma _2}{g_{\max }}\left\| \mathit{\boldsymbol{e}} \right\|\left\| {\mathit{\boldsymbol{PB}}} \right\|} \right) + \gamma _3^{ - 1}\tilde L\left( {\dot {\hat L} - } \right.\\ \left. {2{\gamma _3}\alpha \left\| {\theta - 1} \right\|\left\| \mathit{\boldsymbol{e}} \right\|\left\| {\mathit{\boldsymbol{PB}}} \right\|} \right). \end{array} $ | (19) |
利用式(11)~(13)可以得
| $ \mathit{\boldsymbol{\dot V}}\left( t \right) \le - {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{Qe}}. $ | (20) |
不等式(20)表明扩展闭环控制系统(9a)~(9e)的状态向量Ζ =[eT, θ,
推论1 考虑系统(5), 在定理1成立的条件下,在假设1~假设4成立的条件下,采用控制器(10a)~(10b)和参数自适应律(11)~(13), 能够保证系统(5)的输出跟踪误差
注4 (1)参数自适应律(11)~(13)具有下一特点:参数自适应律(12)和(13)在[0, +∞]上是单调递增的,因此初始条件
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2},\\ {{\dot x}_2} = - 0.1{x_2} - x_1^3 + 12\cos \left( t \right) + u\left( t \right),\\ y = {x_1}, \end{array} \right. $ | (21) |
将式(21)转化形如式(6)的形式后,
系统(21)在未控时状态呈现混沌.
情形1 在仿真的过程中,假设f(x)是未知的,记f(x)=-0.1x2-x13, 根据图 2可选取模糊系统的论域为
| $ {R_1}:{\rm{If}}\;{x_1}\;{\rm{is}}\;'N'\;{\rm{and}}\;{x_2}\;{\rm{is}}\;'N',{\rm{Then}}\;y\;{\rm{is}}\;y_1^ * = 100; $ |
| $ {R_2}:{\rm{If}}\;{x_1}\;{\rm{is}}\;'N'\;{\rm{and}}\;{x_2}\;{\rm{is}}\;'Z',{\rm{Then}}\;y\;{\rm{is}}\;y_2^ * = 100; $ |
| $ {R_3}:{\rm{If}}\;{x_1}\;{\rm{is}}\;'N'\;{\rm{and}}\;{x_2}\;{\rm{is}}\;'P',{\rm{Then}}\;y\;{\rm{is}}\;y_3^ * = 100; $ |
| $ {R_4}:{\rm{If}}\;{x_1}\;{\rm{is}}\;'Z'\;{\rm{and}}\;{x_2}\;{\rm{is}}\;'N',{\rm{Then}}\;y\;{\rm{is}}\;y_4^ * = 1; $ |
| $ {R_5}:{\rm{If}}\;{x_1}\;{\rm{is}}\;'Z'\;{\rm{and}}\;{x_2}\;{\rm{is}}\;'Z',{\rm{Then}}\;y\;{\rm{is}}\;y_5^ * = 0; $ |
| $ {R_6}:{\rm{If}}\;{x_1}\;{\rm{is}}\;'Z'\;{\rm{and}}\;{x_2}\;{\rm{is}}\;'P',{\rm{Then}}\;y\;{\rm{is}}\;y_6^ * = - 1; $ |
| $ {R_7}:{\rm{If}}\;{x_1}\;{\rm{is}}\;'P'\;{\rm{and}}\;{x_2}\;{\rm{is}}\;'N',{\rm{Then}}\;y\;{\rm{is}}\;y_7^ * = - 100; $ |
| $ {R_8}:{\rm{If}}\;{x_1}\;{\rm{is}}\;'P'\;{\rm{and}}\;{x_2}\;{\rm{is}}\;'Z',{\rm{Then}}\;y\;{\rm{is}}\;y_8^ * = - 100; $ |
| $ {R_9}:{\rm{If}}\;{x_1}\;{\rm{is}}\;'P'\;{\rm{and}}\;{x_2}\;{\rm{is}}\;'P',{\rm{Then}}\;y\;{\rm{is}}\;y_9^ * = - 100. $ |
|
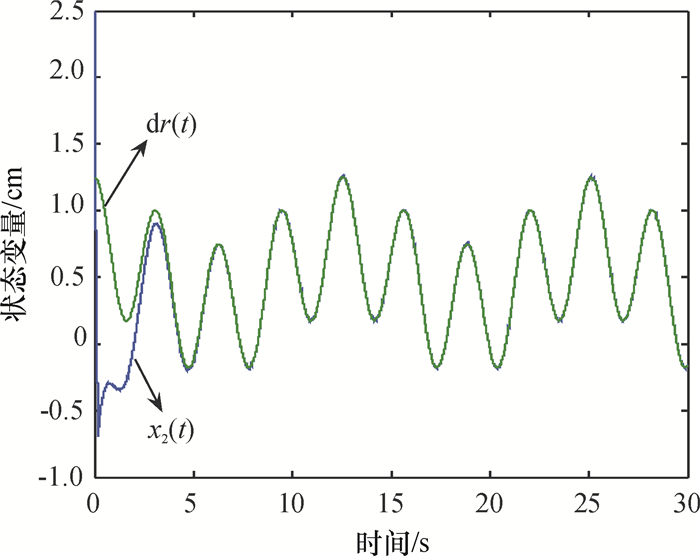
图 2 参考信号为r(t)=0.5(sin(0.5t)+0.5sin(2t))时状态x2(t)的跟踪轨迹 Figure 2 The tracking trajectories of x2(t) for the reference signal r(t)=0.5(sin(0.5t)+0.5sin(2t)) |
选取K =[-1, -2], Q =diag[10, 10], 初始条件x1(0)=x2(0)=2, θ(0)=1,
|
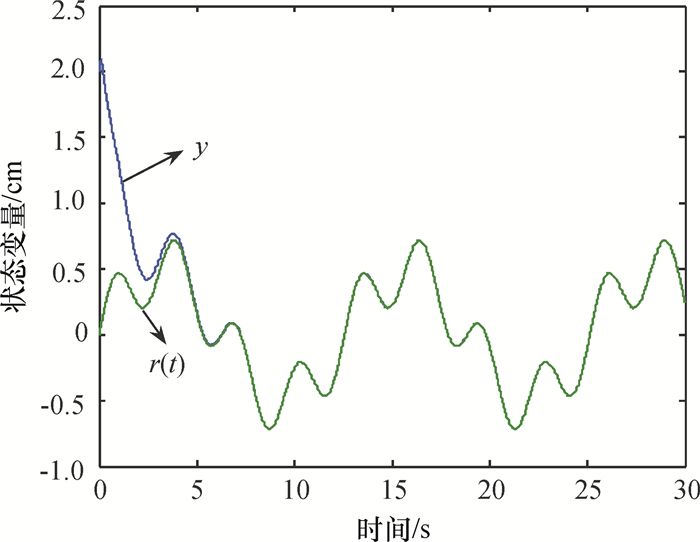
图 1 参考信号为r(t)=0.5(sin(0.5t)+0.5sin(2t))时的输出跟踪轨迹 Figure 1 Output tracking trajectories for the reference signal r(t)=0.5(sin(0.5t)+0.5sin(2t)) |
|
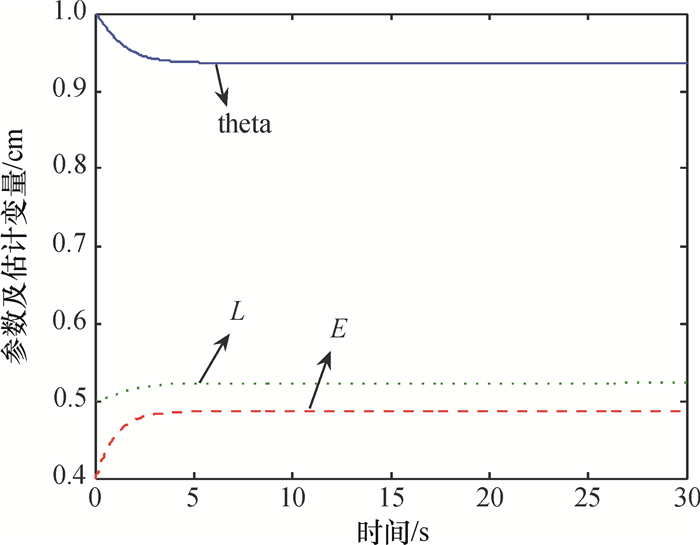
图 3 时变参数θ以及参数L和E的估计量的时间响应曲线 Figure 3 The time response of time-varying parameter θ and the estimated values of L and E |
注5 (1)由图 1~图 3可以看出不但系统的输出可以渐近地跟踪输入信号,而且系统的其他状态不但保证了有界同时也实现良好的跟踪,同时所有自适应参数有界;(2)自适应律仅有3个,保证了控制算法运算量小.
情形2 作为对比仿真,本文采用文献[9]的模糊多模型自适应控制(FMMAC).选择K =[6,5]T, Q=diag[10,10],采用情形1的模糊论域及模糊划分,参考信号r(t)=sin(t),初始条件x1(0)=x2(0)=2,文献[1]中的自适应参数向量
|
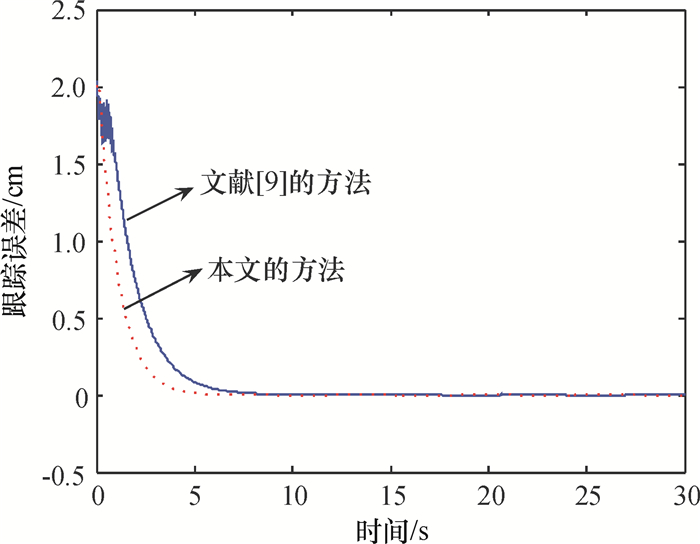
图 4 参考信号为r(t)=sin(t)时本文与文献[9]中系统输出跟踪误差的时间响应曲线 Figure 4 The time response of the output tracking errors in this paper and [9] for the reference signal r(t)=sin(t) |
|
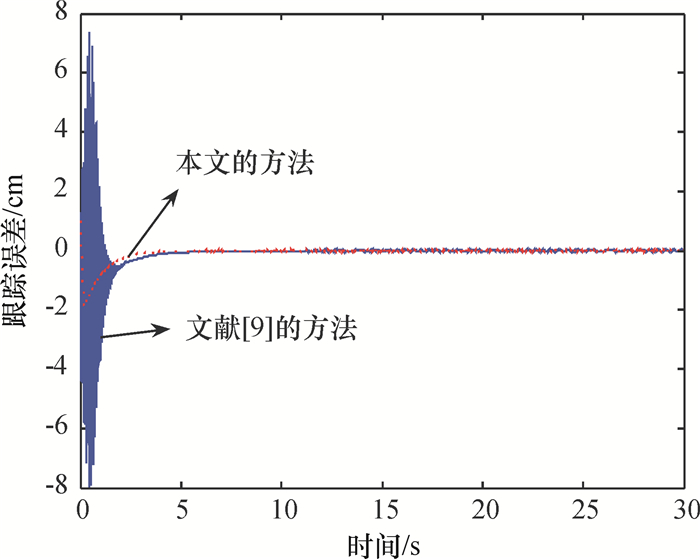
图 5 参考信号为r(t)=sin(t)时本文与文献[9]中系统的状态x2的跟踪误差的时间响应曲线 Figure 5 The time response of the tracking errorsx2in this paper and [9] for the reference signal r(t)=sin(t) |
注6 (1)由对比图 4的输出跟踪误差可以发现,本文提出自适应控制方法不仅可以保证输出跟踪误差渐近地趋近于零,而且响应的速度要比文献[9]更快; (2)由对比图 5可以看出,文献[9]中系统的状态x2的跟踪误差在开始阶段是震荡的,因此本文提出的自适应控制算法的状态跟踪效果要优于文献[9].
4 结论本文主要着眼于当专家给出一组有限数目的模糊规则时,首先将一个时变参数引入到这组模糊规则前件的高斯隶属函数中将原有规则参数化.通过时变参数的变化,改变了高斯隶属函数的中心和宽度,进而改变了原模糊逻辑系统的输出,从而得到一种新的带有时变参数的Mamdani模糊逻辑系统.如果利用这种新的模糊逻辑系统逼近系统中未知的非线性函数,并且以此为基础构造控制器和自适应律, 那么所给出的模糊自适应控制方法不仅能够保证被控系统的输出跟踪误差渐近趋近于零,而且与现有的模糊自适应控制方法相比较, 具有较少的自适应律和较强的模糊逻辑系统规则的语言可解释性.
| [1] |
Wang L X, Mendel J M. Fuzzy basis functions, universal approximation and orthogonal least squares learning[J].
IEEE Trans on Neural Networks, 1992, 3(5): 807-814.
DOI: 10.1109/72.159070. |
| [2] |
Chen B, Liu X P, Tong S C. Adaptive fuzzy output tracking control of MIMO nonlinear uncertain systems[J].
IEEE Trans on Fuzzy Systems, 2007, 15(2): 287-300.
DOI: 10.1109/TFUZZ.2006.880008. |
| [3] |
Wang L X. Stable adaptive fuzzy controllers with application to inverted pendulum tracking[J].
IEEE Trans on Systems, Man, and Cybernetics-part B: Cybernetics, 1996, 26(5): 677-691.
DOI: 10.1109/3477.537311. |
| [4] |
Hwang E J, Hyun C H, Kim E, et al. Fuzzy model based adaptive syschronization chaotic systems:robust tracking control approach[J].
Physics Letters A, 2009, 373(22): 1935-1939.
DOI: 10.1016/j.physleta.2009.03.057. |
| [5] |
Kim E. A fuzzy disturbance observer and its application to control[J].
IEEE Trans Fuzzy Syst, 2002, 10(1): 77-84.
DOI: 10.1109/91.983280. |
| [6] |
Chen B, Liu X P, Liu K F, et al. Direct adaptive fuzzy control of nonlinear strict-feedback systems[J].
Automatica, 2009, 45(6): 1530-1535.
DOI: 10.1016/j.automatica.2009.02.025. |
| [7] |
范永青, 王银河, 罗亮, 等. 带有伸缩器和饱和器的一类非线性系统模糊自适应控制设计[J].
控制理论与应用, 2011, 28(9): 1105-1110.
Fan Y Q, Wang Y H, Luo L, et al. Fuzzy adaptive control design for a class of nonlinear systems with scalers and saturators[J]. Control Theory and Applications, 2011, 28(9): 1105-1110. |
| [8] |
Han H G, Su C Y, Yury S. Adaptive control fo a class of nonlinear systems with nonlinearly parameterized fuzzy approximators[J].
IEEE Trans on Fuzzy Systems, 2001, 9(2): 315-323.
DOI: 10.1109/91.919252. |
| [9] |
高子林, 王银河, 石炳杰. 基于自适应模糊逻辑系统的一类非线性系统跟踪控制设计[J].
广东工业大学学报, 2012, 29(9): 77-81.
Gao Z L, Wang Y H, Shi B J. Design of tracking control for a class of nonlinear systems based on adaptive fuzzy logic systems[J]. Journal of Guangdong University of Technology, 2012, 29(9): 77-81. |
| [10] |
Zhou Y H. Fuzzy indirect adaptive control using SVM-based multiple models for a class of nonlinear systems[J].
Neural Computing & Applications, 2013, 22(3-4): 825-833.
|
| [11] |
Tong S C, Li Y M. Observer-based fuzzy adaptive control for strict-feedback nonlinear systems[J].
Fuzzy Sets and Systems, 2009, 160(12): 1749-1764.
DOI: 10.1016/j.fss.2008.09.004. |
| [12] |
王立新.
模糊系统与模糊控制教程[M]. 北京: 清华大学出版社, 2003.
|
| [13] |
王国俊.
计算智能[M]. 2版. 北京: 高等教育出版社, 2005.
|
| [14] |
Bart K. Fuzzy engineering[M]. Upper Saddle River, USA: Prentice Hall, Inc., 1997.
|
| [15] |
Slotine J E, Li W P. Applied Nonlinear Control[M]. Englewood Cliffs, NJ: Prentice Hall, Inc., 1991.
|
 2015, Vol. 32
2015, Vol. 32