2. 广东工业大学 应用数学学院, 广东 广州 510520;
3. 广东省电信规划设计院有限公司 研发中心, 广东 广州 510630
2. School of Applied Mathematics, Guangdong University of Technology, Guangzhou 510520, China;
3. Research and Development Center, Guangdong Planning and Designing Institute of Telecommunications Company, Guangzhou 510630, China
基于多载波调制的OFDM系统,由于具有较高的频率利用率、抗多径衰落能力强等优点,已被广泛应用于无线通信技术中,如LTE和WIMAX等,但是其中存在一个不可避免的缺点,即由于多个独立的调制子载波同一时刻幅度叠加会导致较大的峰均比(PAPR),如果超过发射端高功率线性放大器的线性范围,高的PAPR会引起非线性失真,从而造成带外功率泄漏影响相邻频带的信号传输和带内子载波间的干扰造成系统的误比特率(Bit Error Rate, BER)性能下降.导致发送端对高功率放大器的线性要求很高,且发送效率降低,还会增加数模/模数转换器的复杂度.
目前有很多方法用来降低PAPR,如文献[1-2]所述,限幅滤波技术(Clipping and Filtering)[3]、编码技术、选择映射技术(SLM)、部分传输序列技术(PTS)、脉冲序列技术(PS)、子载波预留(TR)[4]等.其中限幅滤波技术是一种非常直接和有效降低峰均比的方法,但由于该过程是一个非线性过程,将导致严重的带内干扰和带外噪声.文献[5-6]提出了改进的算法,但是以算法复杂度的提高为代价.TR是Tellado和Cioffi提出的一种通过预留部分空子载波方法降低子载波之间的相关性来降低OFDM信号的峰均比,从而能够很好地改变限幅噪声频谱,但PAPR抑制的效果取决于预留子载波的数量和在频率矢量中的位置[7-8].文献[9-10]提出了改进的算法,收敛速度得到提升.文献[11]提出一种基于限幅滤波的改进子载波预留方法,考虑了结合两种方法的优点,但效果并不很理想.
本文在以上研究工作的基础上,提出了基于预留子载波功率分配的方案以改善峰均比降低的性能,最后给出了相应性能仿真分析比较.
1 OFDM系统中PAPR的定义及TR算法 1.1 PAPR的定义考虑一个具有N个子载波的OFDM系统,长度为N的复频域符号序列,经过OFDM调制器后生成的连续时间等效基带OFDM信号为
| $ s\left( t \right) = \frac{1}{{\sqrt N }}\sum\limits_{k = 0}^{N - 1} {{S_k}{{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}kt}}{{NT}}}}} ,\;\;\;\;\;\;\;t \in \left[ {0,NT} \right], $ | (1) |
其中Sk是第k个子载波上的复频域符号,Sk=(S0, S1, …, SN-1),T为OFDM符号的时间长度,缩放因子
| $ \begin{array}{l} {s_n} = {\rm{IDF}}{{\rm{T}}_1}\left( {{S_k},LN} \right) = \frac{1}{{\sqrt N }}\sum\limits_{k = 0}^{N - 1} {{S_k}{{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}kn}}{{NL}}}}} ,n = 0,1,\\ \cdots ,LN - 1.\\ {S_k} = {\rm{DF}}{{\rm{T}}_1}\left( {{s_n},LN} \right) = \frac{1}{{\sqrt N }}\sum\limits_{n = 0}^{N - 1} {{s_n}{{\rm{e}}^{ - {\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}kn}}{{NL}}}}} ,n = 0,1,\\ \cdots ,LN - 1. \end{array} $ | (2) |
其中L为过采样因子,sn为过采样后时域信号,Sk为对应频域信号.sn的实部和虚部分别为零均值实高斯随机变量,方差为
| $ {\rm{PAPR}}\left( {{s_n}} \right) = 10\lg \frac{{\mathop {\max }\limits_{0 \le n \le LN - 1} {{\left| {{s_n}} \right|}^2}}}{{E\left[ {{{\left| {{s_n}} \right|}^2}} \right]}}. $ | (3) |
在传统TR方法中,发送端和接收端都预先预留了一部分信噪比差的子载波用于降低PAPR的信号,而不用于携带数据.子载波预留原理如图 1所示.通过把降峰信号约束在由预留子载波产生的子空间内,符号序列中非零序列的位置为PM={p1, p2, …, pM},符号长度为LN的预留子载波的非零序列的位置为QR={q1, q2, …, qR},因此R+M=N, 经过处理后的符号表示为
| $ {{\bar S}_n} = {s_n} + \mu {c_n} = \frac{1}{{\sqrt N }}\sum\limits_{k = 0}^{N - 1} {\left( {{S_k} + \mu {C_k}} \right){{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}kn}}{{NL}}}}} , $ | (4) |

|
图 1 子载波预留原理图 Figure 1 principle for tone reservation |
其中数据向量和降峰向量在频域上是相互独立的,即SkCk=0.
由式(3)可以得到目标函数为
| $ \begin{array}{l} \mathop {\min }\limits_{{c_n}} \left\{ {{\rm{PAPR}}\left( {{s_n} + \mu {c_n}} \right)} \right\} = \\ \mathop {\min }\limits_{{c_n}} {\left\{ {10\lg \frac{{\mathop {\max }\limits_{0 \le n \le LN - 1} {{\left| {{s_n} + \mu {c_n}} \right|}^2}}}{{E\left[ {{{\left| {{s_n} + \mu {c_n}} \right|}^2}} \right]}}} \right\}}. \end{array} $ | (5) |
文献[12]提出的一种改进目标函数的思想,对于非线性性,最大化信号失真功率比(SDR)是一种更容易接受的检测传输信号质量和抑制峰均比的方法,目标函数(5)改进为:
| $ \mathop {\max }\limits_{{c_n}} {\rm{SDR = }}\mathop {\max }\limits_{{c_n}} \left\{ {\frac{{\left\| {{s_n}} \right\|_2^2}}{{\left\| {{{\bar S}_n} - {s_n}} \right\|_2^2}}} \right\}. $ | (6) |
文献[13]将子载波预留的非线性情况简化为软限幅器(Soft Limiter,SL)情况,发送端使用SL对其进行软包络限幅引入的失真是确定性的,即因为限幅操作而产生的OFDM信号特征改变是确定性的,利用一阶线性展开时域模型和离散功率谱频域模型进行分析[14].
sn服从复高斯分布,可以使用一阶线性展开时域模型,即
| $ {{\bar S}_n} = \varphi \left( {{s_n},{d_n}} \right) = \alpha {s_n} + {d_n}. $ | (7) |
运用离散功率谱频域模型,对应频域信号模型表示为
| $ {{\bar S}_k} = \alpha {S_k} + {D_k}, $ | (8) |
其中αsn为衰减信号分量,dn为失真分量,而衰减信号分量与失真分量线性无关,即E[sndn*]=0,α为衰减因子,α∈(0, 1],dn*为dn的共轭函数.
| $ \begin{array}{l} \alpha = \frac{{E\left[ {{s_n}\bar S_n^ * } \right]}}{{E\left[ {{s_n}s_n^ * } \right]}} = \frac{1}{{{P_s}}}\int_{ - \infty }^\infty {\lambda \varphi \left( {\lambda ,d} \right){f_{{s_n}}}\left( \lambda \right){\rm{d}}\lambda } \\ = 1 - {{\rm{e}}^{ - {\gamma ^2}}} + \frac{{\sqrt {\rm{ \mathsf{ π} }} }}{2}\gamma \times {\rm{erfc}}\left( \gamma \right), \end{array} $ | (9) |
其中fsn(λ)为sn的概率密度函数,
| $ \gamma = \frac{A}{{\sqrt {{P_s}} }}, $ |
| $ {\rm{erfc}}\left( \gamma \right) = \frac{2}{{\sqrt {\rm{ \mathsf{ π} }} }}\int_\gamma ^\infty {{{\rm{e}}^{ - {t^2}}}{\rm{d}}t} . $ |
当sn的功率谱为矩形时,Psk=(1-e-γ2)PSk,即得
| $ {P_{{D_k}}} = {P_{{{\bar S}_k}}} - {\alpha ^2}{P_{{S_k}}} = \left( {1 - {{\rm{e}}^{ - {\gamma ^2}}} - {\alpha ^2}} \right){P_{{S_k}}}. $ | (10) |
本文的目标函数是基于式(6)得到的频域变换表达式,即
| $ \mathop {\max }\limits_{{C_k}} {\rm{SDN}}{{\rm{R}}_k} = \mathop {\max }\limits_{{C_k}} \frac{{{\alpha ^2}{P_{{S_k}}}}}{{{P_w} + {P_{{D_k}}}}}. $ | (11) |
其中信号失真噪声比(SDNR)表征衰减信号分量功率与频域失真分量功率和信道噪声功率的比值.
下面对算法及求解过程进行详细介绍.
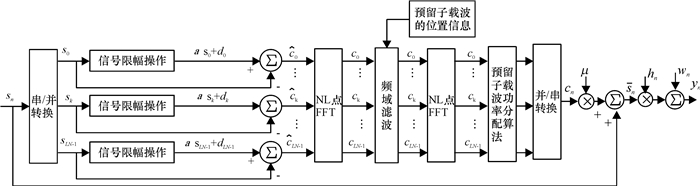
2.2 算法框架算法步骤如图 2所示.
|
图 2 算法发送端框图 Figure 2 The block diagram of the proposed algorithm in transmitter |
步骤1:将经过采样操作的时域信号sn,进行串/并转换操作分为LN个子载波块,即:sn=(s0, s1, …, sk, …, sLN-1).
步骤2:对各子载波块进行限幅操作,预先设定一个幅度阈值A,信号幅度小于阈值的信号不做处理,幅度大于预设阀值时进行削峰操作,即:
| $ {{\hat s}_n} = \left\{ \begin{array}{l} {s_n},{\rm{if}}\left| {{s_n}} \right| \le A;\\ A\frac{{{s_n}}}{{\left| {{s_n}} \right|}},{\rm{otherwise}}{\rm{.}} \end{array} \right. $ |
令
步骤3:对
| $ {{\hat C}_k} = \sum\limits_{n = 0}^{LN - 1} {{{\hat c}_n}w_{n,k}^ * } . $ |
其中wn, k*为第n个抽样点,第k个预留子载波的傅里叶系数,
| $ {w_{n,k}} = \frac{1}{{\sqrt N }}{{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}q{k^n}}}{{NL}}}},k = \left[ {1, \cdots ,R} \right],n = \left[ {0, \cdots ,LN - 1} \right]. $ |
步骤4:进行频域滤波,原理如图 3所示,将预留子载波位置处QR分别置为Cqk,数据子载波位置处PM分别置为0,
| $ {C_K} = H\left[ {{{\dot C}_k}} \right] = \left\{ \begin{array}{l} {{\hat C}_k},\;n \in {{\bf{Q}}_R};\\ 0,\;n \in {P_M}. \end{array} \right. $ |

|
图 3 频域滤波原理图 Figure 3 Principle for filtering in the frequency domain |
步骤5:对Ck进行LN点IFFT操作,转换为时域.
| $ {{\bar c}_n} = \sum\limits_{k = 0}^{NL - 1} {{C_k}{w_{n,k}}} = \sum\limits_{k = 1}^R {{{\hat C}_k}{w_{n,k}}} . $ |
步骤6:运用牛顿迭代法进行预留子载波的功率分配.
步骤7:将cn进行并/串转换生成预留子载波信号cn,与原信号sn进行加权和后进入信号放大器发送.时域信号表示为Sn=sn+μcn,对应频域信号表示为
| $ {{\bar S}_k} = {S_k} + \mu {{\bar c}_k}, $ | (12) |
其中μ为缩放系数,由后面牛顿迭代法确定.
根据一阶线性展开时域模型和离散功率谱频域模型,由式(12)得
| $ {P_{{S_k}}} = \frac{{{\mu ^2}}}{{ - {{\rm{e}}^{ - {\gamma ^2}}}}}{P_{{C_k}}}. $ | (13) |
将式(10)和(13)代入式(11)得
| $ {\rm{SDN}}{{\rm{R}}_k} = \frac{{{\alpha ^2}{\mu ^2}{P_{{C_k}}}}}{{\left( { - {{\rm{e}}^{ - {\gamma ^2}}}} \right){P_W} + {\mu ^2}\left( {1 - {{\rm{e}}^{ - {\gamma ^2}}} - {\alpha ^2}} \right){P_{{C_k}}}}}. $ | (14) |
为表述方便,令xk
根据式(11)得,目标函数为系统总的SDNR最大时的预留子载波功率向量,因为数据流在各个相互独立的子信道上传递,那么对于给定信道状态时的系统SDNR可以由算术平均值得到,即
| $ {\rm{SDN}}{{\rm{R}}_{{\rm{sys}}}} = \frac{1}{R}\sum\limits_{k = 1}^R {f\left( {{x_k}} \right)} . $ | (15) |
约束条件为预留子载波总功率受限,即令为一个常数,初始状态时,预留子载波的功率是平均分配的,即
| $ \sum\limits_{k = 1}^R {{x_k}} = R\bar P. $ | (16) |
所以得到数学模型为
| $ \begin{array}{l} \mathop {\max }\limits_{\left\{ {{x_k}} \right\}} {\rm{SDN}}{{\rm{R}}_{sys}}\\ {\rm{s}}.{\rm{t}}.\;\;\;\;\;\;\;\;\;\;\sum\limits_{k = 1}^R {{x_k}} = R\bar P. \end{array} $ |
为了求解上述模型,联立式(15)(16), 使用Lagrange乘法求解,Lagrange函数表示为
| $ J\left( {{x_1},{x_2}, \cdots ,{x_R}} \right) = \frac{1}{R}\sum\limits_{k = 1}^R {f\left( {{x_k}} \right)} + \lambda \left( {\sum\limits_{k = 1}^R {{x_k}} - R\bar P} \right), $ | (17) |
λ为Lagrange乘法因子.式(17)对xk求导并设为0,可以得到R个等式:
| $ \frac{1}{k}\frac{{\rm{d}}}{{{\rm{d}}{x_k}}}f\left( {{x_k}} \right) + \lambda = 0,\;\;\;k = 1,2, \cdots ,R. $ | (18) |
所以由式(16)和(18)中的R +1个等式来求解最优的功率分配.本文采用牛顿迭代法进行求解.上述方程组可以表示为
| $ \left\{ \begin{array}{l} {g_1}\left( {{x_1}, \cdots ,{x_R}} \right) = \frac{1}{R}f'\left( {{x_1}} \right) + \lambda = 0,\\ \;\;\;\;\;\;\;\; \vdots \\ {g_R}\left( {{x_1}, \cdots ,{x_R}} \right) = \frac{1}{R}f'\left( {{x_R}} \right) + \lambda = 0,\\ {g_{R + 1}}\left( {{x_1}, \cdots ,{x_R}} \right) = {x_1} + \cdots + {x_R} - R\bar P = 0. \end{array} \right. $ |
其中,
| $ X = {\left( {{x_1}, \cdots ,{x_R}} \right)^{\rm{T}}} \in {{\bf{R}}^n}, $ |
| $ G = \left( {{g_1}, \cdots ,{g_R},{g_{R + 1}}} \right), $ |
即该方程组可以表示为G(X)=0,
该方程组的Jacobi矩阵为
| $ \begin{array}{l} G'\left( X \right) = \\ {\left( {\begin{array}{*{20}{c}} {\frac{1}{R}f''\left( {{x_1}} \right)}&0& \cdots &0\\ \vdots&\ddots &{}&{}\\ 0&0& \cdots &{\frac{1}{R}f''\left( {{x_R}} \right)}\\ 1&1& \cdots &1 \end{array}} \right)_{\left( {R + 1} \right) \times \left( {R + 1} \right)}}. \end{array} $ |
所以迭代解为
| $ \begin{array}{l} {X^{\left( {m + 1} \right)}} = {X^{\left( m \right)}} - G'{\left( {{X^{\left( m \right)}}} \right)^{ - 1}} \times G\left( {{X^{\left( m \right)}}} \right),\\ m = 1,2, \cdots ,M. \end{array} $ |
其中m为迭代次数,式(12)中,根据文献[15]得,
通过Matlab软件对本文提出的算法的性能进行仿真分析, 仿真中采用的参数如表 1所示.
| 表 1 仿真参数 Table 1 Simulation parameters |
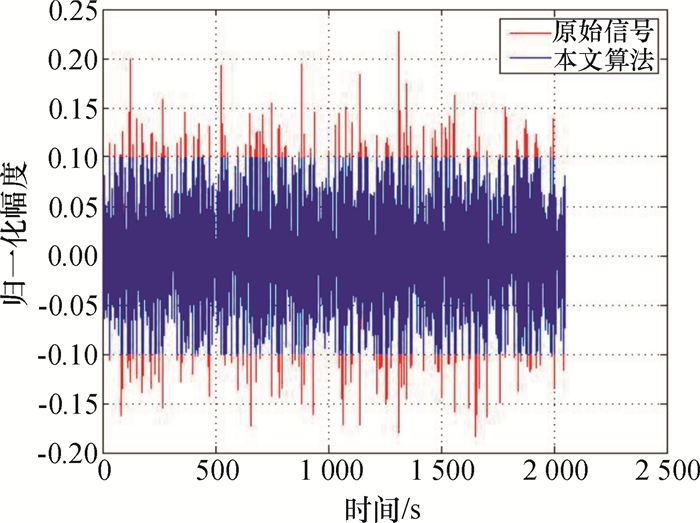
仿真1 OFDM系统PAPR效果时域幅度和频域功率谱密度仿真.图 4给出在一个OFDM符号周期内,在表 1的限幅比条件下的幅度降低的效果图,此时限幅门限A=2.5,限幅后信号的平均功率PS=
|
图 4 时域PAPR降低效果 Figure 4 PAPR reduction in time domain |
|
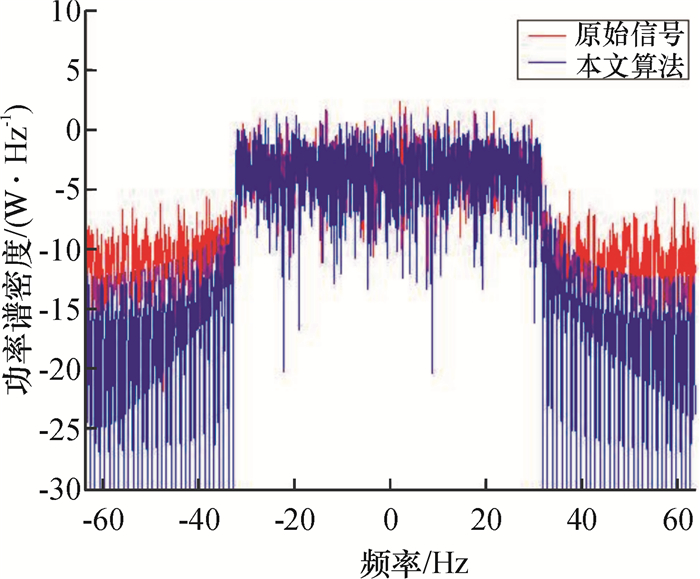
图 5 频域功率谱密度效果 Figure 5 PSD in frequency domain |
仿真2 与已有算法CCDF(互补累积分布函数)性能仿真对比分析.本文中预留子载波的位置采用文献[13]中的数据进行仿真,令预留子载波个数为R =16,位置为
| $ \begin{array}{l} {Q_{16}} = \left\{ {5,16,25,40,65,84,102,108,131,140,} \right.\\ \left. {160,183,200,209,230,247} \right\}. \end{array} $ |
预留子载波个数为R=32,位置为
| $ \begin{array}{l} {Q_{32}} = \left\{ {5,11,16,23,25,33,40,54,65,71,84,} \right.\\ 90,102,105,108,125,131,138,140,147,160,172,\\ \left. {183,192,200,204,209,218,230,239,247,253} \right\}. \end{array} $ |
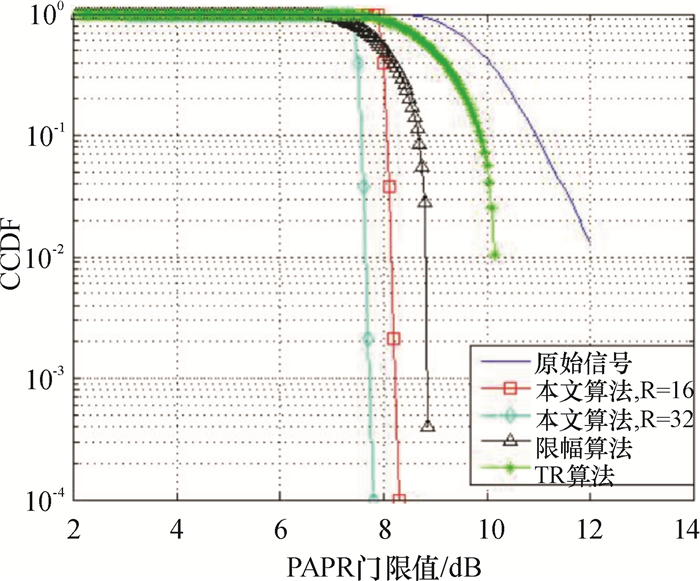
图 6显示了对10000个OFDM符号进行统计得到的各种算法PAPR的CCDF曲线,其中限幅算法参考文献[6],TR算法参考文献[13],在概率为10-2时,原始信号的PAPR为12.1dB,本文算法R=16时为8.1dB,增益为4.0dB,R=32时为7.8dB,增益为4.3dB.
|
图 6 CCDF曲线 Figure 6 CCDF curve |
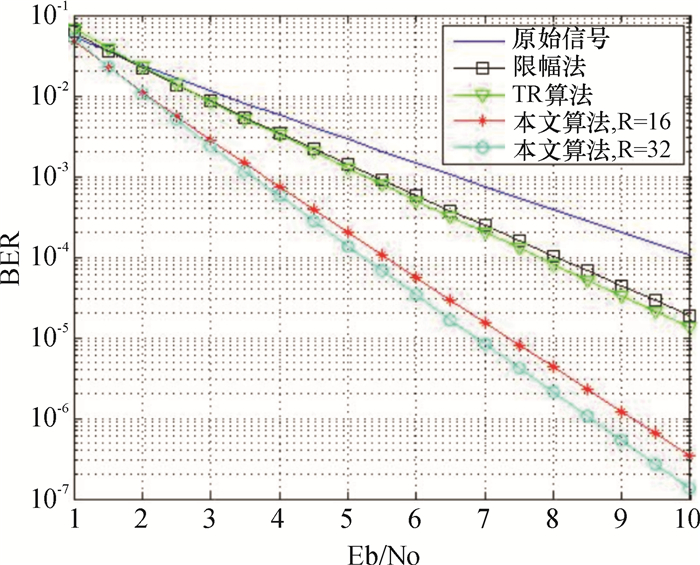
仿真3 图 7为与已有算法误比特率性能仿真对比分析,其中限幅算法参考文献[6],TR算法参考文献[13],可以看出本文的算法仿真效果明显优于其他算法.
|
图 7 误比特率曲线 Figure 7 BER curve |
本文提出了一种基于牛顿迭代法预留子载波功率分配的峰均比抑制方法,通过在时域对子载波进行限幅操作,然后在频域进行滤波操作得到预留子载波的初始状态,以系统信号失真功率比最大化为目标,预留子载波总功率受限为约束条件,采用牛顿迭代法求取最优预留子载波功率向量,可以有效降低PAPR.仿真结果表明,在总载波数256,预留载波数分别为16和32的条件下,峰均比抑制效果分别改善了4.0dB和4.3dB.
| [1] |
Tao J, Wu Y Y. An overview:peak-to-averge power ratio reduction techniques for OFDM signals[J].
IEEE Transactions On Broadcasting, 2008, 54(2): 257-268.
DOI: 10.1109/TBC.2008.915770. |
| [2] |
Han Seunghee, Lee Jaehong. An Overview of Peak-to-average power ratio reduction techniques for multicarrier transmission[J].
IEEE Wireless Communications, 2005, 12(2): 56-65.
DOI: 10.1109/MWC.2005.1421929. |
| [3] |
Huawei. PAPR reduction for TDD uplink OFDMA[S]. R1-050790, 3GPP TSG RAN WG1#42. London, UK. 29 Aug-2 sept, 2005.
|
| [4] |
Tellado J, Cioffi J M. Efficient algorithms for reducing PAR in multicarrier systems[J].
ISIT, 1998, 1(1): 191.
|
| [5] |
Dan L L, Xiao Y, Ni W. Improved peak cancellation for PAPR reduction in OFDM systems[J].
IEICE Transations on Communcations, 2010, E93-B(1): 198-202.
DOI: 10.1587/transcom.E93.B.198. |
| [6] |
Zhu X D, Pan W S. Simplifed approach to optimized iterative clipping and filtering for PAPR reduction of OFDM signals[J].
IEEE Transactions on Communications, 2013, 61(5): 1891-1901.
DOI: 10.1109/TCOMM.2013.021913.110867. |
| [7] |
Lim D W, Noh H S, No J S, et al. Near optimal PRT set selection algorithm for tone reservation in OFDM systems[J].
IEEE Transactions on Broadcasting, 2008, 54(3): 454-460.
DOI: 10.1109/TBC.2008.2000463. |
| [8] |
Chen J C, Li C P. Tone Reservation using near-optimal peak reduction tone set selection algorithm for PAPR reduction in OFDM systems[J].
IEEE Signal Processing Letters, 2010, 17(11): 933-936.
DOI: 10.1109/LSP.2010.2077278. |
| [9] |
Li H B, Jiang T. An improved tone reservation scheme with fast convergence for PAPR reduction in OFDM systems[J].
IEEE Transactions On Broadcasting, 2011, 57(4): 902-906.
DOI: 10.1109/TBC.2011.2169622. |
| [10] |
Gazor S, AliHemmatti R. Tone reservation for OFDM systems by maximizing signal-to-distortion ratio[J].
IEEE Transactions on Wireless Communications, 2012, 11(2): 762-770.
DOI: 10.1109/TWC.2011.121911.110454. |
| [11] |
Wu C Y, Lu Y. An improved clipping scheme based on TR for PAPR reduction in OFDM systems[C]//IEEE International Conference on Computer and Information Technology, Chengdu: IEEE, 2012, 1(1): 598-601.
|
| [12] |
Guel D, Palicot J. Transformation of any adding signal technique in tone reservation technique for PAPR mitigation thanks to frequency domain fitering[J].
International on Advances in Telecommunications, 2011, 4(1): 200-204.
|
| [13] |
Deumal M, Behravan A, Pijoan J L. On cubic metric reduction in OFDM system by tone reservation[J].
IEEE Transactions on Communications, 2011, 59(6): 1612-1620.
DOI: 10.1109/TCOMM.2011.042111.070613. |
| [14] |
Li Z Y, Zhang W Y. A new approach of clipping ratio estimation in clipped OFDM system[J].
Journal of University of Science and Technology of China, 2011, 41(11): 950-957.
|
| [15] |
Litsyn S. Peak power control in multicarrier communications[M]. UK: Cambridge University Press, 2007.
|
 2015, Vol. 32
2015, Vol. 32