数字体相关算法是在DIC技术基础上发展起来,计算物体内部三维位移场分布的一种算法[1-2].20世纪90年代B. K. Bay等[3-4]提出了数字体相关方法,并得到了广泛的关注,DVC需要的三维数据,大体上有两种来源:(1)计算机层析三维成像;(2)光学共焦显微三维成像.潘兵等[5-6]提出基于梯度的测量物体内部变形的DVC算法, 牛永强、樊雪松等[7-9]也做了大量有关方面的研究,J. Huang等[10]利用三维共焦荧光显微镜和DVC技术,测量加载前后随机嵌入微米荧光珠凝胶内部三维变形场分布[5].
目前计算三维位移场的方法较多[11].面临的问题就是如何在大量数据的前提下,做到最大程度提高位移计算精度和效率.在本文中,通过利用图像一阶灰度梯度来计算三维位移场,避免采用高阶的灰度梯度带来的麻烦,计算效率大幅提升,同时采用了在亚体素位置三元三次灰度插值法来提高位移计算精度的方法,做到精度和效率兼顾.
1 算法 1.1 数字体图像相关(DVC)模型数字体图像是由空间体像素构成的三维图像.当图像内部发生微小形变时,通过数字体图像相关法可求出体图像变形前后的三维位移场分布.其中变形前图像称为参考体图像,变形后图像称为目标体图像.从变形前后图像中各抽取一个小的体积块,变形前体积块称为参考体积元f(x, y, z),变形后的称为目标体积元g(x, y, z),如图 1所示.

|
图 1 数字体图像相关位移模型 Figure 1 The model of digital image correlation displacement |
测量体图像中某一个点p(x, y, z)的三维位移,通常是选择以该点为中心的一个包括(2N+1)×(2N+1)×(2N+1)个体素的体积块的位移,称为参考体积元,中心点坐标为p(x, y, z),目标体图像中的目标体积元,其中心点坐标为p'(x, y, z),f,g为图像的灰度,变形前后产生的三维位移为Δx,Δy,Δz.u,v,w代表整体素位移,Δu,Δv,Δw代表亚体素位移.体积元做微小移动近似刚体运动,变形前后同一点的灰度保持不变,f(p)=g(p').通过在目标体图像中逐体素的搜索与参考体积元最大相关的目标体积元,求出变形前后的位移.最大相关是相关函数C的最大值:
| $ C\left( {u, v, w} \right) = \frac{{\sum\limits_{x = - N}^N {\sum\limits_{y = - N}^N {\sum\limits_{z = - N}^N {\left[{f\left( {x, y, z} \right)-{f_m}} \right]} } } \cdot\left[{g\left( {x + u, y + v, z + w} \right)-{g_m}} \right]}}{{\sqrt {{{\sum\limits_{x = - N}^N {\sum\limits_{y = - N}^N {\sum\limits_{z = - N}^N {\left[{f\left( {x, y, z} \right)-{f_m}} \right]} } } }^2}} \cdot \sqrt {\sum\limits_{x = - N}^N {\sum\limits_{y = - N}^N {\sum\limits_{z = - N}^N {{{\left[{g\left( {x + u, y + v, z + w} \right)-{g_m}} \right]}^2}} } } } }}. $ | (1) |
式(1)中,fm和gm分别为参考和目标体积元的平均灰度,当C值越大越接近1,则表示相似程度越大,两个体积元的灰度分布越接近,得到的整体素位移u,v,w值会越精确,但此时只能搜索到整体素位移,属于粗测量,为达到更好效果,提高测量精度,所以引进亚体素的位移测量方法.
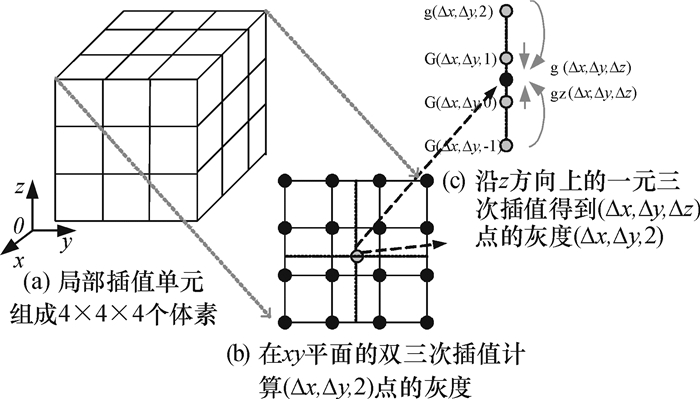
1.2 三元三次插值如果在上述体积元内有一点,它不在整体素点(x, y, z)位置,而是处于亚体素位置.于是每次逐步搜索的不再是整体素,而是亚像素.而体图像在亚像素位置并不存在灰度值,所以每次移动搜索前,要对亚体素所在的位置和该点灰度大小进行重建.本文采用高精度的三元三次灰度插值法,原理如图 2所示.图 2(a)表示所要插值点周围的一个单元组成,大小为4×4×4个体素.图 2(b)是从z轴上方向下看得到的xy平面图,每一个xy平面层都通过双三次插值得到一个亚体素构造点.图 2 (c)是经过双三次插值之后,每一层都有亚体素重建,通过一次一元三次插值,就能得到最终预插值点的亚体素重建.
|
图 2 亚体素重建中三元三次插值原理图 Figure 2 Schematic principle diagram of tricubic interpolation of subvoxel reconstruction |
双立方插值[12],称立方卷积插值法,是一种高精度插值方法,它考虑了待求点周围16个整像素点的灰度值,还考虑了这16个点在决定待求点灰度值时的权重,权重与这些整像素点离该点的距离密切相关,满足某一插值内核函数S(w), 表达式以及双三次插值公式如下:
| $ \begin{array}{l} \;\;\;\;S\left( w \right) = \\ \left\{ \begin{array}{l} {\left| w \right|^3} - 2{\left| w \right|^2} + 1, 0 < \left| w \right| \le 1;\\ - {\left| w \right|^3} - 5{\left| w \right|^2} - 8\left| w \right| + 4, 1 < \left| w \right| \le 2;\\ 0, 2 < \left| w \right|. \end{array} \right. \end{array} $ | (2) |
| $ f\left( {i + u, j + v} \right) = \mathit{\boldsymbol{ABC}}. $ | (3) |
其中,A, B, C均为矩阵,形式如下:
| $ \begin{array}{l} \mathit{\boldsymbol{A}}\left[{S\left( {1 + u} \right)\;\;\;\;S\left( u \right)\;\;\;\;S\left( {1-u} \right)\;\;\;\;S\left( {2-u} \right)} \right]\\ \mathit{\boldsymbol{B}} = \\ \left[{\begin{array}{*{20}{c}} {f\left( {i-1, j-2} \right)}&{f\left( {i, j-2} \right)}&{f\left( {i + 1, j - 2} \right)}&{{\rm{ }}f\left( {i + 2, j - 2} \right)}\\ {f\left( {i - 1, j - 1} \right)}&{f\left( {i, j - 1} \right)}&{f\left( {i + 1, j - 1} \right)}&{f\left( {i + 2, j - 1} \right)}\\ {f\left( {i - 1, j} \right)}&{f\left( {i, j} \right)\;\;\;\;}&{f\left( {i + 1, j} \right)\;\;\;}&{f\left( {i + 2, j} \right)}\\ {f\left( {i - 1, j + 1} \right)}&{{\rm{ }}f\left( {i, j + 1} \right)}&{f\left( {i + 1, j + 1} \right)}&{f\left( {i + 2, j + 1} \right)} \end{array}} \right]{\rm{ }}\\ \mathit{\boldsymbol{C}} = \\ {\left[{S\left( {1 + v} \right)\;\;\;\;S\left( v \right)\;\;\;\;S\left( {1-v} \right)\;\;\;\;S\left( {2-v} \right)} \right]^{\rm{T}}}. \end{array} $ | (4) |
其中f(i, j)表示源图像在该像素点的灰度值. u,v均为在[0, 1)区间的浮点数,分别表示待插值点与最临近像素点在水平和竖直方向的距离.通过图 2(b)中的双三次灰度插值,再构造一元三次插值函数把前面得到在z轴方向上的4个亚像素插值点灰度值代入公式,解出插值函数各个系数,从而得到欲插值点的灰度值.
1.3 基于梯度的亚体素位移算法在三维位移场测量中,体积元做微小位移u,v,w ,视为刚体运动,于是变形前后同一点的灰度值近似不变,此时有
| $ f\left( {x, y, z} \right) = g\left( {x + u + \Delta u, y + v + \Delta v, z + w + \Delta w} \right). $ | (5) |
将式(5)在g(x+u, y+v, z+w)处进行一阶泰勒展开,得到
| $ \begin{array}{l} \;\;\;\;\;\;\;g\left( {x + u + \Delta u, y + v + \Delta v, z + w + \Delta w} \right) = g\\ \left( {x + u, y + v, z + w} \right) + \Delta u \cdot {g_x} + \Delta v \cdot {g_y} + \Delta w \cdot {g_z}. \end{array} $ | (6) |
其中,gx,gy,gz分别为g(x+u, y+v, z+w)沿x, y, z方向的一阶灰度梯度,参考文献综合比较各种梯度算子,选用Barron算子计算灰度梯度,能得到比较高的精度.通过对式(6)采用最小二乘法原理并取得驻值,最终求得亚体素位移为Δ(Δu,Δv,Δw),被测体图像的三维位移场为整体素位移与亚像素位移之和,所以被测的整体素位移为Δx, Δy, Δz.
| $ \left\{ \begin{array}{l} \Delta x = u + \Delta u, \\ \Delta y = v + \Delta v, \\ \Delta z = w + \Delta w. \end{array} \right. $ | (7) |
首先由计算机模拟生成一幅3D散斑图作为变形前的散斑图[13],然后对于体图像中每一点,根据预设位移找到变形后其对应的位置,将该点的灰度值作为该位置处的灰度值.以高斯函数模拟散斑颗粒的光强分布,如图像背景光强均匀,则变形前后3D散斑体图像灰度分布函数如式(8),其中,s为空间散斑颗粒数目,R为空间散斑颗粒大小,是变参数,Ik0为第k个散斑颗粒中心的随机分布光强.(xk, yk, zk)和(x′k, y′k, z′k)分别是变形前后第k个空间散斑颗粒的中心位置.
| $ \left\{ \begin{array}{l} {I_r}\left( {x, y, z} \right) = \left\{ \begin{array}{l} \;\;\;\;\;\;\;\;{\left( {x - {x_k}} \right)^2} + {\left( {y - {y_k}} \right)^2} + \\ \sum\limits_{k = 1}^s {I_k^0{\rm{exp}}\left( { - \frac{{{{\left( {z - {z_k}} \right)}^2}}}{{{R^2}}}} \right), } \end{array} \right.\\ {I_o}\left( {x, y, z} \right) = \left\{ \begin{array}{l} \;\;\;\;\;\;\;\;{\left( {x - x{\prime _k}} \right)^2} + {\left( {y - y{\prime _k}} \right)^2} + \\ \sum\limits_{k = 1}^s {I_k^0{\rm{exp}}\left( { - \frac{{{{\left( {z - z{\prime _k}} \right)}^2}}}{{{R^2}}}} \right).} \end{array} \right. \end{array} \right. $ | (8) |
对参考体图像施加任意的平移公式为
| $ \left\{ \begin{array}{l} x{\prime _k} = {x_k} + u + \Delta u, \\ y{\prime _k} = {y_k} + v + \Delta v, \\ z{\prime _k} = {z_k} + w + \Delta w. \end{array} \right. $ | (9) |
式中u,v,w,Δx,Δy,Δz为预先设定的x, y和z方向整体像素位移分量和亚像素位移分量,据式(9)对参考图像施加任意平移,平移前图像如图 3所示.

|
图 3 参考体图像的3D图 Figure 3 3 D reference volume image |
通过计算机模拟仿真,模拟参数:模拟散斑颗粒数目s= 1000, 散斑图像大小为100voxel×100voxel×100voxel,刚体平移实验中, 设定x, y, z方向上的平移量分别为u= 3.28 voxel,v= 2.32voxel,w = 2.35voxel.生成参考体图像的3D散斑图,如图 3所示.刚体平移5组模拟参数分别为:(1)散斑半径R =2pixel,子体块边长ranr为5, 10, …50voxel.(2)散斑半径R =11pixel, 子体块边长ranr为5, 10, 15…50voxel.(3)颗粒半径R =2pixel,ranr为5, 8, 11…32voxel.(4)颗粒半径R =11 pixel,ranr为5, 8, 11…32voxel.采用不同散斑颗粒大小和不同边长的子体快来做刚体平移模拟实验,并且计算预设值与实验值之间的绝对误差、相对误差来比较散斑半径和子体块大小对精度的影响.(5)颗粒R的大小为2到11之间的随机数,子体块边长ranr为3, 5, 7, …, 21voxel,在每一个子体块边长中,采用10组随机位置的子体块,来得到预设值与实验值之差的标准误差以及总搜索的计算效率等,结果如图 4~7所示.

|
图 4 预设值与实验值的绝对误差 Figure 4 Absolute error between setting values and experinental values |

|
图 5 预设值与实验值的相对误差 Figure 5 Relative error between setting values and experinental values |

|
图 6 标准误差 Figure 6 Standard error |

|
图 7 计算效率 Figure 7 Computational efficiency |
本文介绍了测量物体内部三维矢量场的方法基本原理简单,在梯度法的基础上引入3次图像灰度插值的方法,计算精度高.从图 4~图 7可得出,基本达到预定效果,空间整体素与亚体素之和与预设值之间的绝对误差、相对误差都很小,计算精度较高.通过图 4和图 5可知,在同样大小子体块边长下,散斑颗粒半径R =2的性能比R =11的稍好,基本验证了算法的正确性;在图 6中,对于同一子体块边长下,散斑颗粒半径随机,从参考体图像中随机抽取10个位置的子体块来计算位移场与预设值之间误差的标准误差,标准误差比较小;同时,对于子体块体积大小的递增,每次搜索和进行相关计算的时间都会变得增加,如图 7所示,对于越大的子体块,搜索时所要进行灰度值相关性计算的就越多,插值点也相应增加,故而时间增加.
| [1] |
Franck C, Hong S, Maskarinec S A, et al. Three-dimensionalfull-field measurements of large deformations in soft materials using confocal microscopy and digital volume correlation[J].
Experimental Mechanics, 2007, 47(3): 427-438.
DOI: 10.1007/s11340-007-9037-9. |
| [2] |
Gates M, Lambros J, Heath M. Towards high performance digital volume correlation[J].
Experimental Mechanics, 2011, 51(4): 491-507.
DOI: 10.1007/s11340-010-9445-0. |
| [3] |
Bay B K, Smith T S, Fyhrie D P, et al. Digital volume correlation: Three-dimensional strain mapping using X-ray tomography[J].
Experimental Mechanics, 1999, 39(3): 217-226.
DOI: 10.1007/BF02323555. |
| [4] |
Bay B K. Methods and applications of digital volume correlation[J].
Journal of Strain Analysis for Engineering Design, 2008, 43(8): 745-760.
DOI: 10.1243/03093247JSA436. |
| [5] |
潘兵, 吴大方, 谢惠民, 等. 基于梯度的数字体图像相关方法测量物体内部变形[J].
光学学报, 2011, 31(6): 120-126.
Pan B, Wu D F, Xie H M, et al. Spatial-gradient-based digital volume correlation technique for internal deformation measurement[J]. Acta Optica Sinica, 2011, 31(6): 120-126. |
| [6] |
潘兵, 吴大方, 郭保桥. 数字体图像相关方法中基于迭代最小二乘法的物体内部变形测量[J].
实验力学, 2011, 26(6): 665-673.
Pan B, Wu D F, Guo B Q. Digital volume image correlation by using iterative Least-Squares for Internal deformation measurement of an object[J]. Journal of Experimental Mechanics, 2011, 26(6): 665-673. |
| [7] |
樊雪松. 数字散斑相关方法的研究[D]. 天津: 天津大学机械工程学院, 2004.
http://cdmd.cnki.com.cn/Article/CDMD-10056-2004075741.htm
|
| [8] |
牛永强. 物体内部三维位移场测量算法研究[D]. 合肥: 中国科学技术大学计算机科学与技术学院, 2010.
http://cdmd.cnki.com.cn/Article/CDMD-10358-2010210779.htm
|
| [9] |
夏桂锁. 数字图像相关测量方法的理论及应用研究[D]. 天津: 天津大学机械工程学院, 2003.
http://cdmd.cnki.com.cn/Article/CDMD-10056-2004074922.htm
|
| [10] |
Huang J, Pan X, Li S, et al. A digital volume correlation technique for 3D deformation measurements of soft gels[J].
Inter-national Journal of Applied Mechanics, 2011, 3(2): 335-354.
DOI: 10.1142/S1758825111001019. |
| [11] |
汪敏, 胡小方, 伍小平. 物体内部三维位移场分析的数字图像相关方法[J].
物理学报, 2006, 55(10): 5135-5139.
Wang M, Hu X F, Wu X P. Digital image correlation method for the analysis of 3D internal displacement field in object[J]. Acta Physica Sinica, 2006, 55(10): 5135-5139. |
| [12] |
王会鹏, 周利莉, 张杰. 一种基于区域的双三次图像插值算法[J].
计算机工程, 2010, 36(19): 216-218.
Wang H P, Zhou L L, Zhang J. Region-based bicubic image interpolation algorithm[J]. Computer Engineering, 2010, 36(19): 216-218. DOI: 10.3969/j.issn.1000-3428.2010.19.076. |
| [13] |
Zhou P, Goodson K E. Subpixel displacement and deformation gradient measurement using digital image/speckle correlation[J].
Optical Engineering, 2001, 40(8): 1613-1620.
DOI: 10.1117/1.1387992. |
 2015, Vol. 32
2015, Vol. 32