多铁材料,尤其是同时具有铁电与铁磁性质的多铁材料,近些年一直是自旋设备研究中的热点[1-2].多铁材料的研究对于自旋物理学的基础研究具有重要意义,并且可以应用于存储器、传感器等[3-4].然而由于多铁性的形成需要特殊的电子结构,单相多铁材料在自然界中很难得到[5-6].钙钛矿相BiFeO3(缩写为BF)是多铁材料的典型代表,它同时具有很高的铁电居里温度(TC~1 100 K)和较高的反铁磁聂耳温度(TN~643 K)[7].目前已经有很多研究致力于开发BF基材料的多铁性及磁电耦合效应[8].然而,单相BF具有较大的漏电流,较小的抗疲劳特性,并且难以制备,这些大大限制了材料的应用.通过其他离子掺杂或者与其他物质复合,可以有效地改善BF的多铁性能[9-10].其中,Ti离子取代Fe离子是一种有效的方法:一方面,Ti离子相对于Fe离子具有较小的半径,易于进入晶格对Fe离子进行部分取代;另一方面,这种高价取代能有效地降低BF中氧空位的浓度,抑制铁氧化物等杂相生成.
BaTiO3(缩写为BT)具有高介电常数、高铁电极化等优良的电学性质,目前已被广泛应用于电子材料行业.研究发现,BF-BT复合材料能有效改善BF的结构稳定性、电学、磁学性能[11].此外,通过适当的Zr掺杂,Ba(Zr0.06Ti0.94)O3(缩写为BZT6)陶瓷表现出比BT更加优异的电学性能[12-13].因此,本实验选用电学性能更加优异的BZT6作为研究对象,通过与BF进行复合,制备出BZT6-BF系列陶瓷,并研究其相结构、介电、铁电和压电性能.
1 实验 1.1 样品的制备Ba(Zr0.06Ti0.94)O3-x%BiFeO3 (x=0.2, 0.4, 0.6, 0.8, 缩写为BZT6-x%BF)复合陶瓷通过传统高温固相法分两步制备而成.首先分别制备BZT6与BF的粉末样品:分别采用BaCO3(99%), ZrO2(99%), TiO2 (99%)和Fe2O3(85%), Bi2O3(99%)为原料,将称量好的氧化物按照比例混合后在行星球磨机中球磨12 h, 筛分后干燥,分别在1200 ℃与800 ℃预烧2 h.再将预烧后的BZT6和BF粉末按照复合陶瓷的比例进行混合、研磨,经聚乙烯醇(PVA)造粒、压片成型、排胶退火后,在1 350 ℃烧结2 h得到复合陶瓷样品.
1.2 样品表征采用X射线衍射仪(Pgeneral XD-2) CuKα射线源对样品进行了物相分析.为了测量电学性能,对样品两面进行抛光镀导电银浆,经650 ℃退火后得到了银电极.样品的介电常数-温度图谱采用介电谱仪(Agilent E4980A)进行表征;电滞回线由铁电分析仪(Radiant Technolies’ Precision premier Ⅱ)测量,采用Sawyer-Tower回路,输入信号为频率100 Hz的正弦信号;压电系数d33采用准静态d33/d31测量仪(中科院声学研究所ZJ-6A型)完成测量.
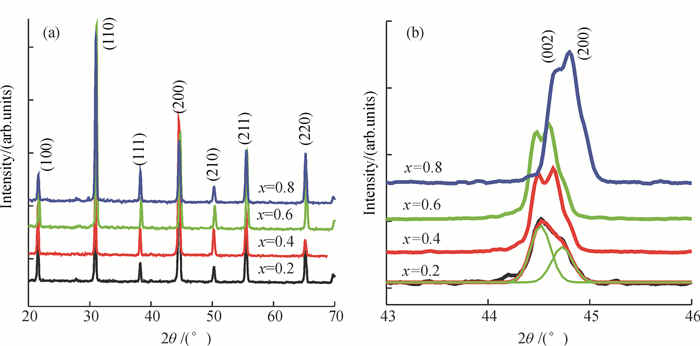
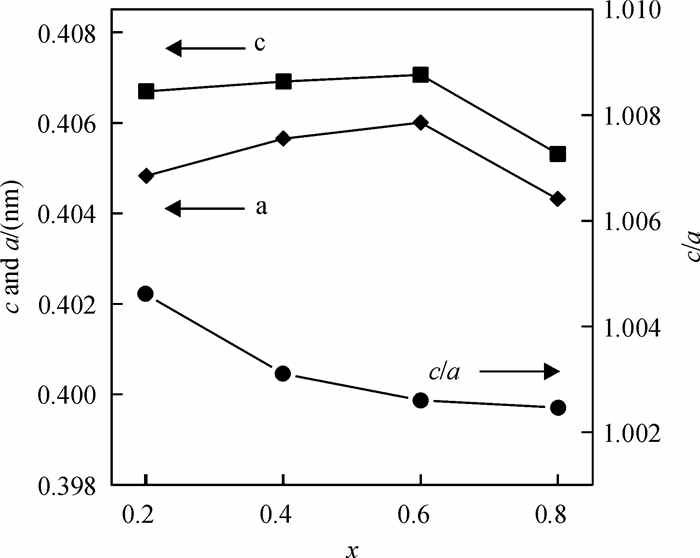
2 结果与讨论 2.1 样品的结构表征图 1中(a)是不同成分BZT6-x%BF复合陶瓷的XRD图谱.从图中可以看出,所有样品均显示出典型的钙钛矿四方相结构,并且没有杂相生成[14].峰的强度很高,说明BZT6与BF形成了很好的复合.将XRD图谱2θ从44°到46°的范围进行局部放大,如图 1中(b)所示,复合陶瓷的(002)与(200)峰发生了明显的分裂,并且随着BF含量的增加,峰的分裂逐渐变小,(200)峰越来越明显.这说明样品的晶格常数随着BF的含量发生了相应的变化.根据四方晶格的面间距计算公式及布拉格衍射公式,算得四方相的晶格常数变化,见图 2.从图 2中可以看出,晶格常数c与a开始随着BF含量的增加增大,之后在x达到0.8时明显减小,而c/a的比值始终呈现微小的逐渐下降的趋势.说明随着BF含量的增加,复合陶瓷的对称性在逐渐增大.晶格的变化与离子的分布直接相关,由于A位Ba2+、Bi3+,B位Fe3+、Zr4+、Ti4+具有不同的离子半径、化合价态和结合能,样品成分的变化势必会对晶体结构产生一定的影响.
|
图 1 BZT6-x%BF复合陶瓷的XRD图谱和2θ从44°~46°的局部放大图 Figure 1 XRD patterns and magnified view within the 44° to 46° region for BZT6-x%BF composite ceramics |
|
图 2 BZT6-x%BF复合陶瓷晶格常数c, a以及两者比值c/a随变量x变化图 Figure 2 Lattice parameters c, a and c/a of the BZT6-x%BF composite ceramics with various x |
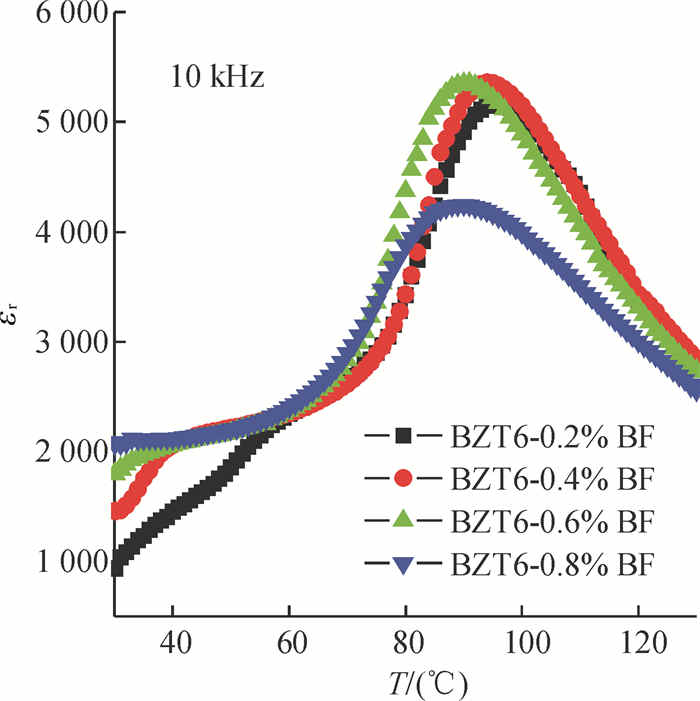
图 3是BZT6-x%BF复合陶瓷在10 kHz下介电常数与温度关系图.从图 3中可以看出,在测量的温度范围内介电常数只存在一个峰值,这个峰对应于复合陶瓷的相变过程,并且峰位随着BF含量而变化,这说明BF已经扩散到BZT6的晶格中,导致晶格畸变,从而影响样品的相变温度.另外,随着陶瓷中BF成分的变化,介电常数大小也随之变化.
|
图 3 BZT6-x%BF复合陶瓷在10 kHz下介电常数-温度关系 Figure 3 Dielectric permittivity εr versus temperature curves of BZT6-x%BF composite ceramics measured at 10 kHz |
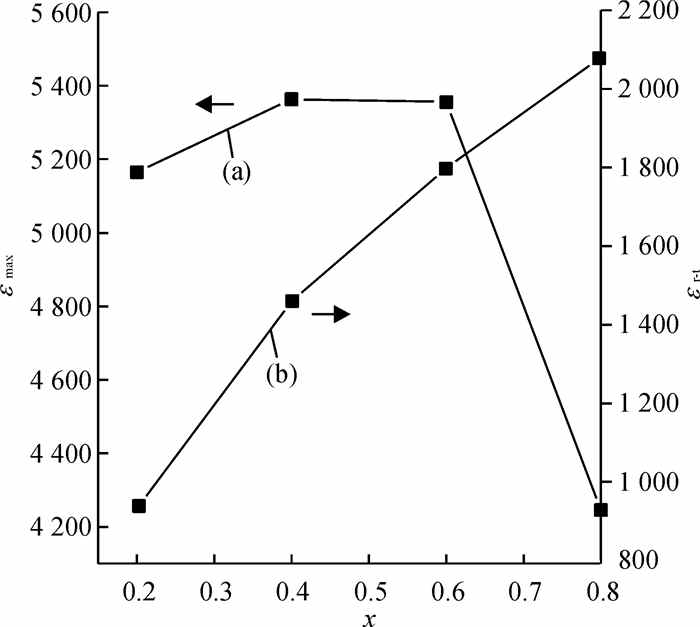
将不同样品的最高介电常数和室温介电常数分别提取,列于图 4,可以明显看出两者随BF含量的变化关系.随着BF含量的增加,样品的最高介电常数先呈现一个微小的上升趋势,然后急剧下降,见图 4中曲线(a).这和BZT6与BF本身的介电常数相关,BZT6是一种良好的电介质,而BF由于较大漏电流的存在,介电常数较小.在BF含量较低时,略小于Fe离子半径的Ti离子能很容易地进入Fe-O八面体, 取代较低价的Fe,从而有效抑制氧空位的生成;而当BF含量达到一定程度时,样品本身的漏电流缺陷就会有所显现,从而造成最大介电常数的降低.另外,BF的含量还会影响晶粒的大小,从而间接影响陶瓷的介电性质.
|
图 4 BZT6-x%BF复合陶瓷在10 kHz下的最高介电常数εmax(a)、室温介电常数εr-t(b)与BF含量的关系 Figure 4 (a) Maximum dielectric permittivity and (b) room temperature dielectric permittivity of BZT6-x%BF composite ceramics measured at 10 kHz with various BF concentrations |
然而,复合陶瓷的室温介电性能产生了规律性的变化:根据室温介电常数的变化曲线图 4中曲线(b),BF含量的增加有效地增加了复合陶瓷的室温介电性,这对于复合陶瓷的室温应用具有一定价值.本实验中BZT6-x%BF,即Ba(Zr0.06Ti0.94)O3-x%BiFeO3,比之前报道的BiFeO3-Ba(Zr0.6Ti0.4)O3介电常数高出很多[15],这主要归功于Ba(Zr0.06Ti0.94)O3优良的介电性能.
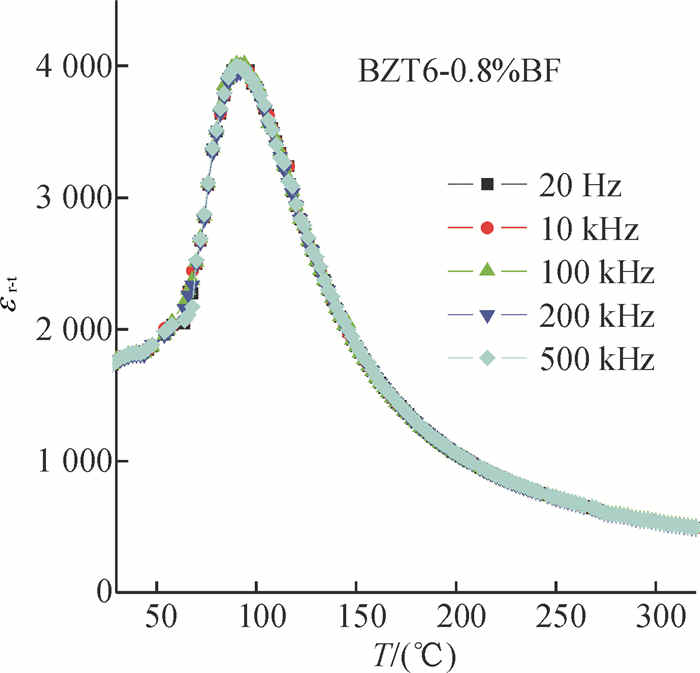
另一方面,介电-温度图(见图 3)中相的转变并没有引起一个尖锐的相变峰,这说明相变没有随着温度发生骤变,样品存在铁电弛豫现象.根据成分起伏理论,对化学组成复杂并在同一晶位上有多种离子共同占位的钙钛矿铁电体,容易出现化学组成和晶体结构在纳米尺度上的不均匀,导致材料出现铁电弛豫性特征[16].本实验中除了主晶格的相变,BF渗入到BZT6晶格的程度也会随着温度的升高逐渐变化,从而引起局部晶格的缓慢变化,造成弛豫现象.为了验证频率是否对复合陶瓷的介电性能产生影响,本实验采用不同频率测量了复合陶瓷BZT6-0.8%BF的介电常数与温度关系,如图 5所示.笔者发现,测量频率的变化并没有对样品的介电图谱产生影响.
|
图 5 不同频率下BZT6-0.8%BF的介电常数与温度关系图 Figure 5 Dielectric permittivity versus temperature curves of BZT6-0.8%BF measured at various frequencies |
一般铁电体的相变遵循居里-外斯定律[17],
| $ \frac{1}{{{\varepsilon _{\rm{r}}}}} = \frac{{T - {T_0}}}{C}\ \ \ (T > {T_0}), $ | (1) |
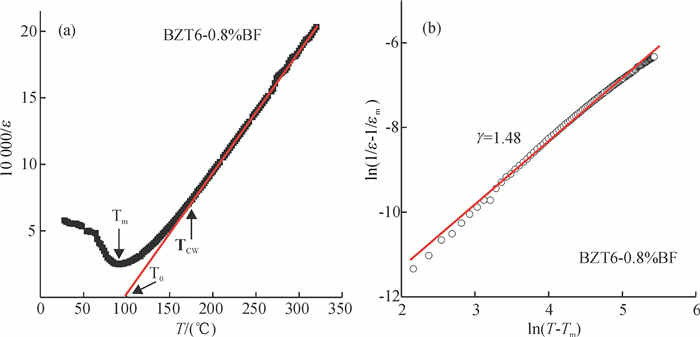
式中T0是居里外斯温度,C是居里外斯常数.笔者将陶瓷在10 kHz下的介电图谱进行居里外斯拟合,如图 6(a)所示,发现样品的介电常数与温度并不完全符合居里-外斯定律,而是在温度高于TCW=175.6之后才会符合类似的直线关系.这个临界温度TCW远高于介电系数最大值对应的温度Tm以及居里温度T0,说明样品具有明显的弥散相变行为.这种行为可以用经验修正的居里-外斯定律[18]描述:
| $ \frac{1}{\varepsilon } - \frac{1}{{{\varepsilon _{\rm{m}}}}} = \frac{{{{(T - {T_{\rm{m}}})}^\gamma }}}{{{C_1}}}\;\;\;\left( {1 \le \gamma \le 2} \right). $ | (2) |
|
图 6 BZT6-0.8%BF复合陶瓷在10 kHz下的10 000/ε与T关系图(a),直线用来拟合居里-外斯定律以及ln(1/εr-1/εm)与ln(T-Tm)关系图(b),直线用来拟合修正的居里-外斯定律 Figure 6 10 000/ε versus T curve (a) and ln(1/εr-1/εm) versus ln(T-Tm) curve (b) of BZT6-0.8%BF composite ceramics, the straight lines were used to fit the Curie-Weiss and modified Curie-Weiss law, respectively |
其中γ和C1均是常数.γ为弥散系数,可以用来表征相变的性质.当γ=1时,样品遵循居里外斯相变,当γ=2时,表示样品完全遵循弥散相转变.图 6(b)是ln(1/εr-1/εm)与ln(T-Tm)关系图,用来拟合修正的居里-外斯定律.计算得到样品的弥散系数γ=1.48 > 1,表明两种相变在样品中同时存在.较小的弥散系数值(γ < 1.5),表明复合陶瓷的化学组成和结晶相对均匀,相变弥散程度较低.
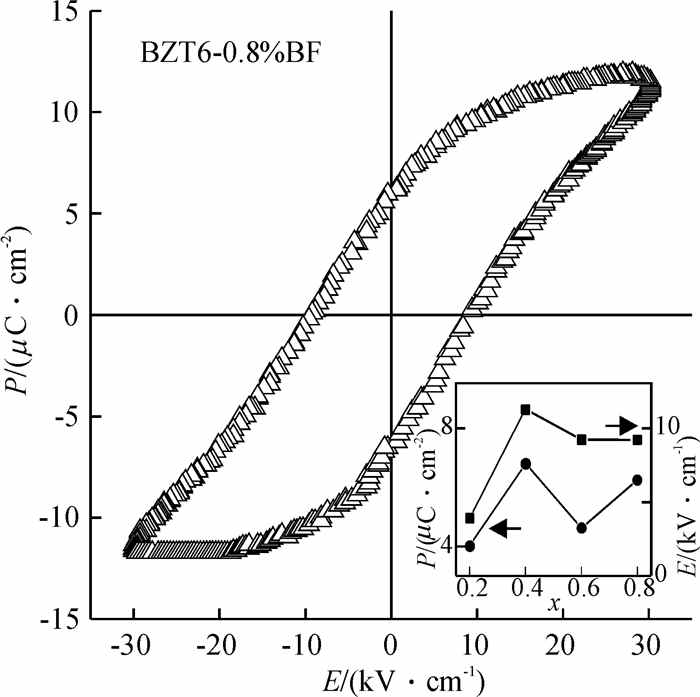
2.3 样品的铁电与压电性能图 7是BZT6-x%BF复合陶瓷的室温电滞回线图谱.其中的插图为不同BF含量复合陶瓷的铁电剩余极化(Pr)与矫顽场(Ec).从插图可以看出,不同BF含量的复合陶瓷均具有良好的铁电性质,表现出较高的剩余极化与较低的矫顽场,这非常有利于材料的铁电应用[19].其中x=0.8时,复合陶瓷铁电性能最为优异.从图中可以看出,室温BZT6-0.8%BF复合陶瓷电滞回线显示出较高的矩形度,同时拥有较大剩余极化(Pr=6.245)与较小的矫顽场(Ec=9.215).BZT6-x%BF复合陶瓷这种室温铁电性可能与复合陶瓷较小的漏电流特性相关.如前所述,BF本身具有较大的漏电流,致使材料的铁电性能大大削弱,但与BZT6复合之后,一部分高价态的Ti离子就会取代价态较低的Fe离子,从而减小材料的漏电流,增强材料的铁电性.这与图 4曲线(b)中的室温介电性能相对应.室温状态下,较高的BF含量可以降低材料的漏电流,增强材料的介电性能.然而由于铁电性的影响因素复杂,除去物质的种类、离子价态、晶体结构、晶粒大小、以及微观缺陷等等都会影响材料的铁电性能,笔者并不能明确指出具体成因.
|
图 7 BZT6-0.8%BF复合陶瓷的室温电滞回线图谱.插图为不同BF含量BZT6-x%BF复合陶瓷的铁电剩余极化(Pr)与矫顽场(Ec)示意图 Figure 7 Room temperature hysteresis loop of the BZT6-0.8%BF composite ceramic. The inset shows the residual polarization (Pr) and coercive field (Ec) of BZT6-x%BF composite ceramics with various BF concentrations |
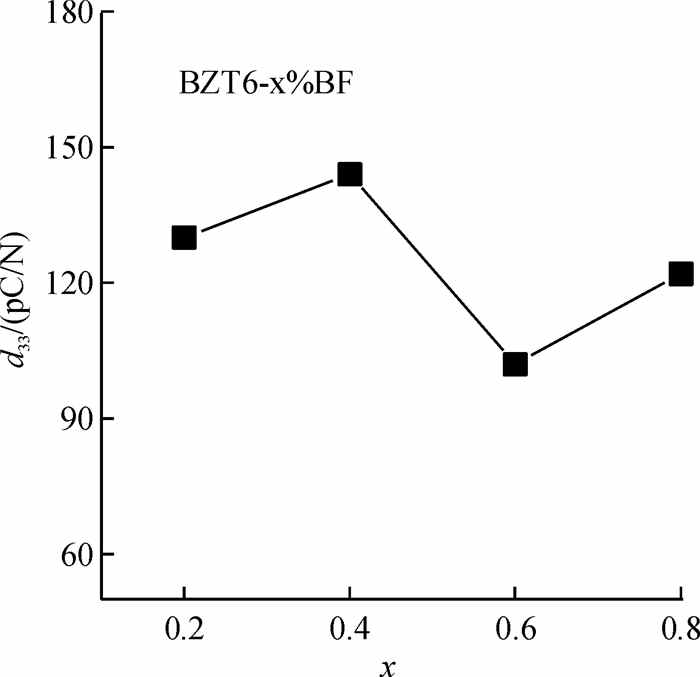
图 8是BZT6-x%BF复合陶瓷的压电系数d33与BF含量的关系图.从图中可以看出,所有的材料均显示出一定的压电性质,最大压电系数出现在x=0.4时,此时复合陶瓷的压电系数d33=144 pC/N.尽管BZT6-x%BF复合陶瓷的压电系数并不是特别高,但相比于一般铁电材料,尤其是BF陶瓷[20],其压电效应已经非常明显.此外,通过比较图 8与图 7中的插图,还注意到,复合陶瓷的压电系数与铁电极化呈现出了相同的变化趋势.这是因为不同的BF成分导致复合陶瓷的极化状态不同,从而间接影响到陶瓷的铁电极化与压电系数.
|
图 8 BZT6-x%BF复合陶瓷的压电系数d33与BF含量关系 Figure 8 Relationship between the piezoelectric coefficient d33 and BF concentration of BZT6-x%BF composite ceramics |
采用高温固相法制备出BZT6-x%BF (x=0.2, 0.4, 0.6, 0.8)系列复合陶瓷,并研究了其相结构、介电、铁电和压电性质.XRD结果表明,所有样品均呈现典型的钙钛矿四方相结构,无杂相生成,并且样品的晶格常数随着BF的含量发生了一定变化.介电-温度图谱表明BF已经扩散到BZT6的晶格中,导致晶格畸变,从而影响了样品的相变温度.随着BF成分的变化,陶瓷的介电常数大小也受到影响,室温介电常数随着BF含量的增加不断增大.所有样品均具有较宽的相变峰,表明复合陶瓷中存在弥散相变.通过计算得到BZT6-0.8%BF样品的弥散系数γ=1.48,表明两种相变在样品中同时存在,复合陶瓷的化学组成和晶体结构相对均匀,相变弥散程度较低.所有样品均显示出明显的铁电与压电特性,并且随着BF含量变化,两者呈现出相同的变化趋势.这与复合陶瓷的极化状态密切相关.
| [1] |
Eerenstein W, Mathur N D, Scott J F. Multiferroic and magnetoelectric materials[J].
Nature, 2006, 442(7104): 759-765.
DOI: 10.1038/nature05023. |
| [2] |
Sergienko A, Dagotto E. Role of the Dzyaloshinskii-Moriya interaction in multiferroic perovskites[J].
Phys Rev B, 2006, 73(9): 094434.
DOI: 10.1103/PhysRevB.73.094434. |
| [3] |
Hur N, Park S, Sharma P A, et al. Electric polarization reversal and memory in a multiferroic material induced by magnetic fields[J].
Nature, 2004, 429(6990): 392-395.
DOI: 10.1038/nature02572. |
| [4] |
Li B, Wang C Q, Zhang W, et al. Fabrication of multiferroic Ba0.7Sr0.3TiO3-Ni0.8Zn0.2Fe2O4 composite nanofibers by electrospinning[J].
Mater Lett, 2013, 91: 55-58.
DOI: 10.1016/j.matlet.2012.09.060. |
| [5] |
Hill N A. Why are there so few magnetic ferroelectrics?[J].
J Phys Chem B, 2000, 104(29): 6694-6709.
DOI: 10.1021/jp000114x. |
| [6] |
He S M, Liu G L, Xu J, et al. Magnetodielectric effect in lead-free multiferroic CoFe2O4/K0.5Na0.5NbO3 bilayers[J].
Mater Lett, 2012, 89: 159-162.
DOI: 10.1016/j.matlet.2012.08.096. |
| [7] |
Zhao T, Scholl A, Zavaliche F, et al. Electrical control of antiferromagnetic domains in multiferroic BiFeO3 films at room temperature[J].
Nat Mater, 2006, 5(10): 823-829.
DOI: 10.1038/nmat1731. |
| [8] |
Chu Y H, Martin L W, Holcomb M B, et al. Electric-field control of local ferromagnetism using a magnetoelectric multiferroic[J].
Nat Mater, 2008, 7(6): 478-482.
DOI: 10.1038/nmat2184. |
| [9] |
Schiemer J, Withers R L, Carpenter M A, et al. Temperature-dependent electrical, elastic and magnetic properties of sol-gel synthesized Bi0.9Ln0.1FeO3 (Ln=Nd, Sm)[J].
J Phys Condens Matter, 2012, 24(12): 125901.
DOI: 10.1088/0953-8984/24/12/125901. |
| [10] |
Ma C B, Tang X G, Chen D G, et al. Reduced leakage current and enhanced magnetic properties of (Bi, Nd)FeO3 thin films grown on (Ba, Sr)TiO3 bottom layer[J].
Funct Mater Lett, 2012, 5(3): 1250032.
DOI: 10.1142/S1793604712500324. |
| [11] |
Sahni M, Kumar N, Singh S, et al. Influence of Mn doping on structural, electrical and magnetic properties of (0.90)BiFeO3-(0.10)BaTiO3 composite[J].
J Mater Sci Mater Electron, In press, .
DOI: 10.1007/s10854-014-1859-5. |
| [12] |
Kuang S J, Tang X G, Wu J B, et al. Pinning effects on the dielectric and ferroelectric properties of Mn-doped Ba(Zr0.06Ti0.94)O3 ceramics[J].
Mater Sci Forum, 2011, 687: 354-358.
DOI: 10.4028/www.scientific.net/MSF.687. |
| [13] |
杨中服, 唐新桂. 纳米晶Ba(Zr0.2Ti0.8)O3薄膜的外延生长与介电特性[J].
广东工业大学学报, 2008, 25(1): 11-14.
Yang Z F, Tang X G. Dielectric properties of nanocrystalline Ba(Zr0.2Ti0.8)O3 thin films epitaxially grown on (001) SrTiO3:Nb single crystal substrate[J]. Journal of Guangdong University of Technology, 2008, 25(1): 11-14. |
| [14] |
Ma C B, Tang X G, Kuang S J. Effect of (Bi0.5Na0.5)TiO3 compositions on the structure, dielectric and ferroelectric properties of BaTiO3 ceramics[J].
Scientific Journal of Physical Science, 2012, 2(3): 87-91.
|
| [15] |
Choudhary R N P, Perez K, Bhattacharya P, et al. Structural and dielectric properties of mechanochemically synthesized BiFeO3-Ba(Zr0.6Ti0.4)O3 solid solutions[J].
Mater Chem Phys, 2007, 105(2-3): 286-292.
DOI: 10.1016/j.matchemphys.2007.04.066. |
| [16] |
Smolensky G. Ferroelectrics with diffuse phase transition[J].
Ferroelectrics, 1984, 53(1): 129-135.
DOI: 10.1080/00150198408245041. |
| [17] |
Tang X G, Wang X X, Chew K H, et al. Relaxor behavior of (Ba, Sr)(Zr, Ti)O3 ferroelectric ceramics[J].
Solid State Commun, 2005, 136(2): 89-93.
DOI: 10.1016/j.ssc.2005.06.034. |
| [18] |
Martirena H T, Burfoot J C. Grain-size and pressure effects on the dielectric and piezoelectric properties of hot-pressed PZT-5[J].
Ferroelectrics, 1974, 7(1): 151-152.
DOI: 10.1080/00150197408237979. |
| [19] |
丘翠环, 陈丽, 李智强. 铁电和铁磁微分回线谱分析[J].
广东工业大学学报, 2002, 19(2): 69-72.
Qiu C H, Chen L, Li Z Q. Spectrum analysis on the differential hysteresis loops of ferroelectric and ferromagnetism[J]. Journal of Guangdong University of Technology, 2002, 19(2): 69-72. |
| [20] |
Rojac T, Bencan A, Drazic G, et al. Piezoelectric nonlinearity and frequency dispersion of the direct piezoelectric response of BiFeO3 ceramics[J].
J Appl Phys, 2012, 112(6): 064114.
DOI: 10.1063/1.4754315. |
 2014, Vol. 31
2014, Vol. 31

