在渗流、扩散、热传导等领域中经常会遇到求解抛物型方程的问题, 对于一维抛物型方程的研究, 其模型为如下初边值问题
| $ \left\{ \begin{array}{l} \frac{{\partial u}}{{\partial t}} = a\frac{{{\partial ^2}u}}{{\partial {x^2}}},0 \le x \le L,0 \le t \le T,a > 0,\\ u\left( {x,0} \right) = f\left( x \right),0 \le x \le L,\\ u\left( {0,t} \right) = u\left( {\pi ,t} \right) = 0,0 \le t \le T. \end{array} \right. $ | (1) |
在解上述问题的线性差分格式中, 已有较多的研究[1-14].张莉[6]给出了一个两层六点半显格式, 其截断误差为O(τ2+h3), 稳定性条件为0 < r < 1.17.陈泽龙[8]给出了一个两层七点半显式格式, 其截断误差为O(τ2+h4), 稳定性条件为0 < r≤0.4647.基于此, 本文用待定系数法构造了一个两层八点的高精度隐式差分格式, 截断误差为O(τ3+h5), 稳定性条件是0.001 < r < 0.231或0.236 < r < 0.772.
1 格式的构造设时间步长为τ, 空间步长为
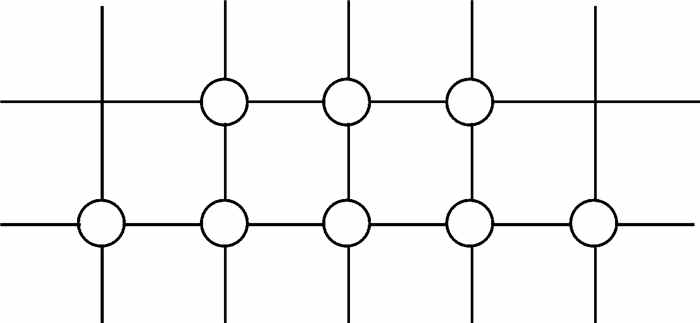
|
图 1 差分格式节点示意图 Figure 1 Difference scheme node schemes |
当问题(1)的解充分光滑时, 有如下关系式:
| $ \frac{{{\partial ^{m + n}}u}}{{\partial {x^m}\partial {t^n}}} = {a^n}\frac{{{\partial ^{m + 2n}}u}}{{\partial {x^{m + 2n}}}}, $ | (2) |
其中m、n为非负整数.将8个节点上u的值在节点(jh, nτ)处作Taylor展开, 得
| $ \begin{array}{l} u_{j - 2}^n = u_j^n - 2h\frac{{\partial u}}{{\partial x}} + \frac{{{{\left( {2h} \right)}^2}}}{{2!}}\frac{{{\partial ^2}u}}{{\partial {x^2}}} - \frac{{{{\left( {2h} \right)}^3}}}{{3!}}\frac{{{\partial ^3}u}}{{\partial {x^3}}} + \\ \frac{{{{\left( {2h} \right)}^4}}}{{4!}}\frac{{{\partial ^4}u}}{{\partial {x^4}}} - \frac{{{{\left( {2h} \right)}^5}}}{{5!}}\frac{{{\partial ^5}u}}{{\partial {x^5}}} + \frac{{{{\left( {2h} \right)}^6}}}{{6!}}\frac{{{\partial ^6}u}}{{\partial {x^6}}} + O\left( {{h^7}} \right), \end{array} $ | (3) |
| $ \begin{array}{l} u_{j - 1}^n = u_j^n - h\frac{{\partial u}}{{\partial x}} + \frac{{{h^2}}}{{2!}}\frac{{{\partial ^2}u}}{{\partial {x^2}}} - \frac{{{h^3}}}{{3!}}\frac{{{\partial ^3}u}}{{\partial {x^3}}} + \frac{{{h^4}}}{{4!}}\frac{{{\partial ^4}u}}{{\partial {x^4}}} - \\ \frac{{{h^5}}}{{5!}}\frac{{{\partial ^5}u}}{{\partial {x^5}}} + \frac{{{h^6}}}{{6!}}\frac{{{\partial ^6}u}}{{\partial {x^6}}} + O\left( {{h^7}} \right), \end{array} $ | (4) |
| $ \begin{array}{l} u_{j + 1}^n = u_j^n + h\frac{{\partial u}}{{\partial x}} + \frac{{{h^2}}}{{2!}}\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{h^3}}}{{3!}}\frac{{{\partial ^3}u}}{{\partial {x^3}}} + \frac{{{h^4}}}{{4!}}\frac{{{\partial ^4}u}}{{\partial {x^4}}} + \\ \frac{{{h^5}}}{{5!}}\frac{{{\partial ^5}u}}{{\partial {x^5}}} + \frac{{{h^6}}}{{6!}}\frac{{{\partial ^6}u}}{{\partial {x^6}}} + O\left( {{h^7}} \right), \end{array} $ | (5) |
| $ \begin{array}{l} u_{j + 2}^n = u_j^n + 2h\frac{{\partial u}}{{\partial x}} + \frac{{{{\left( {2h} \right)}^2}}}{{2!}}\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{{\left( {2h} \right)}^3}}}{{3!}}\frac{{{\partial ^3}u}}{{\partial {x^3}}} + \\ \frac{{{{\left( {2h} \right)}^4}}}{{4!}}\frac{{{\partial ^4}u}}{{\partial {x^4}}} + \frac{{{{\left( {2h} \right)}^5}}}{{5!}}\frac{{{\partial ^5}u}}{{\partial {x^5}}} + \frac{{{{\left( {2h} \right)}^6}}}{{6!}}\frac{{{\partial ^6}u}}{{\partial {x^6}}} + O\left( {{h^7}} \right), \end{array} $ | (6) |
| $ \begin{array}{l} u_{j - 1}^{n + 1} = u_j^n + \left( { - h\frac{{\partial u}}{{\partial x}} + \tau \frac{{\partial u}}{{\partial t}}} \right) + \frac{1}{{2!}}\left( {{h^2}\frac{{{\partial ^2}u}}{{\partial {x^2}}} - } \right.\\ \left. {2h\tau a\frac{{{\partial ^3}u}}{{\partial {x^3}}} + {\tau ^2}{a^2}\frac{{{\partial ^4}u}}{{\partial {x^4}}}} \right) + \frac{1}{{3!}}\left( { - {h^3}\frac{{{\partial ^3}u}}{{\partial {x^3}}} + 3{h^2}\tau a\frac{{{\partial ^4}u}}{{\partial {x^4}}} - } \right.\\ \left. {3h{\tau ^2}{a^2}\frac{{{\partial ^5}u}}{{\partial {x^5}}} + {\tau ^3}{a^3}\frac{{{\partial ^6}u}}{{\partial {x^6}}}} \right) + \frac{1}{{4!}}\left( {{h^4}\frac{{{\partial ^4}u}}{{\partial {x^4}}} - 4{h^3}\tau a\frac{{{\partial ^5}u}}{{\partial {x^5}}} + } \right.\\ \left. {6{h^2}{\tau ^2}{a^2}\frac{{{\partial ^6}u}}{{\partial {x^6}}} - 4h{\tau ^3}{a^3}\frac{{{\partial ^7}u}}{{\partial {x^7}}}} \right) + \frac{1}{{5!}}\left( { - {h^5}\frac{{{\partial ^5}u}}{{\partial {x^5}}} + 5{h^4}\tau a\frac{{{\partial ^6}u}}{{\partial {x^6}}} - } \right.\\ \left. {10{h^3}{\tau ^2}{a^2}\frac{{{\partial ^7}u}}{{\partial {x^7}}}} \right) + \frac{1}{{6!}}{h^6}\frac{{{\partial ^6}u}}{{\partial {x^6}}} + O\left( {{\tau ^4} + {h^7}} \right), \end{array} $ | (7) |
| $ u_j^{n + 1} = u_j^n + \tau \frac{{\partial u}}{{\partial t}} + \frac{{{\tau ^2}{a^2}}}{{2!}}\frac{{{\partial ^4}u}}{{\partial {x^4}}} + \frac{{{\tau ^3}{a^3}}}{{3!}}\frac{{{\partial ^6}u}}{{\partial {x^6}}} + O\left( {{\tau ^4}} \right), $ | (8) |
| $ \begin{array}{l} u_{j + 1}^{n + 1} = u_j^n + \left( {h\frac{{\partial u}}{{\partial x}} + \tau \frac{{\partial u}}{{\partial t}}} \right) + \frac{1}{{2!}}\left( {{h^2}\frac{{{\partial ^2}u}}{{\partial {x^2}}} + 2h\tau a\frac{{{\partial ^3}u}}{{\partial {x^3}}} + } \right.\\ \left. {{\tau ^2}{a^2}\frac{{{\partial ^4}u}}{{\partial {x^4}}}} \right) + \frac{1}{{3!}}\left( {{h^3}\frac{{{\partial ^3}u}}{{\partial {x^3}}} + 3{h^2}\tau a\frac{{{\partial ^4}u}}{{\partial {x^4}}} + 3h{\tau ^2}{a^2}\frac{{{\partial ^5}u}}{{\partial {x^5}}} + } \right.\\ \left. {{\tau ^3}{a^3}\frac{{{\partial ^6}u}}{{\partial {x^6}}}} \right) + \frac{1}{{4!}}\left( {{h^4}\frac{{{\partial ^4}u}}{{\partial {x^4}}} + 4{h^3}\tau a\frac{{{\partial ^5}u}}{{\partial {x^5}}} + 6{h^2}{\tau ^2}{a^2}\frac{{{\partial ^6}u}}{{\partial {x^6}}} + } \right.\\ \left. {4h{\tau ^3}{a^3}\frac{{{\partial ^7}u}}{{\partial {x^7}}}} \right) + \frac{1}{{5!}}\left( {{h^5}\frac{{{\partial ^5}u}}{{\partial {x^5}}} + 5{h^4}\tau a\frac{{{\partial ^6}u}}{{\partial {x^6}}} + 10{h^3}{\tau ^2}{a^2}\frac{{{\partial ^7}u}}{{\partial {x^7}}}} \right) + \\ \frac{1}{{6!}}{h^6}\frac{{{\partial ^6}u}}{{\partial {x^6}}} + O\left( {{\tau ^4} + {h^7}} \right), \end{array} $ | (9) |
| $ {\mathit{\Delta} _t}\left[ u \right]_{j - 1}^n = \frac{{u_{j - 1}^{n + 1} - u_{j - 1}^n}}{\tau }, $ | (10) |
| $ {\mathit{\Delta} _t}\left[ u \right]_j^n = \frac{{u_j^{n + 1} - u_j^n}}{\tau }, $ | (11) |
| $ {\mathit{\Delta} _t}\left[ u \right]_{j + 1}^n = \frac{{u_j^{n + 1} - u_j^n}}{\tau }, $ | (12) |
| $ \delta _x^2\left[ u \right]_{j - 1}^n = \frac{{u_{j - 2}^n - 2u_{j - 1}^n + u_j^n}}{{{h^2}}}, $ | (13) |
| $ \delta _x^2\left[ u \right]_j^n = \frac{{u_{j - 1}^n - 2u_j^n + u_{j + 1}^n}}{{{h^2}}}, $ | (14) |
| $ \delta _x^2\left[ u \right]_{j + 1}^n = \frac{{u_j^n - 2u_{j + 1}^n + u_{j + 2}^n}}{{{h^2}}}, $ | (15) |
| $ \delta _x^2\left[ u \right]_{j + 2}^n = \frac{{u_{j + 1}^n - 2u_{j + 2}^n + u_{j + 3}^n}}{{{h^2}}}. $ | (16) |
如果u是式(2)的光滑解, 即u满足
| $ \frac{{\partial u}}{{\partial t}} = a\frac{{{\partial ^2}u}}{{\partial {x^2}}} $ |
的光滑函数.结合式(2)进行整理, 便可导出下列差商的渐进表达式(其中aτ=h2r):
| $ \begin{array}{l} {\mathit{\Delta} _t}\left[ u \right]_{j - 1}^n = \frac{{u_{j - 1}^{n + 1} - u_{j - 1}^n}}{\tau } = \frac{{\partial u}}{{\partial t}} - ha\frac{{{\partial ^3}u}}{{\partial {x^3}}} + \\ \frac{{{h^2}a\left( {r + 1} \right)}}{2}\frac{{{\partial ^4}u}}{{\partial {x^4}}} - \frac{{{h^3}a\left( {3r + 1} \right)}}{6}\frac{{{\partial ^5}u}}{{\partial {x^5}}} + \frac{{{h^4}a}}{{24}}\left( {4{r^2} + 6r + } \right.\\ \left. 1 \right)\frac{{{\partial ^6}u}}{{\partial {x^6}}} + O\left( {{h^5}} \right), \end{array} $ |
| $ {\mathit{\Delta} _t}\left[ u \right]_j^n = \frac{{u_j^{n + 1} - u_j^n}}{\tau } = \frac{{\partial u}}{{\partial t}} + \frac{{{h^2}ar}}{2}\frac{{{\partial ^4}u}}{{\partial {x^4}}} + \frac{{{h^4}a{r^2}}}{6}\frac{{{\partial ^6}u}}{{\partial {x^6}}} + O\left( {{\tau ^3}} \right), $ |
| $ \begin{array}{l} {\mathit{\Delta} _t}\left[ u \right]_{j + 1}^n = \frac{{u_{j + 1}^{n + 1} - u_{j + 1}^n}}{\tau } = \frac{{\partial u}}{{\partial t}} + ha\frac{{{\partial ^3}u}}{{\partial {x^3}}} + \\ \frac{{{h^2}a\left( {r + 1} \right)}}{2}\frac{{{\partial ^4}u}}{{\partial {x^4}}} + \frac{{{h^3}a\left( {3r + 1} \right)}}{6}\frac{{{\partial ^5}u}}{{\partial {x^5}}} + \frac{{{h^4}a}}{{24}}\left( {4{r^2} + 6r + } \right.\\ \left. 1 \right)\frac{{{\partial ^6}u}}{{\partial {x^6}}} + O\left( {{h^5}} \right), \end{array} $ |
| $ \begin{array}{l} \delta _x^2\left[ u \right]_{j - 1}^n = \frac{{u_{j - 2}^n - 2u_{j - 1}^n + u_j^n}}{{{h^2}}} = \frac{{{\partial ^2}u}}{{\partial {x^2}}} - h\frac{{{\partial ^3}u}}{{\partial {x^3}}} + \\ \frac{7}{{12}}{h^2}\frac{{{\partial ^4}u}}{{\partial {x^4}}} - \frac{1}{4}{h^3}\frac{{{\partial ^5}u}}{{\partial {x^5}}} + \frac{{31}}{{360}}{h^4}\frac{{{\partial ^6}u}}{{\partial {x^6}}} + O\left( {{h^5}} \right), \end{array} $ |
| $ \begin{array}{l} \delta _x^2\left[ u \right]_j^n = \frac{{u_{j - 1}^n - 2u_j^n + u_{j + 1}^n}}{{{h^2}}} = \frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{1}{{12}}{h^2}\frac{{{\partial ^4}u}}{{\partial {x^4}}} + \\ \frac{1}{{360}}{h^4}\frac{{{\partial ^6}u}}{{\partial {x^6}}} + O\left( {{h^5}} \right), \end{array} $ |
| $ \begin{array}{l} \delta _x^2\left[ u \right]_{j + 1}^n = \frac{{u_j^n - 2u_{j + 1}^n + u_{j + 2}^n}}{{{h^2}}} = \frac{{{\partial ^2}u}}{{\partial {x^2}}} + h\frac{{{\partial ^3}u}}{{\partial {x^3}}} + \\ \frac{7}{{12}}{h^2}\frac{{{\partial ^4}u}}{{\partial {x^4}}} + \frac{1}{4}{h^3}\frac{{{\partial ^5}u}}{{\partial {x^5}}} + \frac{{31}}{{360}}{h^4}\frac{{{\partial ^6}u}}{{\partial {x^6}}} + O\left( {{h^5}} \right). \end{array} $ |
用上述差商建立含多个参数的差分算子
| $ \begin{array}{l} {L_h}\left[ u \right]_j^n = {c_1}{\mathit{\Delta} _t}\left[ u \right]_{j - 1}^n + {c_2}{\mathit{\Delta} _t}\left[ u \right]_j^n + {c_3}{\mathit{\Delta} _t}\left[ u \right]_{j + 1}^n - \\ a{c_4}\delta _x^2\left[ u \right]_{j - 1}^n - a{c_5}\delta _x^2\left[ u \right]_j^n - a{c_6}\delta _x^2\left[ u \right]_{j + 1}^n = 0 \end{array} $ | (17) |
来逼近微分算子
| $ \begin{array}{l} \left( {{c_1} + {c_2} + {c_3}} \right)\frac{{\partial u}}{{\partial t}} + \left( { - a{c_4} - a{c_5} - a{c_6}} \right)\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \\ \left( { - ha{c_1} + ha{c_3} + ha{c_4} - ha{c_6}} \right)\frac{{{\partial ^3}u}}{{\partial {x^3}}} + \left[ {\frac{{{h^2}a\left( {c + 1} \right)}}{2}{c_1} + } \right.\\ \left. {\frac{{{h^2}ar}}{2}{c_2} + \frac{{{h^2}a\left( {r + 1} \right)}}{2}{c_3} - \frac{{7{h^2}a}}{{12}}{c_4} - \frac{{{h^2}a}}{{12}}{c_5} - \frac{{7{h^2}a}}{{12}}{c_6}} \right]\frac{{{\partial ^4}u}}{{\partial {x^4}}} + \\ \left[ { - \frac{{{h^3}a\left( {3r + 1} \right)}}{6}{c_1} + \frac{{{h^3}a\left( {r + 1} \right)}}{6}{c_3} + \frac{{{h^3}a}}{4}{c_4} - \frac{{{h^3}a}}{4}{c_6}} \right] \times \\ \frac{{{\partial ^5}u}}{{\partial {x^5}}} + \left[ {\frac{{{h^4}a}}{{24}}\left( {4{r^2} + 6r + 1} \right){c_1} + \frac{{{h^3}a{r^2}}}{6}{c_2} + \frac{{{h^4}a}}{{24}}\left( {4{r^2} + 6r + } \right.} \right.\\ \left. {\left. 1 \right){c_3} - \frac{{31{h^4}a}}{{360}}{c_4} - \frac{{{h^4}a}}{{360}}{c_5} - \frac{{31{h^4}a}}{{360}}{c_6}} \right]\frac{{{\partial ^6}u}}{{\partial {x^6}}} = 0. \end{array} $ | (18) |
为了使式(18)的截断误差达到O(τ3+h5), 只需解下面方程组
| $ \left\{ \begin{array}{l} {c_1} + {c_2} + {c_3} - {c_4} - {c_5} - {c_6} = 0,\\ {c_1} - {c_3} - {c_4} + {c_6} = 0,\\ 6\left( {r + 1} \right){c_1} + 6r{c_2} + 6\left( {r + 1} \right){c_3} - 7{c_4} - {c_5} - 7{c_6} = 0,\\ - 2\left( {3r + 1} \right){c_1} + 2\left( {3r + 1} \right){c_3} + 3{c_4} - 3{c_6} = 0,\\ 15\left( {4{r^2} + 6r + 1} \right){c_1} + 60{r^2}{c_2} + 15\left( {4{r^2} + 6r + 1} \right){c_3} - \\ \;\;\;31{c_4} - {c_5} - 31{c_6} = 0. \end{array} \right. $ | (19) |
解得
| $ \left\{ \begin{array}{l} {c_1} = \frac{{ - 300{r^2} + 180r + }}{{3\left( {60{r^2} - 3} \right)}}{c_6},\\ {c_2} = \frac{{600{r^2} + 540r - 160}}{{3\left( {420{r^2} + 56r - 21} \right)}}{c_6},\\ {c_3} = \frac{{ - 300{r^2} + 180r - 25}}{{3\left( {60{r^2} - 3} \right)}}{c_6},\\ {c_4} = {c_6},\\ {c_5} = \frac{{ - 120{r^2} + 300r - 64}}{{60{r^2} - 3}}{c_6}. \end{array} \right. $ | (20) |
取c6=180r2-9, 有
| $ \left\{ \begin{array}{l} {c_1} = - 300{r^2} + 180r - 25,\\ {c_2} = 600{r^2} + 540r - 160,\\ {c_3} = - 300{r^2} + 180r - 25,\\ {c_4} = 180{r^2} - 9,\\ {c_5} = - 360{r^2} + 900r - 192. \end{array} \right. $ | (21) |
将式(21)代入到式(17)中, 得差分格式为
| $ \begin{array}{l} \left( { - 300{r^2} + 180r - 25} \right)u_{j - 1}^{n + 1} + \left( {600{r^2} + 540r - } \right.\\ \left. {160} \right)u_j^{n + 1} + \left( { - 300{r^2} + 180r - 25} \right)u_{j + 1}^{n + 1} = \left( {180{r^3} - 9r} \right)u_{j - 2}^n + \\ \left( { - 720{r^3} + 600{r^2} + 6r - 25} \right)u_{j - 1}^n + \left( {1080{r^3} - 1200{r^2} + } \right.\\ \left. {906r - 160} \right)u_j^n + \left( { - 720{r^3} + 600{r^2} + 6r - 25} \right)u_{j + 1}^n + \\ \left( {180{r^3} - 9r} \right)u_{j + 2}^n. \end{array} $ | (22) |
根据对称性可得其对称格式为
| $ \begin{array}{l} \left( { - 300{r^2} + 180r - 25} \right)u_{j + 1}^{n + 1} + \left( {600{r^2} + 540r - } \right.\\ \left. {160} \right)u_j^{n + 1} + \left( { - 300{r^2} + 180r - 25} \right)u_{j - 1}^{n + 1} = \left( {180{r^3} - } \right.\\ \left. {9r} \right)u_{j + 2}^n + \left( { - 720{r^3} + 600{r^2} + 6r - 25} \right)u_{j + 1}^n + \left( {1080{r^3} - } \right.\\ \left. {1200{r^2} + 906r - 160} \right)u_j^n + \left( { - 720{r^3} + 600{r^2} + 6r - } \right.\\ \left. {25} \right)u_{j - 1}^n + \left( {180{r^3} - 9r} \right)u_{j - 2}^n. \end{array} $ | (23) |
为了简化运算, 令
| $ A = - 300{r^2} + 180r - 25, $ |
| $ B = 600{r^2} + 540r - 160, $ |
| $ C = - 300{r^2} + 180r - 25, $ |
| $ D = 180{r^3} - 9r, $ |
| $ E = - 720{r^3} + 600{r^2} + 6r - 25, $ |
| $ F = 1080{r^3} - 1200{r^2} + 906r - 160, $ |
| $ G = - 720{r^3} + 600{r^2} + 6r - 25, $ |
| $ H = 180{r^3} - 9r. $ |
利用Fourier方法[7-10], 令ujn=vneijθ, 则式(22)可化为
| $ \begin{array}{l} A{v^{n + 1}}{{\rm{e}}^{i\left( {j - 1} \right)\theta }} + B{v^n}{{\rm{e}}^{ij\theta }} + C{v^{n + 1}}{{\rm{e}}^{i\left( {j + 1} \right)\theta }} = D{v^n}{{\rm{e}}^{i\left( {j + 2} \right)\theta }} + \\ E{v^n}{{\rm{e}}^{i\left( {j - 1} \right)\theta }} + F{v^n}{{\rm{e}}^{ij\theta }} + G{v^n}{{\rm{e}}^{i\left( {j + 1} \right)\theta }} + H{v^n}{{\rm{e}}^{i\left( {j + 2} \right)\theta }}, \end{array} $ | (24) |
即
| $ \begin{array}{l} A{v^{n + 1}}{{\rm{e}}^{ - i\theta }} + B{v^n}{{\rm{e}}^{i\theta }} + C{v^{n + 1}}{{\rm{e}}^{i\theta }} = D{v^n}{{\rm{e}}^{ - 2i\theta }} + E{v^n}{{\rm{e}}^{ - i\theta }} + \\ F{v^n} + G{v^n}{{\rm{e}}^{i\theta }} + H{v^n}{{\rm{e}}^{2i\theta }}. \end{array} $ | (25) |
令增长因子
| $ p = \left( {A + C} \right)\left( {1 - s} \right) + B + \left( {C - A} \right)i\sin \theta , $ | (26) |
| $ \begin{array}{l} q = \left( {2D + 2H} \right){s^2} + \left( { - 4D - E - G - 4H} \right)s + \\ \left( {D + E + F + G + H} \right) + \left[ { - 2D - E + G + 2H + \left( {2D - } \right.} \right.\\ \left. {\left. {2H} \right)s} \right]i\sin \theta . \end{array} $ | (27) |
将A, B, C, D, E, F, G, H的值代入式(26)和(27), 得
| $ \begin{array}{l} p = \left( { - 600{r^2} + 360r - 50} \right) + \left( {600{r^2} - 360r + 50} \right)s + \\ 600{r^2} + 540r - 160, \end{array} $ | (28) |
| $ \begin{array}{l} q = \left( {720{r^3} - 36r} \right){s^2} + \left( {720{r^3} - 1200{r^2} + 24r + } \right.\\ \left. {50} \right)s + 900r - 210, \end{array} $ | (29) |
| $ \begin{array}{l} {\left| {\frac{q}{4}} \right|^2} - {\left| {\frac{p}{4}} \right|^2} = \left( {32400{r^6} - 3240{r^4} + 81{r^2}} \right){s^4} + \\ \left( {64800{r^6} - 108000{r^5} - 1080{r^4} + 10080{r^3} - 108{r^2} - } \right.\\ \left. {234r} \right){s^3} + \left( {32400{r^6} - 10800{r^5} + 150660{r^4} + 9000{r^3} - } \right.\\ \left. {23814{r^2} + 3450r} \right){s^2} + \left( {81000{r^4} - 221580{r^3} + 59850{r^2} - } \right.\\ \left. {10176} \right)s, \end{array} $ | (30) |
要使格式(22)稳定的充要条件[6]是|q|2- |p|2≤0, 即
令
| $ \begin{array}{l} F\left( s \right) = \left( {32400{r^6} - 3240{r^4} + 81{r^2}} \right){s^4} + \left( {64800{r^6} - } \right.\\ \left. {108000{r^5} - 1080{r^4} + 10080{r^3} - 108{r^2} - 234r} \right){s^3} + \\ \left( {32400{r^6} - 10800{r^5} + 150660{r^4} + 9000{r^3} - 23814{r^2} + } \right.\\ \left. {3450r} \right){s^2} + \left( {81000{r^4} - 221580{r^3} + 59850{r^2} - } \right.\\ \left. {10176} \right)s, \end{array} $ | (31) |
则
| $ \begin{array}{l} F'\left( s \right) = 4\left( {32400{r^6} - 3240{r^4} + 81{r^2}} \right){s^3} + \\ 3\left( {64800{r^6} - 108000{r^5} - 1080{r^4} + 10080{r^3} - 108{r^2} - } \right.\\ \left. {234r} \right){s^2} + 2\left( {32400{r^6} - 10800{r^5} + 150660{r^4} + 9000{r^3} - } \right.\\ \left. {23814{r^2} + 3450r} \right)s + \left( {81000{r^4} - 221580{r^3} + 59850{r^2} - } \right.\\ \left. {10176} \right)r, \end{array} $ | (32) |
| $ \begin{array}{l} F''\left( s \right) = 12\left( {32400{r^6} - 3240{r^4} + 81{r^2}} \right){s^2} + \\ 6\left( {64800{r^6} - 108000{r^5} - 1080{r^4} + 10080{r^3} - 108{r^2} - } \right.\\ \left. {234r} \right)s + 2\left( {32400{r^6} - 10800{r^5} + 150660{r^4} + 9000{r^3} - } \right.\\ \left. {23814{r^2} + 3450r} \right), \end{array} $ | (33) |
| $ \begin{array}{l} F'''\left( s \right) = 24\left( {32400{r^6} - 3240{r^4} + 81{r^2}} \right)s + \\ 6\left( {64800{r^6} - 108000{r^5} - 1080{r^4} + 10080{r^3} - 108{r^2} - } \right.\\ \left. {234r} \right), \end{array} $ | (34) |
从而, 式(22)稳定的充要条件是F(s)≤0.
下证式(22)稳定的一个充分条件.受文献[7-8]的启发, 能得出以下两个引理.
引理1 0.001 < r < 0.231或0.236 < r < 0.772是F(s)≤0, s∈[0, 2]成立的一个充分条件.
证明 由函数的单调性及凸性,
| $ \begin{array}{l} F\left( s \right) \le 0 \Leftarrow \left\{ \begin{array}{l} F''\left( s \right) \ge 0\\ F\left( 0 \right) \le 0\\ F\left( 2 \right) \le 0 \end{array} \right. \Leftarrow \left\{ \begin{array}{l} F''\left( 0 \right) \ge 0\\ F''\left( 2 \right) \ge 0\\ F\left( 0 \right) \le 0\\ F\left( 2 \right) \le 0 \end{array} \right.\\ \Leftrightarrow r \in \left( {0.001,0.231} \right) \cup \left( {0.236,0.772} \right). \end{array} $ |
故r∈(0.001, 0.231)∪(0.236, 0.772)是F(s)≤0, s∈[0, 2]成立的一个充分条件.
引理2 0.001 < r < 0.023是F(s)≤0, s∈[0, 2]成立的一个充分条件.
证明 由函数的单调性及凸性,
| $ \begin{array}{l} F\left( s \right) \le 0 \Leftarrow \left\{ \begin{array}{l} F'\left( 0 \right) \ge 0\\ F\left( 2 \right) \le 0 \end{array} \right. \Leftarrow \left\{ \begin{array}{l} F'\left( 0 \right) \ge 0\\ F'\left( 2 \right) \ge 0\\ F\left( 2 \right) \le 0\\ F''\left( 0 \right) \le 0\\ F''\left( 2 \right) \le 0 \end{array} \right.\\ \Leftrightarrow r \in \left( {0.001,0.023} \right). \end{array} $ |
故r∈(0.001, 0.023)是F(s)≤0, s∈[0, 2]成立的一个充分条件.
由此, 根据引理1, 引理2得出下面定理.
定理1 格式(23)的截断误差是O(τ3+h5), 且在0.001 < r < 0.231或0.236 < r < 0.772时, 格式稳定.
3 数值算例对初边值问题:
| $ \left\{ \begin{array}{l} \frac{{\partial u}}{{\partial t}} = \frac{{{\partial ^2}u}}{{\partial {x^2}}},0 \le x \le {\rm{ \mathsf{ π} }} ,t \ge 0,a > 0,\\ u\left( {x,0} \right) = \sin x,0 \le x \le {\rm{ \mathsf{ π} }} ,\\ u\left( {0,t} \right) = u\left( {{\rm{ \mathsf{ π} }},t} \right) = 0,t \ge 0, \end{array} \right. $ | (35) |
已知该问题的精确解为u(x, t)=e-tsinx, 利用式(22)、(23)以及精确解进行数值模拟[15].模拟结果如图 2所示.为方便起见, 初边值问题(40)的精确解u(x, t)=e-tsinx给出第一层的值uj1.
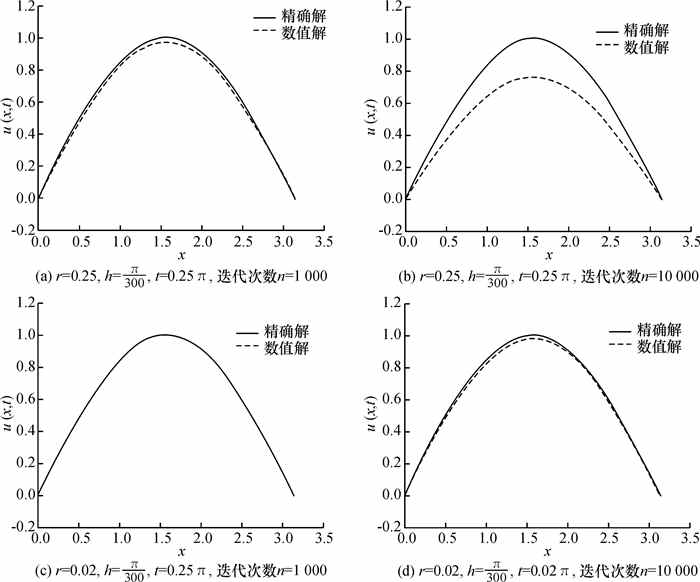
|
图 2 模拟结果 Figure 2 Fitting results |
由图 2可知, 对于不同的r, 差分式(22)的数值解与精确解都有较好的吻合, 这个数值结果与理论分析是完全一致的, 说明算法的可行性和有效性.
| [1] |
金承日. 解抛物型方程的高精度显式差分格式[J].
计算数学, 1991, 13(1): 38-44.
Jin C R. The High accuracy explicit difference scheme for solving parabolic equations[J]. Mathematica Numerica Sinica, 1991, 13(1): 38-44. |
| [2] |
马明书. 解抛物型方程的一个高精度两层显格式[J].
河南师范大学学报, 1996, 24(1): 80-81.
Ma M S. A high accuracy two level explicit difference scheme for solving parabolic equations[J]. Journal of Henan Normal University:Natural Science Edition, 1996, 24(1): 80-81. |
| [3] |
葛永斌, 吴文权, 卢曦. 解二维扩散方程的高精度多重网格方法[J].
工程热物理学报, 2002, 23(S): 121-124.
Ge Y B, Wu W Q, Lu X. High accuracy multigrid solution of 2-D diffusion equation[J]. Journal of Engineering Themrmophysics, 2002, 23(S): 121-124. |
| [4] |
葛永斌, 田振夫, 吴文权. 三维抛物型方程的两种加权平均隐式多重网格方法[J].
工程数学学报, 2003, 20(3): 105-110.
Ge Y B, Tian Z F, Wu W Q. Multigrid solutions based on two classes of weighted average implicit schemes of three-dimensional parabolic equation[J]. Journal of Engineering Mathematics, 2003, 20(3): 105-110. |
| [5] |
葛永斌, 田振夫, 吴文权. 二维抛物型方程的高精度多重网格解法[J].
应用数学, 2003, 16(2): 13-18.
Ge Y B, Tian Z F, Wu W Q. A high accuracy mutltigrid method for 2-D parabolic equation[J]. Mathematicia Applicata, 2003, 16(2): 13-18. |
| [6] |
张莉, 张大凯. 解抛物型方程组合差商法[J].
贵州大学学报, 2004, 21(4): 349-353.
Zhang L, Zhang D K. Combinatorial difference quotient method for solving parabolic equations[J]. Journal of Guizhou University: Natural Science Edition, 2004, 21(4): 349-353. |
| [7] |
张莉, 袁伟, 张大凯. 求解抛物型方程具较高精度的半显差分格式[J].
山东农业大学学报, 2008, 39(4): 637-640.
Zhang L, Yuan W, Zhang D K. The higher-precise semi-explicit difference scheme for solving parabolic equations[J]. Journal of Shandong Agricultural University, 2008, 39(4): 637-640. |
| [8] |
陈泽龙, 张大凯. 解抛物型方程的七点半显差分格式[J].
贵州大学学报, 2006, 23(1): 31-34.
Chen Z L, Zhang D K. The semi-explicit differencing scheme of seven points for sloving the parabolic equations[J]. Journal of Guizhou University:Natural Science Edition, 2006, 23(1): 31-34. |
| [9] |
徐金平, 单双荣. 解抛物型方程的一个高精度显式差分格式[J].
华侨大学学报, 2009, 30(4): 473-475.
Xu J P, Shan S R. An Explicit difference scheme with high-order accuracy for solving parabolic equation[J]. Journal of Huaqiao University, 2009, 30(4): 473-475. DOI: 10.11830/ISSN.1000-5013.2009.04.0473. |
| [10] |
王爱锋, 曲小钢. 解抛物型方程的一种隐式差分格式[J].
纺织高校基础科学学报, 2010, 23(4): 393-395.
Wang A F, Qu X G. An implicit differencing scheme for solving the parabolic equation[J]. Basic Sciences Journal of Textile Universities, 2010, 23(4): 393-395. |
| [11] |
Zhang J. Fast and high accuracy multigrid solution of the three dimensional poisson equation[J].
J Comp Phys, 1998, 143(2): 449-461.
DOI: 10.1006/jcph.1998.5982. |
| [12] |
余德浩, 汤华中.
微分方程数值解法[M]. 北京: 科学出版社, 2003.
|
| [13] |
Morton K W, Mayers D F. 偏微分方程数值解[M]. 李治平, 门大力, 许现明, 等译. 北京: 人民邮电出版社, 2005.
|
| [14] |
戴嘉尊, 邱建贤.
微分方程数值解法[M]. 南京: 东南大学出版社, 2012.
|
| [15] |
王沫然.
Matlab与科学计算[M]. 北京: 科学出版社, 2003.
|
 2014, Vol. 31
2014, Vol. 31