20世纪80年代以来,随着产品更新换代速度的加快,被消费者淘汰和丢弃的商品不断增多;同时,社会对环保日益关注,可利用资源的日益匮乏,引起了人们对于逆向物流的重视.伴随着逆向物流的兴起,社会中逐渐出现了一些第三方物流回收企业,它们负责对上游产品进行运输、存储、配送,对下游旧产品进行回收、拆分、加工和运输,由此获得利润,而且承担相应的成本.加强对正逆向物流费用的管理对于降低成本、提高企业经济效益具有明显的意义[1-2].与单向物流不同[3-4],逆向物流成本需考虑双向运输、新旧产品库存与回收等因素,在不同费用下,企业对于物流活动的安排与单向物流会有所不同.对于中小企业来说,没有能力同时处理上下游的产品,在这种情况下,就需要找到一种工作任务合理的循环模式和循环次数(即运输计划),使两类产品被有序地加工并且配送.本文的研究旨在降低企业因正逆向物流不合理的循环而产生的成本,并且使企业根据最优的循环来确定适当的库存,最终优化总成本.
1 研究背景“逆向物流”的概念最早是由Stock在1992年提出的,他指出逆向物流为一种包含了产品退回、物料替代、物品再利用、废弃处理、再处理、维修与再制造等流程的物流活动[5].国内学者对于逆向库存模式的研究较欠缺,而国外的一些学者对于逆向物流和再制造的研究主要集中在回收网络优化与选择、库存控制策略等方面[6-10].Richter研究了生产与循环需求不变的情况,假设新产品的生产与回收品的再制造都是瞬时进行的,并且市场上的需求由新产品和再制造产品两部分组成,每个周期包括单一的生产与再制造循环[11];Dobos在Richter的基础上,研究了非瞬时生产与再制造的情况;之后,Dobos又把先前的模型推广成多产品的生产与回收再制造的情况[12];Jaber考虑了新产品与再制造产品存在质量差异的情况,并且二者不可以相互替换[13].Guide定量地分析了回收价格与产品数量的关系[14];而后,Guide又研究了利用旧产品的价格控制旧产品回收率和销售率,并且从供应链角度建立了一个模型,但没有考虑库存成本,也没有给出回收率与回收价格的定量关系[15];Karakayali在供应链的角度讨论了回收定价机制的问题,并且给出回收数量与回收价格的定量关系,也同样没有考虑库存成本.
本文在前人研究[16-17]的基础上进行创新,通过假设市场对于新旧产品需求的不同,拓展了Jaber的模型,加入了物流循环启动成本、产品收集成本等一系列变量,并且利用EOQ模型研究最优库存,然后利用最优库存控制正逆向物流的运输计划,得出最佳运输策略,用搜索算法寻找最优解,最后用Matlab计算得出结果.
2 数学建模 2.1 模型假设本文假设同一种产品有不同的质量,装卸、搬运、流水作业的速度是有限的,正逆向物流不能同时进行,消费者认为新旧产品质量不同,单位时间内对新产品和旧产品的处理速率不同,初级市场与二手市场的旧产品回收率是不同的,没有库存缺货和需求的不满足的发生,不限制库存能力.另外,本文假设初级市场只销售新产品,二手市场只销售再制造产品.相关变量如下:
n:T时间间隔内正向物流运输的次数
m:T时间间隔内逆向物流运输的次数
γp:初级市场上旧产品回收的百分比
γr:二手市场上旧产品回收的百分比
Dp:新产品流通过程处理的速度
Dr:旧产品流通过程处理的速度
Sp:单次正向物流的运输成本
Sr:单次逆向物流的运输成本
Wp:单位新产品的采购成本
Wr:单位旧产品的收集成本
Rp:正向物流启动成本
Rr:逆向物流启动成本
Lp:单位时间正向物流的人工处理成本
Lr:单位时间逆向物流的人工处理成本
hp:新产品在单位时间的持有成本(企业1)
hr:旧产品在单位时间的持有成本(企业2)
hu:旧产品在单位时间的持有成本(企业2)
cp:每单位新产品的销售损失的惩罚成本
cr:每单位旧产品的销售损失的惩罚成本
βp:初级市场旧产品回收可利用的百分比
βr:二手市场旧产品回收可利用的百分比
(0 < βr≤βp < 1)记1-βr和1-βp为旧产品报废概率
x1:T时间间隔内新产品被运来的数量
x2:T时间间隔内旧产品被运回的数量
Tp:前向物流时间间隔的长度Tp=x1/Dp
Tr:逆向物流时间间隔的长度Tr=x2/Dr
T:总时间间隔的长度T=Tp+Tr
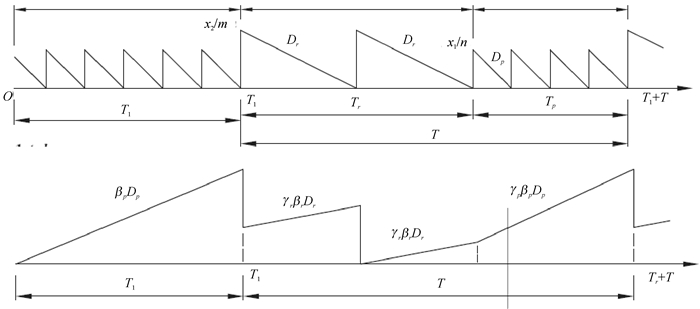
2.2 数学模型本文是基于Richter描述的再制造模型建立的,模型情景里有两个企业.第一家企业负责运输新产品和旧产品,第二家企业只负责收集旧产品.在每个T时间间隔内,有m次逆向物流循环和n次正向物流循环.物流循环系统如图 1所示.

|
图 1 物流运输系统 Figure 1 The transportation system of logistics |
在一个T的时间间隔内,有两个短间隔Tr、Tp分别代表逆向物流和正向物流的活动时间.一个逆向物流时间间隔内有m个数量大小为x2/m的批次,一个正向物流的时间间隔内有n个数量大小为x1/n的批次.T的时间间隔内总的正逆向物流处理后运输的数量分别是x1=DpTp和x2=DrTr.在Tr时间间隔内二手市场再制造产品的回收并且可利用率是γrβr,Tp时间间隔内初级市场旧产品的回收并且可以用率是γpβp,累计可得x2=γrβrDrTr+γpβpDpTp,相应的可以得到
| $ {x_1}/{x_2} = \left( {1-{\gamma _r}{\beta _r}} \right)/{\gamma _p}{\beta _p}, $ | (1) |
表示的是新产品与旧产品运输数量的比率.对于第一个时间间隔[0, T1]内,企业1只进行正向物流而不进行逆向物流,企业2只进行旧产品的回收.从第二个时间间隔开始,m个批次的逆向物流活动优先于n个批次的正向物流活动.在T时间间隔内的正向物流、逆向物流、旧产品收集的库存活动见图 2.本文考虑了一种情况就是假设在进行正向物流活动的期间,供应链上游企业就会得不到对旧产品的需求,反之亦然.T的时间间隔内全部成本包括:正逆向物流的运输成本,新旧产品的持有成本,新旧产品的缺货成本.模型为式(2)、(3).
|
图 2 运输企业与回收企业的库存情况 Figure 2 The inventory conditions of transportation and recycling enterprises |
| $ \begin{array}{*{20}{l}} {\Psi \left( {n,m,{x_2},{\gamma _p},{\gamma _r}} \right) = {R_r} + {R_p} + m{S_r} + n{S_p} + }\\ {\frac{{{h_r}}}{{2m{D_r}}}{x_2}^2 + \frac{{{h_p}}}{{2n{D_p}}}{x_1}^2 + {h_u}\left[ {\left( {\frac{{m({\gamma _r}{\beta _r} - 1) + 1}}{{2m{D_r}}}} \right)} \right.{x_2}^2 + }\\ {\left. {\frac{{{\gamma _p}{\beta _p}}}{{2{D_p}}}{x_1}^2 + \left( {\frac{{{\gamma _r}{\beta _r}}}{{m{D_p}}} + \frac{{{\gamma _p}{\beta _p}(m - 1)}}{{m{D_r}}}} \right){x_1}{x_2}} \right] + {W_r}{x_2} + }\\ {{W_p}{x_1} + {L_r}{T_r} + {L_p}{T_p} + {c_r}{D_r}{T_p} + {c_p}{D_p}{T_r},} \end{array} $ | (2) |
| $ \begin{array}{l} {x_1}/{x_2} = \left( {1- {\gamma _p}{\beta _r}} \right)/{\gamma _p}{\beta _p}, \\ {T_1} = \frac{{{x_2}}}{{{\beta _p}{D_p}}}\left[{1-\frac{{{\gamma _p}{\beta _r}(m-1{\rm{)}}}}{m}} \right]. \end{array} $ | (3) |
mSr+nSp+Rp+Rr在式(2)中代表在T时间间隔内总的物流活动运输成本和启动成本.在T时间间隔内有m个逆向物流过程,每个过程的时间是Tr/m,流通x2/m件货物;同样,有n个正向物流的过程,每个过程的时间是Tp/n,流通x1/n件货物.在逆向物流Tr的时间内,单位时间流通货物的速度是x2/2m,正向物流Tp的时间内,单位时间流通货物的速度是x1/2n,因此旧产品的持有成本是hr× (x2/m) × (Tr/Dr)×m=x22hr/(2mDr),同样,正向物流新产品的持有成本是hp× (x1/n) × (Tp/Dp) ×n=x12hp/(2nDp).因为本文假设在逆向物流期间,不能进行正向物流,新产品的需求得不到,同样,在正向物流期间,不能进行逆向物流,再制造商对于旧产品的需求就满足不了,所以T时间间隔内的总的缺货损失成本crDrTp+cpDpTr,采购成本与收集成本为Wrx2+Wpx1,T时间间隔内人工处理成本为LγTγ+LpTp,T=Tp+Tγ,Tγ=x2/Dγ,Tp=x1/Dp,x1/x2=(1-γpβr)/γpβp,简化公式如下:
| $ \begin{array}{l} A = \frac{{{x_2}}}{{{x_1}/{D_p} + {x_2}/{D_r}}} = \frac{1}{{\left( {\frac{{(1- {\gamma _p}{\beta _r})}}{{{\gamma _p}{\beta _p}{D_p}}} + \frac{1}{{{D_r}}}} \right)}}, \\ {B_{pr}}({\gamma _p}, {\gamma _p}) = \left( {{W_p} + \frac{{{L_p}}}{{{D_p}}} + \frac{{{c_r}{D_r}}}{{{D_p}}}} \right)\left( {\frac{{1- {\gamma _p}{\beta _r}}}{{{\gamma _p}{\beta _p}}}} \right) + \\ \left( {{W_r} + \frac{{{L_r}}}{{{D_r}}} + \frac{{{c_p}{D_p}}}{{{D_r}}}} \right), \\ C\left( {n, m, {\gamma _p}, {\gamma _p}} \right) = \\ {h_u}\left[\begin{array}{l} \left( {\frac{{m({\gamma _p}{\beta _r}-1) + 1}}{{2m{D_r}}}} \right) + \frac{{{\gamma _p}{\beta _p}}}{{2{D_p}}}{\left( {\frac{{1-{\gamma _p}{\beta _r}}}{{{\gamma _p}{\beta _p}}}} \right)^2}\\ + \left( {\frac{{{\gamma _p}{\beta _r}}}{{m{D_p}}} + \frac{{{\gamma _p}{\beta _p}(m-1)}}{{m{D_r}}}} \right)\left( {\frac{{1 - {\gamma _p}{\beta _r}}}{{{\gamma _p}{\beta _p}}}} \right) \end{array} \right] + \frac{{{h_r}}}{{2m{D_r}}} + \\ \frac{{{h_p}}}{{2n{D_p}}}{\left( {\frac{{1 - {\gamma _p}{\beta _r}}}{{{\gamma _p}{\beta _p}}}} \right)^2}, \\ \psi \left( {n, m, {x_2}, {\gamma _p}, {\gamma _p}} \right) = \frac{A}{{{x_2}}}[m{S_r} + n{S_p} + {R_r} + {R_p} + \\ {x_2}{B_{pr}}\left( {{\gamma _p}, {\gamma _p}} \right) + {x_2}^2C\left( {n, m, {\gamma _p}, {\gamma _p}} \right)]. \end{array} $ | (4) |
因为式(4)关于x2的二阶导数为2A[m(Sr+Rr)+n(Sp+Rp)]/x23>0, 因此让式(4)关于x2的一阶导数为零可以得到最优解:
第1步,需要对输入参数进行赋值,然后令n=1,m=1,对ψ (1, 1, γp, γp)进行计算,记录下ψ (1, 1, γp, γp)、γp*(1, 1)、γr* (1, 1)的值.第2步,令m=2,重复第一步的计算,记录ψ (1, 2, γp, γp)、γr* (1, 2)、γp* (1, 2).然后比较临近值,如果ψ (1, 1, γp, γp) < ψ (1, 2, γp, γp),则结束对n的探索,如果ψ (1, 1, γp, γp) >ψ (1, 2, γp, γp),对m=3、m=4进行重复的探索,直到找出最优值m1*,使得ψ (1, m1*-1, γp, γp)>ψ (1, m1*, γp, γp) < ψ (1, m1*+1, γp, γp)成立,此时结果表示的是一次正向物流循环次数下,最优的逆向物流循环次数,记录下ψ (1, m1*, γp, γp),m1*,γp*(1, m1*),γr*(1, m1*)的值.第3步,令n=2时重复前两步的过程.比较ψ(1, m1*, γp, γp)和ψ (2, m2*, γp, γr),以此类推.最后,通过以上的过程,本文得到一个最优解ψ(1, mi*, -1, γp, γr) ≥ψ(1, mi*, γp, γr < ψ(1, m1*, +1, γp, γp),i表示最优的正向物流循环次数,m1*表示最优的逆向物流循环次数,单位时间内的最低成本是ψ(1, mi*, γp, γp).
2.4 算例检验因为本文做出此模型的目的是通过对比不同运输循环的选择,来得出单位时间内的总成本最小,所以本文暂不考虑取值区间对于γp, γr的影响,给它们进行赋值验算,假设Dp=Dr=200, Sp=200, Sr=150, hp=6, hr=3, hu=3, cp=cr=2, Lr=12,Lp=10,Rr=800,Rp=600,βr=0.667,βp=0.667,γp=γr=1,Wr=Wp=1可以得出结果,见表 1.
| 表 1 算例解法过程 Table 1 The process of example solution |
计算结果表明,从单次循环向多次循环变化的过程中,单位时间总成本先减少后上升,在某个运输计划下达到成本最低值,显而易见,当m=4且n=1时,单位时间达到最低值2 043.121,说明在一个T时间段内,逆向物流循环4次,正向物流循环1次所产生的单位时间成本最少,当然,变量取值不同,计算结果也会随之不同.本文在前人文献的基础上还增加了对于收集成本和采购成本的讨论.收集成本和采购成本通过影响不同市场上旧产品回收率来影响总成本,因此,把成本控制在一定的范围内时,不同的收集成本与采购成本将会对应不同的运输计划.假设当ψ(n, m)在[1 850, 2 200]范围内取值时,计算结果见表 2.
| 表 2 Wr、Wp对于成本的灵敏度分析 Table 2 Wr、Wp to the sensitivity analysis of costs |
当保持其他参数值固定不变时,讨论Wr和Wp在离散变化的情况下,m、n、γr、γp的变动对成本的影响,前提是回收率是随着回收成本的增大而减小,随着采购成本的增大而增大的.由表 2可以得出,随着Wr的增大,同时m的减小,会造成ψ(n, m)的减小,并在γr=0,γp=1时达到最小值,说明回收成本对总成本的影响弱于循环次数.同样可以得出,由于Wp的增大,ψ(n, m)会随着增大,但是在Wp增大时控制n的值变小,成本则会减小,说明采购成本对总成本的影响同样弱于循环次数.以上得知,企业对于总成本的控制应该更多地关注物流循环的优化.
3 结论本文假设新产品与再制造产品对于消费者来讲是不同的,并且通过合理考虑运输成本、旧产品收集成本、新产品采购成本、正逆向物流启动成本来扩展了Jaber等学者的模型.考虑到各类成本的不同,也会影响到运输计划的选择,因此本文推导出成本计算公式去寻找合理的运输计划,并通过算例去检验成本计算公式的可行性,得到不同的运输计划下总成本的变化情况.另外,还对一些参数做了灵敏度分析,结果表明,在既定的成本范围内不同的参数值对应不同的最优运输计划,并得出结论:在既定的成本范围内,对于初级市场与二手市场的旧产品采取全部回收的策略并不是最优的,在超过一定的取值范围时需要采取相对极端的回收方式,才能使得成本最优.
本文假设产品处理速度是不变的,但是实际的处理速度是在一定的取值范围内随机变化的,并且实际的库存水平在不同的时间点上也是随机波动的;消费者对于产品的需求也是随机的;另外,本文并没有考虑订货与运输提前期对于库存的影响,没有引入安全库存的思想,在今后的研究中需考虑这些因素对模型和优化结果的影响.
| [1] |
甘卫华. 逆向物流[M]. 北京大学出版社, 2012.
|
| [2] |
Ostlin, Sundin. Importance of closed-loop supply chain relationships for product remanufacturing[J].
International Journal of Production Economics, 2008, 2(115): 336-388.
|
| [3] |
许欢, 温洁嫦. 差分进化算法在物流配送路径优化中的应用[J].
广东工业大学学报, 2013, 30(4): 61-65.
Xu H, Wen J C. Application of differential evolution algorithm in optimizing the logistics distribution vehicle routing problem[J]. Journal of Guangdong University of Technology, 2013, 30(4): 61-65. |
| [4] |
温金保, 蔡延光. 基于自适应小生境遗传算法的物流配送路径优化研究[J].
广东工业大学学报, 2011, 28(1): 20-23.
Wen J B, Cai Y G. On the optimization of logistics distribution route based on self-adaption niche genetic algorithm[J]. Journal of Guangdong University of Technology, 2011, 28(1): 20-23. |
| [5] |
徐家旺, 朱云龙. 闭环供应链管理的研究进展[J].
系统工程, 2008, 8(26): 1-6.
Xu J W, Zhu Y L. Research progress of closed-loop supply chain management[J]. Systems Engineering, 2008, 8(26): 1-6. |
| [6] |
Serge L. A reverse logistics decisions conceptual framework[J].
Computers & Industrial Engineering, 2011, 3(61): 561-581.
|
| [7] |
Barker T J, Zabinsky Z B. Reverse logistics network design:A conceptual framework for decision making[J].
International Journal of Sustainable Engineering, 2008, 1(4): 250-260.
DOI: 10.1080/19397030802591196. |
| [8] |
Kannan G. Analysis of third party reverse logistics provider using interpretive structural modeling[J].
Int J Production Economics, 2012, 1(140): 204-211.
|
| [9] |
Kannan G. Analyzing supplier development criteria for an automobile industry[J].
Industrial Management & Data Systems, 2010, 1(110): 43-62.
|
| [10] |
Lee D H, Dong M. Dynamic network designfor reverse logistics operations under uncertainty[J].
Transportation Research Part E, 2009, 1(45): 61-71.
|
| [11] |
Richter. The EOQ repair and waste disposal model with variable setup numbers[J].
European Journal of Operational Research, 1996, 95(2): 313-324.
DOI: 10.1016/0377-2217(95)00276-6. |
| [12] |
Dobos, Richter. An extended production/recycling model with stationary deamand and return rates[J].
International Journal of Production Economics, 2004, 90(3): 311-323.
DOI: 10.1016/j.ijpe.2003.09.007. |
| [13] |
Jaber M Y, EI Saadany A MA. The production remanufacture and waste disposal model with lost sales[J].
International Journal of Production Economics, 2009, 120(1): 115-224.
DOI: 10.1016/j.ijpe.2008.07.016. |
| [14] |
Guide D, Van Wassenhove L N. Management product returns for remanufacturing[J].
Product Operation andManagement, 2001, 10(2): 142-155.
|
| [15] |
Guide D, Harrion T P. Matching demand and supply to maximize profit from remanufacturing[J].
Manufacturing and Service Operation Management, 2003, 5(4): 303-316.
DOI: 10.1287/msom.5.4.303.24883. |
| [16] |
雷定猷, 汤波. 再生资源回收物流网络优化模型与算法研究[J].
计算机应用研究, 2012, 29(6): 2093-2097.
Lei D Y, Tang B. Research on optimal model and algorithm for recycling logistics network planning of renewable resources[J]. Application Research of Computers, 2012, 29(6): 2093-2097. |
| [17] |
贺超, 庄玉良. 基于物联网的逆向物流管理信息系统构建[J].
中国流通经济, 2012, 26(6): 30-34.
He C, Zhuang Y L. Study on reverse logistics management information system based on internet of things[J]. China Business and Market, 2012, 26(6): 30-34. |
 2014, Vol. 31
2014, Vol. 31