经济结构调整和产业升级要求制造业产品的竞争方式逐渐由规模制胜转变成以速度和创新取胜[1].在产品设计中,方案设计是形成产品主要结构和参数的初步设计阶段,决定了产品最终价值的70%~80%[2],是产品致胜关键.方案设计是在需求分析基础上进行“创新构思—功能求解—评价决策”的过程,具有信息不完全性和多解性的特点,它要求设计人员在具备丰富理论知识和设计经验的同时,更重要的是要具备很强的方案拓展能力[3].目前方案设计更多依靠人的创造性劳动,对于复杂产品来说加大了设计人员的难度.如果计算机具备这种拓展能力,便能发挥其速度快、存储量大的优势,以更快的速度提供更多可供选择的设计方案,从而更有可能得到最优的设计方案,促进产品在竞争中取胜.
计算机具有拓展能力的关键是将拓展思维形式化并赋之于软件系统之中.发散思维是思维拓展的核心,发散思维注重的是思维的辐射作用,是创造力的主要来源[4].关于思维的形式化,我国科学家钱学森认为:“人的思维是有规律的,计算机模拟是研究思维的有效工具”,并预言“网络图可以实现发散思维”[5].在思维的形式化方面,可拓学进行了有益的尝试.可拓学是研究事物拓展可能性及开拓创新规律的科学.它用计算机可以理解的形式语言表达问题并建立一套可操作的推理技术,并为策略生成提供可操作的方法[6].为实现拓展思维,可拓学以物元模型及其变换为基础,研究了基于物、特征、特征参数及特征元变换的多种拓展原理,使多角度寻找问题答案成为可能[7].已有多位学者将这些原理应用于产品的创新构思中:杨春燕等人应用物元拓展推理提出了新产品创新构思的方法[8],赵燕伟等人将多级菱形思维模型应用于刀具库的方案设计[9].这些研究都针对具体问题通过形式化的拓展模型对创新构思进行了有益的探索.
方案拓展若想在智能系统中实现,必须从人工智能/知识工程的角度系统研究拓展思维模型在软件化过程中遇到的知识表示和知识推理等问题.知识表示是推理的前提.在知识表示方面,刘晓平等人通过实例说明了物元知识表示方法在创新设计中优于传统框架和语义网络[10],但没有将体现创新思维的可拓推理规则体现在知识库中.本文在前期研究工作中针对设计的知识特点建立了基于可拓模型的知识表示,并给出了可拓知识表示的定义、语法规范及数据结构[11],形式化地描述“物”的多种变化可能性,从而增加了对拓展思维的支持.在推理方面,杜春彦[12]根据可拓学理论, 给出了可拓推理模型和可拓推理的有关概念,陈文伟[13]等人根据归结原理证明了获取变化知识的两条可拓推理规则,杨国为[14]等人提出了基于物元与或网的启发式搜索算法和可拓继承推理.上述学者在可拓推理的研究方面具有开创意义,但知识推理系统的关键是推理规则的组织实施,只有有效的组织协调推理规则才能体现思维及拓展的过程.为此,本文在前人及前期工作的基础上,从可拓学中提取体现拓展思维特点的可拓推理规则,通过构建可拓网络图来组织协调推理规则的运用,建立基于可拓网络图的拓展思维推理体系,并将其应用于水轮发电机产品的方案设计之中,以期利用计算机技术实现创新构思,通过对设计方案的智能拓展快速高效地拓展出更多可供选择的设计方案.
1 设计方案的形式化拓展原理 1.1 物的拓展原理为实现拓展思维,可拓学用物元的可拓展性形式化地描述了物的各种拓展形式,包括设计领域广泛应用的发散性、相关性和蕴含性等.发散性给出了从不同角度寻找问题可能答案的途径,是实现发散思维的根本动力,用符号R1┤R2来表示,其中R1为原始物元,R2为发散后的物元.相关性和蕴含性描述了物之间的内在联系,分别用符号R1 ~ R2和R1⇒R2来表示.关于发散推理和相关蕴含推理的具体描述请参见文献[15].
1.2 可拓网络图物元的可拓展性描述了事物的拓展原理,包括发散性、相关性和蕴含性等.发散性是创造力的主要动力,然而如同盲目发散会使人的头脑产生混沌一样,在计算机世界里,盲目发散也会带来效率低下和组合爆炸等问题,如何组织协调物元之间的发散是方案拓展的重要任务.本文定义了可拓网络图并用来组织协调各可拓展性的应用.
定义1 (物元的可拓关系) 设W为全体物元集即W=W(Γ)={Γ|Γ∈£(R)},称有序偶<R1, R2> (R1∈W, R2∈W)为物元R1到R2的可拓关系,若存在映射关系φ:R1×R2→ф, ф={发散性, 相关性, 蕴含性, ……}.
可拓关系<R1, R2>说明物元R1和R2之间存在可拓展性,包括发散性、相关性和蕴含性等.
定义2 (可拓网络图) 设W为全体物元集即W=W(Γ)={Γ|Γ∈£(R)},U⊆W为论域,则称G(Γ)=<V, H>, (V⊆U)为可拓网络图,若对于任意Γ, Γi∈V,都有<Γ, Γi>∈H且有向边<Γ, Γi>满足Γ~Γi或Γ⇒Γi(i=1, 2, …, n). V称为G(Γ)的顶点集,H称为G(Γ)的有向边集.
可拓网络图是物元结点及其可拓关系集合构成的顶点活动网(AOV, Activity On Vertex),是同论域可拓图的子图.可拓网络图将物元及其描述物元间内在联系的相关性和蕴含性构成一张关系网,是可能具有多重边和环结构的非简单图,其中不可避免会产生冲突.冲突的存在会降低知识库系统的推理效率,甚至会使推理过程中断造成求解失败.因此有必要对可拓网络图的冲突进行判定和消解.一般地,冲突主要有知识冲突和路径冲突两种形式.
定义3 对于可拓网络图G=<V, H>上的任意两个物元结点R1和R2,若存在边集I={<R1, R2>|R1×R2→ω, R1, R2∈V, ω∈{相关性, 蕴含性}}⊆H且|I|≥2时,则认为在可拓图G中的结点R1和R2之间存在知识冲突.
对于定义3的含义可以解释为:若可拓网络图中的两个物元结点R1和R2之间存在两条或两条以上的边,说明在知识库中存在对物元R1和R2不同的可拓展性描述,这种情况称之为可拓网络图的知识冲突.知识冲突会使可拓知识推理的元推理机在推理过程中混乱甚至意外中断.因此有必要对知识冲突进行消解.
定义4 对于可拓网络图G =<V, H >上的若干个物元结点R1, R2, …, Rm∈V, (m≤|V|),若任意一结点Ri(i=1, 2, …, m-1)都是结点Ri+1的前驱结点即Ri∈Proceed(Ri+1)(Proceed(Ri+1)表示结点Ri+1的前驱结点集),且Rm∈Procceed(R1),则认为可拓网络图G中存在路径冲突.
对于定义4的含义可以解释为:若可拓网络图出现环结构,说明可拓网络图中存在推理路径上的冲突,这种现象称之为路径冲突.路径冲突使可拓网络图形成一个不稳定无终止的动态系统,造成知识库系统中的元推理机无法找到推理的起始物元结点或经过有限步推理之后无法达到推理的终点,导致推理效率大大降低或者推理失败,因此必须对路径冲突进行消解.
根据定义3和定义4,判断可拓网络图中是否存在知识冲突或路径冲突,就是判断图中是否有多重边或环路.对于可拓网络图的两种冲突形式,本文给出了相应的冲突消解的规则:
规则1 对于定义3存在的知识冲突,采用“约束松弛原则”:对于可拓网络图G =<V, H >中任意两个物元结点R1和R2(R1, R2∈V),若边R1×R2→相关性及边R1×R2→蕴含性同时存在,取边R1×R2→相关性,舍弃边R1×R2→蕴含性.
规则1的提出是基于如下的考虑:物元的相关性和蕴含性所表现的知识形式是不同的.物元的相关性是指各物元之间的函数依赖关系并有公式相联系,它强调的是知识的逻辑性和理论性;而蕴含性是指各物元之间的相互依存关系,它强调的是知识的经验性.在两类知识发生冲突的时候,选择逻辑性更强的相关性知识.
规则2 对于定义4存在的路径冲突,采用“约束取消原则”:对环结构中冗余的、错误的或不重要的约束取消,进行解环.若在可拓网络图G =<V, H >中存在顶点集Γ={R1, R2, …, Rm}⊆V满足Ri∈Proceed(Ri+1)且Rm∈Procceed(R1),即Ri(i=1, 2, …, m-1)是Ri+1的前驱结点且Rm是R1的前驱结点,则去掉满足{<Ri, Ri+1>|Ri×Ri+1→蕴含性, deg+(Ri+1)≥2}(Ri, Ri+1∈Γ, i=1, 2, …, m-1)的边<Ri, Ri+1>,完成解环操作.
规则2的提出是基于如下的考虑:当可拓网络图存在环路时,对于在环路中的某个物元结点Ri+1,如果除了边<Ri, Ri+1>仍有环路之外的边与之相连,即deg+(Ri+1)≥2,则说明物元Ri+1并非完全依靠物元Ri来确定,因而可将环路中<Ri, Ri+1>去掉,完成解环操作.
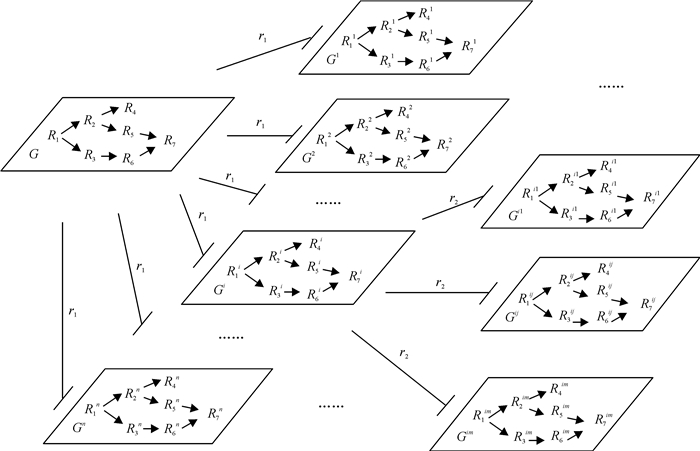
1.3 基于可拓网络图的设计方案形式化拓展在方案设计中,设计方案可以用一张可拓网络图来描述,设计参数相当于网络图中的物元结点,参数之间的内在联系可描述为各物元结点的可拓关系.方案拓展可以在可拓网络图的基础上,利用物元的各种发散性对可拓网络图的先驱结点进行发散推理实现.基于可拓网络图的设计方案形式化拓展原理可由如图 1所示.
|
图 1 设计方案的形式化拓展原理 Figure 1 Formalized principle of scheme extension |
在图 1中,假设G=<V, H>是由初始方案经过冲突消解的可拓网络图,V={R1, R2, …, R7}是初始方案重要参数构成的物元集合,H是参数之间的可拓关系集合.对G的先驱物元R1按照发散规则r1进行拓展可得到多个发散物元,即
规则3 R1┤{Rl1, Rl2, …Rli, Rln}.
再对发散后的物元进行相关性和蕴含性拓展即可得到拓展后的可拓网络图
规则4
进而拓展形成多个设计方案.利用物元的不同发散性r2规则,对拓展后的可拓网络图先驱物元结点进行二次发散,即R1┤{Rli1, Rli2, …Rlij, Rlim}(i=1, 2, …, n),进而对可拓网络图进行二次拓展,即
经过冲突消解之后的可拓网络图实际上是一种无环路有向简单图.在冲突消解后的可拓网络图上进行发散,就可以保证当前驱物元结点确定后,其后继结点可以唯一确定,避免了盲目发散带来的推理效率低下的问题.
2 设计方案的形式化拓展原理在智能系统中的实现 2.1 可拓继承推理基于可拓网络图的方案拓展需要足够的设计参数及其之间的可拓关系描述,而新产品往往缺乏这些描述.一般来说,新的设计都是对现有设计成果的继承和发展,因此设计领域广泛存在着产品的继承关系.为丰富可拓网络图对设计方案的描述,在方案拓展之前有必要对方案进行继承推理.可拓网络图是在物元及其可拓关系基础上构建的,因此可拓继承推理包括物元的继承和可拓关系的继承.物元的继承在文献[14]已经有详细描述.可拓关系也是构建可拓网络图的重要方面,对于两种继承关系AKO(A Kind Of)和ISA(IS A)的可拓关系继承,本文提出了3个主要定理:
定理1 已知物元R1=(A, c1, v1),R2=(B, c2, v2),若R1⇒R2且ISA(N, A),则有蕴含关系(N, c1, v1)⇒(B, c2, v2)
证明:用反证法.假设结论不成立,即(N, c1, v1)≠(B, c2, v2),即物元(N, c1, v1)存在的同时不能推出物元R2=(B, c2, v2)存在.根据形式逻辑的假言推理规则,若R1⇒R2,那么¬R2⇒¬R1.若R2=(B, c2, v2)不存在,可推出R1=(A, c1, v1)不存在.由形式逻辑的反三段论推演[16]可知,R1=(A, c1, v1)不存在且有ISA(N, A),可以推出物元(N, c1, v1)不存在,与条件矛盾.证毕.
定理2 已知物元R1=(A, c1, v1),R2=(B, c2, v2),若R1~R2且ISA(N, A),则有(N, c1, v1)~(B, c2, v2)
证明:由R1~R2及物元相关性的定义可知,c1(A)=f[c2(B)].由形式逻辑的三段论推演[17]法则,若R1=(A, c1, v1)存在且ISA(N, A),则(N, c1, v1)存在,即c1(A)=c1(N).由c1(A)=f[c2(B)]及c1(A)=c1(N)可知c1(N)=f[c2(B)],即(N, c1, v1)~(B, c2, v2).证毕.
定理3 已知物元R1=(A, c1, v1),R2=(B, c2, v2),若R1~R2且AKO(A1, A),则有(A1, c1, v1)~(B, c2, v2)
证明:由R1~R2及物元相关性的定义可知,c1(A)=f [c2(B)].由形式逻辑的三段论推演[16]法则,若R1=(A, c1, v1)存在且AKO(A1, A),则(A1, c1, v1)存在,即c1(A)=c1(A1).由c1(A)=f[c2(B)]及c1(A)=c1(A1)可知c1(A1)=f[c2(B)],即(A1, c1, v1)~(B, c2, v2).证毕.
2.2 设计方案拓展的知识推理算法相关性和蕴含性具有传递性,那么由相关图和蕴含图所组成的可拓网络图的结点可以构成拟序关系,对冲突消解后的可拓网络图进行拓扑排序.物元拓展推理的发散推理、相关推理和蕴含推理都在对可拓网络图拓扑排序基础上进行.基于可拓网络图的设计方案拓展知识推理算法如下:
算法 设计方案拓展知识推理算法
输入:知识库物元模型M
输出:拓展物元解集solutions
求解步骤:
(1) 对M进行可拓继承推理(定理1~定理3),得到拓展物元模型M′;
(2) 由知识库中的相关规则和蕴含规则,由M′构建可拓网络图G (定义1和定义2);
(3) 对图G进行冲突判定(定义3和定义4),若存在冲突则消解(规则1和规则2);
(4) 对图G进行边拓扑排序,结果入拟序规则队列Q;
(5) 若Q为空,则算法结束,否则从Q中取物元R1;
(6) 若R1在图G无前趋物元结点,则对R1进行发散推理(规则3),生成物元拓展解集solutions;
(7) 否则从图G中找到R1的前趋物元结点R2,由边<R2, R1>的信息对R1进行相关蕴含推理(规则4),推理结果添加到solutions;
(8) 返回(5).
对算法的有效性进行分析:由于发散的同时要对下游结点进行相关推理和蕴含推理,从而避免产生不合理的解;由于算法先对可拓网络图的物元顶点进行排序,即每次都是从当前图中的最上游物元顶点开始点发散,从而避免了算法的盲目发散.
3 水轮发电机参数预估的方案拓展过程水轮发电机的参数预估是按招标书给定的电机容量、电压、相数、频率、功率因数、转速等额定值来确定水轮发电机定子铁芯内径、外径、长度等基本尺寸的值或其范围.参数预估相当于方案设计的初始阶段,具有信息不完备性和多解性的特点[18].信息不完备性表现为水轮机参数预估的初始信息只有电站的招标数据,设计信息不完整、不确定,多解性表现在参数预估可生成多个初始设计方案,要求设计者在大量理论经验知识的基础上进行拓展思维,拓展出符合招标要求的设计方案,因此本文尝试采用基于可拓网络图的方案拓展知识推理进行参数预估设计.
根据水轮发电机的特点,可以确定水轮发电机的知识库物元模型如下:
| $ \left[{\begin{array}{*{20}{c}} {{\rm{水轮发电机Nz}}}&{额定功率{P_{\rm{a}}}({\rm{kW}})}&\phi &\mathit{\Phi} \\ {}&{额定功率因数\cos {\phi _{\rm{N}}}}&\phi &{{\rm{\{ 0}}{\rm{.8, 0}}{\rm{.85, 0}}{\rm{.875, 0}}{\rm{.9\} }}}\\ {}&{额定容量{S_{\rm{N}}}({\rm{kW}})}&\phi &\mathit{\Phi} \\ {}&{容量级别{\rm{Scale}}}&\phi &{{\rm{\{ 大容量, 中容量, 小容量\} }}}\\ {}&{额定频率f({\rm{Hz}})}&\phi &\mathit{\Phi} \\ {}&{额定电压{U_{\rm{N}}}({\rm{kV}})}&\phi &{{\rm{\{ 6}}{\rm{.3, 10}}{\rm{.5, 13}}{\rm{.8, 15}}{\rm{.75, 18, }} \cdots {\rm{\} }}}\\ {}&{额定转速{n_{\rm{N}}}({\rm{r/min}})}&\phi &\mathit{\Phi} \\ {}&{速度级别{\rm{Level}}}&\phi &{{\rm{\{ 高速, 中速, 低速\} }}}\\ {}&{飞逸转速{n_{\rm{r}}}({\rm{r/min}})}&\phi &\mathit{\Phi} \\ {}&{绕组形式{\rm{WType}}}&\phi &{{\rm{\{ 波绕组, 叠绕组\} }}}\\ {}&{结构型式{\rm{SType}}}&\phi &{{\rm{\{ 卧式, 立式\} }}}\\ {}&{极数2p}&\phi &\mathit{\Phi} \\ {}&{极距\tau ({\rm{cm}})}&\phi &\mathit{\Phi} \\ {}&{定子铁芯内径{D_{\rm{i}}}({\rm{cm}})}&\phi &\mathit{\Phi} \\ {}&{定子铁芯外径{D_{\rm{a}}}({\rm{cm}})}&\phi &\mathit{\Phi} \\ {}&{定子铁芯长度{l_{\rm{t}}}({\rm{cm}})}&\phi &\mathit{\Phi} \\ {}& \cdots & \cdots & \cdots \end{array}} \right] $ |
某电站水轮发电机招标参数如表 1所示.
| 表 1 某电站水轮发电机招标参数 Table 1 Bidding parameters of a hydro power plant |
根据表 1及继承关系ISA (某电站水轮发电机NzX,水轮发电机Nz),对该电站水轮发电机物元进行物元的继承推理,可以确定该电站水轮机知识库中的初始物元模型如下:
| $ \left[{\begin{array}{*{20}{c}} {{\rm{某电站水轮发电机NzX}}}&{额定功率{P_{\rm{a}}}({\rm{kW}})}& 2200 &\mathit{\Phi} \\ {}&{额定功率因数\cos {\phi _{\rm{N}}}}&0.8 &{{\rm{\{ 0}}{\rm{.8, 0}}{\rm{.85, 0}}{\rm{.875, 0}}{\rm{.9\} }}}\\ {}&{额定容量{S_{\rm{N}}}({\rm{kW}})}&\phi &\mathit{\Phi} \\ {}&{容量级别{\rm{Scale}}}&\phi &{{\rm{\{ 大容量, 中容量, 小容量\} }}}\\ {}&{额定频率f({\rm{Hz}})}&50 &\mathit{\Phi} \\ {}&{额定电压{U_{\rm{N}}}({\rm{kV}})}&6.3 &{{\rm{\{ 6}}{\rm{.3, 10}}{\rm{.5, 13}}{\rm{.8, 15}}{\rm{.75, 18, }} \cdots {\rm{\} }}}\\ {}&{额定转速{n_{\rm{N}}}({\rm{r/min}})}&125 &\mathit{\Phi} \\ {}&{速度级别{\rm{Level}}}&\phi &{{\rm{\{ 高速, 中速, 低速\} }}}\\ {}&{飞逸转速{n_{\rm{r}}}({\rm{r/min}})}&270 &\mathit{\Phi} \\ {}&{绕组形式{\rm{WType}}}&\phi &{{\rm{\{ 波绕组, 叠绕组\} }}}\\ {}&{结构型式{\rm{SType}}}&\phi &{{\rm{\{ 卧式, 立式\} }}}\\ {}&{极数2p}&\phi &\mathit{\Phi} \\ {}&{极距\tau ({\rm{cm}})}&\phi &\mathit{\Phi} \\ {}&{定子铁芯内径{D_{\rm{i}}}({\rm{cm}})}&\phi &\mathit{\Phi} \\ {}&{定子铁芯外径{D_{\rm{a}}}({\rm{cm}})}&\phi &\mathit{\Phi} \\ {}&{定子铁芯长度{l_{\rm{t}}}({\rm{cm}})}&\phi &\mathit{\Phi} \\ {}& \cdots & \cdots & \cdots \end{array}} \right] $ |
知识库中还记录了水轮发电机参数之间的关系,包含着大量有关水轮发电机的理论及实践知识,在知识库中以蕴含槽和相关槽的形式来描述,部分规则如表 2和表 3所示.
| 表 2 水轮发电机设计蕴含规则 Table 2 Implement ation rules for the hydro design |
| 表 3 水轮发电机设计相关规则 Table 3 Correlative rules for the hydro design |
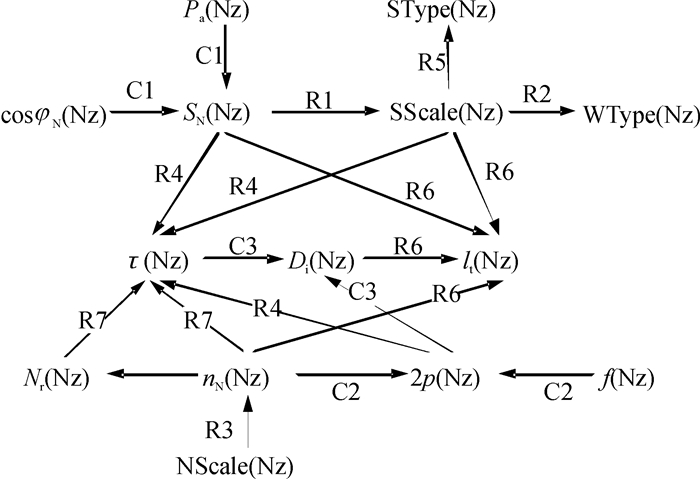
根据继承关系ISA (某电站水轮发电机NzX,水轮发电机Nz)以及水轮发电机Nz对相关性和蕴含性在知识库中的描述,对该电站水轮发电机进行可拓关系的继承推理,生成某电站水轮发电机NzX的可拓网络图,如图 2所示.
|
图 2 水轮发电机可拓网络图 Figure 2 Extension network of the hydro design |
对图 2的可拓网络图进行冲突判定,发现没有冲突.对可拓约束图进行拓扑排序,可得到可拓推理规则的拟序集合.拟序集就确定了推理规则的应用前后顺序,下面是合理拟序集之一:
POrder(rules,<)={C1, C2, R3, C4, R1, R2, R4, R7, R5, C3, R6}.
按照拟序集中的规则队列对某电站进行相关蕴含推理,并在推理过程中融入了区间代数思想,可得到如下的推理结果:
| $ $ \[\left[{\begin{array}{*{20}{c}} {{\rm{某电站水轮发电机NzX}}}&{额定功率{P_{\rm{a}}}({\rm{kW}})}& 2200 &\mathit{\Phi} \\ {}&{额定功率因数\cos {\phi _{\rm{N}}}}&0.8 &{{\rm{\{ 0}}{\rm{.8, 0}}{\rm{.85, 0}}{\rm{.875, 0}}{\rm{.9\} }}}\\ {}&{额定容量{S_{\rm{N}}}({\rm{kW}})}&2\;750 &\mathit{\Phi} \\ {}&{容量级别{\rm{Scale}}}& 中容量 &{{\rm{\{ 大容量, 中容量, 小容量\} }}}\\ {}&{额定频率f({\rm{Hz}})}&50 &\mathit{\Phi} \\ {}&{额定电压{U_{\rm{N}}}({\rm{kV}})}&6.3 &{{\rm{\{ 6}}{\rm{.3, 10}}{\rm{.5, 13}}{\rm{.8, 15}}{\rm{.75, 18, }} \cdots {\rm{\} }}}\\ {}&{额定转速{n_{\rm{N}}}({\rm{r/min}})}&125 &[0, 375] \\ {}&{速度级别{\rm{Level}}}&低速 &{{\rm{\{ 高速, 中速, 低速\} }}}\\ {}&{飞逸转速{n_{\rm{r}}}({\rm{r/min}})}&270 &[250, 287.5] \\ {}&{绕组形式{\rm{WType}}}&叠绕组 &{{\rm{\{ 波绕组, 叠绕组\} }}}\\ {}&{结构型式{\rm{SType}}}&立式 &{{\rm{\{ 卧式, 立式\} }}}\\ {}&{极数2p}& 48 &\mathit{\Phi} \\ {}&{极距\tau ({\rm{cm}})}&\phi &[15.704, 58.437] \\ {}&{定子铁芯内径{D_{\rm{i}}}({\rm{cm}})}&\phi & [239.94, 892.85] \\ {}&{定子铁芯外径{D_{\rm{a}}}({\rm{cm}})}&\phi &[257.371 4, 965.896 3] \\ {}&{定子铁芯长度{l_{\rm{t}}}({\rm{cm}})}&\phi &[23.446, 262.965 2] \\ {}& \cdots & \cdots & \cdots \end{array}} \right]\] $ $ |
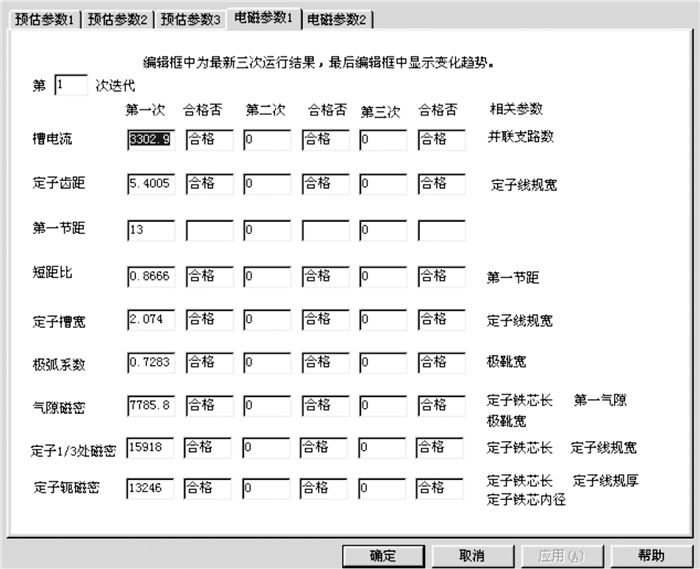
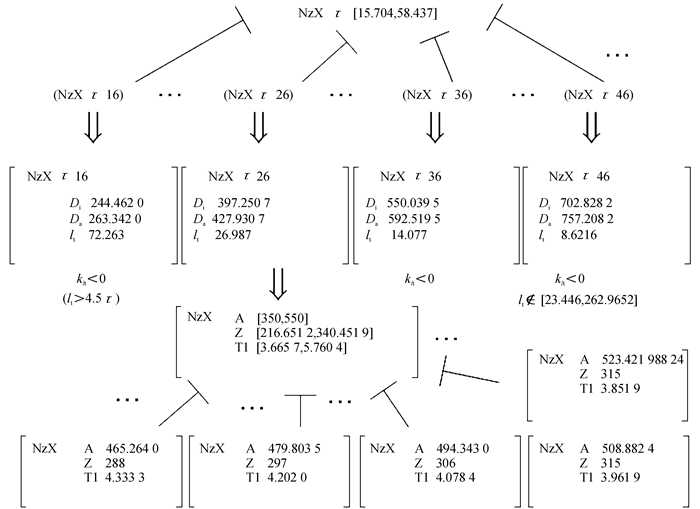
由此阶段推理结果可看出,定子铁芯内径Di、定子铁芯外径Da及定子铁芯长度lt的值仍未确定,此三个特征是水轮发电机的重要特征,后续的电磁设计大部分的参数都由此三个特征元来确定.对此三个物元在其量域内进行发散推理得到了多个初始设计方案,如图 3和图 4所示.
|
图 3 水轮发电机的参数预估界面 Figure 3 Interface of the hydro parameter estimate |
|
图 4 水轮发电机参数预估过程方案拓展 Figure 4 Scheme extension of the hydro parameter estimate |
如果单纯靠设计人员设计,只能根据以往经验计算出4-5种方案综合比较后给出最合适方案.通过计算机进行方案拓展,可以得到800多种设计方案.将800多个初始方案根据设计要求进行优度评价[19],并根据国家及企业标准对参数进行修正后,得到了最终的参数预估方案.
| $ $ \[\left[{\begin{array}{*{20}{c}} {{\rm{某电站水轮发电机NzX}}}&{额定功率{P_{\rm{a}}}({\rm{kW}})}& 2200 &[500, 10 000] \\ {}&{额定功率因数\cos {\phi _{\rm{N}}}}&0.8 &{{\rm{\{ 0}}{\rm{.8, 0}}{\rm{.85, 0}}{\rm{.875, 0}}{\rm{.9\} }}}\\ {}&{额定频率f({\rm{Hz}})}&50 & \\ {}&{额定电压{U_{\rm{N}}}({\rm{kV}})}&6.3 &{{\rm{\{ 6}}{\rm{.3, 10}}{\rm{.5, 13}}{\rm{.8, 15}}{\rm{.75, 18, }} \cdots {\rm{\} }}}\\ {}&{额定转速{n_{\rm{N}}}({\rm{r/min}})}&125 &[0, 375] \\ {}&{飞逸转速{n_{\rm{r}}}({\rm{r/min}})}&270 &[250, 287.5] \\ {}&{定子铁芯内径{D_{\rm{i}}}({\rm{cm}})}&390 & [239.94, 892.85] \\ {}&{定子铁芯外径{D_{\rm{a}}}({\rm{cm}})}&425 &[257.371 4, 965.896 3] \\ {}&{定子铁芯长度{l_{\rm{t}}}({\rm{cm}})}&28 &[23.446, 262.965 2] \\ {}&定子槽数{\rm{Z}} & 306 & [216.651 2, 340.451 9] \\ {}& \cdots & \cdots & \cdots \end{array}} \right]\] $ $ |
此方案为全新设计方案,并不在以往设计方案实例库中.由此可见,利用计算机实现拓展思维可以充分利用计算机速度快、存储量大的特点推理出更多可供选择的设计方案,也更有可能得到最适合的设计方案.
4 结语本文尝试将拓展思维形式化实现于智能系统中,提出了基于可拓网络图的设计方案形式化拓展原理,给出了设计方案的形式化拓展知识推理算法,并将其应用于水轮发电机的参数预估.本文主要结论如下:
(1) 通过定义物元的可拓关系建立了可拓网络图,使知识库中的可拓推理规则有效整合,成为有机整体;
(2) 在可拓网络图基础上分析冲突并进行消解,使可拓网络图成为无环路的有向简单图,避免了推理的重复和混乱;
(3) 在冲突消解的可拓网络图上进行可拓推理,以发散推理为动力带动相关和蕴含推理,有效组织了可拓推理规则的实施运用,以发散推理为动力充分体现了创新构思的过程;
(4) 提出了物元的可拓展性继承,包括相关性和蕴含性的继承推理,并将可拓继承推理整合到基于可拓网络图的知识推理系统中;
(5) 目前在方案设计中对原始方案的拓展大多依靠人的创造性劳动,对于复杂产品来说增加了设计人员的难度,按照上述方法进行设计方案的拓展,以得到更多的设计方案,从而更有可能得到最合适的设计结果.
| [1] |
Roberto V. Design-Driven Innovation: Changing the Rules of Competition by Radically Innovating What Things Mean[M]. Boston: Harvard Business Press, 2009.
|
| [2] |
Sharma R, Gao J X. A knowledge-based manufacturing and cost evaluation system for product design /re-design[J].
International Journal of Advanced Manufacturing Technology, 2007, 33(9-10): 856-865.
DOI: 10.1007/s00170-006-0530-6. |
| [3] |
Jiang H, Yen C C. Design Thinking in Conceptual Design Processes: A Comparison Between Industrial and Engineering Design Students[C]// Coelho D A. Advances in Industrial Design Engineering. Closter: InTech, 2013: 29-46.
|
| [4] |
Guilford J P. Creative abilities in the arts[J].
Psychological Review, 1957, 64(2): 110-118.
DOI: 10.1037/h0048280. |
| [5] |
钱学森. 关于思维科学[J].
自然杂志, 1983, 6(8): 563-572.
Qian X S. About thinking science[J]. Nature Magazine, 1983, 6(8): 563-572. |
| [6] |
吴文俊, 李幼平. "可拓论及其应用"鉴定意见[EB/OL]. http://web.gdut.edu.cn/~extenics/pingjia1.htm, [2013-06-05].
|
| [7] |
蔡文, 杨春燕, 何斌. 可拓学研究中的若干问题[J].
广东工业大学学报, 2001, 18(1): 1-5.
Cai W, Yang C Y, He B. Several problems on the research of Extenics[J]. Journal of Guangdong University of Technology, 2001, 18(1): 1-5. |
| [8] |
杨春燕. 新产品构思的第三创造法[J].
广东工业大学学报, 1997, 14(1): 21-26.
Yang C Y. Third way of creation in new product design[J]. Journal of Guangdong University of Technology, 1997, 14(1): 21-26. |
| [9] |
赵燕伟. 基于多级菱形思维模型的方案设计新方法[J].
中国机械工程, 2000, 11(6): 684-686.
Zhao Y W. A new method for scheme design based on the multilevel rhombus thought models[J]. China Mechanical Engineering, 2000, 11(6): 684-686. |
| [10] |
刘晓平, 秦晋. 创新设计中的物元的知识表示方法[J].
工程图学学报, 2006, 27(6): 31-35.
Liu X P, Qin J. Comparison different knowledge representation in innovation design[J]. Journal of Engineering Graphics, 2006, 27(6): 31-35. |
| [11] |
钟诗胜, 张艳. 可拓知识表示及知识库系统的开发[J].
计算机集成制造系统, 2008, 14(11): 2184-2190.
Zhong S S, Zhang Y. Extension-based knowledge representation and development of knowledge base system[J]. Computer Integrated Manufacturing System, 2008, 14(11): 2184-2190. |
| [12] |
杜春彦. 可拓推理[J].
广东工业大学学报, 1999, 16(2): 105-108.
Du C Y. Extension reasoning[J]. Journal of Guangdong University of Technology, 1999, 16(2): 105-108. |
| [13] |
陈文伟, 杨春燕, 黄金才. 可拓知识与可拓知识推理[J].
哈尔滨工业大学学报, 2006, 38(7): 1094-1096.
Chen W W, Yang C Y, Huang J C. Extension knowledge and Extension knowledge reasoning[J]. Journal of Harbin Institute of Technology, 2006, 38(7): 1094-1096. |
| [14] |
杨国为, 卢兴华, 涂序彦. ICAD中概念设计的物元系统与或网模型及相关可拓推理[J].
计算机工程, 2004, 30(17): 29-30.
Yang G W, Lu X H, Tu X Y. AND/OR net model of matter element system for concept design and related extension reasoning[J]. Computer Engineering, 2004, 30(17): 29-30. DOI: 10.3969/j.issn.1000-3428.2004.17.013. |
| [15] |
蔡文, 杨春燕, 何斌.
可拓逻辑初步[M]. 北京: 科学出版社, 2003.
|
| [16] |
田粟. 从反三段论看三段论及假言推理[J].
西南政法大学学报, 2000, 2(1): 16-19.
Tian S. Look at syllogism and hypothetical syllogism from anti-syllogism[J]. Journal Southwest University of Political Science and Law, 2000, 2(1): 16-19. |
| [17] |
Patzig G. Aristotle's theory of the syllogism: A Logico-Philological Study of Book a of the Prior Analytics[M]. Dordrecht: D. Reidel Publishing Company, 1968.
|
| [18] |
Xie X, Lin L, Zhong S. Handling missing values and unmatched features in CBR system for hydro-generator design[J].
Computer-Aided Design, 2013, 45(6): 963-976.
DOI: 10.1016/j.cad.2013.02.004. |
| [19] |
李仁旺, 彭卫平, 顾新建, 等. 可拓学中优度评价方法在变型设计中的应用研究[J].
计算机集成制造系统, 2001, 7(4): 48-51.
Li R W, Peng W P, Gu X J, et al. Study on goodness evaluation method in extenics and its application in the variant design[J]. Computer Integrated Manufacturing Systems, 2001, 7(4): 48-51. |
 2014, Vol. 31
2014, Vol. 31