无线传感器网络[1](Wireless Sensor Network,WSN)是一种在特定区域内随机投放或者安置大量传感器节点所形成的网络.无线传感器网络节点的电量十分有限[2-3],并难以更换或者补充.如何有效利用节点能量,延长网络寿命已经成为研究人员的首要目标[4].近几年,针对传感器网络簇选节点的能量问题,一些学者提出将剩余能量作为簇选的参考因子.如在LEACH[5-7]算法基础上提出的经典的改进算法HEED[8],其在簇头选择标准以及簇头竞争机制上与LEACH算法不同,成簇速度有一定的改进,特别是考虑成簇后簇内的通信开销,把节点剩余能量作为一个参数,使得选出的簇头更适合担当数据转发任务.但上述算法没有考虑节点能量损耗的快慢,在一定程度上不能有效降低节点的死亡时间.
提出了一种基于能量比的簇首选择机制BECS(Cluster-head Selection Mechanism Based on Energy Ratio).一定程度上缓解了网络中节点过早死亡的问题,可有效延长网络的生命周期.
1 LEACH算法简介经典的自适应分簇拓扑(Low Energy Adaptive Clustering Hierarchy, LEACH)算法能够等概率选取节点来担任簇头,保证网络中节点的能量消耗相对均衡[9].
LEACH算法在选举簇头时,首先有节点Nodei产生随机数Nodeinum,如果Nodeinum < T(n),则发布公告消息Messageicluster,表示节点Nodei成为簇头Nodei_cluster.新一轮循环中,节点的NodeiT(n)=0时,Nodei被放弃再次当选为簇头.剩余节点则将以T(n)阈值当选;随着节点中NodeiT(n)=0的节点比例增加,使得阈值T(n)增大,这样Nodei产生的Nodeinum小于T(n)的概率便增大,最后增大了剩余节点当选簇头的概率.本文根据文献[10]可知T(n)的表达式为
| $ T\left( n \right) = \left\{ \begin{array}{l} \frac{p}{{1 - p \times \left[ {r\bmod \left( {\frac{1}{p}} \right)} \right]}},n \in G,\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他. \end{array} \right. $ | (1) |
式(1)在选举簇头的时候并没有考虑到节点的剩余能量因子.
本文提出一种基于能量代价的能量比簇首选择算法.提出了能量比概念,将能量值转化为节点能耗快慢的量度,并结合剩余能量与网络的簇内平均能量选择簇头节点.仿真结果表明,本文BECS算法在延长网络的生命周期,增加网络收集的数据量方面比LEACH算法更有优势.
2 系统模型本文采用的系统模型为:设定M×M的区域内随机投放N个位置固定的传感器节点.传感器网络具有以下性质[11]:(1)网络是静态的网络,所有的传感器节点在被安置或者随机投放之后就静止不动.(2)网络中任一节点的初始能量NodeiE0以及发射功率NodeiW都相等.(3)网络任何相邻节点所监测、收集的数据NodeiData具有相似可融性.(4)如果节点发射功率为Nodei_jW,接收节点则能利用接收信号的强度[12]Nodei_jRSSI计算出节点之间的近似距离Distanceij.(5)节点可感知自己的剩余能量Ei_rest.
本文算法采用文献[5]所用的能耗模型,该模型与Leach算法采用的能耗模型相同.传感器节点发送l比特数据到距离d的位置所消耗的能量为
| $ \begin{array}{l} {E_{{\rm{Tx}}}}\left( {l,d} \right) = \\ {E_{{\rm{Tx\_elec}}}}\left( l \right) + {E_{{\rm{Rx\_amp}}}} = \left\{ \begin{array}{l} l{E_{{\rm{elec}}}} + l{\varepsilon _{{\rm{fs}}}}{d^2},d \le {d_0},\\ l{E_{{\rm{elec}}}} + l{\varepsilon _{{\rm{amp}}}}{d^4},d > {d_0}, \end{array} \right. \end{array} $ | (2) |
| $ {E_{{\rm{Rx}}}}\left( l \right) = {E_{{\rm{Rx\_elec}}}}\left( l \right) = l{E_{{\rm{elec}}}}, $ | (3) |
式中,ETx(l, d)表示发送端的能量消耗,ERx(l)表示接收端的能量消耗,Eelec表示节点发送或者接收每比特数据的能量消耗,εfsd2和εampd4是放大器的能量消耗,εfs和εamp分别是自由空间传播模型和多径衰减传播模型的能量消耗.
基于能量消耗比的簇首选择机制综合了网络中节点的剩余能量和节点与节点之间的传输能量s损耗来进行簇首的选择.例如,无线传感器网络中的需要重新选择簇头进行分簇,簇头在簇内可以收集簇内节点的能量参数,包括节点剩余能量Ei_rest,节点发送数据消耗的能量Ei_Tx(k, d),节点接收数据消耗的能量Ei_Rx(k)等.本文算法根据节点与基站的距离,决定选择多跳传输或者直接传输[14],因此,d表示为普通节点距离基站的距离或与下一跳节点的距离.算法引入能量比概念,参考节点的能量消耗的代价比值,选择更加合理、高效的节点当选簇头.
能量比ec,定义表示节点在网络运行若干周期之后,下一个网络周期运行之前,节点的剩余能量值与节点预算成为簇内节点并稳定运行时所需要产生的必要能量消耗值,两值之间形成的参数值.参考式(4).
第一种情况,仅考虑节点的剩余能量时,如果节点Nodei的Ei_rest大于节点Nodej的Ej_rest,节点Nodei则当选下一轮簇头节点.下面考虑另外一种情况:节点Nodei的剩余能量值为Ei_rest,节点Nodej的剩余能量为Ej_rest,其中Ei_rest > Ej_rest.节点Nodei当选簇头网络运行一个周期需要消耗的能量值为Ei_take,节点Nodej需要Ej_take,其中Ei_take > Ej_take.从而可以得到一个这样的计算结果Ei_rest/Ei_take与Ej_rest/Ej_take,且前者小于后者.因此,表明节点Nodej当选簇头更具有合理性.其中涉及的相关能量比公式定义如下:
| $ {e_{i\_c}} = \sqrt[a]{{{E_{i{\rm{\_rest}}}}/{E_{i{\rm{\_take}}}}}}, $ | (4) |
| $ {E_{i{\rm{\_take}}}} = {E_{i{\rm{\_Tx}}}}\left( {k,d} \right) + {E_{i{\rm{\_Rx}}}}\left( {\rm{k}} \right) + {E_{i{\rm{\_}}DA}}\left( k \right), $ | (5) |
| $ {E_{i{\rm{\_DA}}}}\left( k \right) = k{E_{{\rm{DA}}}}, $ | (6) |
其中,ei_c表示节点Nodei的能量比,a表示能量比梯度,根据网络中能量比的有效性进行调节,a的实验取值范围为1~6,EDA表示传感器节点处理每比特数据需要消耗的能量,Ei_DA(k)则为传感器节点处理k比特数据的能耗.
针对无线传感器网络中簇的形成可由3部分组成:
(1) 簇首数目的确定.
分簇路由算法中,簇的数目影响着算法性能[15].因此,网络必须合理地确定簇的数目,使得网络的能量消耗更加均衡,从而提高网络的性能.假设存在k个分簇,由N个节点组成的一个无线传感器网络,其分布的区域大小为M×M.并且每个簇群的能耗主要包括接收簇内节点发送的数据消耗的能量、融合处理所接收的数据所消耗的能量,将融合处理的数据发送给基站消耗的能量,根据文献[16]有
| $ {E_{{\rm{take}}}} = {E_{{\rm{send}}}} + {E_{{\rm{DA}}}} + {E_{{\rm{trans}}}}. $ | (7) |
根据式(7)变形可得网络能量消耗关于k的函数值,并求导可得分簇个数的最佳期望值kopt为
| $ {k_{{\rm{opt}}}} = \sqrt {\frac{{{M^2}N}}{{2{\rm{ \mathsf{ π} }}}}} \sqrt {\frac{{{\varepsilon _{fs}}}}{{2\left( {n - 1} \right)\left( {{E_{{\rm{elec}}}} + {E_{DA}}} \right) - {E_{{\rm{elec}}}} + n{\varepsilon _{{\rm{fs}}}}{\gamma ^2}}}} , $ | (8) |
其中,γ的范围需要根据簇群簇头节点采用多跳转发消息消耗能量小于直接转发消息到基站消耗的条件确定.
(2) 簇首选择.
BECS算法的关键在于提出能量比,将能量比作为选择簇头的参考因子,在每一轮的网络簇头选择时,将具有较大的能量比的节点作为簇头的候选节点.与此同时,算法也考虑节点的剩余能量.因而,在阈值T(i)的计算过程中将两者作为计算参数,T(i)的计算公式为
| $ T\left( i \right) = \left\{ \begin{array}{l} \frac{{p\left( i \right)}}{{1 - p\left( i \right) \times \left[ {\bmod \left( {\frac{1}{{p\left( i \right)}}} \right)} \right]}} \times \frac{{{E_{i{\rm{\_rest}}}}}}{{{E_0}}},n \in G,\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他, \end{array} \right. $ | (9) |
| $ p\left( i \right) = {e_{i{\rm{\_}}c}} \times \frac{m}{{\sum\limits_{x = 1}^n {{e_{x{\rm{\_}}c}} - \left( {n - m} \right){e_{{\rm{Pre}}}}} }}. $ | (10) |
式(9)中Ei_rest表示节点的剩余能量,E0表示节点能量的初始值,大小等于NodeiE0.式(10)中m的大小表示网络经过r轮次之后未当选过簇头的普通节点个数,ePre表示前r轮中所有当选过簇头的节点的平均能量比值.由此可以看出,节点ei_c值较大的节点将优先考虑,并且考虑节点的剩余能量,Ei_rest较大阈值将会变大,相反,Ei_rest较小则阈值就相应变小.
(3) 簇的形成.
当选为簇首的节点Nodei_cluster,在网内发布Messageicluster消息,广播其成为了簇首,其余的网络节点则比较所接收到不同簇首的Messageicluster的信号强度Nodei_jRSSI选簇,并给选定的Nodei_cluster发送一条JoinMessagei_jcluster表示加入Nodei_cluster,簇首则根据JoinMessagei_jcluster进行簇的建立,完成后就为簇内节点安排调度数据发送的时分多址时隙表,簇内节点通过接收广播接收.最后,网络中不同的簇快速形成,各簇则主要以完成数据采集、传输、处理为目的而稳定运行.
4 仿真与分析为了评价和分析本文BECS算法的性能,作者采用Matlab 7.11.0仿真软件将算法进行相关的仿真实验.与此同时,在相同的初始条件下对LEACH算法以及FBECS算法进行了仿真实验.FBECS算法考虑节点相关能量对簇首选择影响,而不考虑能量比因子的作用,与BECS算法形成一定的对比.仿真实验中,将100个传感器节点随机投放在大小设定为100 m×100 m的实验场景区域.如图 1所示.

|
图 1 WSN节点随机分布 Figure 1 WSN nodes randomly distributed |
并将基站的坐标设置为(50 m,100 m),在本次实验中γ的取值选择小于100 m适合于单跳比较节约能量.实验中采用的主要相关参数以及参数值如表 1所示.
| 表 1 仿真参数表 Table 1 Parameters used in simulation |
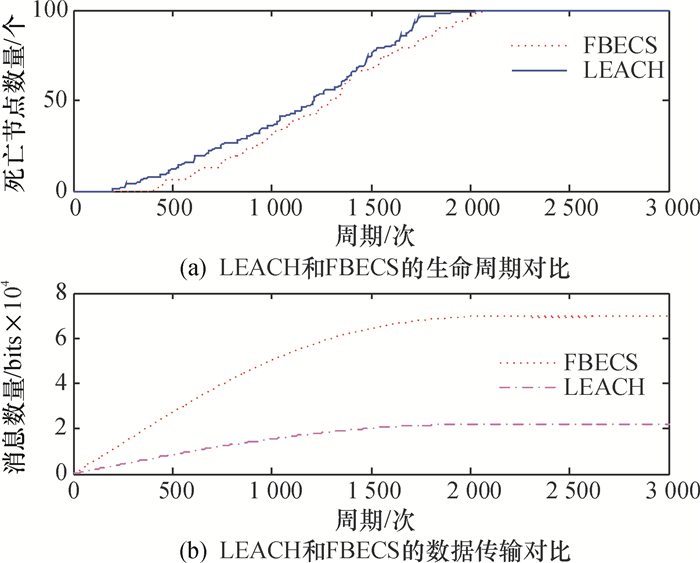
图 2是LEACH算法和FBECS算法仿真实验结果图,分别表现的是两种算法的存活节点数目随网络周期变化生成的曲线图,以及基站从网络中接收的累积数据总量随网络周期变化生成的曲线图.FBECS算法中p(i)取值的为0.05,并不考虑能量比因子.从图 2中可以得出FEBCS算法中处于死亡状态的首个节点的时间点和最后死亡节点的时间点都大于LEACH算法中处于死亡状态的首节点与最后节点的时间点,整个网络的生命周期提高了2%,基站接收的数据总量也提高了0.25倍的关系.
|
图 2 L网络与F网络相关参数曲线变化 Figure 2 L and F network-related parameter curves |
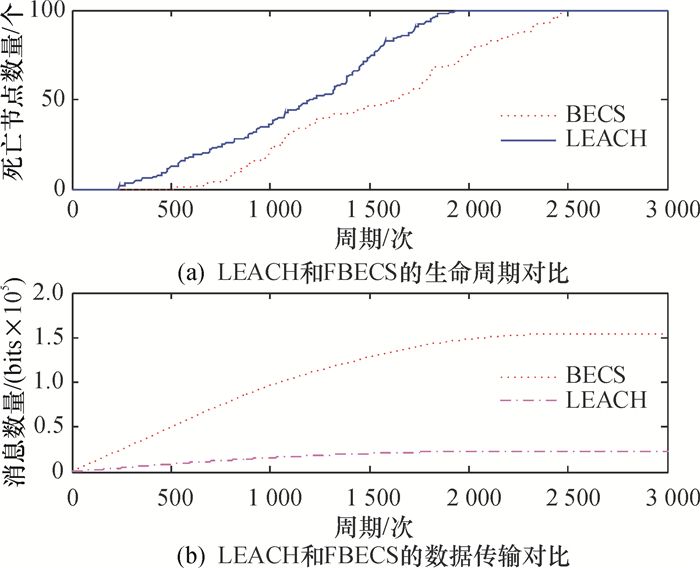
图 3是LEACH算法和BECS算法仿真实验对比图,该图的数据表明了BECS算法较LEACH算法在时间周期轮数与基站累积数据量上存在明显的优势.如,两种算法从死亡的首个节点和最后节点比较,BECS算法生存的时间周期明显大于LEACH算法的生存时间;通过多组实验统计,网络利用BECS算法,其生存时间平均可提高超过网络利用LEACH算法生存时间的20%.因此,传感网络的有效工作寿命得到有效延长.
|
图 3 L网络与B网络相关参数曲线变化 Figure 3 L and B network-related parameter curves |
图 3中显示截止到2 500个周期以后,网络分别对LEACH算法与BECS算法的应用,基站接收数据总量存在很大的差异;据计算BECS算法使得基站接收的数据总量平均可提高0.75倍.由于BECS算法提出能量比概念,一定范围内考虑了数据传输在传输路径上存在能量消耗的比例关系;并将这种关系定义为节点对剩余能量消耗的代价值,可直观地监测网络中节点的能量消耗的快慢度.所以,BECS算法能缓慢网络中的能量消耗,有效提高网络的性能.
5 结束语本文通过对经典LEACH算法的优缺点的分析,提出了一种基于节点能量比的簇选算法BECS,该算法结合簇建立阶段通信能量的损耗,计算出最优簇头数目,并选择剩余能量与能量比两个因素最优,选取能量代价更小的节点作为更加合理的簇头.仿真实验验证BECS算法簇选机制的可行性;与LEACH算法相比,BECS算法的网络生命周期与网络接收的数据总量在LEACH算法的基础上分别提高了20%与0.75倍,有效延长了传感器网络的生命周期.
| [1] |
崔莉, 鞠海玲, 苗勇, 等. 无线传感器网络研究进展[J].
计算机研究与发展, 2005, 42(1): 163-174.
Cui L, Ju H L, Miao Yong, et al. Advances in wireless sensor networks[J]. Computer Research and Development, 2005, 42(1): 163-174. |
| [2] |
Liu T, Peng J, Wang J Z, et al. Data delivery scheme of delay tolerant mobile sensor network based on node priority[J].
Computer Science, 2011, 38(3): 140-143.
|
| [3] |
Ren F Y, Huang H N, Lin C. Wireless sensor networks[J].
Journal of Software, 2003, 14(7): 1282-1291.
|
| [4] |
Qing L, Zhu Q X, Wang M W. A distributed energy-efficient clustering algorithm for heterogeneous wireless sensor net-works[J].
Journal of Software, 2006, 17(3): 1282-1291.
|
| [5] |
Doshi S, Bhandare S, Brown T. An on-demand minimum energy routing protocol for a wireless ad hoc net-work[J].
ACM SIGMO-BILE Mobile Computing and Communications Review, 2002, 6(3): 50-66.
DOI: 10.1145/581291. |
| [6] |
Kwan-Wu Chin, Pair Wise. A time hopping medium access control protocol for wireless sensor networks[J].
IEEE Transactions on Consumer Electronics, 2009, 55(4): 1898-1906.
DOI: 10.1109/TCE.2009.5373748. |
| [7] |
Nizar Bouabdallah, Mario E Rivero-Angeles, Bryno Sericola. Continuous monitoring using event driven reporting for cluster-based wireless sensor networks[J].
IEEE Transactions on Vehicular Technology, 2009, 58(7): 3460-3479.
DOI: 10.1109/TVT.2009.2015330. |
| [8] |
王秀花, 张国荣. 无线传感器网络中基于Heed算法的多层分簇路由算法[J].
甘肃联合大学学报, 2011, 25(1): 78-81.
Wang X H, Zhang G R. Wireless sensor network routing algorithm based clustering algorithm for multi Heed[J]. Journal of Gansu Lianhe University, 2011, 25(1): 78-81. |
| [9] |
彭越, 吴多龙, GuillaumeAndrieux, 等. 基于最小能量法的无线传感器网络节点能量有效性研究[J].
广东工业大学学报, 2014, 31(1): 86-89.
Peng Y, Wu D L, Guillaume Andrieux, et al. Research on energy-efficiency in wireless sensor networks based on minimum energy coding[J]. Journal of Guangdong University of Technology, 2014, 31(1): 86-89. |
| [10] |
孙利民, 李建中, 陈渝, 等.
无线传感器网络[M]. 北京: 清华大学出版社, 2005.
|
| [11] |
姚光顺, 温卫敏, 张永定, 等. 改进的无线传感器网络簇首选择策略及其路由算法[J].
计算机应用, 2013, 33(4): 908-911, 915.
Yao G S, Wen W M, Zhang Y D, et al. Improved wireless sensor network cluster head selection policy and routing algorithm[J]. Journal of Computer Application, 2013, 33(4): 908-911, 915. |
| [12] |
曹建玲, 陈永超, 任智, 等. 基于多轮分簇的无线传感器网络路由协议[J].
计算机科学, 2013, 40(7): 67-70, 97.
Cao J L, Chen Y C, Ren Z, et al. Of multiple rounds of the cluster-based routing protocol for wireless sensor networks[J]. Computer Science, 2013, 40(7): 67-70, 97. |
| [13] |
李洪兵, 熊庆宇, 石为人. 无线传感器网络非均匀等级分簇拓扑结构研究[J].
计算机科学, 2013, 40(2): 49-52, 77.
Li H B, Xiong Q Y, Shi W R. Heterogeneous hierarchical clustering in wireless sensor networks topology research[J]. Computer Science, 2013, 40(2): 49-52, 77. |
| [14] |
吕涛, 朱清新, 朱玉玉. 一种能耗均衡的无线传感器网络分簇算法[J].
计算机应用, 2012, 32(11): 3107-3111.
Lü T, Zhu Q X, Zhu Y Y. An energy balance algorithm for clustering in wireless sensor networks[J]. Journal of Computer Application, 2012, 32(11): 3107-3111. |
| [15] |
蔡海滨, 琚小明, 曹奇英. 多级能量异构无线传感器网络的能量预测和可靠局促路由协议[J].
计算机学报, 2009, 32(12): 2394-2402.
Cai H B, Ju X M, Cao Q Y. Multiple levels of energy and reliable projections of energy cramped in heterogeneous wireless sensor network routing protocol[J]. Chinese Journal of Computer, 2009, 32(12): 2394-2402. |
| [16] |
李玲, 王林, 张飞鸽, 等. 无线传感器网络低功耗自适应分簇协议[J].
计算机应用, 2012, 32(10): 2700-2703.
Li L, Wang L, Zhang F G, et al. Low power adaptive clustering protocol for wireless sensor networks[J]. Journal of Computer Application, 2012, 32(10): 2700-2703. |
 2014, Vol. 31
2014, Vol. 31