2. 广东石油化工学院 电子与计算机学院,广东 茂名 525000;
3. 广东省石化装备故障诊断重点实验室,广东 茂名 525000
2. School of Electronic Information and Computer, Guangdong University of Petrochemical Technology, Maoming 525000, China;
3. Guangdong Key Laboratory of Petrochemical Equipment Fault Diagnosis, Maoming 525000, China
近年来,云计算[1-2]成为了工业界和学术界研究热点.云计算是并行计算、网格计算[3]的发展,属于分布式计算的一种技术,核心思想是将大量用网络连接起来的计算资源进行统一管理和调度,形成一个计算资源池向用户提供服务.提供这种资源的网络被称为“云”.云计算的任务调度问题属于一个新兴课题,现有的一些理论还不够完善,缺乏一个系统的方法.近年兴起的启发式智能化方法引起了众多学者的关注和兴趣,诸如模拟退火、神经网络、遗传算法、微粒群算法、蚁群算法,以及它们之间的混合算法[4-7],这些算法成为解决NP类以及组合爆炸问题的有力工具.文献[8]提出了一种具有双适应度的遗传算法(DFGA),在保证任务的总完成时间最小的情况下,也考虑到任务的平均完成时间,然而该类算法对系统中的反馈信息利用不够充分,求解效率低;文献[9]提出一种基于蚁群优化的计算资源分配算法,根据云环境的特点,分析了诸如线路质量、带宽占用和响应时间等因素对调度的影响;文献[10]提出了一种改进的蚁群算法,算法在达到整体网络负载均衡的同时,还延长网络寿命并获得利润.由于蚁群算法初始阶段缺乏信息素,存在搜索时间过长、易于停滞的缺点,因此在搜索效率上不高.文献[11]提出了基于信任驱动的资源负载均衡调度算法.该算法不仅考虑了用户任务的信任需求,目标是使资源达到负载平衡,而且兼顾任务执行时间跨度等因素.本文在充分利用“云”资源前提下,对云计算中任务的高效合理调度和资源的负载均衡机制进行了研究,提出了一种基于蚁群模拟退火算法(ACOSA)的任务调度算法,并通过仿真实验,验证了云环境下该算法具有良好的任务调度性能.
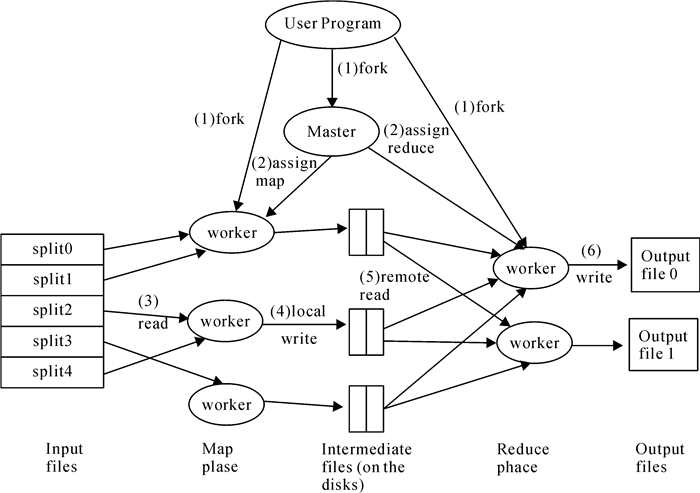
1 问题描述 1.1 云计算中的编程模型目前的云环境中使用的计算模式[12]很多都是采用谷歌公司提出的MapReduce,该模型将每个任务分成若干个子任务,然后把子任务调度到大规模的虚拟机计算节点中进行处理.MapReduce非常适合对大规模数据集的处理.其执行过程如图 1所示.
|
图 1 MapReduce的具体执行过程 Figure 1 The specific implementation process of MapReduce |
从图 1可看出,MapReduce有6个步骤,经分析可分成两个主要的过程:(1) Map过程:把每个任务由程序里MapReduce库分割成M个片,每个片大小从16到64MB不等;进而分配给多个worker并行执行,输出经过处理后得出的中间结果;(2) Reduce过程:把Map过程得出的结果进行分析汇总,输出R个输出文件作为最后结果.因此,在MapReduce编程模型下,对大规模的子任务进行调度是一个非常复杂的问题.由于每个任务都要分成Map过程中的M片,Reduce过程中的R片,而M与R要比worker的数量大很多,因此每个worker都要执行非常多的工作[13].
衡量调度任务策略优劣的目标主要有:服务质量QoS(Quality of Service)、最优跨度(Optimal Makespan)、负载均衡(Load Balancing)、经济原则(Economic Principle)等.其中,调度的跨度是最重要的指标,指云环境下从第一个任务开始算起,直到最后一个任务执行完毕所消耗的时间,跨度越短证明调度策略越好.考虑到云环境中每个虚拟机计算节点的计算能力不尽相同,以及每个任务对资源各项指数偏好也有差异,任务到虚拟机资源节点上的均衡分配以及服务质量也是衡量调度策略的重要因素,因此应将时间跨度和负载均衡结合作为评估目标的同时,充分考虑策略的服务质量,也就是任务与资源的匹配度.
本文依据云环境下模型的特点,提出一种适用于大规模并行处理系统的新的调度算法,即蚁群模拟退火算法,该算法充分利用蚁群算法解决大规模组合优化问题的并行性、正反馈性和鲁棒性的优势,并为避免蚁群算法易陷入局部最优解、收敛速度慢的缺点,利用模拟退火算法灵活、运行效率高和较少受到初始条件约束等优点,建立一个较优的分配调度策略. 并通过仿真实验可知,蚁群模拟退火算法进行任务调度可以在减少任务总完成时间的同时, 均衡系统负载,提高服务质量.
1.2 相关定义定义1 云环境下待执行的n个任务表示为T={T1, T2, ……Tn},m个虚拟机资源表示为集合V={V1, V2, ……Vm},用一个n×m的矩阵S表示任务在虚拟机资源上的执行时间矩阵,S ={Sij|Sij表示Ti在Vj上的执行时间,1 < i < n, 1 < j < m}. E是一个n×m的资源分配矩阵,E ={Eij|Eij表示Ti是否分配到Vj上执行,分配执行则Eij=1, 否则Eij=0,1 < i < n, 1 < j < m}.每个任务用六元组来表示,即
| $ {T_i} = \left\langle {{\rm{TI}}{{\rm{D}}_i},{\rm{T}}{{\rm{C}}_i},{\rm{T}}{{\rm{B}}_i},{\rm{T}}{{\rm{R}}_i},{\rm{T}}{{\rm{F}}_i},{\rm{T}}{{\rm{P}}_i}} \right\rangle , $ | (1) |
其中,TIDi表示任务编号,TCi表示任务期待资源cpu处理能力,TBi表示任务期待带宽,TRi表示任务期待内存,TFi表示任务期待资源故障率,TPi表示是任务期待资源费用.同样的,每个节点用六元组表示如下:
| $ {V_i} = \left\langle {{\rm{VI}}{{\rm{D}}_i},{\rm{V}}{{\rm{C}}_i},{\rm{V}}{{\rm{B}}_i},{\rm{V}}{{\rm{R}}_i},{\rm{V}}{{\rm{F}}_i},{\rm{V}}{{\rm{P}}_i}} \right\rangle , $ | (2) |
VIDi表示节点编号,VCi表示节点cpu处理能力,VBi表示节点带宽,VRi表示节点内存大小,VFi表示节点故障率,VPi表示节点使用价格.
定义2 根据用户不同需求来计算各个任务到每个资源节点的匹配程度,引入匹配因子,用户任务i与第j个资源节点匹配因子表示如下.
| $ {\rm{Matc}}{{\rm{h}}_{ij}} = 1/\sqrt {\sum\limits_{i = 1}^5 {{{\left( {{\rm{T}}{{\rm{m}}_i} - {\rm{V}}{{\rm{m}}_j}} \right)}^2}} } , $ | (3) |
其中,Tmi表示任务i对资源的期望值(由式(1)可得),Vmj表示第j个资源节点的参数权值(由式(2)可得).匹配因子越大,表明任务选择该资源节点能获得较好的资源服务质量.
定义3 设X是一个任务与资源的映射序列,则负载均衡度定义为
| $ {\rm{Load}}\left( X \right) = \sqrt {\sum\limits_{i = 1}^n {{{\left( {1 - {C_1}\frac{{{Y_i}}}{{{\rm{L}}{{\rm{v}}_i}}}} \right)}^2}} } , $ | (4) |
其中,Yi表示资源节点i上的任务量,Lvi表示资源节点的计算能力,C1为归一化参数,使得
| $ \begin{array}{l} {\rm{L}}{{\rm{v}}_i} = {W_1} \times n\left( {{V_i}} \right) + {W_2} \times p\left( {{V_i}} \right) + {W_3} \times b\left( {{V_i}} \right) + \\ {W_4} \times r\left( {{V_i}} \right). \end{array} $ | (5) |
定义4 云环境下任务调度的目标是对用户提交的任务实现最优调度,同时增强资源的负载均衡度.将时间跨度和负载均衡度综合作为衡量指标,则目标函数定义为
| $ F\left( X \right) = {\rm{Load}}\left( X \right) \times {\rm{Makespan}}\left( X \right), $ | (6) |
| $ {\rm{Makespan}}\left( X \right) = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{S_{ij}}} } \times {E_{ij}}, $ | (7) |
其中,Makespan(X)表示任务时间跨度.
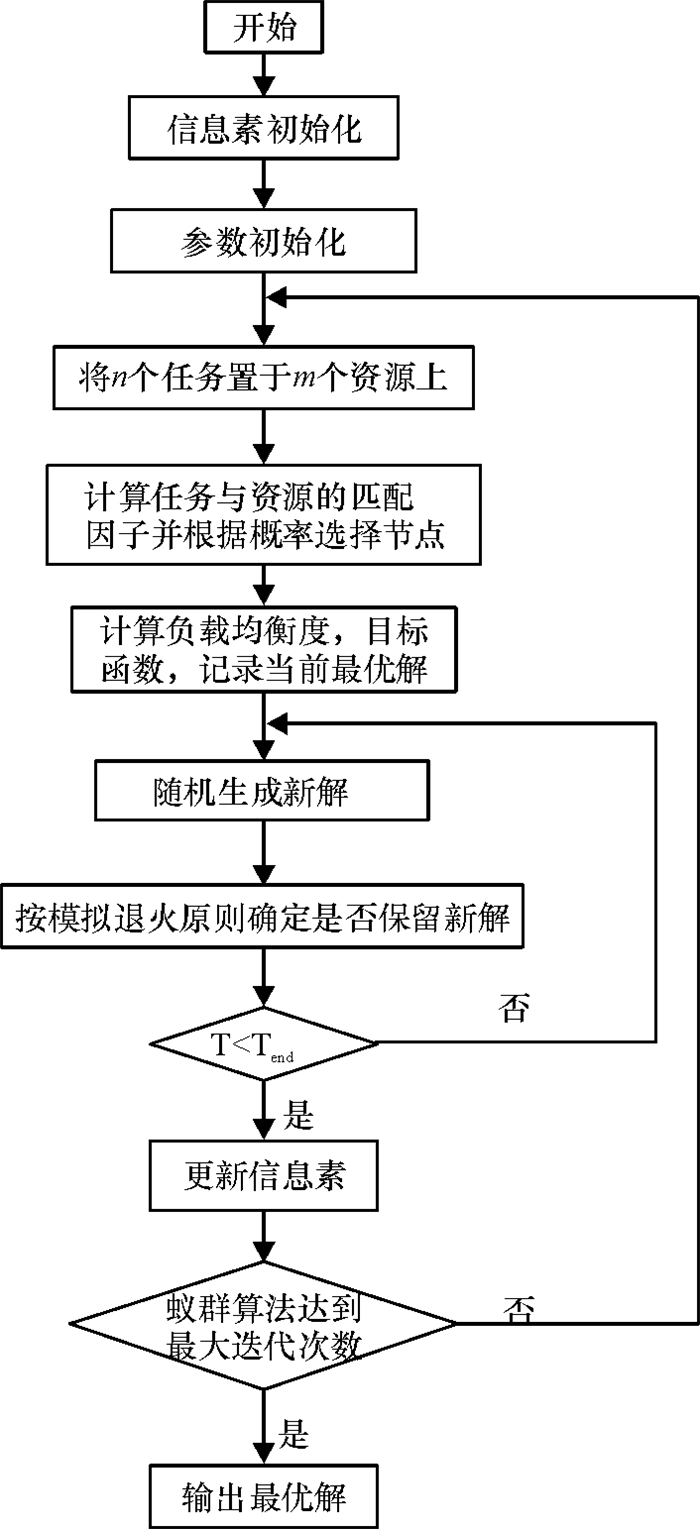
2 蚁群模拟退火算法蚁群模拟退火算法的基本思想是把模拟退火算法融入蚁群算法的路径优化和信息素更新中,从而使求解效率和服务质量更加理想.算法流程如图 2所示.
|
图 2 蚁群模拟退火算法流程图 Figure 2 Flow chart of ant colony simulated annealing algorithm |
(1) 信息素初始化.考虑到资源的可用性,若资源可用,则可设flagj=1;若资源退出或失效,则设flagj=0.文献[14]用节点的硬件资源来初始化一个节点的信息素.主要用cpu个数m,处理能力p,内存容量h,带宽b,故障率f来初始化信息素.并按式(8)为各参数设置阈值,若超过该阈值,则统一以阈值计算.
| $ {m_{\max }} = {m_0},{p_{\max }} = {p_0},{r_{\max }} = {r_0},{b_{\max }} = {b_0},{f_{\max }} = {f_0}. $ | (8) |
cpu的初始信息素为
| $ {\tau _{ip}}\left( 0 \right) = \frac{{m \times p}}{{{m_0}{p_0}}} \times 100\% . $ | (9) |
内存的初始信息素为
| $ {\tau _{ir}}\left( 0 \right) = \frac{r}{{{r_0}}} \times 100\% . $ | (10) |
带宽的初始信息素为
| $ {\tau _{ib}}\left( 0 \right) = \frac{b}{{{b_0}}} \times 100\% . $ | (11) |
故障率的初始信息素为
| $ {\tau _{if}}\left( 0 \right) = \frac{f}{{{f_0}}} \times 100\% . $ | (12) |
所有flagj=1的资源j的初始信息素[15-16] τ(t0)为
| $ \tau \left( {{t_0}} \right) = a{\tau _{ip}}\left( 0 \right) + b{\tau _{ir}}\left( 0 \right) + c{\tau _{ib}}\left( 0 \right) + d{\tau _{if}}\left( 0 \right), $ | (13) |
其中a+b+c+d=1.
(2) 根据式(6)得定义目标函数,初始化参数.
(3) 蚂蚁开始循环,将n个任务置于m个资源上.
(4) 计算任务到资源匹配因子Matchij作为启发信息,按式(14)计算转移概率,决定选择节点
| $ p = \frac{{{{\left[ {{\tau _{ij}}\left( t \right)} \right]}^\alpha }{{\left[ {{\rm{Matc}}{{\rm{h}}_{ij}}\left( t \right)} \right]}^\beta }}}{{\sum\limits_{k \in valid} {{{\left[ {{\tau _{ij}}\left( t \right)} \right]}^\alpha }{{\left[ {{\rm{Matc}}{{\rm{h}}_{ij}}\left( t \right)} \right]}^\beta }} }}, $ | (14) |
其中,τij(t)表示t时刻资源j上的信息素浓度,Matchij(t)表示t时刻任务i与资源j的匹配因子,α和β分别表示信息素浓度和匹配因子的重要程度.
(5) 计算负载均衡度和目标函数值,记录下蚁群此代最优解X.
(6) 运用模拟退火算法优化路径与更新信息素.
传统的蚁群算法(ACO)算法对每代蚂蚁遍历的序列不进行任何的处理,一直循环到最终收敛或者达到最大蚂蚁代数,退出循环并返回算法结果,降低了搜索性能.在这里引入了Boltzmann机制优化路径和更新信息素,具体算法如下:
Step1 对蚁群算法第i次迭代生成的最优解X随机交换两资源节点的任务形成新解X'.
Step2 以模拟退火的原则保留X还是X',计算目标函数大小F(X)和F(X'),若ΔF=F(X')-F(X) < 0, 则,用X'替代X;否则若exp(-ΔF/T) > rand(0, 1),则也用X'代替X,否则,就保留X抛弃X'.退火温度按照T(t+1)= λT(t)进行迭代.其中T为退火温度,初始化温度为T0, 终止温度为Tend, λ为退火系数.
Step3 若T < Tend模拟退火继续迭代,否则结束.
Step4 对模拟退火算法得出的最优解进行信息素的更新,释放信息素公式为
| $ \Delta \tau _{ij}^k\left( {t + 1} \right) = \left( {1 - \rho } \right)\tau _{ij}^k\left( t \right) + \sum\limits_{k = 1}^m {\Delta \tau _{ij}^k} , $ | (15) |
其中,ρ为信息素挥发系数,Δτijk为每次迭代结束后最优解在路径(i, j)上释放的信息素.
(7) 循环执行达到最大蚂蚁迭代次数,退出循环并返回算法结果,否则执行(3).
3 算法分析和仿真实验为验证新算法,采用扩展Cloudsim云计算仿真平台[17]做模拟.并将本文提出的任务调度策略与基于基本蚁群系统ACO的任务调度策略在调度时间方面进行比较.
3.1 试验参数设置算法中的a,b,c,d分别表示资源节点的cpu计算能力,内存,带宽,故障率的重要性,由于任务的执行受处理器处理能力的影响较大,因此把a,b,c,d的值分别设为0.4,0.2,0.2,0.2.由于信息素挥发系数过大易使解陷入局部最优解,过小会导致算法收敛速度过慢,于是本文综合考虑算法全局搜索能力和收敛速度两项指标,选择信息素挥发系数为0.5.α,β,分别表示信息素,匹配因子的重要性,y表示产生多少蚂蚁效果更好,退火系数λ决定退火的快慢.通过实验来获得α,β,y,λ的最优组合.虚拟机节点设为200个,Master的定时器设为5 s.任务大小为200 M,虚拟机处理能力为100~400 MIPS,内存容量为512 M~2 G,带宽为1~4 M/s,故障率为10%~30%.T0设为105,Tend设为104.
3.2 实验结果及分析首先提交一个任务大小为2 000 M的作业,该作业重复提交12次,最后得出有6次当α=1,β=2,y=4,λ=0.95时,为作业任务调度有效节点的时间最少.然后用不同作业大小的作业重复上述过程,最后得出50%的作业当α=1,β=2,y=4,λ=0.95为最优组合.表 1给出了作业大小为2000 M,α,β,y,λ取不同值时,任务调度的时间变化.因此取α=1,β=2,y=4,λ=0.95.
| 表 1 参数设置表 Table 1 Parameter table |
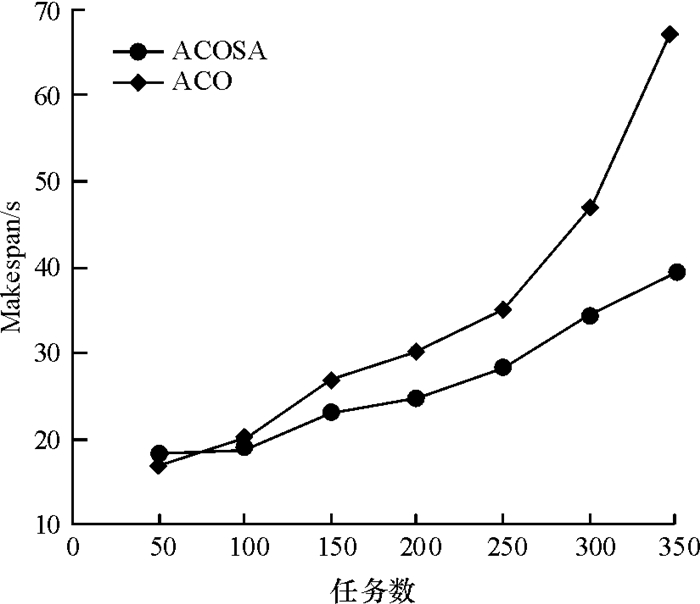
图 3为基于模拟退火蚁群算法(ACOSA)任务调度和基于基本蚁群算法(ACO)任务调度时间图.两种算法均调度350个任务,每增加50个任务进行一次数据采样.
|
图 3 任务调度时间图 Figure 3 Task scheduling time |
从图 3可以看出,当任务量较少时,ACOSA和ACO的区别不大,ACO略占优势;但当任务量逐渐增大时,ACO花费的时间呈剧增状态,而ACOSA只是平缓增大.
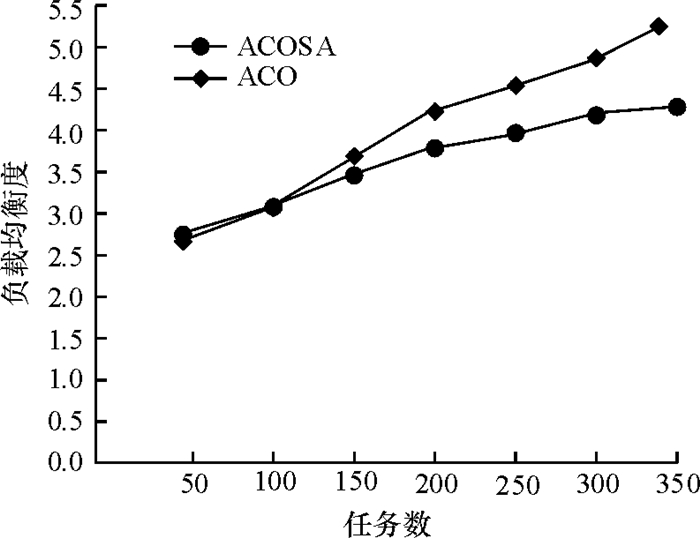
图 4为两个算法的系统均衡度对比图.由图 4可看出虽然ACOSA算法在任务量较少时负载均衡性能比ACO算法优势不大,但随着任务量的增加,ACOSA算法的负载均衡性能要明显优于ACO算法.
|
图 4 系统负载均衡度 Figure 4 Load balance degree of the system |
因此在云环境下采用ACOSA算法进行任务调度更符合云计算的大规模运算的需求.这主要是因为相比ACO,ACOSA算法蚂蚁走下一步时使用匹配因子使得在任务选择资源节点时可以选择处理能力较强的资源,在任务跨度计算式加入负载均衡因子使得资源整体负载趋于均衡,这都能使得当处理海量任务时调度时间有效减小.为了使蚁群算法得出的最优解是全局最优解,在蚁群算法后期引入退火算法,有效增强了算法的全局搜索能力,避免了蚁群算法的缺陷.
4 结束语为了克服蚁群算法在大规模的云环境下任务的调度出现速度慢、易陷入局部最优解的缺点,提出基于蚁群模拟退火算法(ACOSA)的任务调度策略,该算法从调度完成时间、负载均衡、任务与节点的匹配度,以及优化全局最优解来进行调度的优化,使用户任务更迅速找到合适的虚拟机资源并分配任务.实验证明改进的算法比基于基本蚁群算法(ACO)的任务调度在调度时间和负载均衡方面有更好的表现.云计算环境下的任务调度目标还涉及其他方面,如经济原则,这将是今后的研究方向.
| [1] |
Jadeja Y, Modi K. Cloud computing-concepts, architecture and challenges[C]//Proceedings of the International Conference on Computing, Electronics and Electrical Technologies. India: IEEE, 2012: 877-880.
|
| [2] |
Mollah M B, Islam K R, Islam S S. Next generation of computing through cloud computing technology[C]//Proceedings of the IEEE Canadian Conference on Electrical and Computer Engineering. Montreal QC: IEEE, 2012: 67-72.
|
| [3] |
Islam S S, Mollah M B, Huq M I, et al. Cloud computing for future generation of computing technology[C]// Proceedings of the IEEE International Conference on Cyber Technology in Automation, Control and Intelligent Systems. Bangkok: IEEE, 2012: 129-134.
|
| [4] |
师凯, 蔡延光, 邹谷山, 等. 分段蚁群算法在运输调度问题中的应用[J].
广东工业大学学报, 2006, 23(1): 71-76.
Shi K, Cai Y G, Zou G S, et al. Application of subsection ant colony algorithm to vehicle routing problems[J]. Journal of Guangdong University of Technology, 2006, 23(1): 71-76. |
| [5] |
王银年, 葛洪伟. 求解TSP问题的改进模拟退火遗传算法[J].
计算机工程与应用, 2010, 46(5): 44-47.
Wang Y N, Ge H W. Improved simulated annealing genetic algorithm for solving TSP problem[J]. Computer Engineering and Applications, 2010, 46(5): 44-47. |
| [6] |
李敬花. 遗传蚁群融合算法求解多项目资源能力平衡问题[J].
计算机集成制造系统, 2010, 16(3): 643-649.
Li J H. Combination of genetic & ant colony algorithms for multi-project resource leveling problem[J]. Computer Integrated Manufactu ring Systems, 2010, 16(3): 643-649. |
| [7] |
李凌宇, 郭贵法, 许锦标. 基于模拟退火遗传算法的PID参数整定与优化[J].
广东工业大学学报, 2010, 27(2): 80-83.
Li L Y, Guo G F, Xu J B. Optimizing and adjusting the parameter of PID based on simulated annealing genetic algorithms[J]. Journal of Guangdong University of Technology, 2010, 27(2): 80-83. |
| [8] |
华夏渝, 郑骏, 胡文心. 基于云计算环境的蚁群优化计算资源分配算法[J].
华东师范大学学报, 2010(1): 112-117.
Hua X Y, Zheng J, Hu W X. Ant colony optimization algorithm for computing resource allocation based on cloud computing environment[J]. Journal of East China Normal University, 2010(1): 112-117. |
| [9] |
范杰, 彭舰, 黎红友. 基于蚁群算法的云计算需求弹性算法[J].
计算机应用, 2011, 31(S1): 1-7.
Fan J, Peng J, Li H Y. Demand elasticity algorithm for cloud computing based on ant colony optimization algorithm[J]. Journal of Computer Applications, 2011, 31(S1): 1-7. |
| [10] |
王静宇, 谭跃生, 陈振江. 基于遗传蚁群混合算法的网格任务调度研究[J].
计算机与信息技术, 2010(6): 53-55.
Wang J Y, Tan Y S, Chen Z J. Research on grid task scheduling based on genetic algorithm ant colony algorithm[J]. Computer and information technology, 2010(6): 53-55. |
| [11] |
吕良干. 云计算环境下资源负载均衡调度算法研究[D]. 乌鲁木齐: 新疆大学信息科学与工程学院, 2010: 114-119.
|
| [12] |
Li K, Xu G C, Zhao G Y, et al. Cloud task scheduling based on load balancing ant colony optimization[C]//Proceedings of the Sixth Annual ChinaGrid Conference. Liaoning: IEEE, 2011: 266-270.
|
| [13] |
李建峰, 彭舰. 云计算环境下基于改进遗传算法的任务调度算法[J].
计算机应用, 2011, 31(1): 184-186.
Li J F, Peng J. Task scheduling algorithm based on improved genetic algorithm in cloud computing environment[J]. Journal of Computer Applications, 2011, 31(1): 184-186. |
| [14] |
张千, 梁鸿, 李振. 基于改进蚂蚁算法的网格资源管理的研究[J].
微电子学与计算机, 2009, 26(9): 71-74.
Zhang Q, Liang H, Li Z. Research of grid resource management system based on improved ant algorithm[J]. Microelectronics and Computer, 2009, 26(9): 71-74. |
| [15] |
魏东, 吴良杰, 佐丹, 等. 基于混合蚁群算法的网格任务调度[J].
计算机工程, 2010, 36(3): 215-217.
Wei D, Wu L J, Zuo D, et al. Grid task schedule based on hybrid ant colony algorithm[J]. Computer Engineering, 2010, 36(3): 215-217. |
| [16] |
寇晓丽, 刘三阳, 郑巍. 一种基于模块度分簇的改进蚁群算法求解大规模TSP问题[J].
电子学报, 2009, 33(5): 125-130.
Kou X L, Liu S Y, Zheng W. An improved ant colony algorithm based on modularity clustering for solving the large scale TSP problems[J]. Chinese Journal of Electronics, 2009, 33(5): 125-130. |
| [17] |
Zhao W, Peng Y, Xie F, et al. Modeling and simulation of cloud computing: a review[C]//Proceedings of the IEEE Asia Pacific Cloud Computing Congress. Shenzhen: IEEE, 2012: 20-24.
|
 2014, Vol. 31
2014, Vol. 31