2. 中国地质大学 数学与物理学院,湖北 武汉 430074
2. School of Mathematics and Physics, China University of Geosciences, Wuhan 430074, China
随着互联网和信息技术的不断发展,人们逐渐由信息匮乏时期过渡到信息过载时代.在这个时代,对信息消费者,从大数据集中找到有用的信息难度逐渐增大;而对于信息产生者,则难以让自己的信息从大数据集中被更多人关注.很多大型的电子商务网站为了解决这一问题,在系统中引入了推荐系统,来帮助用户更高效、更准确地找到有用的信息.其中,应用最多的是协同过滤推荐算法[1].
根据过滤操作对象来划分,协同过滤算法可以分为基于用户的协同过滤(UBCF)算法和基于项目的协同过滤(IBCF)算法[2].UBCF算法先找到和目标用户有相似兴趣的用户集合,然后在这个用户集合中找到相似用户喜欢的,而目标用户没有评价过的项目推荐给目标用户.IBCF算法先计算项目之间的相似度,然后再结合项目的相似度与目标用户的历史行为给目标用户推荐项目.
在实际应用中,数据量的不断增加使得数据稀疏性的问题在基于大数据集的用户-项目评分矩阵中表现得越来越严重.数据的稀疏性会使得项目之间的重叠性降低,由此计算出来的相似度准确率不高,推荐质量也会严重下降.针对这些问题,研究者们提出了很多解决方法:基于项目评分预测与填充[3]、聚类[4]、核[5]、奇异矩阵分解[6]、神经网络[7]、贝叶斯[8]、相似度传播[9]和信任模型[10]等.这些方法在一定程度上克服了数据稀疏性给相似性计算带来的一些问题.但这些方法在计算相似性时都没有考虑不同类别项目间的相似性和用户兴趣漂移,并且在相似近邻的选取上存在一些弊端,这些都会导致推荐质量的下降.针对上述问题本文提出了一种混合动态协同过滤算法(Hybrid Dynamic Collaborative Filtering,简称HDCF).
1 传统协同过滤算法假定推荐系统中用户评分数据包含有m个用户和n个项目,分别表示为U={U1, U2, …Um}和I={I1, I2, …In}.用一个m×n阶矩阵表示用户对项目的评分记录,如表 1所示.表 1中的m行代表m个用户,n列代表n个项目,假设用户Ui对项目Ij(Ui∈U,Ij∈I)的评分为Ri, j, 这个分数体现了用户Ui对项目Ij的兴趣.
| 表 1 用户-项目评分矩阵R(m×n) Table 1 Users-item rating matrix R(m×n) |
相似性计算方法有很多,常用的主要有以下3种[11]:(1)余弦相似性度量方法(CSM);(2)修正的余弦相似性度量方法(ACSM);(3)皮尔逊相关(Pearson)相似性度量方法.
本文采用皮尔逊相关相似性度量方法来计算项目之间的相似性,假设U(i)∩U(j)表示对项目i与项目j有共同评分的用户集合,那么项目i与项目j的相似性sim(i, j)[3]可以由式(1)表示为
| $ \begin{array}{l} {\rm{sim}}\left( {i, j} \right) = \\ \frac{{\sum\limits_{u \in U\left( i \right) \cap U\left( j \right)} {\left( {{R_{u, i}}-\overline {{R_i}} } \right)\left( {{R_{u, j}}-\overline {{R_j}} } \right)} }}{{\sqrt {\sum\limits_{u \in U\left( i \right) \cap U\left( j \right)} {{{\left( {{R_{u, i}}-\overline {{R_i}} } \right)}^2}} } \sqrt {\sum\limits_{u \in U\left( i \right) \cap U\left( j \right)} {{{\left( {{R_{u, j}} - \overline {{R_j}} } \right)}^2}} } }}. \end{array} $ | (1) |
其中, 用户u对项目i和j的评分分别表示为Ru, i、Ru, j;项目i和项目j获得的平均评分分别表示为
计算出目标项目与其他项目的相似性后,将相似性最大的前K个项目作为相似近邻,然后计算目标用户对它们的预测评分,选择得分最高的N(N≥1)个项目推荐给目标用户,评分预测公式如下:
| $ {P_{u, i}} = \overline {{R_i}} + \frac{{\sum\limits_{j \in s\left( i \right)} {{\rm{sim}}\left( {i, j} \right) \times \left( {{R_{u, j}}-\overline {{R_j}} } \right)} }}{{\sum\limits_{j \in s\left( i \right)} {{\rm{sim}}\left( {i, j} \right)} }}. $ | (2) |
其中,项目i的最近邻项目用集合表示为s(i)={ii1, ii2, …, iik},(i∉s(i)); 目标项目i获得的平均评分表示为
传统协同过滤算法不太适应大数据集中数据非常稀疏的情况,并且在计算相似性时没有考虑项目分类问题.此外,在实际应用中用户对项目的评分及兴趣是随时间动态变化的,传统的相似性计算没有考虑时间因素.针对传统协同过滤算法的这些缺点,HDCF算法做了一些改进.
2.1 改进的相似性度量方法当大数据集中用户-项目评分矩阵数据极度稀疏时(如表 1所示),式(1)在实际应用中并不能取得理想的效果,因为这样计算出来的相似性具有一定的偶然性.文献[12]提出一种增加阈值τ的方法来调整相似性计算:
| $ {\rm{sim'}}\left( {i, j} \right) = \frac{{\min \left( {\left| {{U_i} \cap {U_j}} \right|, \tau } \right)}}{\tau } \times {\rm{sim}}\left( {i, j} \right), $ | (3) |
其中|Ui∩Uj|表示对项目i与项目j都有过评分的用户个数,min(|Ui∩Uj|, τ)表示取|Ui∩Uj|和τ中数值的最小值.
但式(3)也存在一定的弊端,如实际应用环境不断变化时,τ值的确定比较困难.针对式(3)中阈值设置的这种不足,本文在度量项目间相似性时利用了Jaccard系数并引入权重系数α来自适应地调节数据稀疏性对相似性的大小的影响.对式(1)改进如下:
| $ {\rm{sim}}_r^*\left( {i, j} \right) = \left( {1-\alpha } \right) + \alpha \frac{{\left| {{U_i} \cap {U_j}} \right|}}{{\left| {{U_i} \cup {U_j}} \right|}}{\rm{sim}}\left( {i, j} \right). $ | (4) |
其中|Ui∪Uj|表示给项目i与项目j评过分的用户总数;α为权重系数,且α∈(0, 1],加入权重系数α后不同的推荐系统可以根据实际情况动态调整相似性的增长快慢.从式(4)可以看出对两个项目有共同评分的用户数越多,则项目间的相似性越大,反之项目间的相似性就越小.
2.2 项目类别相似性式(1)计算出来的相似性往往倾向于使两个不同领域的热门项目之间具有较高的相似性.例如某些人特别喜欢看新闻联播,不看其他新闻.而有些人则特别喜欢看电视剧,如果按照上述公式计算,黄金时段的电视剧和新闻联播具有较高的相似性,而新闻联播和其他新闻相似度却很低.这显然是不合理的.新闻联播和黄金时段电视剧分别属于不同的项目类别,本文在计算项目间的相似性时考虑引入项目类别相似性.
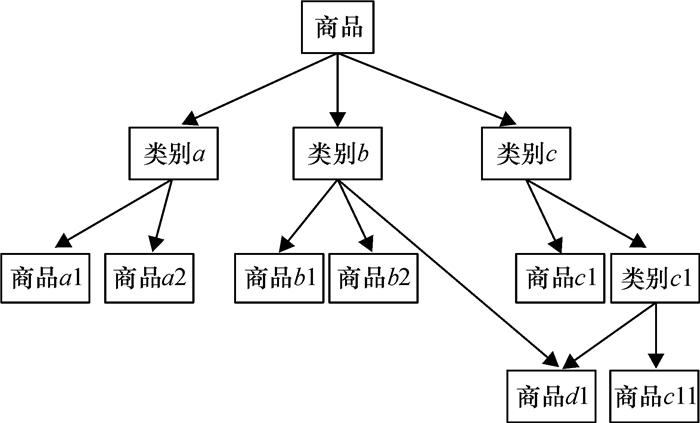
在实际应用中,项目一般都是按类别划分为若干子类,每个子类又被分成若干更小的子类,如图 1所示.
|
图 1 商品分类树 Figure 1 Product category tree |
从图 1可以看出,处于同一类别的项目,因为它们在内容上具有更多共同之处,应该具有更大的相似性.例如在不考虑评分的情况下,商品a1和商品a2的相似性应该高于商品a1和商品b1的相似性,即simc(a1, a2)>simc(a1, b1).为了具体量化这种差异,本文采用一种语义相似性计算公式[13]:
| $ {\rm{si}}{{\rm{m}}_c}\left( {i, j} \right) = \frac{{2{\rm{depth}}\left( {{\rm{LCA}}\left( {{l_i}, {l_j}} \right)} \right)}}{{{\rm{depth}}\left( {{l_i}} \right) + {\rm{depth}}\left( {{l_j}} \right)}}, $ | (5) |
其中,LCA(li, lj)表示节点i和节点j具有最大公共路径的节点数,depth(li)表示节点i的层次,本文定义根节点的层次值为0,根节点的子节点层次值为1,依次类推.从式(5)可以看出对于项目i和项目j同属的相同类别越多,它们的相似性越大.
2.3 用户的兴趣和评分的动态性传统算法在计算相似性时,没有考虑用户评分和兴趣随时间变化的情况.一般来说用户在相隔较短的时间内喜欢的项目更能够体现其当前的兴趣,因此在给用户推荐项目时,应该加大对用户近期行为的权重.数学中有许多衰减函数,这里笔者选择其中一个并给自变量引入系数β,自变量为用户对两个项目产生行为的时间差的绝对值,具体如式(6)所示:
| $ f\left( {\left| {{t_{ui}}-{t_{uj}}} \right|} \right) = \frac{1}{{1 + \beta \left| {{t_{ui}}-{t_{uj}}} \right|}}, $ | (6) |
其中tui是用户u对项目i产生行为的时间,tuj是用户u对项目j产生行为的时间.β是时间权值,可以根据不同的系统动态调节.例如当一个系统中用户兴趣变化很快时,β可以设置为较大的值,反之β可以设置为较小的值.函数f的含义是:用户对项目i和项目j产生行为的时间间隔越大,则f(|tui-tuj|)取的值越小.因此,引入时间衰减函数之后项目间的相似性simr(i, j)为
| $ {\rm{si}}{{\rm{m}}_r}\left( {i, j} \right) = f\left( {\left| {{t_{ui}}-{t_{uj}}} \right|} \right) \times {\rm{sim}}_r^*\left( {i, j} \right). $ | (7) |
定义项目的综合相似性sims(i, j)计算方法如式(8)所示.
| $ {\rm{si}}{{\rm{m}}_s}\left( {i, j} \right) = \left( {1-\lambda } \right){\rm{si}}{{\rm{m}}_r}\left( {i, j} \right) + \lambda {\rm{si}}{{\rm{m}}_c}\left( {i, j} \right), $ | (8) |
其中λ为权重系数,且满足λ ∈[0, 1].对λ的取值问题,通常的做法是在[0, 1]中取一系列值观察不同的λ对预测结果的影响,然后从中选择较理想的值[14].然而这种方法在理论研究中尚可,但是在实际应用中条件是经常变化的,因此这种方法并不可取.
针对上述问题,HDCF算法采用了一种自适应权重系数模型,可以根据simr(i, j)和simc(i, j)的值来动态地调节λ值的大小.具体表达式如下:
| $ \lambda = \frac{{{\rm{sim}}_c^2\left( {i, j} \right)}}{{{\rm{sim}}_r^2\left( {i, j} \right) + {\rm{sim}}_c^2\left( {i, j} \right)}}. $ | (9) |
从式(9)可以看出,当simc(i, j)为0时,λ的值为0,sims(i, j)的值完全由simr(i, j)来决定;同理,当simr(i, j)为0时,sims(i, j)的值完全由simc(i, j)确定.这样,当项目类别具有较高的相似性时,在计算综合相似性时就可以获得较大的权重,符合实际需求,因此也说明式(9)中λ取值的合理性.
2.5 项目近邻的选取对于项目近邻的选取,一般的方法是选择相似性最大的前K个项目[15].大数据集数据的稀疏性使得不同项目的相似项目的数量差距可能很大,有的项目的相似项目数量可能远大于K个,而有些项目的相似项目的数量可能不足K个.针对这种情况,汪静等[16]引入了相似性阈值θ,只有当相似性大于θ时,才会被选作近邻项目.由于数据的稀疏性会使得相似性计算具有一定的偶然因素,而且θ的值难以确定.杨兴耀等[17]采用相似对象数目百分数Percentage作为对象邻居的选取标准.但是对于大数据集中项目的相似性项目数量很大时,引入Percentage后近邻项目数可能依然会比较多,这样在计算预测评分时会增加时间复杂度.
为此,本文提出一种改进的项目近邻选取办法,既不会增加计算的时间复杂度,又能够较好地适应相似项目数量不高的情况.用Is表示目标项目i与其他项目相似度集合,且Is={ji1, ji2, …, jik},i∉Is.Is中的相似性降序排列. |Is|表示相似项目的个数.项目i的最近邻项目集合s(i)可表示为
| $ s\left( i \right) = \left\{ \begin{array}{l} \left\{ {{j_{i1}}, {j_{i2}}, \cdots, {j_{iK}}} \right\}, \left( {\left| {{I_s}} \right| \ge K} \right), \\ \left\{ {{j_{i1}}, {j_{i2}}, \cdots, {j_{i{\rm{per}}\left| {{I_s}} \right|}}} \right\}, \left( {\left| {{I_s}} \right| < K} \right). \end{array} \right. $ | (10) |
其中per |Is|表示百分数Percentage与|Is|的乘积.当|Is|的值大于等于K时, s(i)取Is的前K个作为项目近邻,当|Is|的值不足K个时, 就取Is的前Percentage个作为项目近邻.这样既可以克服数据稀疏时项目相似性带来的影响,又不会增加计算的时间复杂度.
最后产生评分预测公式为
| $ {P_{u, i}} = \overline {{R_i}} + \frac{{\sum\limits_{j \in s\left( i \right)} {{\rm{si}}{{\rm{m}}_s}\left( {i, j} \right) \times \left( {{R_{u, j}}-\overline {{R_j}} } \right)} }}{{\sum\limits_{j \in s\left( i \right)} {{\rm{si}}{{\rm{m}}_s}\left( {i, j} \right)} }}. $ | (11) |
输入:目标用户ui,用户-项目评分矩阵R (m×n),项目分类矩阵G (a×b),权重指数α,时间衰减参数β,最近邻居个数K以及百分数Percentage.
输出:给目标用户推荐的top-N项目集合
(1) 在用户-项目评分矩阵R (m×n)中选取任意项目i、j(i≠j).根据式(1)计算出i与j的相似性sim(i, j).
(2) 分别计算给项目i和项目j评过分的用户数集合C(Ui)和C(Uj).根据C(Ui)和C(Uj)计算出项目i与项目j共同评分的用户个数|Ui∩Uj|和给项目i与项目j评过分的用户总数|Ui∪Uj|,根据式(4)计算项目相似性simr*(i, j).
(3) 根据项目i和项目j的的时间属性,利用公式(7)计算项目i与项目j的相似性simr(i, j).
(4) 根据用户-项目评分矩阵R (m×n)和项目分类矩阵G (a×b)利用式(5)计算项目i和项目j的类别相似性simc(i, j).
(5) 利用simr(i, j)和simc(i, j)计算出相似性权重系数λ,将λ、simr(i, j)、simc(i, j)代入式(8)计算出项目的综合相似性sims(i, j).
(6) 重复步骤(1)~(5),计算出项目i的相似项目集合Is.
(7) 将K、Percentage、Is代入式(10)计算邻居项目集合s(i).
(8) 由sims(i, j)和邻居项目集合s(i)根据式(11)计算出用户ui对项目i的预测评分Pu, i.推荐结果为预测评分最高的前N个项目.
4 实验结果及分析 4.1 数据集实验数据采用的是目前被广泛使用的由美国明尼苏达大学提供的Movielens数据集.该数据集中有1 682部电影,所有电影分别属于19种电影类别,943个用户对电影进行了评分.评分时间跨度是8个月,评分纪录总数有10万多条.用户和项目的评分矩阵密度为
| $ \frac{{100\;000}}{{943 \times 1\;682}} = 6.3\% . $ |
由此可以看出此数据集非常稀疏.随机抽取数据集的80%条记录作为训练集,剩余的作为测试集.
4.2 度量标准由于平均绝对偏差(Mean Absolute Error, MAE)具有直观、便于理解等特点,因此实验采用MAE作为度量标准,MAE计算的是项目的预测评分与项目的实际评分之间的平均绝对偏差[15].
| $ {\rm{MAE = }}\frac{{\sum\limits_{i = 1}^N {\left| {{p_i}-{q_i}} \right|} }}{N}, $ |
其中, N代表预测项目数量,pi是用户对第i个项目的预期评分,qi是用户对第i项目的实际评分. MAE越小,则说明预测评分与实际评分越接近,推荐算法的质量越高.
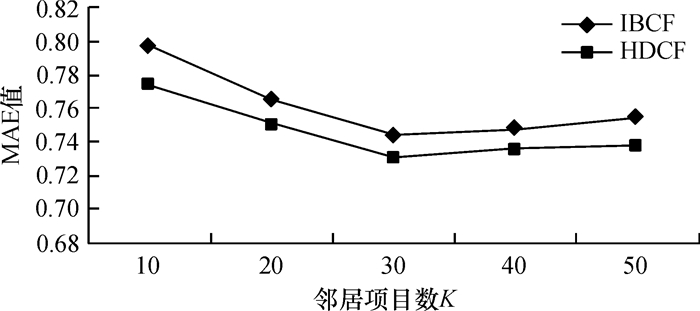
4.3 HDCF算法与其他协同过滤算法的比较为了验证本文提出的HDCF算法的有效性,实验中将HDCF算法与IBCF算法的MAE值进行了比较,Percentage=0.65[17],权重系数α=β=0.65, 邻居近邻数K从10个开始逐步递增,结果如图 2所示.
|
图 2 MAE值比较 Figure 2 Comparison of MAE value |
从图 2可以看出,HDFC算法较IBCF算法具有较小的MAE值,且邻居项目数由10增加到30时MAE值逐渐减小,邻居值在30以后变化时,MAE值逐渐趋于稳定.由此可知HDCF算法相对于IBCF算法,推荐质量有所提高.因为HDFC算法将项目的类别信息加入到项目相似度计算当中,HDFC算法在计算相似性时还考虑了用户兴趣的时变性,这样距离用户产生行为时间越近的项目相似性越大,反之越小;HDFC算法在项目近邻的选取和相似性度量方法上更具有合理性.
5 结论针对传统推荐算法没有考虑项目类别、用户兴趣和评分动态性、近邻项目选取方法的不合理等问题,本文提出了一种基于大数据集的混合动态协同过滤算法,在计算项目的相似性时引入了时间衰减函数,考虑了分类后项目的相似性.此外,HDCF算法还对相似近邻数目的选取方法做了一些改进.实验结果表明该算法对推荐质量有一定的改善.
下一步的工作是针对实际应用中,电子商务站点项目数量庞大,计算项目间相似性时间过长的问题,将HDCF算法与Hadoop结合,实现分布式计算,以提高相似性的计算速度.
| [1] |
黄创光, 印鉴, 汪静, 等. 不确定近邻的协同过滤推荐算法[J].
计算机学报, 2010, 33(8): 1370-1377.
Huang C G, Yin J, Wang J, et al. Uncertain neighbors, collaborative filtering recommendation algorithm[J]. Chinese Joumal of Computers, 2010, 33(8): 1370-1377. |
| [2] |
孙光福, 吴乐, 刘淇, 等. 基于时序行为的协同过滤推荐算法[J].
软件学报, 2013, 24(11): 2721-2733.
Sun G F, Wu L, Liu Q, et al. Recommendations based on collaborative filtering by exploiting sequential behaviors[J]. Journal of Software, 2013, 24(11): 2721-2733. |
| [3] |
邓爱林, 朱扬勇, 施伯乐. 基于项目评分预测的协同过滤推荐算法[J].
软件学报, 2003, 14(9): 1621-1628.
Deng A L, Zhu Y Y, Shi B L. A collaborative filtering recommendation algorithm based ontem rating prediction[J]. Jorunal of Software, 2003, 14(9): 1621-1628. |
| [4] |
Gong S J, Ye H W. Joining useer clusteri-ng and item based collaborative filtering in personaliz-ed recommendtion serviced[C]//Proc of International of International Conference of Industrial and Information Systems. Washington DC: IEEE Computer Sciety, 2009: 149-151.
|
| [5] |
王鹏, 王晶晶, 俞能海. 基于核方法的User-Based协同过滤推荐算法[J].
计算机研究与发展, 2013, 50(7): 1444-1451.
Wang P, Wang J J, Yu N H. A kernel and user-based collaborative filtering recommendation algorithm[J]. Journal of Computer Research and Develop-ment, 2013, 50(7): 1444-1451. DOI: 10.7544/issn1000-1239.2013.20111660. |
| [6] |
杨兴耀, 于炯, 吐尔根·依布拉音, 等. 融合奇异和扩散过程的协同过滤模型[J].
软件学报, 2013, 24(8): 1868-1884.
Yang X Y, Yu J, Ibrahim T, et al. Collaborative fil-tering model fusing singularity and diffusion process[J]. Journal of Software, 2013, 24(8): 1868-1884. |
| [7] |
张锋, 常会友. 使用BP神经网络缓解协同过滤推荐算法的稀疏性问题[J].
计算机研究与发展, 2006, 43(4): 667-672.
Zhang F, Chang H Y. Employing BPnewalnetworks to alleviate the sparsity issue in collaborative filtering recommendation algorithms[J]. Journal of Computer Research and Development, 2006, 43(4): 667-672. |
| [8] |
李大学, 谢明亮, 赵学斌. 基于朴素贝叶斯方法的协同过滤推荐算法[J].
计算机应用, 2010, 30(6): 1523-1526.
Li D X, Xie M L, Zhao X B. Collaborative filtering recomm endation algorithm based on maive Bayesian method[J]. Journal of Computer Applications, 2010, 30(6): 1523-1526. |
| [9] |
赵琴琴, 鲁凯, 王斌. SPCF:一种基于内存的传播式协同过滤推荐算法[J].
计算机学报, 2013, 36(3): 671-676.
Zhao Q Q, Lu K, Wang B. SPCF:A menmry based collaborative filtering algorithm via propagetion[J]. Chinese Journal of Computer, 2013, 36(3): 671-676. |
| [10] |
贾冬艳, 张付志. 基于双重邻居选取策略的协同过滤推荐算法[J].
计算机研究与发展, 2013, 50(5): 1076-1084.
Jia D Y, Zhang F Z. A collaborative filtering recommendation algorithm based on double neighborchoosing strategy[J]. Journal of Computer Research and Development, 2013, 50(5): 1076-1084. DOI: 10.7544/issn1000-1239.2013.20110896. |
| [11] |
张光卫, 李德毅, 李鹏, 等. 基于云模型的协同过滤推荐算法[J].
软件学报, 2007, 18(10): 2403-2411.
Zhang G W, Li D Y, Li P, et al. A collaborative filtering recommendation algorithm based in cloud model[J]. Journal of Software, 2007, 18(10): 2403-2411. |
| [12] |
Ma H, King I, Lyu M R. Effdctive missing data prediction for collaborative filter[C]//Proceedings of the 30th Annual International ACM SIGIR Conference. Netherlands Amsterdam: [s. n], 2007: 39-46.
|
| [13] |
Ganesan P, Garcia-Molina H. Exploiting hierchical d-omain sructure to computer similarity[J].
ACM Transact-ions on Information Systems, 2003, 21(1): 64-93.
DOI: 10.1145/635484. |
| [14] |
王茜, 王均波. 一种改进的协同过滤推荐算法[J].
计算机科学, 2010, 37(6): 226-234.
Wang Q, Wang J B. Improved collaborative filtering recommendation algorithm[J]. Computer Science, 2010, 37(6): 226-234. |
| [15] |
韦素云, 业宁, 朱健, 等. 基于项目聚类的全局最近邻的协同过滤算法[J].
计算机科学, 2012, 39(12): 149-152.
Wei S Y, Ye N, Zhu J, et al. Collaborative filtering re-commendation algorithm based on item clustering and global similarity[J]. Computer Science, 2012, 39(12): 149-152. DOI: 10.3969/j.issn.1002-137X.2012.12.034. |
| [16] |
汪静, 印鉴. 一种优化的Item-based协同过滤推荐算法[J].
小型微型计算机系统, 2010, 12(31): 2337-2342.
Wang J, Yin J. Optimized item-based collaborative filtering recommendation algorithm[J]. Joumal of Chinese Computer Systems, 2010, 12(31): 2337-2342. |
| [17] |
杨兴耀, 于炯, 吐尔根·依布拉音, 等. 综合用户和项目预测的协同过滤模型[J].
计算机应用, 2013, 33(12): 3354-3358.
Yang X Y, Yu J, Ibrahim T, et al. Collaborative filtering model combining users and items predictions[J]. Journal of Computer Applications, 2013, 33(12): 3354-3358. |
 2014, Vol. 31
2014, Vol. 31