近年来,随着移动互联网的普及以及电子商务等互联网应用的崛起,数据挖掘在这些行业的应用越发得到重视[1-2].要得到好的数据挖掘结果,必须要有高质量的数据集,但现实环境下收集到的数据往往不完整、不一致,因此,在数据挖掘应用中,噪声点的预处理很重要[3-10].
传统的噪声点预处理算法DBSCAN是一种基于密度的空间聚类算法.该算法利用基于密度的聚类概念,即:要求聚类空间中的一定区域内所包含对象的数目不小于某一给定阈值(Minpts).DBSCAN算法的优点是聚类速度快,且能够有效处理噪声点和发现任意形状的空间聚类[11].由于DBSCAN算法使用了全局阈值Minpts,因此,在噪声点分布密集、噪声点形成的簇中对象数目大于Minpts时,DBSCAN算法并不能识别出这类噪声点;另一方面,由于DBSCAN算法需要对数据库中的所有数据进行聚类,因此,它的执行效率不高[11].
针对以上缺陷,许多研究者提出了改进方案,文献[11]提出通过数据分区的方法来提高DBSCAN算法的效率;文献[12]提出结合对象的密度及其Eps-邻域中数据的分布特点对DBSCAN算法进行优化;文献[13]提出通过结合DBSCAN算法和中位数求方差的方法来提高DBSCAN算法的噪声点识别率.
以上改进方法在实际试验中均取得了一定的成效,但都没很好地解决DBSCAN算法在噪声点分布密集的环境下,噪声点识别率不高的问题.本文借鉴PageRank算法中网页间互相投票来解决网页TOP-N问题的思想,提出了NoiseRank算法.在DBSCAN算法基础上,通过簇间互相投票的方法,NoiseRank算法能识别出噪声点分布密集的环境下噪声点构成的簇,从而提高了噪声点分布密集的环境下噪声点识别率.
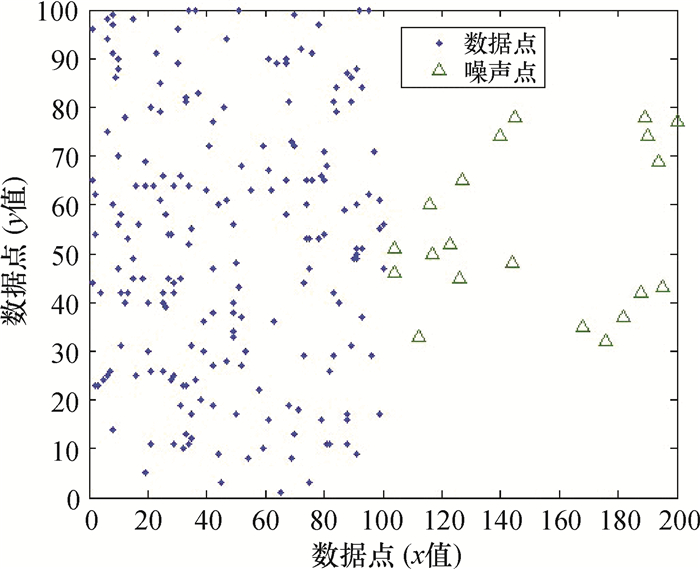
1 相关技术介绍 1.1 相关定义定义1 噪声点分布离散:设N为噪声点簇集合,n1、n2、…nm为噪声点簇,ni∈ N (1≤i≤m),n为ni(1≤i≤m)中元素个数最大值,n小于DBSCAN算法设定的Minpts,如图 1所示.
|
图 1 噪声点分布离散示意图 Figure 1 Discrete noise-data distribution |
噪声点分布离散的特点是簇内噪声点比较少,而且噪声点间的距离相对于数据点之间的距离大.
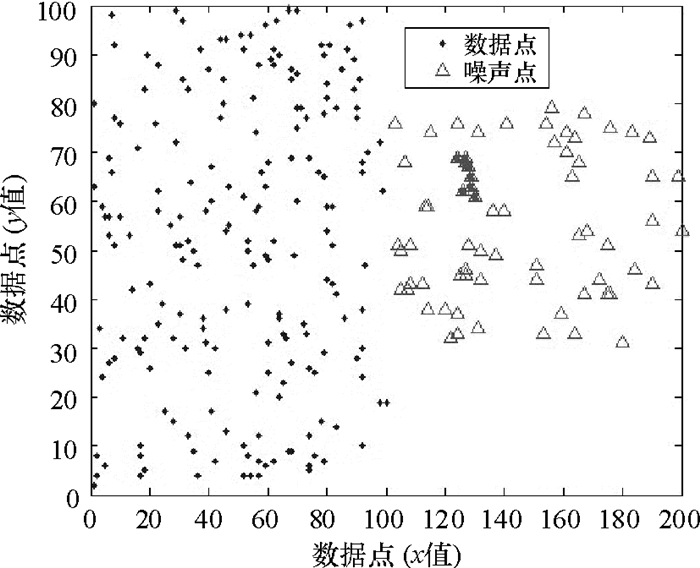
定义2 噪声点分布密集:设N为噪声点簇集合,n1、n2、nm为噪声点簇,ni∈ N (1≤i≤m),n为ni(1≤i≤m)中元素个数最大值,n大于DBSCAN算法设定的Minpts,如图 2所示.
|
图 2 噪声点密集分布示意图 Figure 2 Intensive noise-data distribution |
噪声点分布密集的特点是簇内噪声点多,而且噪声点间距离小.
定义3 簇间投票映射函数G(n, d): A簇对B簇投出自己的信任票值为:A的簇的数据点个数为n,A中心点与B中心点间的距离为d,则A簇对于B簇的投票值为G(n,d),其中G为n,d的联合函数,需要符合条件:(1)在d相同的情况下,n越大的簇对同一个簇的投票值越大;(2)在n相同的条件下,d越大的簇,对该簇的投票值越小.
1.2 已有DBSCAN及其改进算法存在的问题DBSCAN是典型的基于密度的聚类算法,将簇定义为密度相连的点的最大集合,能够把具有足够高密度的区域划分为簇,并可在有“噪声”的空间数据库中发现任意形状的聚类[13].在DBSCAN中,对于空间中的一个簇,如果它包含的元素个数不小于Minpts, 则把它识别为数据点簇;相反则识别为噪声点簇.
已有的DBSCAN及其改进算法在噪声点分布离散的环境下有着较高的噪声点识别率[11-15].由于DBSCAN算法是以Minpts作为判断数据是否为噪声点的阈值,所以当噪声点分布密集时,DBSCAN算法的噪声点识别效率并不高,如表 1所示.加入人工噪声点数量达到90后,噪声点形成了一个较大的簇,DBSCAN算法噪声点识别数目逐渐下降.
| 表 1 DBSCAN算法噪声点识别效果 Table 1 DBSCAN algorithm to identify the effect of noise-data |
PageRank算法广泛应用于搜索引擎中,大量实验证明:它能够在一定程度上避免和减少人为因素对排序结果的影响; 采用与查询无关的离线计算方式, 使其具有较高的响应速度; 一个网页只能通过别的网页对其引用来增加自身的PR值, 且算法的均分策略使得一个网页的引用越多, 被引用网页所获得的PR值就越少.因此, 算法可以有效避免那些为了提高网站的搜索排名而故意使用链接的行为[16].
受PageRank算法在搜索引擎的成功运用启示,许多研究者提出了把PageRank算法应用于web数据挖掘中,如文献[17]提出应用Web结构挖掘的PageRank算法,文献[18]提出PageRank在Web信息搜集中的应用等,均有着不错的效果.但把PageRank算法思想应用在数据挖掘中的噪声点识别领域的研究成果很少.本文将PageRank算法的推广应用于噪声点识别领域,提出NoiseRank算法.
PageRank算法使用超链接作为不同网页间的投票依据.但在数据集中,并不存在像“超链接”一样可以直接衡量不同数据点间相似度的直接依据,所以能否在数据簇间寻找到合适的相似度衡量,是PageRank能否应用到数据处理领域的关键.NoiseRank算法中通过寻找每个簇中的中心点,以每个中心点间的距离d,簇中元素数目n,通过映射函数G(n, d)计算出它们之间的相似度作为投票值.
1.4 NoiseRank算法步骤NoiseRank算法步骤如下:
(1) 使用DBSCAN算法对原始数据集进行聚类划分;
(2) 求出每个簇的中心点;
(3) 每个簇的中心点采用G(n, d)函数对其他中心点进行投票;
(4) 把投票总得分低于一定的阀值的簇中的元素标记为噪声点.
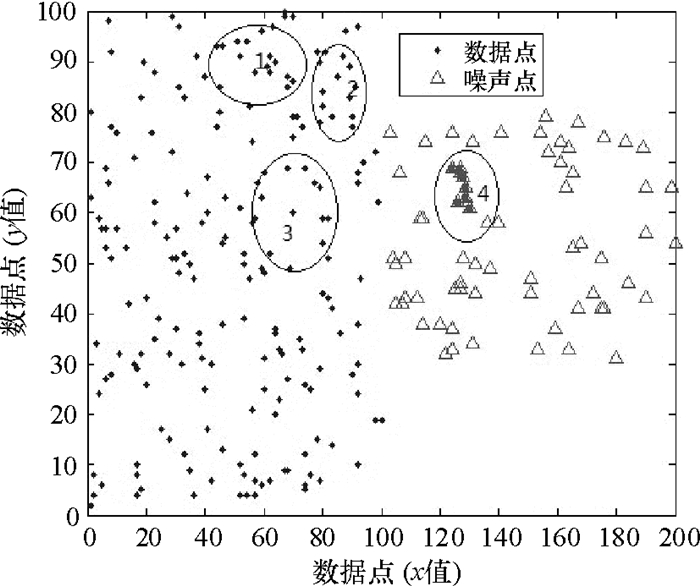
如图 3所示,存在数据点簇1、2、3,以及噪声点簇4.按照上述NoiseRank算法进行投票,每个簇通过G(n, d)函数进行投票后,依据G(n, d)函数的定义,簇1得分>簇2得分>簇3得分>簇4得分.噪声点簇4中的元素就会被NoiseRank标记为噪声点.
|
图 3 NoiseRank算法举例 Figure 3 Example of the NoiseRank algorithm |
输入:含噪声点的数据集S,S有N个数据记录,S的属性集合D={D1、D2、D3, …, Dk},S权重向量Q ={Q1、Q2、Q3、…、Qn}.
输出:噪声数据处理后的数据集合S.
说明:算法中使用的距离均是基于权值向量的距离,详细算法参考文献[1].
方法:
(1) P=DataByClustering (S, D, Q); /*在属性集合S上根据权值Q对S进行聚类得到排除孤立点后的聚类集合.*/
(2) if (P!=null){
For i=0 to length(P)
AddToCenterRecord(GetCenterRecord(P[i],Q));
}
Else
return null;
Endif/*依据权值Q计算P集合中每个数据簇的中心点并记录到CenterRecord中.如果集合P为空集合返回null.*/
(3) For k=0 to length(CenterRecord){
For j=0 to length(CenterRecord){
if(j!=k){
CenterRecord[k].Score=CenterRecord.Score+GetScore(CenterRecord(k), Center
Record[j], Q);
}/*计算其他点对k点的投票值的和.*/
}
}
(4) Noise=GetLowerRecord(CenterRecord); /*得到得分最低的簇集合*/
(5) Leader=GetHightestRrcord(CenterRecord); /*得到评分最高的记录点*/
if (Noise!= null){
For i=0 to length(Noise){
RemoveCenterRecord(i); /*不能弥合的数据簇识别为噪声簇,删除处理*/
}
}
(6) return GetRecord(CenterRecord); /*返回数据清理后的数据结果*/
其中,在使用DBSCAN或k-means等聚类算法时,DataByClustering(S, D, Q)依据权值矩阵Q计算点间距离.由于聚类算法的基本步骤类似,默认采用权值距离[7],也可以根据实际环境调整距离算法.
GetCenterRecord(p,Q)实现的是根据权值矩阵Q对簇p进行求取中心点操作.实验中的实现是依次计算p中元素与其他p中元素的距离,选择其距离之和最小的点作为p的中心点.读者也可根据自己实际情况更换中心点算法.
GetScore(CenterRecord(k), CenterRecord[j], Q)实现的是计算j簇的中心点到k簇中心点间依据权重矩阵Q计算出来的得分值,实验采用的G(n,d)函数为n关于d的反函数.
3 实验结果与分析实验数据来自加州大学的机器学习和人工智能学习研究中心,里面包含了许多数据集,实验采用的数据集可以从http://archive.ics.uci.edu/ml/datasets/Abalone处下载.
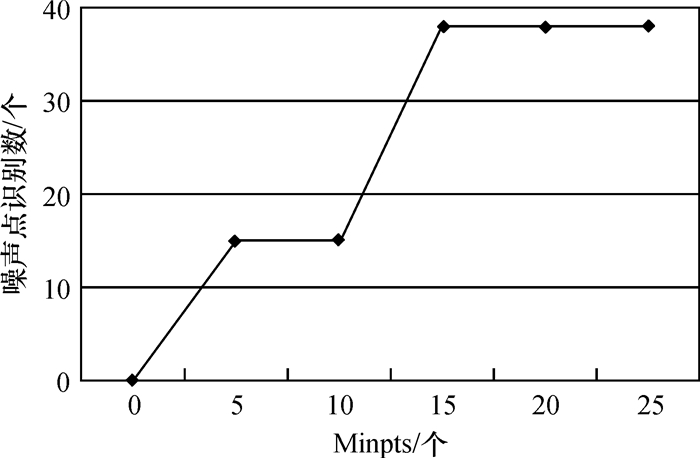
在不同Minpts下,运行DBSCAN算法,找出在测试数据集中噪声点的个数以及最佳Minpts,结果如图 4所示.在测试数据集中,以最佳Minpts为步长,通过加入人工噪声点的方法营造噪声点密集环境,运行两种算法噪声点并记录下识别噪声点数目,结果如图 5和表 2所示.
|
图 4 DBSCAN在不同Minpts下噪声点识别个数 Figure 4 Noise-data number identified by DBSCAN in different Minpts |
| 表 2 DBSCAN与NoiseRank算法识别人工噪声点对比 Table 2 DBSCAN algorithm identifies with NoiseRank artificial noise-data comparison |
从图 4中DBSCAN算法识别曲线可以得出数据集中最佳的Minpts为15,噪声点个数稳定在38.

|
图 5 DBSCAN与NoiseRank算法识别人工噪声点对比 Figure 5 Comparison of artificial noise-data identified by DBSCAN algorithm andNoiseRank |
(1) 在加入的人工噪声点小于90时,噪声点数据还未形成自己的簇,NoiseRank算法与DBSCAN算法的噪声点识别数目是相近的.
(2) 当加入的人工噪声点个数大于90时,噪声点数据形成自己的簇,DBSCAN算法的噪声点识别数目随着人工噪声点的增加而下降,在人工噪声点数目达到105,DBSCAN算法识别的噪声点仅为在人工噪声点为90的识别数目的一半.这说明DBSCAN算法在噪声点分布密集的情况下,噪声点识别率不高.
(3) 当加入的人工噪声点个数大于90时,噪声点数据形成自己的簇,随着人工噪声点数目的增加,NoiseRank算法的曲线一直在DBSCAN算法曲线之上,而且NoiseRank算法识别的噪声点数目逐渐增加,DBSCAN算法的噪声点识别数目却逐渐下降.这说明了在数据噪声点分布密集的情况下,NoiseRank算法比DBSCAN算法识别噪声点效果更好.
4 结束语本文针对DBSCAN算法在噪声点数据分布密集的环境下噪声点识别率不高的问题,借鉴PageRank算法中采用网页间投票解决TOP-N问题的方法,提出了簇间投票噪声点识别算法-NoiseRank.实验证明,NoiseRank算法在噪声点数据分布离散的环境下噪声点识别率趋近于DBSCAN算法;在噪声点数据分布密集的情况下,NoiseRank算法比DBSCAN算法有着更高的噪声点识别率.
| [1] |
滕少华, 樊继慧, 陈潇, 等. 基于KNN多组合器协同挖掘局域气象数据[J].
广东工业大学学报, 2014, 31(1): 25-31.
Teng S H, Fan J H, Chen X, et al. The Application of KNN-based Multi-classifiers in Mining Local Area Meteorological Data[J]. Journal of Guangdong University of Technology, 2014, 31(1): 25-31. |
| [2] |
张巍, 刘峰, 滕少华. 改进的Prefixspan算法及其在序列模式挖掘中的应用[J].
广东工业大学学报, 2013, 30(4): 49-54.
Zhang W, Liu F, Teng S H. Improve Prefixspan Algorithm and Its Application in Sequential Pattern Mining[J]. Journal of Guangdong University of Technology, 2013, 30(4): 49-54. |
| [3] |
Xia C Y, Hsu W, Lee M L, et al. BODER: Efficient Computation of Boundary Points[J].
IEEE Transaction on Knowledge and Data Engineering, 2006, 18(3): 289-303.
DOI: 10.1109/TKDE.2006.38. |
| [4] |
Erhar R, Hong-Hai D. Data Cleaning: Problems and Current Approaches[J].
IEEE Data Engineering Bulletin, 2000, 23(4): 3-13.
|
| [5] |
郭志懋, 周傲英. 数据质量和数据清洗研究综述[J].
软件学报, 2002, 13(11): 2076-2082.
Guo Z M, Zhou A Y. Summary of data quality and data cleansing Research[J]. Journal of Software, 2002, 13(11): 2076-2082. |
| [6] |
Bhaduri K, Matthews B L, Giannella C R. Algorithms for Speeding up Distance-based Outlier Detection[C]//Proc. of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. [S. l. ]: ACM Press, 2011.
|
| [7] |
WittenIH, FrankE, HallMA. DataMiningPractical Machine Learning Tools and Techniques[M]. [S. l.]: Morgan Kaufmann, 2011.
|
| [8] |
Guha, Rastogi R, Shim K. CURE: an Efficient Clustering Algorithm for Large Database[C]//Proceedings of the ACM SIGMOD International Conference on Management of Data, Seattle. Washington: [s. n], 1998: 73-84.
|
| [9] |
Qiu BZ, Yue F, Shen J Y. BRIM: An Efficient Boundary Points Detecting Algorithm[C]//Procofthe11thPacific-Asia Conferenceon Knowledge Discoveryand DataMining. China, Nanjing: [s. n. ], 2007: 761-768.
|
| [10] |
CastroVE, LeeI. AMOEBA: Hierarchical Clustering Basedon Spatial Proximity Using Delaunay Diagram[C]//Proc. ofthe9th International Symposium on Spatial Data Handling. China, Beijing: [s. n. ], 2000: 26-41.
|
| [11] |
周水庚, 周傲英, 曹晶. 基于数据分区的D B S C A N算法[J].
计算机研究与发展, 2000, 37(10): 1153-1159.
Zhou S G, Zhou A Y, Cao J. A data-partitioning-based dbscan algorithm[J]. Journal of Computer Research and Development, 2000, 37(10): 1153-1159. |
| [12] |
岳峰, 邱保志. 噪声数据集上的边界点检测算法[J].
计算机工程, 2007, 33(19): 82-84.
Yue F, Qiu B Z. Boundary Points Detecting Algorithm for Clusters in Noisy Dataset[J]. Computer Engineering, 2007, 33(19): 82-84. DOI: 10.3969/j.issn.1000-3428.2007.19.028. |
| [13] |
张悦, 刘杰, 李航. 一种基于概率的孤立点检测方法[J].
计算机工程, 2013, 39(3): 47-55.
Zhang Y, Liu J, Li H. An Outlier Detection Method Based on Probability[J]. Computer Engineering, 2013, 39(3): 47-55. |
| [14] |
梁斌梅, 韦琳娜, 宋庆祯. 一种基于层次聚类的全局孤立点识别方法[J].
计算机应用研究, 2011, 28(5): 1731-1733.
LiangB M, WL N, Song Q Z. Global outlier detection based on hierarchical clustering[J]. Application Research of Computers, 2011, 28(5): 1731-1733. |
| [15] |
于亚飞, 周爱武. 一种改进的DBSCAN密度算法[J].
计算机技术与发展, 2011, 21(2): 30-33, 38.
Yu Y F, Zhou A W. An Improved A lgorithm of DBSCAN[J]. ComputerTechnology and Development, 2011, 21(2): 30-33, 38. |
| [16] |
李稚楹, 杨武, 谢治军. PageRank算法研究综述[J].
计算机科学, 2011, 38(10): 185-188.
Li Z Y, Yang W, Xie Z J. Research on PageRank Algorithm[J]. Computer Science, 2011, 38(10): 185-188. |
| [17] |
范聪贤, 刘秋菊, 徐汀荣. 应用Web结构挖掘的PageRank算法的改进研究[J].
计算机工程与应用, 2010, 49(9): 127-129.
FanC X, Liu Q J, Xiu T R. Research and improve algorithm of PageRank based on Web structure mining[J]. Computer Engineering and Applications, 2010, 49(9): 127-129. |
| [18] |
秦拯, 张玲, 李娜. 改进的PageRank在Web信息搜集中的应用[J].
计算机研究与发展, 2006, 43(6): 1044-1049.
Qin Z, Zhang L, Li N. Application of an Improved PageRank in Web Crawler[J]. Journal of Computer Research andDevelopment, 2006, 43(6): 1044-1049. |
 2014, Vol. 31
2014, Vol. 31