2. 广东外语外贸大学 图书馆,广东 广州 510420
2. Library, Guangdong University of Foreign Studies, Guangzhou 510420, China
聚类分析作为信息科学、统计学、数学、机器学习等多个学科交叉而形成的一种无监督的数据分析方法,是人们探索和发现数据未知规律的重要工具.聚类分析经过几十年的发展,其理论和技术方面的研究已经逐渐成熟,出现了非常多的成果[1-2].但是,随着大数据时代的到来,需要分析的数据无论是在样本数量规模还是特征空间维度上都有极大的增加,导致许多聚类算法在应用到新的场景时很难得到理想的聚类效果.如何在大数据背景下研究更有效的聚类分析算法,是当前学术界面临的挑战.
本文在理解聚类流程的基础上,结合当前的时代背景,提出聚类分析研究中面临的新挑战和亟需解决的问题,并在相关问题上给出了未来研究的方向,期望对进一步的聚类分析研究产生一些有意义的参考.
1 聚类分析的基本框架聚类的基本思想是“物以类聚”,旨在无先验知识指导的条件下通过合理的方法将具有类似关系的数据聚集到一起,并使不同集合数据的差异性最大化[3].由此可见,数据收集和存储是聚类分析的基础,分析数据之间的同质性和差异性是聚类算法的本质.通常,在处理不同的问题时,要根据当前问题的具体情况选择合适的聚类算法,以帮助用户挖掘出潜藏在数据背后的规律或模式[4].所以,聚类分析方法会因用户需求和使用目的而有所不同,很难找到一个统一的标准对其进行分类.目前,许多研究将聚类算法大致分成基于划分的聚类算法、基于层次的聚类算法、基于图的聚类算法、基于密度和网络的聚类算法、基于约束的聚类算法以及其他聚类算法.基于划分的聚类算法以调整并确定数据对象的类别归属为目标,以优化或降低目标函数的误差值为基本判断准则[5];基于层次的聚类算法使用数据的联接规则,通过一种层次化的架构方式将数据进行多次聚合或分裂,得到一个具有层次序列结构的聚类问题解[6];基于图的聚类将待处理的数据转化成一个赋权值的无向完全图,实际上是把数据空间的关系映射到图的过程[7-8];基于密度和网络的聚类算法以样本的空间分布信息为依据,通过数据密度或网格结构来发现不同形状的簇[9];基于约束的聚类算法将领域知识或用户定义的约束条件融入到聚类算法当中,通过修改传统聚类算法的过程来限制聚类的搜索过程,使其能够处理带条件的聚类问题[10].
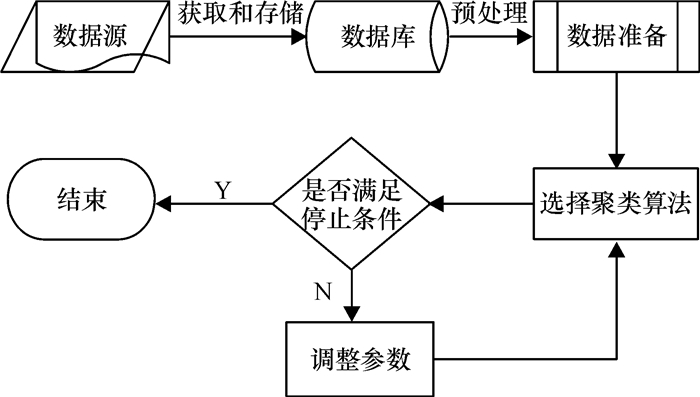
虽然已有聚类算法的研究出发点和视角有所不同,但其基本处理流程是类似的.从聚类分析的基本处理过程来看,无论哪一种聚类算法的应用都是从数据获取和存储开始,接着对数据库中的数据进行预处理,包括数据清洗、数据转换、特征表示、特征选择、差异性度量等,然后根据预处理结果选择符合挖掘目的聚类算法,最后依据该算法的停止准则对聚类算法进行优化调整以得到理想的聚类结果(上述分析过程如图 1所示).
|
图 1 聚类分析的基本框架 Figure 1 Framework of Clustering Analysis |
图 1所示的框架将聚类分析分为6个步骤,每个步骤都能直接影响聚类算法的性能,并且每个步骤都存在一些基本问题.聚类分析框架中的基本问题会对聚类效果产生关键性的作用,是研究者们一直在重点探索和关注的研究内容[11-12].
2 聚类分析研究面临的挑战聚类分析是一个富有挑战性的任务,尤其是在大数据时代,随着微博、微信等新型社会化媒体的出现,不同来源的数据一方面使数据呈现出TB级/天的增长趋势,另一方面使数据的类型变得更加多样化,使数据的结构变得更为繁杂,这些变化给聚类分析研究带来了新的困难和挑战,具体挑战包括处理多样化数据类型的能力、处理超高维数据的能力、处理不均衡数据的能力、聚类算法的可拓展能力和聚类效果评价的指标选择问题.这些挑战有的是自聚类算法产生以来就已存在,有的则是新时代产生的新问题.
2.1 处理多样化数据类型的能力随着信息技术的发展,数据的类型变得越来越复杂,同一个研究对象中可能会同时包含着多种不同类型的数据.针对不同的数据类型,研究者们提出了不同的聚类算法.不过在聚类算法产生初期,人们最先关注的是比较容易理解和处理的数值型数据.早在1967年MacQueen就针对数值型数据集提出了非常经典的K-means聚类算法,该算法以欧氏距离作为数值属性差异性的度量方法[13].K-means算法实现简单,计算速度快,处理效率高,但不能处理分类型数据.对于分类属性的数据,通常存在两种不同的处理方式,一种是将分类属性转换成多个取值为0和1的数值属性,再利用K-means算法进行处理[14];另一种是由Huang, Joshua Zhexue教授提出的适用于纯分类属性的K-modes算法,该算法采用匹配差异法度量分类属性之间的差异程度,但这种表示难以准确反映出类中对象的取值情况,导致差异性度量不准确,并且当某个属性取值频度最大的属性值多于一个时,mode不唯一,不同的mode选择可能得到完全相反的结论[15-16].事实上,在许多实际应用中,需要处理的数据中往往既含有数值型属性又包含分类型属性,此时使用K-means或K-modes算法都不能有效地解决问题.针对该问题,Huang结合K-means和K-modes算法提出了能够处理混合型属性的K-prototypes聚类算法[17],但是该方法存在着与K-modes算法一样的缺点.随后,蒋盛益针对K-prototypes聚类算法的不足,以统计频度作为分类型属性的差异性度量指标并提出了K-summary算法,该算法很好地提高了聚类效率,但是时间开销较K-prototypes有所增加[18].为了进一步提高聚类效率,在混合属性差异性度量的基础上又提出了一种基于最小距离原则的聚类算法(也称一趟聚类算法),其基本思想就是将对象依次被并入到与其差异度最小的簇中[19].一趟聚类算法只需扫描数据集一遍,具有近似线性的时间复杂度、聚类精度高的优点,可拓展性高,适用于划分大规模数据集.所以在处理大数据集时,将一趟聚类算法与其他聚类算法结合而形成的混合聚类算法或聚类融合算法则可以提高聚类效率和质量[20-22].另外,谢岳山等为解决聚类融合算法对混合属性数据处理效果不佳的问题,提出了一种基于图论的加权聚类融合算法,在聚类的基础上利用预设的融合函数对数据对象进行权重赋值,同时通过设置各个数据对间边的权重来确定数据之间的关系,并得到加权最近邻图,然后再用图论的方法进行聚类.实验表明,该算法的聚类精度和稳定性优于其他聚类融合算法[23].
上述算法都是将一个对象划分到一个簇中,属于硬聚类.但是在实际领域中,有许多对象往往同时属于多个类,所以目前有许多研究工作对上述算法进行改进形成软聚类以解决实际应用中的现实问题[24-26].尽管K-prototypes、K-summary和一趟聚类算法能够处理混合型属性,但是它们在两种不同类型属性差异性度量和比较方面的有效性还值得商榷.换句话说,在特征空间上,分类属性的取值频度与数值属性的绝对偏差在理论上是不能直接进行大小比较的.因此,如何改进不同类型属性差异度的可比性或提出更有效的混合属性差异度度量方法是未来研究的一个重要挑战.
2.2 处理超高维数据的能力在高维空间中聚类数据对象是非常有挑战性的,因为数据可能分布非常稀疏,而且会高度偏斜[27].例如,“双十一购物狂欢节”的背后隐藏着商品品牌销售量和卖家客户数量分布的不平衡性以及用户购买数据的稀疏性.传统聚类算法在处理低维数据时能够表现出较好的性能,但对于高维数据,由于属性数量过多引起的稀疏性问题和属性差异性度量的偏差问题,这往往会导致聚类效果变差.维度灾难是一个非常普遍的现象,若直接采用传统聚类算法往往不能得到所期望的结果.为了更好地满足现实需求,研究者们提出了许多针对高维数据的聚类方法.综观当前研究成果,在面对高维数据时通常都是先对特征空间进行处理,采用特征变换或特征选择的方式来降低特征维度以提高聚类算法的性能.
特征变换是根据合适的方法寻求与高维数据等价的低维空间表示,通过将原始特征空间进行变换,重新生成一个维数更小、各维度之间的独立性更强的空间,从而使降维之后的数据所包含的信息与降维之前尽可能地相同或相近[28].最常用的特征变换方法有小波变换、PCA[29]、LPP[30]和NPE[31].特征选择是在不同任务需求下选取那些符合要求且彼此之间关联程度较小的最优特征子集的过程,其目的是通过剔除与任务需求不相关和弱相关的特征以降低维度,从而提高学习算法的效率和性能[32].特征选择算法在寻找最优特征子集时,需要对特征之间的相关性进行评价.对于相同类型的特征一般采用线性相关系数、信息增益、互信息、可分性等指标来度量特征的相关性[33-34].而对于混合类型特征的相关性度量而言,通常采用的方法是将连续特征进行离散化,将混合特征之间的相关度计算转化为两个离散特征之间相关性的度量问题.离散化策略一方面会增加额外的时间开销,另一方面也可能会造成信息丢失,从而降低数据的处理效率与质量.为避免这些问题,文献[35]用均方差性质提出了一种混合特征相关性度量方法CMMF,但是如何更有效地将混合特征相关度与同类型特征间相关度进行比较也是当前需要解决的一个重要问题.
特征选择的另一种形式是子空间聚类,利用聚类算法在不同子空间中搜索簇群.目前用于处理高维数据的方法大多采用软子空间聚类,其基本思想是:在聚类时将类别看成是模糊的,即每个对象在一定程度上可以看成属于某一簇,在一定程度上又可以看成属于另一个簇,通过对数据集中的各类别赋予不同的特征权重向量,并以此来表示聚类过程中各维特征对此类别贡献的大小.在聚类过程中,不同的特征在不同的类别上有不同的贡献,因此不同的特征在不同类别有不同的特征权重向量,从而形成了若干个“软子空间”.典型软子空间聚类算法有W-K-means[36]、EWKM[37]、FWKM[38]、FCM[39]和FG-k-means[40].子空间方法多采用划分类型的聚类算法,但是这类方法一直存在着聚类个数难以确定的问题.另外,在处理混合类型数据时,子空间聚类该如何更好地分配权重向量也是一个非常难以解决的问题.
2.3 处理不均衡数据的能力随着信息技术的广泛应用,无论是科学研究还是社会生活的各个领域中都积累了大量的数据,这些数据中可能会存在某类数据对象的数量远远多于其他类别数据,或是很大部分是没有标记,只有少量是有标记的,造成数据分布出现不平衡性.在缺乏类别信息情况下,采用聚类方法就是一种有效的处理方式.而在现实生活中,大多数对象并没有严格的类别,它们在状态和类别方面存在着模糊性,因而进行软划分可能会更加真实和合理,这种现象在不均衡数据集上表现尤为突出.从大量聚类算法的实验中可以看出,相对来说,聚类算法在不均衡数据集上的性能要比在均衡数据集上的性能差.现有的划分聚类算法或层次聚类算法等在处理不均衡数据时,其聚类性能大幅度下降;部分图论聚类算法,如DBSCAN、Chameleon等能有效识别任意大小和不同形状的簇,在处理不均衡数据方面效果相对较好,但它们的时间复杂度都很高,难以处理大规模的数据集.文献[41]结合一趟聚类算法改进了DBSCAN算法,其聚类性能有了较大的提高,在处理不均衡数据方面更有优势,同时也可以应用于大规模数据集.文献[42-43]提出的两阶段混合聚类策略能比较有效地处理不均衡文档数据,文献[42]在聚类第二个阶段采用文档权重调整技术,根据文档被错误划分的次数调整文档的权值,以减少文档不平衡分布造成的影响.由于METIS图划分技术对不均衡数据处理效果欠佳,文献[43]提出使用Graclus代替METIS对不均衡数据构成的图进行图划分处理,以提高算法处理不均衡数据的性能.李志华等针对分类属性数据样本间的分布不平衡性、样本的分布与空间距离无关的特点,提出一种基于量子机制的分类属性数据模糊聚类算法.文献[44-45]通过修改传统聚类算法目标函数和加入权重系数来提高算法的鲁棒性以及在不均衡数据上的聚类性能.文献[46-47]在聚类过程中,考虑了属性的不平衡分布,对不同的分类属性赋予不同的权值以提高聚类算法的扩展性.另外,集成学习和数据抽样也是解决不均衡数据聚类的有效方式,它们通过投票机制或抽样训练的方式改进原始数据的分布结构以降低不均衡性[48-49].
虽然在不均衡数据的处理问题上存在着多种解决方式,但是在对待具体大规模数据时,其算法的效率和效果都有待进一步分析和验证.所以,针对不均衡数据的高性能聚类算法研究也是一个有待深入研究的问题.
2.4 聚类算法的可拓展能力许多聚类算法在小样本数据集上能够表现出很好的性能,但对包含几百万甚至上亿个数据对象的大规模数据集进行聚类可能会产生有偏的结果.因为不同类型的聚类算法都存在着各自的问题:划分聚类算法中聚类数目的选择和聚类初始点的选择是影响算法性能的关键和难点;层次聚类算法虽然不需要预先指定聚类数目,但是它在运行过程中不能回溯处理已经形成的簇结构,且时间复杂度非常高;基于图论的聚类算法易于发现不规则的簇,但图的最优划分是一个NP难问题;基于网络和密度的聚类算法需要预先指定较多参数.上述问题都是影响聚类算法的可扩展性的重要因素,但目前也有不少研究针对这些问题对部分聚类算法进行改进以提高其拓展性.文献[50]提出了一种面向最小包含球问题的核心集求解算法,该算法所得核心集的大小与数据集的维数和大小均无关.文献[51]将该技术用于谱聚类,提出了新的适用于大规模数据集的谱聚类算法.文献[52]结合增量聚类方法对G-K-Means算法进行改进,该算法需要最小化辅助聚类函数.而文献[53]和[54]分别在聚类数目确定和聚类初始点的选择方面给出有指导性的处理方式,并使它们能拓展至大规模数据集上.最近,Tzortzis等通过对各个簇指派不同的权重值以寻找到最优的初始聚类点,实验证明该方法具有较好的拓展性,能够应用于大规模数据集[55].尽管许多聚类算法在经过改进之后能够在一定程度上适用于大规模数据集,但是在面对超大规模的数据集时,还需要研究更有效的、拓展性更好的聚类算法.
2.5 聚类效果评价的指标选择问题聚类算法产生已经有几十年了,但是关于聚类算法的评估问题仍然是一个尚需突破的难题.聚类算法的常见评估指标包括外部评估指标和内部评估指标.外部评估方法是有监督的方法,与聚类算法无关.理想的聚类结果是:具有相同类别的数据对象被聚集到相同的簇中,不同类别的数据对象聚集在不同的簇中,主要的指标有聚类熵、聚类精度和召回率等.聚类熵考虑簇中不同类别数据的分布,聚类熵越小,聚类效果越好.聚类精度的基本出发点是使用簇中数目最多的类别作为该簇的类别标记.聚类召回率能够反映被正确聚类的对象的比率.内部评估方法是利用未知结构数据集的固有特征和量值来进行评价,主要通过考察簇的分离情况和簇的紧凑情况评估聚类效果,常用的指标有SSE、Cophenetic相关系数和stability等[56].此外,聚类数目也是评估算法性能的一个重要指标.一般而言,SSE、stability、聚类熵、聚类簇个数和召回率之间一致性较好,但不绝对,而这些指标往往都和聚类精度有冲突.特别是在进行大数据聚类时,需要聚类成多个簇,需要达到什么样的效果才能有效解决实际问题,这些都需要结合聚类任务以及其他知识进行综合考量.所以,在评价聚类算法的性能时,一般需要根据任务需求选择合适的评估指标.由此可见,解决评估指标之间的矛盾也是一个大挑战,而如何衡量聚类数目以及其他聚类效果评估指标之间的关系是未来需要加强研究的方向.
3 结论聚类分析作为典型的无监督学习方法,是探索数据规律的一种有效工具,也可作为其他学习分析方法的预处理步骤,具有非常广泛的应用价值.本文从理解聚类分析的基本框架出发,将聚类过程分成6个步骤,然后分别就聚类分析框架中各个步骤产生的挑战性问题及解决方法进行了归纳和总结, 并提出了未来研究的方向.
当然,对于大数据环境下的聚类分析而言,还有一些始终未能解决的或将会出现的挑战性问题的存在.因此,在未来的研究工作中需要进一步解决已存在的挑战性问题, 并对新出现的问题开展更多有针对性的研究,以期进一步丰富聚类分析的研究内容和拓展聚类分析的研究方向.
| [1] |
Pradeep R, Shubha S. A survey of clustering techniques[J].
International Journal of Computer Applications, 2010, 7(12): 1-5.
DOI: 10.5120/ijca. |
| [2] |
Reddy B, Ussenaiah M, Mani M, et al. Literature survey on clustering techniques[J].
Journal of Computer Engineering, 2012, 3(1): 1-12.
|
| [3] |
Xu R, Wunsch D. Survey of clustering algorithms[J].
IEEE Transactions on neural networks, 2005, 16(3): 645-678.
DOI: 10.1109/TNN.2005.845141. |
| [4] |
孙吉贵, 刘杰, 赵连宇. 聚类算法研究[J].
软件学报, 2008, 19(1): 48-61.
Sun J G, Liu J, Zhao L Y. Clustering algorithms research[J]. Journal of Software, 2008, 19(1): 48-61. |
| [5] |
王骏, 王士同. 基于混合距离学习的双指数模糊C均值算法[J].
软件学报, 2010, 21(8): 1878-1888.
Wang J, Wang S T. A dsouble-indexed FCM algorithm based on hybrid distance metric learning[J]. Journal of Software, 2010, 21(8): 1878-1888. |
| [6] |
Cilibrasi R L, Vitányi P MB. A fast quartet tree heuristic for hierarchical clustering[J].
Pattern Recognition, 2011, 44(3): 662-677.
DOI: 10.1016/j.patcog.2010.08.033. |
| [7] |
Schaeffer S E. Graph clustering[J].
Computer Science Review, 2007, 1(1): 27-64.
DOI: 10.1016/j.cosrev.2007.05.001. |
| [8] |
Dhanjal C, Gaudel R, Clémençon S. Efficient eigen-updating for spectral graph clustering[J].
Neurocomputing, 2014, 131: 440-452.
DOI: 10.1016/j.neucom.2013.11.015. |
| [9] |
Birant D, Kut A. ST-DBSCAN: An algorithm for clustering spatial-temporal data[J].
Data & Knowledge Engineering, 2007, 60(1): 208-221.
|
| [10] |
尹学松, 胡思良, 陈松灿. 基于成对约束的判别型半监督聚类分析[J].
软件学报, 2008, 19(11): 2791-2802.
Yi X S, Hu S L, Chen S C. Discriminative semi-supervised clustering analysis with pairwise constraints[J]. Journal of Software, 2008, 19(11): 2791-2802. |
| [11] |
褚娜, 马利庄, 王彦. 聚类趋势问题的研究综述[J].
计算机应用研究, 2009, 26(3): 801-803.
Chu N, Ma L Z, Wang Y. Research for clustering tendency[J]. Application Research of Computers, 2009, 26(3): 801-803. |
| [12] |
王骏, 王士同, 邓赵红. 聚类分析研究中的若干问题[J].
控制与决策, 2012, 27(3): 321-328.
Wang J, Wang S T, Deng Z H. Survey on challenges in clustering analysis research[J]. Control and Decision, 2012, 27(3): 321-328. |
| [13] |
MacQueen J. Some methods for classification and analysis of multivariate observations[C]//Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. Calif Berkeley: [s. n], 1967, 1(14): 281-297.
|
| [14] |
Ralambondrainy H. A conceptual version of the K-means algorithm[J].
Pattern Recognition Letters, 1995, 16(11): 1147-1157.
DOI: 10.1016/0167-8655(95)00075-R. |
| [15] |
Huang J. A fast clustering algorithm to cluster very large categorical data sets in data mining[C]//Proceedings of SIGMOD Workshop on Research Issues on Data Mining and Knowledge Discovery. Australian Canberra: [s. n], 1997: 1-8.
|
| [16] |
Huang Z, Ng M. A note on k-modes clustering[J].
Journal of Classification, 2003, 20(2): 257-261.
DOI: 10.1007/s00357-003-0014-4. |
| [17] |
Huang Z. Extensions to the k-means algorithm for clustering large data sets with categorical values[J].
International Journal of Data Mining and Knowledge Discovery, 1998, 2(3): 283-304.
DOI: 10.1023/A:1009769707641. |
| [18] |
蒋盛益, 李庆华. 一种增强的k-means聚类算法[J].
计算机工程与科学, 2006, 11: 56-59.
Jiang S Y, Li Q H. An enhanced k-means clustering algorithm[J]. Computer Engineering & Science, 2006, 11: 56-59. |
| [19] |
Jiang S, Song X, Wang H, et al. A clustering-based method for unsupervised intrusion detections[J].
Pattern Recognition Letters, 2006, 27(7): 802-810.
DOI: 10.1016/j.patrec.2005.11.007. |
| [20] |
李霞, 蒋盛益, 张倩生, 等. 适用于大规模文本处理的动态密度聚类算法[J].
北京大学学报:自然科学版, 2013, 49(1): 133-139.
Li X, Jiang S Y, Zhang Q S. A dynamic density-based clustering algorithm appropriate to large-scale text processing[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2013, 49(1): 133-139. |
| [21] |
蒋盛益, 庞观松, 张黎莎. Chameleon算法的改进[J].
小型微型计算机系统, 2010, 31(8): 1643-1646.
Jiang S Y, Pang G S, Zhang L S. Enhanced chameleon clustering algorithm[J]. Journal of Chinese Computer Systems, 2010, 31(8): 1643-1646. |
| [22] |
Jiang S, Pang G, Wu M, et al. An improved K-nearest-neighbor algorithm for text categorization[J].
Expert Systems with Applications, 2012, 39(1): 1503-1509.
DOI: 10.1016/j.eswa.2011.08.040. |
| [23] |
谢岳山, 樊晓平, 廖志芳, 等. 一种基于图论的加权聚类融合算法[J].
计算机应用研究, 2013, 30(4): 1015-1016.
Xie Y S, Fan X P, Liao Z F, et al. Weight cluster fusion algorithm based graph[J]. Application Research of Computer, 2013, 30(4): 1015-1016. |
| [24] |
Huang Z, Ng M. A Fuzzy k-modes Algorithm for Clustering Categorical Data[J].
IEEE Transactions on Fuzzy Systems, 1999, 7(4): 446-452.
DOI: 10.1109/91.784206. |
| [25] |
Chen N, Chen A, Zhou L. Fuzzy K-prototypes algorithm for clustering mixed numeric and categorical valued data[J].
Journal of Soft ware, 2001, 12(8): 1107-1119.
|
| [26] |
Yu J, Yang M. Optimality test for generalized FCM and its application to parameter selection[J].
IEEE Transactions on Fuzzy Systems, 2005, 13(1): 164-176.
DOI: 10.1109/TFUZZ.2004.836065. |
| [27] |
贺玲, 蔡益朝, 杨征. 高维数据聚类方法综述[J].
计算机应用研究, 2010, 27(1): 23-26.
He L, Cai Y C, Yang Z. Survey of clustering algorithms for high-dimensional data[J]. Application Research of Computers, 2010, 27(1): 23-26. |
| [28] |
Jain A. Data clustering: 50 years beyond K-means[J].
Pattern Recognition Letters, 2010, 31: 651-666.
DOI: 10.1016/j.patrec.2009.09.011. |
| [29] |
Scholkopf B, Smola A, Muller K. Nonlinear component analysis as a kernel eigenvalue problem[J].
Neural Computation, 1998, 10(5): 1299-1319.
DOI: 10.1162/089976698300017467. |
| [30] |
He X, Niyogi P. Locality preserving projections[C]//Advances in Neural Information Processing Systems 16. Cambridge MA: MIT Press, 2004: 585-591.
|
| [31] |
He X, Cai D, Yan S, et al. Neighborhood preserving embedding[C]//Proceedings of the Tenth IEEE Int Conf on Computer Vision. Washington DC: IEEE Computer Society, 2005: 208-1213.
|
| [32] |
Jiang S, Wang L. An unsupervised feature selection framework based on clustering[C]//New Frontiers in Applied Data Mining, Springer Berlin Heidelberg, 2012: 339-350.
|
| [33] |
Mitra P, Murthy C, Pal S. Unsupervised feature selection using feature similarity[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002: 301-312.
|
| [34] |
Jiang S, Wang L. Unsupervised feature selection based on clustering[C]//The IEEE Fifth International Conference on Bio-Inspired Computing: Theories and Applications. China, Changsha: [s. n], 2010: 263-270.
|
| [35] |
王连喜, 蒋盛益. 一种基于类别区分互补性的特征选择[J].
小型微型计算机系统, 2013, 4(8): 1798-1802.
Wang L X, Jiang S Y. A categorical discriminate complemental-based feature selection[J]. Journal of Chinese Computer Systems, 2013, 4(8): 1798-1802. |
| [36] |
Huang J, Ng M, Rong H, et al. Automated variable weighting in k-means type clustering[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(5): 657-668.
DOI: 10.1109/TPAMI.2005.95. |
| [37] |
Jing L, Ng M, Huang J. An entropy weighting k-means algorithm for subspace clustering of high-dimensional sparse data[J].
IEEE Transactions on Knowledge and Data Engineering, 2007, 19(8): 1026-1041.
DOI: 10.1109/TKDE.2007.1048. |
| [38] |
Jing L, Ng M, Xu J, et al. Subspace clustering of text documents with feature weighting K-means algorithm[C]// Proceedings of the 9th Pacific-Asia Conference on Knowledge Discovery and Data Mining. Berlin Heidelberg: Springer, 2005: 802-812.
|
| [39] |
王丽娟, 关守义, 王晓龙, 等. 基于属性权重的Fuzzy C Mean算法[J].
计算机学报, 2006, 29(10): 1797-1803.
Wang L J, Guan S Y, Wang X L, et al. Fuzzy C mean algorithm based on feature weights[J]. Chinese Journal of Computers, 2006, 29(10): 1797-1803. DOI: 10.3321/j.issn:0254-4164.2006.10.009. |
| [40] |
Chen X, Ye Y, Xu X, et al. A feature group weighting method for subspace clustering of high-dimensional data[J].
Pattern Recognition, 2012, 45(1): 434-446.
DOI: 10.1016/j.patcog.2011.06.004. |
| [41] |
Jiang S, Li X. A hybrid clustering algorithm[C]//In: Sixth International Conference on Fuzzy Systems and Knowledge Discovery. China, Tianjin: [s. n], 2009, 1: 366-370.
|
| [42] |
刘铭, 王晓龙, 刘远超. 基于语义的高维数据聚类技术[J].
电子学报, 2009, 37(5): 925-929.
Liu M, Wang X L, Liu Y C. Clustering technology for high dimensional data based on semantics[J]. Acta Electronic Sinica, 2009, 37(5): 925-929. |
| [43] |
Bilgin T, Camurcu A. A clustering framework for unbalanced partitioning and outlier filtering on high dimensional datasets[C]//Advances in Databases and Information Systems. Berlin Heidelberg: Springer, 2007: 205-216.
|
| [44] |
李志华, 王士同. 一种基于量子机制的分类属性数据模糊聚类算法[J].
系统仿真学报, 2008, 20(8): 2119-2122.
Li Z H, Wang S T. Fuzzy clustering algorithm for categorical data using quantum mechanics[J]. Journal of System Simulation, 2008, 20(8): 2119-2122. |
| [45] |
黄鹏飞, 张道强. 拉普拉斯加权聚类算法[J].
电子学报, 2008, 36(12A): 50-54.
Huang P F, Zhang D Q. Weighted Laplacian clustering algorithm[J]. Acta Electronic Sinica, 2008, 36(12A): 50-54. |
| [46] |
Yu J, Yang M, Lee E. Sample-weighted clustering methods[J].
Computers & Mathematics with Applications, 2011, 62(5): 2200-2208.
|
| [47] |
Chen J, Yang Z, Yin J, et al. An incremental clustering with attribute unbalance considered for categorical data[M]. Berlin Heidelberg: Springer, 2009: 433-442.
|
| [48] |
蒋盛益, 苗邦, 王连喜. 面向不平衡数据的特征加权聚类算法[J].
小型微型计算机系统, 2013, 34(8): 1809-1812.
Jiang S Y, Miao B, Wang L X. Feature weighted clustering algorithm for unbalanced data[J]. Journal of Chinese Computer Systems, 2013, 34(8): 1809-1812. |
| [49] |
蒋盛益. 基于投票机制的融合聚类算法[J].
小型微型计算机系统, 2007, 28(2): 306-309.
Jiang S Y. Cluster fusion algorithm based on majority voting mechanism[J]. Journal of Chinese Computer Systems, 2007, 28(2): 306-309. |
| [50] |
Badoiu M, Clarkson K. Optimal core-sets for balls[J].
Computational Geometry, 2008, 40(1): 14-22.
|
| [51] |
钱鹏江, 王士同, 邓赵红. 基于最小包含球的大样本数据集快速谱聚类算法[J].
电子学报, 2010, 38(9): 2035-2041.
Qian P J, Wang S T, Deng Z H. Fast spectral clustering for large datasets using minimal enclosing Ball[J]. Acta Electronic Sinica, 2010, 38(9): 2035-2041. |
| [52] |
Bagirov A, Ugon J, Webb D. Fast modified global k-means algorithm for incremental cluster construction[J].
Pattern Recognition, 2011, 44(4): 866-876.
DOI: 10.1016/j.patcog.2010.10.018. |
| [53] |
Kalogeratos A, Likas A. Dip-means: an incremental clustering method for estimating the number of clusters[C]//in: Advances in Neural Information Processing Systems. USA Nevada: [s. n], 2012: 2402-2410.
|
| [54] |
Celebi M, Kingravi H, Vela P. A comparative study of efficient initialization methods for the k-means clustering algorithm[J].
Expert Systems with Applications, 2013, 40(1): 200-210.
DOI: 10.1016/j.eswa.2012.07.021. |
| [55] |
Tzortzis G, Likas A. The MinMax k-Means clustering algorithm[J].
Pattern Recognition, 2014, 47: 2505-2516.
DOI: 10.1016/j.patcog.2014.01.015. |
| [56] |
Shamir O, Tishby N. Cluster stability for finite samples[C]//Advances in Neural Information Processing Systems. Cambridge MA: MIT Press, 2008: 1297-1304.
|
 2014, Vol. 31
2014, Vol. 31