随着大数据时代到来,3G网络建设和商用不断深入,电信业正从服务经济向体验经济转型,移动网络运营商之间的竞争也已从市场竞争转向服务竞争.保障网络通信质量、提升网络服务质量是运营商掌握竞争先机所必须考虑的问题.
Reicheld的调查报告显示,每增加5%的客户保持率,行业就会增加25%~95%的平均利润率[1].因此,如何为客户群体提供优质服务,保持客户,避免客户流失,是各大企业的核心工作任务.为了准确地了解客户、分析客户、服务客户,企业首先要正确地划分客户群体.通过客户细分, 运营商能更好地识别客户群体, 对不同的客户, 采取不一样的客户保持策略, 达到最优化配置与利用资源,最大化获取利润的目的.
1 相关工作张巍等[2]从电信业务出发,按用户行为、用户类型、用户投诉等多个角度细分用户,探讨了移动网络语音业务用户体验的建模问题,给出了建模方案.徐猛[3]探讨了面向用户体验的多QoS约束多流程调度算法,目的是满足尽可能多的用户QoS需求,但未涉及基于用户体验的协同建模问题.周天圆[4]将决策树、模糊神经网络等算法用来分析电信业务的用户体验,研究结果用现网数据进行了验证,但未对具体建模过程进行描述.郑茜茜[5]将客户数据根据某个给定的阈值划分群体,阈值直接决定了划分效果的好坏.通常阈值的确定需要经过专家仔细研究和分析.但是,在不同地区和不同人文地理环境下,客户群体的划分往往不同,传统的通过某种阈值的统计分析法很难做到准确地细分客户群体.
在运用数据挖掘方法细分客户群体中,常用的是基于划分的K-means聚类[6].K-means聚类简单、易行,时间复杂度是O(tKmn)[7],其中t为迭代次数,K为类别数,m为样本维数,n为样本数,K-means聚类的时间复杂度和样本数成线性关系,因此可用于大数据的客户细分.王扶东等[8]从客户生命周期价值方面考虑,提出了基于加权的K-means客户细分方法.但是,K-means聚类算法对初始聚类中心的选取依赖性极大,较差的初始聚类中心常导致算法陷入局部最优解[6].
国内外许多研究集中于降低初始聚类簇中心的选择对算法结果的影响,杜巍等[9]研究初始聚类中心的选取方法,提出了一个改进的K-means聚类方法,并应用于客户细分,获得了一些有益的结果.Md.SohrabMahmud等[10]基于平均权重,提出了一个初始化聚类中心的方法.王令剑等[11]将聚类方法和时间序列分析结合,并用于入侵检测中,通过实验验证了该方法的有效性.曹永春[12]将改进的人工蜂群算法和K-means迭代相结合,降低了初始聚类中心的依赖性和陷入局部最优解的可能性.胡伟[13]提出了一个层次聚类的思路,通过从上往下地构造一棵K均值聚类树,最终在叶子节点达到聚类结果.高灵渲等[14]在K-means算法的欧氏距离及中心点判定阶段改进, 提升了K-means算法的效率.易倩等[15]将马氏距离与K-means算法相结合, 并在目标函数中增加变量权重因子和协方差矩阵调节因子,提高了聚类精度.杜红乐等[16]针对数据之间距离不均匀的问题,研究了模糊C均值聚类问题及其应用.
上述研究在一定程度上对初始聚类中心的确定有所帮助,但尚未有效解决K-means算法依赖于初始聚类中心的问题.
除了初始聚类中心的影响外,K-means算法对噪声点和离群点很敏感.廖松有等[17]通过引入模糊熵约束,使用了模糊C均值聚类算法,在一定程度上能抑制噪声数据对聚类的影响.卢鹏丽等[18]以密度敏感距离作为相似性测度,结合近邻传播聚类算法和谱聚类算法,提出了一种密度敏感的层次化聚类算法.潘章明[19]基于分治策略,提出了一种改进的共享近邻聚类算法.这些算法都是从密度的角度研究噪声点和离群点.
国内外学者针对K-means聚类方法及其应用,开展了一系列研究,取得了许多成果,但下列问题尚未得到有效解决.
(1) 初始聚类中心选取:初始聚类中心选取不合适,会导致局部最优解;
(2) 聚类个数K:有时用户需要聚类成不同个数的簇.同一个数据集,从不同的角度分析将需要不同的聚类个数,产生不同的聚类效果,比如评价可分为好、中、及格、差,也可分为很好、好、中、及格、差、极差等;
(3) 聚类效果:由于聚类受初始簇中心选取和K值影响,聚类结果往往难以保证.
为此,本文提出可调多趟聚类方法,第1趟通过引入一个较大的K值,采用K-means聚类算法,获得K个簇,为第2趟聚类的簇数及簇中心初始值选择提供参考.由此,用户可以根据实际情况,选择合适的簇数及初始簇中心,通过第2趟聚类获取较好的挖掘结果.
2 K-means聚类K-means聚类算法是1967年由MacQueen首次提出的一种经典划分聚类方法.K-means算法以K为参数,把n个数据对象的集合分为K个簇,使得簇内对象的相似度高,簇间对象的相似度低.簇的相似度是关于簇中对象的均值度量,如质心、重心、距离等.本文采用欧氏距离计算.
K-means算法流程如下:首先,随机地选择K个对象,每个对象代表一个簇的初始簇中心.对剩余的每个对象,根据其与各个簇中心的距离,将它指派到最相似的簇.然后计算每个簇的新均值.这个过程不断重复,直到准则函数收敛.
定义1[6] 平方误差准则函数.设x是多维空间中的点,表示给定对象:mi是簇Ci的簇中心,d()表示两个对象之间的距离(通常采用欧氏距离),平方误差和SSE定义为:
| $ {\rm{SSE = }}\sum\limits_{i = 1}^k {\sum\limits_{x \in {C_i}} {d{{\left( {{m_i}, x} \right)}^2}} } . $ | (1) |
基于距离的K-means聚类算法存在以下不足:算法需要预先给定簇个数K;算法对初始簇中心值选取依赖性极大,常陷入局部最优;在数据量小的情况下,算法对离群点和噪声很敏感;算法不能用于发现非凸形状的簇;算法只能用于数值数据.
K-means聚类算法需要预先给定簇个数,这一特点限制了对基于客户细分的用户业务分析.有时,用户希望从多个角度对数据进行分析,希望将客户细分为不同的级别,以便进行不同级别上的决策.例如某企业决策层希望把客户细分为潜在流失客户、一般客户和VIP客户3个类别;而具体业务人员希望把客户细分为潜在流失客户、可挽留客户、一般客户、可升级客户和VIP客户5个类别.这时,K-means聚类方法需要开展两次完全无关的挖掘,并且在大数据下,难以保证挖掘的效果.针对K-means存在的不足,并兼顾不同用户的需求,本文在进行大量数据挖掘实践的基础上,提出了一个可调的多趟K-means聚类方法.
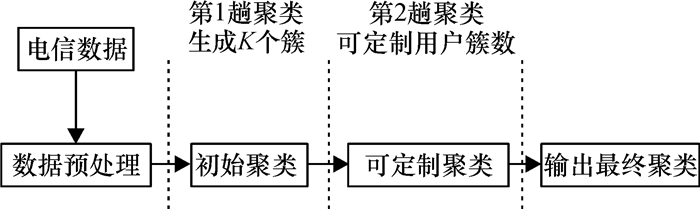
3 可调的多趟K-means聚类本文的多趟K-means聚类分为两趟,第1趟确定初始簇,为用户选择K值和初始簇中心提供依据与参考.第2趟为可定制的聚类.其体系结构如图 1所示.
|
图 1 可调多趟聚类过程 Figure 1 The adjustable multi-times clustering process |
层次聚类分为自顶向下和自底向上两种.本文提出的聚类算法采用自底向上的方式,初始聚类从用户期望分类的簇数出发.聚类过程如下:
(1) 获取电信业务数据集D,对数据进行预处理;
(2) 根据用户实际需要,获取聚类簇数K0(K0为整数);
(3) 依据专家知识、背景和用户需求将簇数K0放大到聚类簇数K1(
(4) 从D中任选K1个数据对象作为初始聚类中心;
(5) 对数据集D做K1-means聚类;
(6) 生成大约K1个聚类簇.
初始聚类时,由于选取了多个聚类中心,随机性强,覆盖面广,能够在一定程度上避免选取不合适的聚类中心,导致聚类效果进入局部最优.
初始聚类后,可以用误差平方和、抱团性和分离性等评价指标分析是否有离群簇.
3.2 可定制的K-means聚类可定制的K-means聚类,可通过用户需求、反复实验及历史经验,用多个K值调整目标聚类个数.例如可设置聚类个数为K-2、K-1、K、K+1、K+2,然后比较哪组聚类的效果较优,根据实际需要作出合适的选择.
第2趟聚类在第1趟聚类基础上,选取K个值作为第2趟初始簇中心,它们是距离最远的K个第1趟的簇中心,以避免聚类中心在迭代过程中重合,导致局部最优解.第2趟聚类过程如下:
(1) 获取第1趟聚类中心C1、C2、…、CK1;
(2) 计算任意两个簇中心Ci与Cj之间的距离DISTij;
(3) 取K个不同的Ci值(i=1, 2, …, K),计算
| $ \max \sum\limits_{i = 1}^K {\sum\limits_{j = 1}^{K_1} {\left[{\left. {{\rm{DIST}}\left( {{C_i}, {C_j}} \right)} \right)} \right]} } ; $ | (2) |
(4) 将满足式(2)的K个Ci作为第2趟的初始聚类中心;
(5) 对数据集D做K-means聚类;
(6) 最后根据聚类结果合并簇,得到目标划分.
在聚类过程中,满足式(2)的K个不同的Ci值,确保了K个初始簇中心两两之间的距离较大,避免聚类中心在迭代过程中重合.
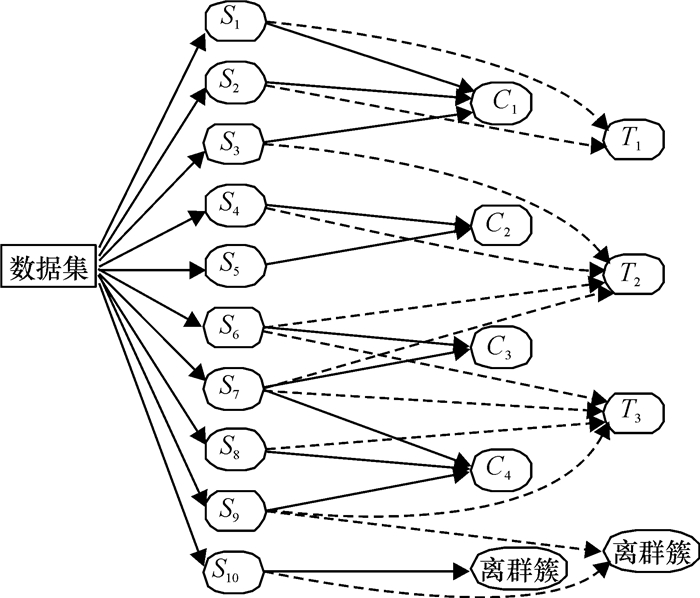
3.3 可调的多趟聚类效果可调的多趟聚类效果如图 2所示.第1趟产生K1个簇,第2趟用户可定制K个簇.在图 2中,Si(i= 1, 2, …, n)为第1趟聚类的簇;Ci与Ti分别为用户根据不同需求定制的簇.
|
图 2 可调多趟聚类结果示意图 Figure 2 Diagram of the adjustable multi-times culstering results |
本文的可调多趟聚类算法如下.设用户需要划分K0个簇,数据集为X={x1,x2,x3,…,xi,…,xn},其中xi是一条数据记录,算法的步骤如下:
(1) 设定K1个初始聚类中心,K1远大于K0,可以取K1 =5×K0.
(2) 根据K1个聚类中心,对X做K1-means聚类,得到K1个簇.
(3) 分析K1个簇,判断是否有离群簇.如果有离群簇,在X中分离对应的离群簇数据.
(4) 假设除离群簇外有K2个簇中心C={c1,c2,c3,…,cK2}.计算两两簇中心之间的距离.
(5) 计算
(6) 选择前K0个不同的Ci,满足式(2)的要求,将Ci作为第2趟聚类的初始簇中心.
(7) 对数据集用K0个Ci做K0-means聚类.得到K0个簇G={g1,g2,g3,…,gK0}.
(8) 将步骤7的聚类结果输出.
(9) 根据需要修改K0值,即改变目标聚类个数,重复步骤6~8.
步骤8对得到的多组聚类结果进行对比和评估,根据实际情况选择合适的聚类结果.
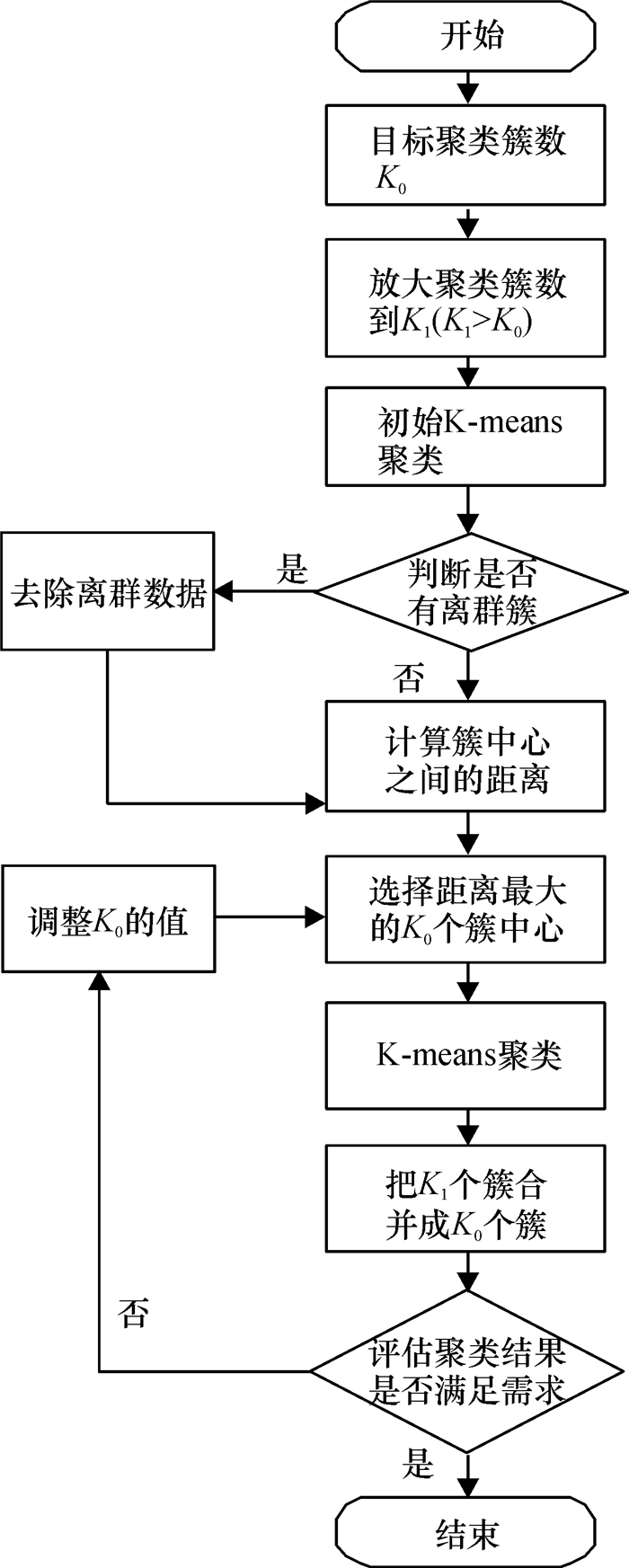
算法流程如图 3所示.
|
图 3 算法流程图 Figure 3 The flowchart of the adjustable multi-times clustering algorithm |
使用可调的多趟K-means聚类能够排除离群簇,减少了初始聚类中心对聚类结果的影响,并能发现非凸形状的簇,最后还能够根据实际需要调整聚类个数.本文的方法适合于用户对聚类数及聚类结果都比较模糊,可为用户提供多种聚类效果的选择.
3.5 算法评估聚类算法能够使簇内具有较高的相似度,而簇与簇之间的相似度较低.为了分析聚类的效果,需要从簇中对象的“相似性”和不同簇之间对象的“相异性”两方面考虑,可按定义1的评价方法来衡量算法的有效性.
平方误差和,用于评价簇的集中程度.小的平方误差和说明簇中的对象集中度高.平方误差和的计算参见定义1.
分离性,即任意两个簇中心的距离中的最小值[13].分离性值越大,簇与簇之间相差越大.分离性的定义如下:
定义2[13] 分离性.设Ci为簇i(i=1, 2, …, k)的簇中心,分离性定义为
| $ F = \mathop {\min }\limits_{\begin{array}{*{20}{c}} {i = 1,2, \cdots ,k}\\ {j = 1,2, \cdots ,k} \end{array}} \left( {{c_i} - {c_j}} \right) $ | (3) |
为了验证可调多趟K-means聚类方法在客户细分中的可行性和有效性,本文用某电信企业的移动用户数据进行了实验,并对实验结果做了分析和总结.
本实验数据采用电信客户的通话数据,根据客户的通话质量情况细分客户.实验中把客户分为5个等级,通信质量好、通信质量较好、通信质量中、通信质量较差、通信质量差,分别代表 5个等级的服务情况.对于通信质量较差与差的客户,移动运营商应该着重改善该客户群体的服务质量,防止客户流失;对于通信质量好及较好的客户,移动运营商可以有针对性地为他们提供额外的服务,引导该客户群体提升消费水平.
客户的通话数据来源于测量报告,如表 1所示.数据中包括客户标识、上下行接收电平、接收质量、时间提前量等反映网络质量水平的数据.在GSM网络[20-21]中误码率(RxQual)和上、下行电平(Rxlev)是影响通话质量的重要因素.误码率决定了通话时的语音质量.误码率也称作质量,其值越小,语音质量越好.上、下行电平反应手机的信号好坏.当上、下行电平太低时,可能会导致手机信号弱,无法进行电话的正常拨打和接听.当上、下行电平不平衡时,也可能会导致频繁的掉话.
| 表 1 测量报告的主要数据及说明 Table 1 Main data and instructions in measurement reports |
实验环境采用数学软件Matlab,实验选取了测量报告中与网络质量相关的11条属性做分析,构成了8组数据集,数据集的数据量从11322条到82665条.
以最后一组数据为例,实验使用可调多趟K-means聚类方法,对82665条数据进行聚类.由于需要把客户分为5个等级,所以设定第1次聚类个数为20倍,即100个.聚类后分析,得到1个离群簇,离群簇中包含数据609条.排除这609条离群数据后进行第2次聚类,对99个簇中心施行可定制的聚类.经过实验对比和用户实际需求,决定第2次聚类个数为5个.这样定制后聚类簇数为5个簇,这5个簇分别对应通信质量好、通信质量较好、通信质量中、通信质量较差和通信质量差,合并后每个簇的数据量分别是40 869、26 300、8 879、2 930、3 078.
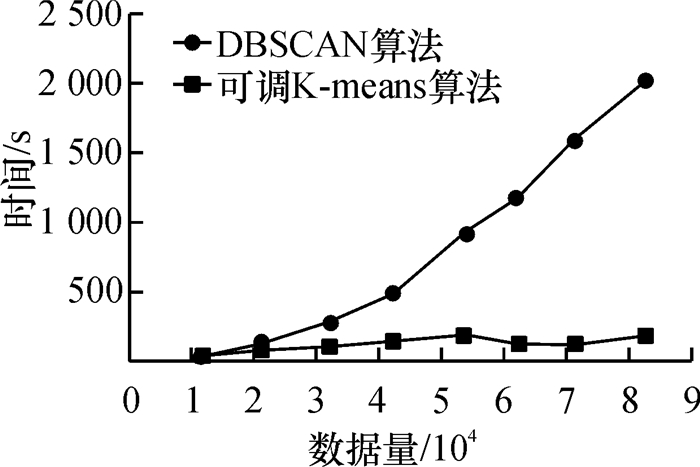
实验中分别记录了11组可调多趟K-means聚类算法和基于密度的DBSCAN [4]算法的运算时间,如图 4所示.
|
图 4 算法效率示意图 Figure 4 The diagram of the algorithm efficiency |
从图 4可以看出,由于初始值的选取有一定随机性,本文提出的可调多趟K-means聚类算法达到收敛时的迭代次数存在一定的不确定性,算法的执行时间有一定的波动.当数据量达到一定规模时,多趟K-means聚类算法的效率远远高于传统的DBSCAN算法.
由实验结果可知,通信质量好的客户数有40 869个,通信质量差的客户数有3 078个,说明当前环境下,通信质量总体情况令人满意.但是移动运营商仍需要分析通信质量差的3 078位客户与通信质量较差的2 930位客户,找出通信质量差的原因并及时进行处理,以尽量降低客户流失.
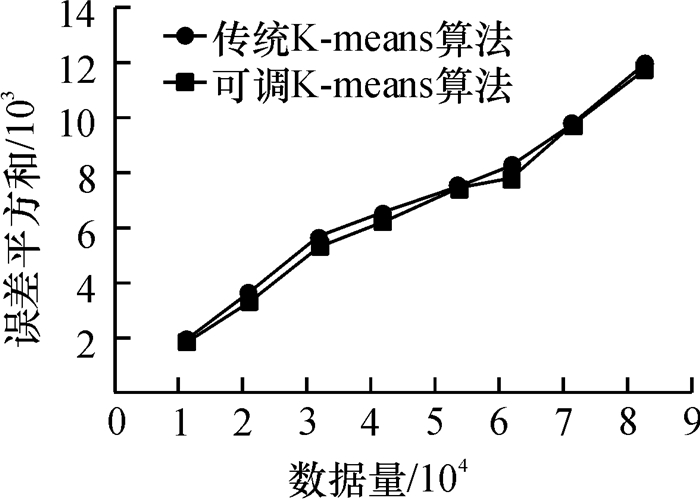
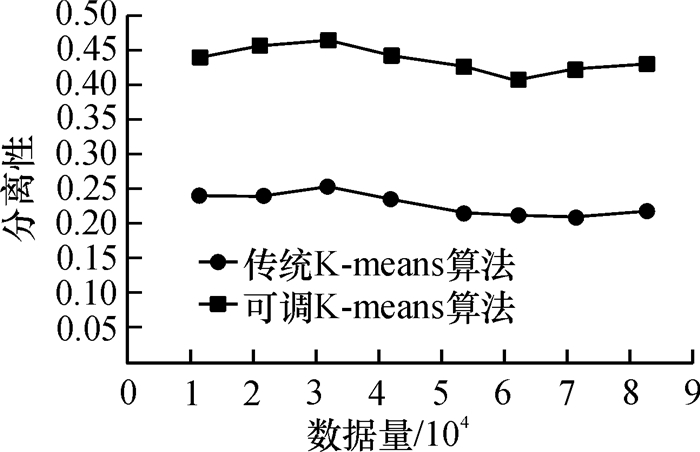
4.2 聚类效果的对比实验将传统K-means算法和本文提出的可调多趟K-means的聚类效果进行比较,从误差平方和与分离性两个评价指标进行对比,结果如图 5和图 6所示.
|
图 5 算法误差平方和示意图 Figure 5 The diagram of the error squares ofthe algorithm |
|
图 6 算法分离性示意图 Figure 6 The diagram of thealgorithmseparation |
从图 5中可以看出,本文提出的可调多趟K-means聚类算法效果在“相似性”方面略优于传统的K-means算法.由图 6可知,在“相异性”方面,可调多趟K-means聚类算法远远优于传统K-means算法.
从以上实验结果可知,本文提出的可调多趟K-means聚类算法能够有效地处理海量数据的挖掘问题,该聚类算法应用于电信领域的客户细分有效、可行.本文为电信运营商有效地细分客户提供了参考.
5 结束语K-means是目前数据挖掘中常用的聚类方法,本文针对传统K-means方法的缺点,提出了一个可调的多趟K-means聚类方法,该方法能够在保留传统K-means聚类方法优点的基础上有效地改进K-means存在的不足,并能根据实际需要分析并调整聚类结果的个数.实验表明,该算法应用于电信数据分析及其客户细分有效、可行,下一步工作将探讨本文的方法在大数据挖掘中的应用.
| [1] |
Reicheld F F, Sasser W E. Zero defections: Quality comes to services[J].
Harvard Business Review, 1990, 42(9): 105-110.
|
| [2] |
张巍, 滕少华, 彭重嘉, 等. 基于业务的移动网络用户体验协同建模方法[J].
兰州大学学报:自然科学版, 2012, 48(4): 80-84.
Zhang W, Teng S H, Peng C J, et al. Business-based cooperative modeling method for QoE of the mobile network[J]. Journal of Lanzhou University:Natural Sciences Edition, 2012, 48(4): 80-84. |
| [3] |
徐猛. 面向用户体验的多QoS约束多流程调度方法研究[D]. 济南: 山东大学计算机科学与技术学院, 2010.
http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1791821
|
| [4] |
周天圆. 智能算法在电信业务用户体验感知分析中的应用[D]. 长春: 吉林大学计算机科学与技术学院, 2011.
|
| [5] |
郑茜茜. 基于数据挖掘的客户细分研究[D]. 重庆: 重庆交通大学管理学院, 2013.
http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2302792
|
| [6] |
Han J W, Kamber M, Pei J. 数据挖掘概念与技术[M]. 北京: 机械工业出版社, 2012.
|
| [7] |
白亮. 聚类学习的理论分析与高效算法研究[D]. 山西: 山西大学计算机与信息技术学院, 2012.
http://cdmd.cnki.com.cn/Article/CDMD-10108-1012484959.htm
|
| [8] |
王扶东, 马玉芳. 基于数据挖掘的客户细分方法的研究[J].
计算机工程与应用, 2011, 47(4): 215-218.
Wang F D, Ma Y F. Research of method for customer segment based on data mining[J]. Computer Engineering and Applications, 2011, 47(4): 215-218. |
| [9] |
杜巍, 赵春荣, 黄伟建. 改进的K-means聚类算法在客户细分中的应用研究[J].
河北经贸大学学报, 2014, 35(1): 118-121.
Du W, Zhao C R, Huang W J. Application of improved K-means cluster algorithm to customer segmentation[J]. Journal of Hebei University of Economics and Business, 2014, 35(1): 118-121. |
| [10] |
Mahmud M S, Rahman M M, Akhtar M N. Improvement of K-means Clustering algorithm with better initial centroids based on weighted average[C]// 2012 7th International Conference on Electrical and Computer Engineering. Dhaka: IEEE, 2012: 647-650
|
| [11] |
王令剑, 滕少华. 聚类和时间序列分析在入侵检测中的应用[J].
计算机应用, 2010, 30(3): 699-701, 714.
Wang L J, Teng S H. Application of clustering and time-based sequence analysis in intrusion detection[J]. Journal of Computer Applications, 2010, 30(3): 699-701, 714. |
| [12] |
曹永春, 蔡正琦, 邵亚斌. 基于K-means的改进人工蜂群聚类算法[J].
计算机应用, 2014, 34(1): 204-207, 217.
Cao Y C, Cai Z Q, Shao Y B. Improved artificial bee colony clustering algorithm based on K-means[J]. Journal of Computer Applications, 2014, 34(1): 204-207, 217. DOI: 10.11772/j.issn.1001-9081.2014.01.0204. |
| [13] |
胡伟. 改进的层次K均值聚类算法[J].
计算机工程与应用, 2013, 49(2): 157-159.
Hu W. Improved hierarchical K-means clustering algorithm[J]. Computer Engineering and Applications, 2013, 49(2): 157-159. |
| [14] |
高灵渲, 张巍, 霍颖翔, 等. 改进的聚类模式过滤推荐算法[J].
江西师范大学学报, 2012, 36(1): 106-110.
Gao L X, Zhang W, Huo Y X, et al. Improved clustering filtering recommendation algorithm[J]. Journal of Jiangxi Normal University:Natural Science Edition, 2012, 36(1): 106-110. |
| [15] |
易倩, 滕少华, 张巍. 基于马氏距离的K均值聚类算法的入侵检测[J].
江西师范大学学报, 2012, 36(5): 284-287.
Yi Q, Teng S H, Zhang W. Mahalanobis distance-based K-means clustering algorithm for intrusion detection[J]. Journal of Jiangxi Normal University:Natural Science Edition, 2012, 36(5): 284-287. |
| [16] |
Teng S H, Du H L, Zhang W, et al. A cooperative network intrusion detection based on heterogeneous distance function clustering[C]//[s. l. ]: CSCWD, 2010: 140-145.
|
| [17] |
廖松有, 张继福, 刘爱琴. 利用模糊熵约束的模糊C均值聚类算法[J].
小型微型计算机系统, 2014, 35(2): 379-383.
Liao S Y, Zhang J F, Liu A Q. Fuzzy C means clustering algorithm by using fuzzy entropy constraint[J]. Journal of Chinese Computer Systems, 2014, 35(2): 379-383. |
| [18] |
卢鹏丽, 王祖东. 密度敏感的层次化聚类算法研究[J].
计算机工程与应用, 2014, 50(4): 190-195.
Lu P L, Wang Z D. Density-sensitive hierarchical clustering algorithm[J]. Computer Engineering and Applications, 2014, 50(4): 190-195. |
| [19] |
潘章明, 陈尹立. 面向大数据集的共享近邻聚类研究[J].
小型微型计算机系统, 2014, 35(1): 50-54.
Pan Z M, Chen Y L. Research on shared nearest neighbor clustering for large dataset[J]. Journal of Chinese Computer Systems, 2014, 35(1): 50-54. |
| [20] |
曾昭才. 移动统计——移动网络分析的另一宝藏[J].
移动通信, 2005(11): 93-95.
DOI: 10.3969/j.issn.1006-1010.2005.11.020. |
| [21] |
苗守野, 肖瑞. 基于MR的3G无线网络质量评估方法研究[J].
移动通信, 2011(18): 22-26.
DOI: 10.3969/j.issn.1006-1010.2011.18.005. |
 2014, Vol. 31
2014, Vol. 31