2. 广汽集团 汽车工程研究院,广东 广州 510640
2. Automotive Engineering Institute, Guangzhou Automobile Group Co.Itd, Guangzhou 510640, China
悬架系统是汽车的车架与车桥或车轮之间的一切传递力和力矩装置的总称,决定着汽车的操纵稳定性、舒适性,是现代汽车十分关键的部件之一[1-2].车轮定位参数与车轮跳动之间的关系反映了悬架运动特性的优劣[3-4].悬架杆件的布置决定了悬架运动学特性,两者之间关系的研究可以为合理设计悬架及提高汽车性能提供重要的理论及试验依据[5-6].
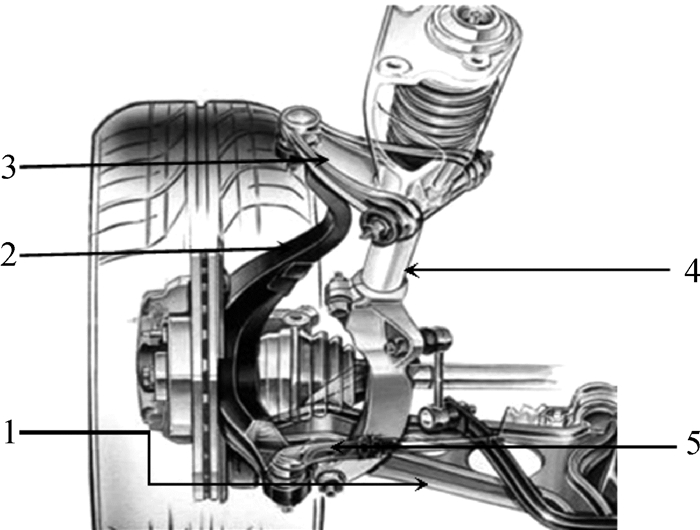
1 双叉臂前悬架系统模型建立 1.1 双叉臂悬架结构某SUV轿车双叉臂独立前悬架系统分左、右两侧对称于整车纵向平面分布.左侧悬架结构如图 1所示.该悬架系统由上、下叉臂,弹簧减振器总成,转向轴节和转向横拉杆组成.上、下叉臂内侧以橡胶衬套与副车架连接,外侧以球销与转向轴节连接;弹簧减振器总成上、下端各自以橡胶衬套分别连接车身和下叉臂;转向横拉杆内、外端分别以球销连接在转向机和转向节上;转向节通过法兰盘的制动器安装孔与制动系统连接.
|
图 1 双叉臂独立悬架系统左侧悬架结构 Figure 1 The structure of the left side of the independent double wishbone front suspension 1.下叉臂;2.转向节;3.上叉臂;4.弹簧减振器总成;5.转向横拉杆 |
在车轮上跳的过程中,对车轮定位参数的变化起主导作用的为悬架系统的几何布置以及杆件间的连接关系.而杆件自身的变形、杆件间连接的间隙、运动副内的摩擦均较小[7-8],这些因素对悬架的运动学特性影响很小.
为更清楚地研究影响悬架运动学特性的主要因素,本文对悬架模型作如下假设:(1)弹簧减振器总成简化为线性弹簧和阻尼[9];(2)各运动副内的摩擦力忽略不计;(3)上、下摆臂,转向节和转向横拉杆认为是刚性的;(4)杆件间连接的间隙不计;(5)前悬架理想对称于整车纵向平面,只分析悬架左半部分的运动学特性.
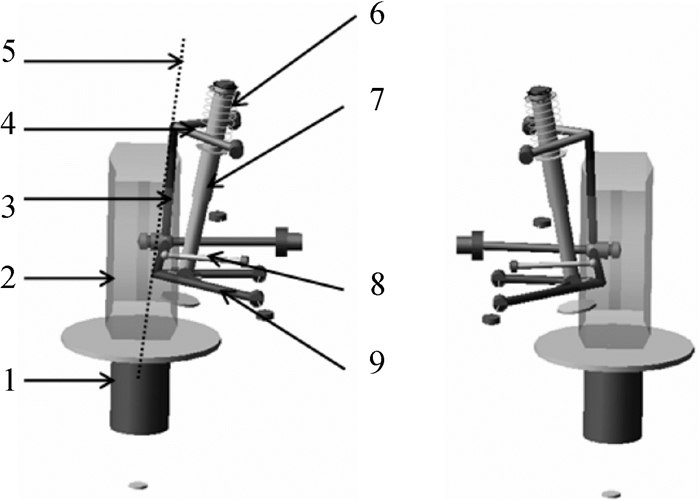
利用动力学分析软件ADAMS\Car模块,建立如图 2所示的双叉臂前悬架动力学模型.
|
图 2 双叉臂前悬架动力学模型 Figure 2 Dynamic model of the double wishbone front suspension 1.试验台;2.车轮;3.转向节;4.上叉臂;5.主销;6.弹簧;7.减振器;8.转向横拉杆;9.下叉臂. |
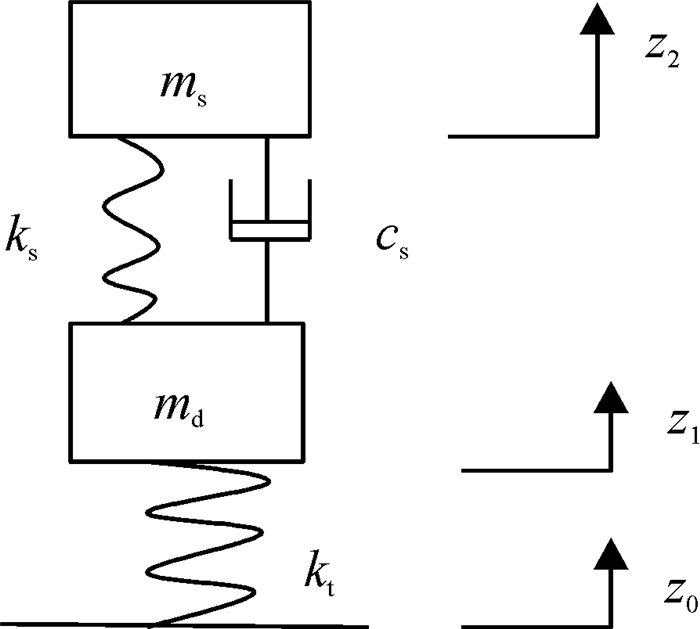
基于上述物理模型,结合车辆动力学理论,建立如图 3所示的二自由度悬架系统简化模型.
|
图 3 二自由度悬架系统简化模型 Figure 3 The simplistic model of the two-freedom suspension system |
其中,ms为悬架弹簧上端所承载的质量;md为悬架弹簧下端所承载的质量;ks为悬架刚度;kt为轮胎刚度;cs为减振器阻尼;z0、z1和z2分别为地面输入、轮胎和簧上质量的垂向跳动量.
悬架系统运动方程为[10]
| $ {m_{\text{s}}}{\mathit{\boldsymbol{\ddot z}}_2} = - {c_{\text{s}}}\left( {{{\mathit{\boldsymbol{\dot z}}}_2} - {{\mathit{\boldsymbol{\dot z}}}_1}} \right) - {k_{\text{s}}}\left( {{\mathit{\boldsymbol{z}}_2} - {\mathit{\boldsymbol{z}}_1}} \right), $ | (1) |
| $ {m_{\text{d}}}{\mathit{\boldsymbol{\ddot z}}_1} = {c_{\text{s}}}\left( {{{\mathit{\boldsymbol{\dot z}}}_2} - {{\mathit{\boldsymbol{\dot z}}}_1}} \right) - {k_{\text{t}}}\left( {{\mathit{\boldsymbol{z}}_1} - {\mathit{\boldsymbol{z}}_0}} \right) + {k_{\text{s}}}\left( {{\mathit{\boldsymbol{z}}_2}\mathit{ - }{\mathit{\boldsymbol{z}}_1}} \right). $ | (2) |
取状态变量
| $ \mathit{\boldsymbol{\dot X = AX + BY}}, $ | (3) |
| $ \mathit{\boldsymbol{Y = CX}}. $ | (4) |
其中,
| $ \begin{gathered} \mathit{\boldsymbol{A = }}\left[ {\begin{array}{*{20}{c}} 0&0&1&0 \\ 0&0&{ - 1}&1 \\ { - {k_{\text{t}}}/{m_{\text{d}}}}&{{k_{\text{s}}}/{m_{\text{d}}}}&{ - {c_{\text{s}}}/{m_{\text{d}}}}&{{c_{\text{s}}}/{m_{\text{d}}}} \\ 0&{ - {k_{\text{s}}}/{m_{\text{s}}}}&{{c_{\text{s}}}/{m_{\text{s}}}}&{ - {c_{\text{s}}}/{m_{\text{s}}}} \end{array}} \right], \hfill \\ \hfill \\ \end{gathered} $ |
| $ \mathit{\boldsymbol{B = }}{\left[ { - 1\;\;\;0\;\;\;0\;\;\;0} \right]^{\text{T}}}, $ |
| $ \mathit{\boldsymbol{C = }}\left[ {\begin{array}{*{20}{c}} 0&{{k_{\text{s}}}/{m_{\text{s}}}}&{{c_{\text{s}}}/{m_{\text{s}}}}&{ - {c_{\text{s}}}/{m_{\text{d}}}} \\ 0&1&0&0 \\ 1&0&0&0 \end{array}} \right]. $ |
该车前悬行程为-95~100 mm,故对建立好的悬架模型进行车轮下跳95 mm,上跳100 mm的平行轮跳试验.
2.1 仿真数据处理ADAMS后处理模块存在着拟合试验数据失真的缺陷,不利于悬架运动学试验与仿真数据对比.本文对悬架模型仿真后的数据和悬架试验数据进行提取,并利用软件编程,使用线性最小二乘法进行3次多项式拟合.线性最小二乘法的基本方法是,对平面上的n个点(xi,yi),寻求一个函数y=f(x), 使得yi与f(xi)的距离的平方和最小[11].该方法避免了悬架试验数据拟合失真的问题,更利于直观真实地反映悬架运动学特性.
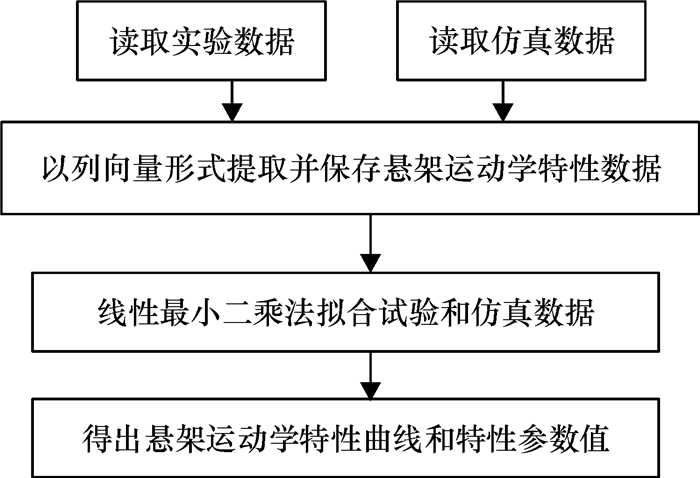
数据处理的流程如图 4所示.其中,悬架运动学特性参数是指车轮定位参数和轮距随车轮跳动时在零点的梯度值.
|
图 4 数据处理的流程图 Figure 4 Flow char of the processing of data |
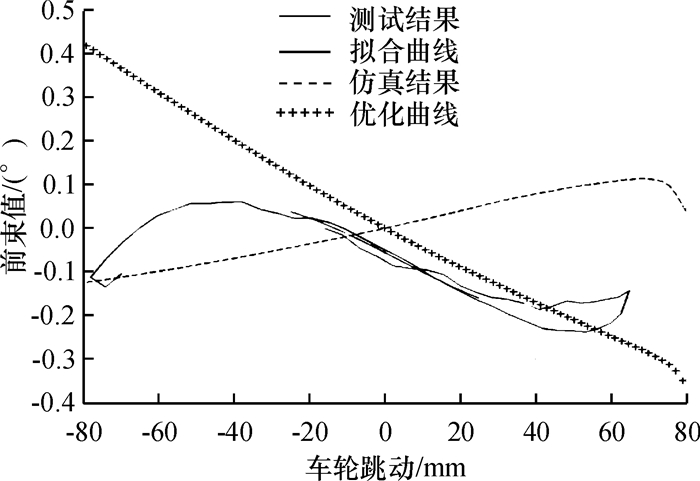
对建立的悬架模型进行平行轮跳仿真数据以及对标车试验数据处理后,得到如图 5~图 9中反映对标车试验测试结果的闭合的实线、用线性最小二乘法拟合试验数据所得的非闭合的实线和反映该双叉臂悬架仿真结果的虚线.试验结果中,前束、外倾变化数据由悬架K&C试验台测出;主销内、外倾角由四轮定位仪测得;主销纵向偏移距受仪器限制而只由仿真得出.
|
图 5 前轮前束值变化曲线 Figure 5 Toe change curve of the front wheel |
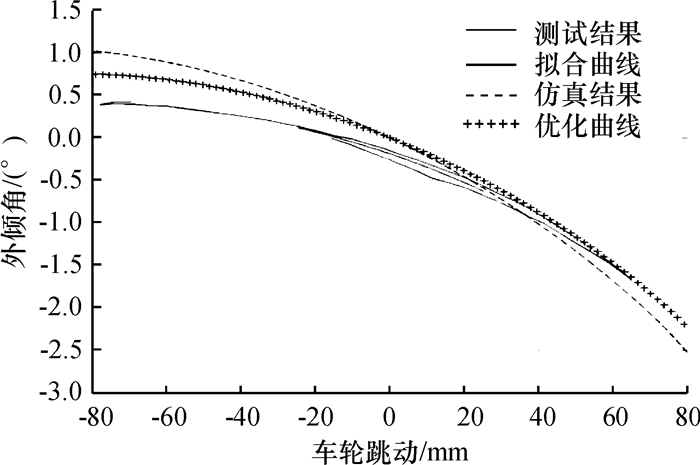
|
图 6 前轮外倾角变化曲线 Figure 6 Camber change curve of the front wheel |
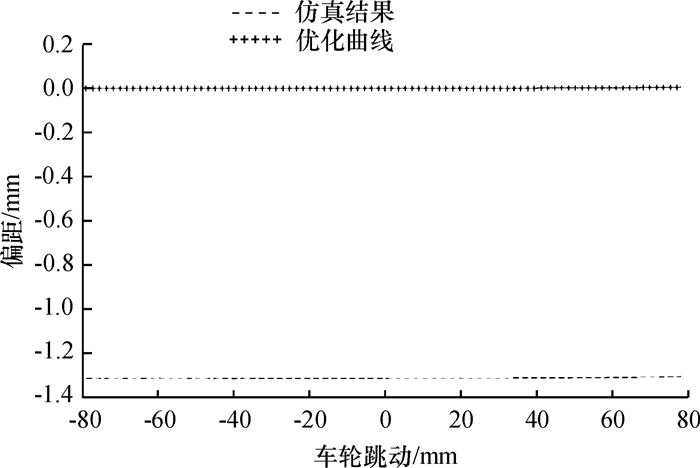
|
图 7 主销轮心纵向偏移距 Figure 7 The longitude distance between wheel center and the kingpin |
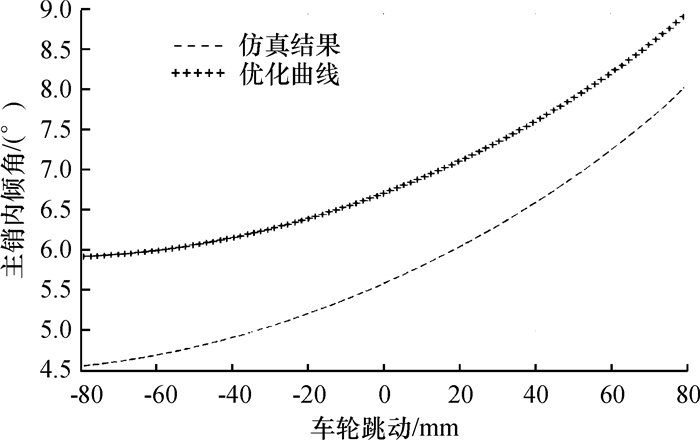
|
图 8 主销内倾角变化曲线 Figure 8 Kingpin inclination angle change curve |
|
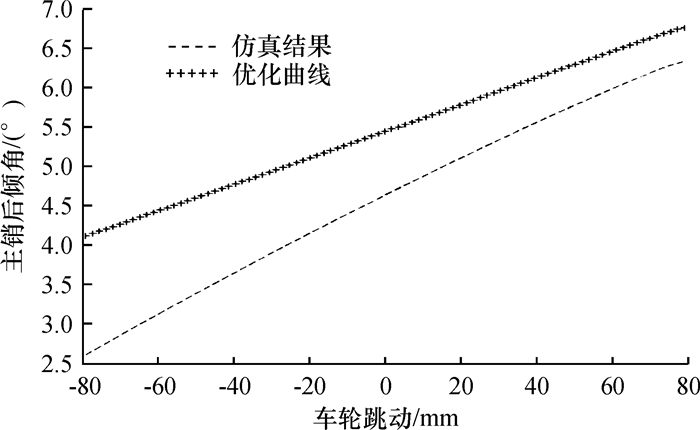
图 9 主销后倾角变化曲线 Figure 9 Caster angle change curve |
由图 5~图 9中得到对标车实验结果和本文悬架模型的仿真结果,如表 1中试验值与仿真值所示.
| 表 1 试验与仿真结果对比 Table 1 Comparisons between the results of the experiment and simulation |
为使汽车有不足转向特性,一般希望车轮上跳时,车轮有负前束和负外倾变化趋势[12-13].从汽车操稳性考虑,一般希望主销内倾角、主销后倾角均有正的变化趋势,主销轮心纵向偏移距为零[14-15].由图 5~图 9及表 1,以对标车试验参数为参考,可知该悬架主销内倾角、主销后倾角变化趋势合理.前轮有正前束变化趋势,而且外倾变化梯度过大,主销轮心纵向偏移距非零,均需进一步优化.
3 硬点灵敏度分析与优化 3.1 硬点灵敏度分析悬架的硬点布置决定了悬架杆件的布置形式,从而决定了悬架的运动学特性[15].在只考虑该悬架系统左半部分时,该悬架系统硬点包括上、下叉臂的6个硬点、转向横拉杆的2个硬点、弹簧减振器总成3个硬点、轮心处1个硬点,共12个硬点.因弹簧减振器总成本身自由度为零,不会对悬架系统运动学特性产生影响,而轮心位置在设计之初已定义完成,故本文以前轮前束角、外倾角、主销纵向偏移距、主销内倾角和主销后倾角等作为5个设计目标,选择该悬架除弹簧减振器总成上的3个硬点和轮心位置的1个硬点外的8个硬点,以此8个硬点的 x、y、z 3个坐标值作为设计变量,对这24个设计变量做两水平试验的灵敏度分析,得到各设计变量对所选设计目标的灵敏度.本文以前束和外倾为例,列出对各个设计目标影响最大的前5个设计变量,如表 2所示,并参照该灵敏度分析结果优化该悬架硬点.
| 表 2 灵敏度分析结果 Table 2 Results of the sensibility analysis |
根据灵敏度分析结果,以及上述2.2节的分析,列出如表 1中目标值所示的待优化悬架的设计目标.针对各个设计目标,尽量避免耦合因素的影响,分别选择与之相对应较灵敏的设计变量进行调整,依次优化上述设定的5个设计目标.经过多次反复迭代优化后,得到如图 5~图 9中+号线所示的优化后的悬架运动学特性曲线和表 1中优化值所示的优化后的悬架运动学特性值.优化后的硬点坐标变动情况如表 3所示.
| 表 3 硬点坐标变动 Table 3 Change of the hardpoints' coordinates |
在优化的过程中可发现,上、下叉臂外点的布置决定了主销在空间的布置.转向横拉杆内外点的高度差以及杆长对车轮前束变化影响很大.这是由于在车轮上跳时,转向横拉杆外点绕内点的转动,带动车轮的垂向转动所致的.当悬架整体结构确定后,微小的硬点调整对车轮外倾变化影响很小.相对而言,下叉臂内外点的高度差对外倾变化影响较大.这是车轮上跳时,下叉臂外点绕内点摆动,带动车轮的纵向摆动造成的.
4 结束语本文旨在提供一种悬架优化的方法,从图 5~图 9及表 1可以看出,经优化后的悬架前束、外倾值和主销倾角值满足了设计目标的要求,前束、外倾的变化曲线与对标车试验结果曲线更逼近.这说明本文所建立的悬架动力学模型是正确的,实验数据的处理方法是合理的,悬架硬点优化的方法是恰当的.
| [1] |
周长城.
汽车液压筒式减振器设计及理论[M]. 北京: 北京大学出版社, 2012.
|
| [2] |
Wu Y M, Ruan M Q. The application of virtual pro- totype-technology in optimization of suspension kinematical performance[J].
Machinery Design & manufacture, 2007, 13(11): 175-177.
|
| [3] |
王爽. 某微车悬架K & C特性研究及其对整车操纵稳定性的影响[D]. 长春: 吉林大学汽车工程学院, 2008.
|
| [4] |
刘昆, 彭美春, 林怡青, 等. 基于ANSYS Workbench鼓式制动器冲焊蹄的有限元分析[J].
广东工业大学学报, 2013, 30(1): 92-96.
Liu K, Peng M C, Lin Y Q, et al. Finite element analysis of drum brake stamping-welding shoes based on ANSYS workbench[J]. Journal of Guangdong University of Technology, 2013, 30(1): 92-96. |
| [5] |
张斌彧, 熊锐, 陈礼. 基于拉格朗日的汽车动力总成悬置系统振动分析[J].
广东工业大学学报, 2011, 28(1): 41-44.
Zhang B Y, Xiong R, Chen L. The modeling of automobile powertrain mounting system and vibration analysis by lagrange[J]. Journal of Guangdong University of Technology, 2011, 28(1): 41-44. |
| [6] |
马涛锋. 前悬架参数变化对整车操纵稳定性的影响[D]. 镇江: 江苏大学汽车与交通工程学院, 2005.
|
| [7] |
米奇克.
汽车动力学[M]. 北京: 清华大学出版社, 2009.
|
| [8] |
约森·赖姆佩尔.
悬架元件及底盘力学[M]. 长春: 吉林科学技术出版社, 1992.
|
| [9] |
Verma M K, Gillespie T D. Roll dynamics of commercial vehiles[J].
Vehicle Systerm Dynamics, 1980(9): 1-17.
|
| [10] |
Xiao L J, Li R F. Vehicle chassis simulation and su spension system performance optimization based on AD- AMS[J].
Journal of System Simulation, 2006, 18(7): 2007-2010.
|
| [11] |
王振友, 郑少杰, 何远才, 等. 基于PCA方法的PET图像多示踪剂分离[J].
广东工业大学学报, 2013, 30(2): 42-46.
Wang Z Y, Zheng S J, He Y C, et al. The application of principle component analysis to the separa- tion of multiple tracers in PET images[J]. Journal of Guangdong University of Technology, 2013, 30(2): 42-46. |
| [12] |
倪佑民.
汽车方向稳定性基本原理[M]. 北京: 清华大学出版社, 1978.
|
| [13] |
安部正人.
汽车的运动和操纵[M]. 北京: 机械工业出版社, 1998.
|
| [14] |
Jomsen Reimpell HelutStoll. Automotive Chasis:Engineeri-ng Principles[M]. London: Arnold, 1996.
|
| [15] |
王行, 阳林, 彭仁杰, 等. 基于ADAMS的FSAE赛车前悬架优化设计[J].
广东工业大学学报, 2013, 30(3): 105-108.
Wang H, Yang L, Peng R J, et al. Optimization of a FSAE Racing car's front suspension based on ADAMS[J]. Journal of Guangdong University of Technology, 2013, 30(3): 105-108. |
 2014, Vol. 31
2014, Vol. 31