大气延迟是雷达干涉测量(Interferometric Synthetic Aperture Radar, InSAR)中最主要的一种误差源[1-3].目前,改正InSAR大气延迟误差的方法主要有:(1)基于外部观测数据,如GPS[4-5]、MERIS[6]、MODIS[7]、气象模型等[8-10];(2)采用多幅干涉图进行叠加[11]或时间序列分析[12-13].这些方法均在不同的案例研究中体现了它们对于提高InSAR精度的优越性.然而,第一类方法较大地依赖于外部数据与InSAR在时间和空间分辨率上的一致性,后者则需要多期InSAR观测资料,而且时间序列分析还依赖于数据处理人员的主观判断,缺少客观衡量指标.正是由于这些方法都存在缺陷,导致目前没有一个完善的InSAR大气延迟误差改正方法.
鉴于目前大部分地区没有密集的GPS测站,而其他遥感手段在空间和时间分辨率上与InSAR卫星差别较大,近几年采用气象模型改正InSAR大气延迟误差似乎正成为一种主流的方法和趋势,受到InSAR研究人员的广泛关注[8-10].
然而,由于气象参数同样存在获取的时间、空间分辨率与InSAR不一致的问题,很多研究者发现气象模型得到的延迟并不一定十分可靠[14].本文采用青藏高原中部多幅雷达影像和欧洲中尺度天气预报中心(ECMWF)气象模型,分析基于该模型改正InSAR大气延迟误差的可靠性.
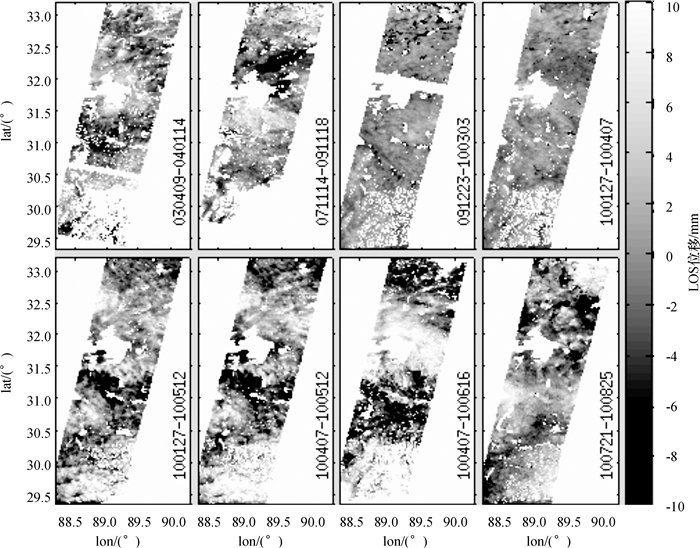
1 实验区域与数据本文采用欧洲空间局ENVISAT卫星采集的第219轨道雷达影像数据,研究区域为青藏高原中部北纬28°到35°之间.采用Caltech/JPL联合开发的ROI_PAC软件[15]处理12景雷达影像,共获得了8幅干涉图,如图 1所示.根据雷达影像获取的时间,本文选取欧洲中尺度天气预报中心提供的相应气象参数,包括温度、气压、湿度等参数,并结合研究区域的数字高程模型,采用开源程序PyAPS[10]计算不同高度的天顶向大气延迟,然后投影到InSAR视距(line-of-sight,LOS)方向,从而获得每个雷达影像历元所对应的ECMWF模型大气延迟.最后依据InSAR像对的日期,选取相应的两幅大气延迟图像求差,最终获得与InSAR干涉图相对应的大气延迟误差改正量,如图 2所示.将原始干涉图减去大气延迟误差,得到改正后的干涉图,如图 3所示.
|
图 1 大气延迟误差改正前的干涉图 Figure 1 Interferograms before atmospheric delay correction |
|
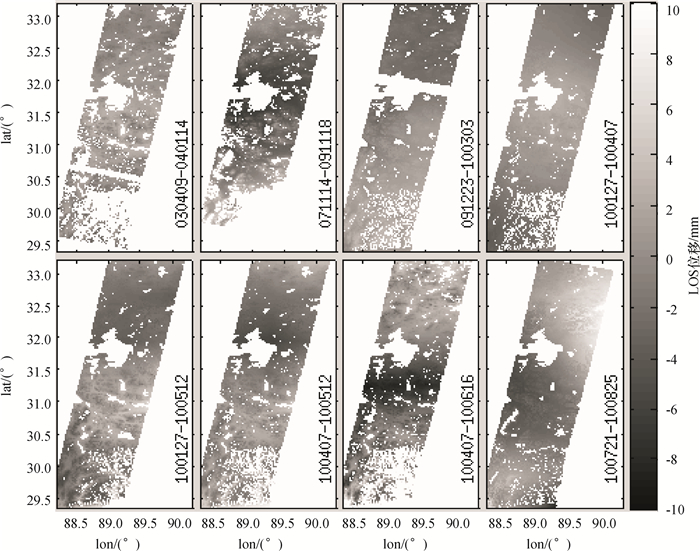
图 2 基于ECMWF模型计算的大气延迟量 Figure 2 Atmospheric delay from ECMWF model |
|
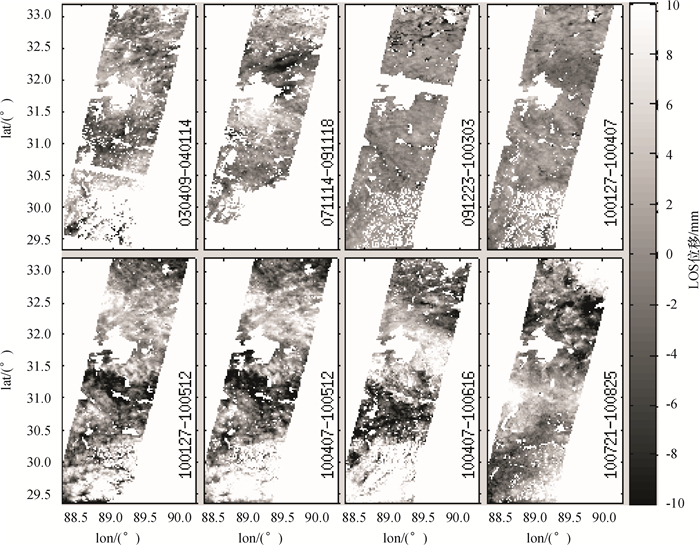
图 3 大气延迟误差改正后的干涉图 Figure 3 Interferograms after removing atmospheric delay errors |
本文采用指数函数来估计大气延迟误差的大小及其空间尺度特征[16].该模型已被广泛用于建立InSAR大气延迟误差的随机模型,其具体表达式为
| $ c = {\sigma ^2}{e^{ - d/\alpha }}, $ | (1) |
其中c表示干涉图中任意两个像素之间的协方差,σ2表示干涉图的方差,通常用来衡量干涉图中大气延迟误差的大小,d为干涉图中两像素之间的距离,α为大气延迟的尺度因子,通常用来表示大气延迟误差的空间相关尺度.
在方程(1)中,对于每幅干涉图,可以利用各个像素的相位值计算出像素之间的协方差c以及像素之间的距离d.据此,采用最小二乘准则,能够反演出每幅干涉图的方差以及大气延迟的尺度因子.为了衡量大气延迟误差的改正效果,分别计算采用ECMWF模型改正前后干涉图的方差,其结果如表 1所示.
| 表 1 ECMWF大气延迟误差改正前后方差统计表 Table 1 Variances with/without atmospheric delay corrections |
表 1中数据说明,本文计算的8幅干涉图中有5幅没有改进效果,另外3幅干涉图的方差比改正前稍有减小.经过大气延迟误差改正后,全部干涉图的方差均值反而更大.因此,总体来说ECMWF模型对于本文采用的数据没有起到改进作用.究其原因,认为主要有3点:
(1) ECMWF气象数据空间分辨率较低.湿延迟误差在空间域变化较快,一般其变化尺度可能为1 km甚至更小.本文使用的InSAR图像分辨率为90 m,而ECMWF气象数据分辨率为70 km,两者相差太大导致该模型难以改正小尺度的湿延迟误差.由图 2也可以看出,ECMWF模型计算的大气延迟量在空间上非常平滑,无法反映大气延迟的局部细节变化.
(2) ECMWF气象参数的获取时间与雷达影像不一致.InSAR卫星采集数据的时间是早上4点,而与之最接近的ECMWF气象数据的采集时间是早上6点,存在两个小时的滞后.众所周知,高原地区早晚温差大,尤其是在日出前后几小时,气象条件可能会产生明显的变化,从而导致依据气象模型计算的大气延迟具有较大的误差.此外,由于气象遥感卫星获取的数据普遍存在时间分辨率较低的问题,因此,即使在今后也很难获得在时间上与InSAR数据匹配的气象参数.不过,由于大多数InSAR卫星在某一地区获取数据的时刻基本是固定的,如果气象卫星采集数据的时刻和当地的InSAR数据正好同步,则有望提高气象模型改正InSAR大气延迟误差的精度.实际上,在Envisat卫星上配备的MERIS仪器正是因为始终能够获得与Envisat雷达卫星同步的气象参数,所以采用MERIS观测数据能够较好地改正InSAR大气延迟误差[6].
(3) 研究区域地形起伏不太大.使用ECMWF模型计算的大气延迟,最早是用于研究昆仑山地区的大气延迟改正[10],该地区地形起伏为2.8~6.0 km,干延迟影响比较大.与湿延迟不同,干延迟表现为大尺度特征,因此,采用分辨率不高的ECMWF模型改正能够获得较好的结果.但是本研究区域地形起伏只有1 km左右,以小尺度的湿延迟为主,干延迟影响不大,因此,同样使用ECMWF模型改正但是效果却较差.
3 结束语本文采用西藏中部8幅干涉图检验ECMWF气象模型改正InSAR大气延迟误差的效果.实验结果表明,该模型无法很好地改正大气延迟误差.主要原因在于ECMWF气象参数与InSAR数据的时间和空间分辨率不同、研究区域的地形起伏不太大.鉴于此,建议谨慎采用该模型改正大气延迟误差.
此外,在GPS等空间大地测量研究中已经证明,气象模型不能很好地改正大气中的湿延迟分量.InSAR与GPS等空间大地测量中的大气延迟误差属性基本相同,因此,InSAR大气延迟误差难题的最终解决方法需要更多地依赖于InSAR数据本身(比如正兴起的InSAR卫星星座工作模式),而不是寄希望于获得更高分辨率的气象模型参数.
| [1] |
Goldstein R M. Atmospheric limitations to repeat-track radar interferometry[J].
Geophys Res Lett, 1995, 22(18): 2517-2520.
DOI: 10.1029/95GL02475. |
| [2] |
Zebker H A, Rosen P A, Hensley S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps[J].
J Geophys Res, 1997, 102(B4): 7547-7563.
DOI: 10.1029/96JB03804. |
| [3] |
Hanssen R F. Radar Interferometry: Data Interpretation and Error Analysis[M]. Dordrecht: Kluwer Academic Publishers, 2001: 130-153.
|
| [4] |
Xu C, Wang H, Ge L, et al. InSAR tropospheric delay mitigation by GPS observations: A case study in Tokyo area[J].
J Atmos Sol-Terr Phy, 2006, 68(6): 629-638.
DOI: 10.1016/j.jastp.2005.11.010. |
| [5] |
Li Z H, Fielding E J, Cross P, et al. Interferometric synthetic aperture radar atmospheric correction: GPS topography-dependent turbulence model[J].
J Geophys Res, 2006, 111(B02404).
DOI: 10.1029/2005JB003711. |
| [6] |
Li Z H, Fielding E J, Cross P, et al. Interferometric synthetic aperture radar atmospheric correction: medium resolution imaging spectrometer and advanced synthetic aperture radar integration[J].
Geophys Res Lett, 2006, 33(L06816).
DOI: 10.1029/2005GL025299. |
| [7] |
Li Z H, Muller J P, Cross P. Interferometric synthetic aperture radar InSAR atmospheric correction: GPS, Moderate Resolution Imaging Spectroradiometer (MODIS), and InSAR integration[J].
J Geophys Res, 2005, 110(B03410).
DOI: 10.1029/2004JB003446. |
| [8] |
Wadge G, Webley P W, James I N, et al. Atmospheric models, GPS and InSAR measurements of the tropospheric water vapour field over Mount Etna[J].
Geophys Res Lett, 2002, 29(19).
DOI: 10.1029/2002GL015159. |
| [9] |
Puyssegur B, Michel R, Avouac J P. Tropospheric phase delay in interferometric synthetic aperture radar estimated from meteorological model and multispectral imagery[J].
J Geophys Res, 2007, 112(B05419).
DOI: 10.1029/2006JB004352. |
| [10] |
Jolivet R, Grandin R, Lasserre C, et al. Systematic InSAR tropospheric phase delay corrections from global meteorological reanalysis data[J].
Geophys Res Lett, 2011, 38(L17311).
DOI: 10.1029/2011GL048757. |
| [11] |
Wright T, Parsons B, Fielding E. Measurement of interseismic strain accumulation across the North Anatolian Fault by satellite radar interferometry[J].
Geophys Res Lett, 2001, 28(10): 2117-2120.
DOI: 10.1029/2000GL012850. |
| [12] |
Ferretti A, Prati C, Rocca F. Permanent scatterers in SAR interferometry[J].
IEEE T Geosci Remote Sens, 2001, 39(1): 8-20.
|
| [13] |
Berardino P, Fornaro G, Lanari R, et al. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms[J].
IEEE Trans Geosci Remote, 2002, 40(11): 2375-2383.
DOI: 10.1109/TGRS.2002.803792. |
| [14] |
Garthwaite M C, Wang H, Wright T J. Broadscale interseismic deformation and fault slip rates in the central Tibetan Plateau observed using InSAR[J].
J Geophys Res, 2013, 118(9): 5071-5083.
DOI: 10.1002/jgrb.50348. |
| [15] |
Rosen P A, Hensley S, Peltzer G, et al. Updated repeat orbit interferometry package released[J].
Eos Trans AGU, 2004, 85(5): 47.
|
| [16] |
Parsons B, Wright T, Rowe P, et al. The 1994 Sefidabeh (eastern Iran) earthquake revisited: new evidence from satellite radar interferometry and carbonate dating about the growth of an active fold above a blind thrust fault[J].
Geophys J Int, 2006, 164(12): 202-217.
|
 2014, Vol. 31
2014, Vol. 31