漆包机是漆包线的生产设备,漆包线是在裸露的铜线(或铝线)外面包裹上一层聚酯漆,经炉膛烘烤、蒸发和固化后形成绝缘的产品.漆包线应用广泛,各种各样的感应线圈、电机绕组、变压器等多种电器设备都有大量应用.目前国际国内市场上使用的漆包机设备普遍存在较高耗能、环保、工艺优化和控制优化等问题,例如漆包线在烘烤过程中,炉膛温度高,需要消耗大量的电力能源.因此应用模糊控制对温度进行有效控制不但节约了资源也提高了效益[1].漆包机烘炉是典型的时滞、多变量,强耦合的非线性时变系统,应用传统的控制方法对漆包机烘炉温度的控制较难达到满意的效果.本文根据漆包机烘炉的特点,在复杂系统的研究中,提出参数自整定模糊PID控制算法及控制器设计[2].运用常规PID的齐格勒-尼可尔斯整定方法与模糊控制相结合,依据系统偏差值和偏差的变化率作为模糊控制器的输入,经过模糊推理,不断修正系统Kp,Ki和Kd的参数,使模糊PID控制系统保持在最佳的整定状态,对漆包机烘炉的温度控制达到满意的控制效果,降低原有控制的超调量,减少设备的电能能耗.从仿真结果可见,系统具有良好的稳定性和可靠性,控制精度明显提高,满足控制要求.
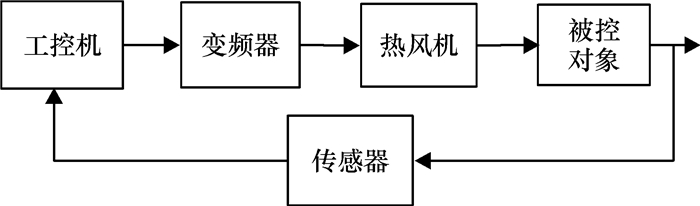
1 系统结构与PID控制原理 1.1 系统结构模型控制系统的模型结构由组态监控站[3](主站),采用RABBIT微机控制器和液晶触摸屏操作方式替代传统温控仪表,利用可编程序逻辑控制器和一批外围电器及电路,使用RS485与热电偶和变频器连接.漆包机为典型的复杂控制系统,为时变的多变量非线性系统,因此利用模糊控制理论知识结合常规PID控制算法,对系统的各个输入量进行参数的在线自整定模糊控制.其结构图如图 1所示.
|
图 1 控制系统结构模型 Figure 1 The structure model of the control system |
在控制系统中,最常用的是PID控制,其原理框图见图 2.

|
图 2 常规PID控制器原理图 Figure 2 The principle diagram of the conventional PID controller |
PID控制器是一种比例、积分、微分并联控制器.它是最广泛应用的一种控制器[4].PID控制器的数学模型可以用式(1)表示[5].
| $ u\left( t \right) = {K_{\text{p}}}\left[ {e\left( t \right) + \frac{1}{{{T_{\text{i}}}}}\int {e\left( t \right){\text{d}}\mathit{t + }{\mathit{T}_{\text{d}}}\frac{{{\text{d}}\mathit{e}\left( t \right)}}{{{\text{d}}\mathit{t}}}} } \right], $ | (1) |
其中, u(t)为控制器的输出,e(t)为误差信号(给定值和被测定值的差),Kp为比例系数, Ti为积分时间, Td为微分时间.
在工业控制中,能通过解析法和实验的方法建立起对象的数学模型.并可运用校正的方法确定PID控制器的相关参数.对于比较复杂的对象,难以求得精确数学模型,应用齐格勒-尼克尔斯法则来调整PID控制器的参数[6],显得更实用更方便.例如漆包机烘炉传递函数为:G(s)=40/s(s+2)(s+8),通过齐格勒-尼可尔斯法计算可得:比例增益Kc=4,其振荡频率为ω=4,周期Tc=2π/ω=1.5 s并查法则表(表 1)可确定PID控制器的参数为Kp=2.4,Ti=0.75 s,Td=0.19 s.
| 表 1 Z-N法则表 Table 1 Z-N Rule table |
在工程实现中通常利用近似的数学模型来代替公式(1),可表示为
| $ u\left( t \right) = {K_{\text{p}}}e\left( t \right) + {K_{\text{i}}}\sum\limits_{t = 0}^k {e\left( t \right) + {K_{\text{d}}}\left[ {e\left( t \right) - e\left( {t - 1} \right)} \right]} , $ | (2) |
其中Kp、Ki、Kd分别为比例、积分、微分系数(T为采样时间)
| $ {K_{\text{i}}} = {K_{\text{p}}}T\omega /\pi {\text{ = }}{\mathit{K}_{\text{p}}}T/{T_{\text{i}}}, $ | (3) |
| $ {K_{\text{d}}} = {K_{\text{p}}}\pi /\left( {4\omega T} \right){\text{ = }}{\mathit{K}_{\text{p}}}{T_{\text{d}}}/T. $ | (4) |
由以上方法计算可得到PID控制器的初值Kp0、Ki0和Kd0,经过模糊推理,求得初值的修正值,最终PID控制参数Kp、Ki和Kd的获取可详见第2节反模糊化.
根据系统的稳定性、响应速度和超调量等性能分析,Kp、Ki和Kd的作用[7]归纳如下:
(1) 比例部分:当出现偏差时,控制效果由比例系数Kp决定,Kp曾大,缩短了过渡过程,其稳态误差也减小;但过大的Kp值,将影响超调量,容易产生振荡,偏离预定值,导致动态性能变差,应选择适当的比例系数Kp.
(2) 积分部分:偏差的积累,其作用是消除系统的稳态误差.大的Ki,消除系统静态误差快,但过大的Ki使得响应初期出现积分饱和,随后产生超调较大.而过小的Ki又难以消除静态误差,影响调节精度.
(3) 微分部分:微分控制能提前预判出误差的变化趋势,增大微分控制作用可减小超调量,克服振荡,提高系统的稳定性,过大的Kd使响应提前制动,延长了调节的时间,而且使系统抑制干扰的能力降低.
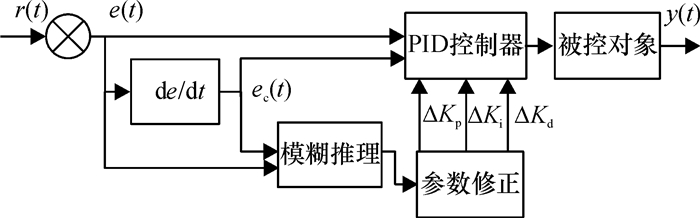
2 模糊PID控制器设计由上所述,在常规PID基础上,参数自整定模糊PID控制器的控制原理如图 3所示,控制器为两输入(误差e和误差变化量ec),3输出(Kp,Ki,Kd).模糊控制器对Kp、Ki、Kd进行在线自整定.不断满足变化的e和ec,使系统响应具有最佳的动态特性[8].
|
图 3 参数自整定模糊PID控制系统结构 Figure 3 Structure of the parameter self-setting fuzzy PID control system |
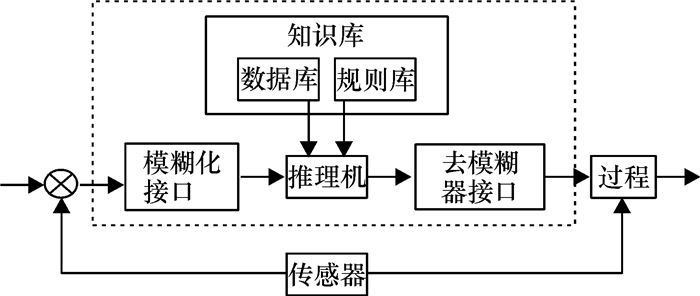
模糊控制器结构如图 4所示,要对对象进行控制,必须先对输入量做模糊化,在输出端做反模糊化.在模糊化过程中,将误差e和误差变化量ec各分成7档,以代号:-3,-2,-1,0,+1,+2,+3表示.由此的误差e和误差变化量ec的论域为X={-3,-2,-1,0,+1,+2,+3}, 误差在论域中有7个语言取值,即模糊子集为{NB, NM, NS, ZO, PS, PM, PB},分别为{负小,负中,负大,零,正小,正中,正大}.同样ΔKp,ΔKi,ΔKd也分为{NB, NM, NS, ZO, PS, PM, PB}.
|
图 4 模糊控制的基本结构 Figure 4 The basic structure of fuzzy control |
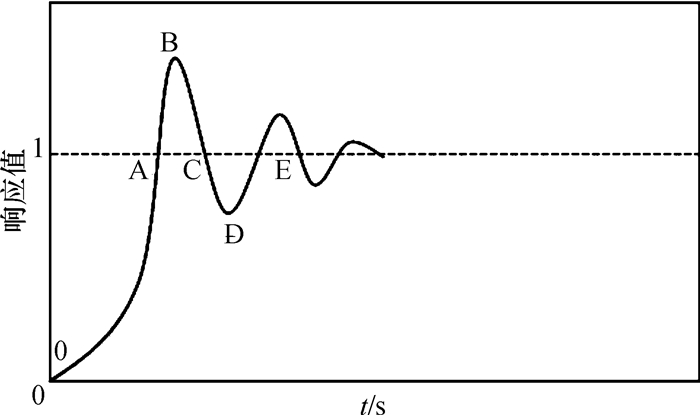
控制器需要按照一定的规则确定待修改参数的隶属范围.规则的制定可从系统的阶跃响应曲线分析得到.模糊PID的系统阶跃响应曲线如图 5可分为5区段OA~DE,响应曲线产生振荡,应该充分考虑各方面的因素,包括系统的响应速度、稳定性、超调量以及过度时间[9].由设定值减去当前值可知曲线OA段e为正值,ec为负值,曲线各区段的e和ec变化规律可见表 2.
|
图 5 系统的阶跃响应 Figure 5 System step response |
| 表 2 e×ec阶跃响应表 Table 2 e×ec step response table |
从系统的阶跃响应曲线进行分析:(1)当误差e较大时,为使误差绝对值减小,不考虑ec,应增大Kp,防止超调取为零,同时取较小Kd降低干扰.(2)当e×ec符号为“-”(负)时,误差绝对值|e|较大,取中等的Kp、较小的Ki和中等的Kd,其动态响应曲线最佳; 误差绝对值|e|较小,取较小的Kp、较大的Ki和较小的Kd,消除振荡,提高稳态特性.(3)当e×ec符号为“+”(正)时,误差绝对值|e|较大,取较大的Kp、较小的Ki和中等的Kd,其动态响应曲线最佳; 误差绝对值|e|较小,取中等的Kp、较大的Ki和较小的Kd,提高稳态特性[10].
按模糊PID控制规则根据控制器输入误差e和误差变化量ec可得出参数ΔKp,ΔKi,ΔKd的调整规则如表 3所示.其控制的条件语句共49条分别为
| 表 3 ΔKp/ΔKi/ΔKd模糊规则表1) Table 3 ΔKp/ΔKi/ΔKd fuzzy rule table |
If e=NB and ec=NB, then ΔKp=PB,ΔKi=NB,ΔKd=PS;
If e=NM and ec=NB, then ΔKp=PB,ΔKi=NB,ΔKd=PS;
If e=NS and ec=NB, then ΔKp=PM,ΔKi=NB,ΔKd=ZO;
……
……
If e=PB and ec=PB, then ΔKp=NB,ΔKi=PB,ΔKd=PS.
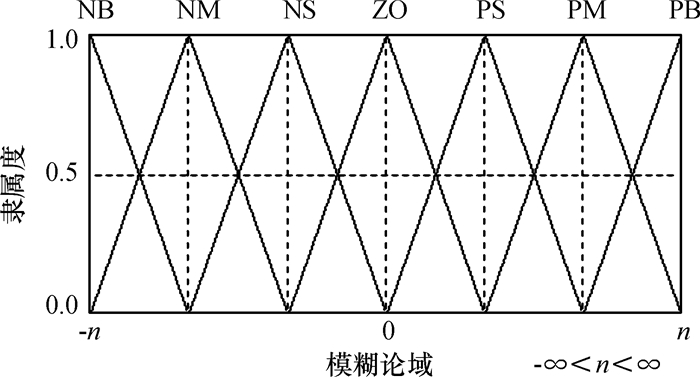
2.3 隶属函数隶属函数有三角隶属度函数、高斯函数、梯形隶属函数等等,不管采用何种隶属函数,都必须确保对输入论域的完全覆盖,同时,语言变量隶属函数之间要有适当的重叠部分[11].本文选择三角隶属度函数.e、ec、ΔKp、ΔKi、ΔKd的隶属度如图 6所示,图中模糊论域取值为[-n n], 根据参数e、ec、ΔKp、ΔKi、ΔKd分别取不同的n值.三角隶属函数其数学描述见式(5)(式中b=(a+c)/2), 其曲线如图 6所示为三角型,其中a、c为三角形斜边的两个顶点的横坐标值.
|
图 6 e,ec,ΔKp,ΔKi,ΔKd隶属度函数图 Figure 6 e, ec, ΔKp, ΔKi, ΔKd membership function diagram |
| $ {u_A}\left( x \right)\left\{ {\begin{array}{*{20}{l}} {\frac{{x - a}}{{b - a}}\;\;\;\;\;\left( {a \leqslant x \leqslant b} \right), } \\ {\frac{{x - c}}{{b - c}}\;\;\;\;\;\left( {b < x \leqslant c} \right). \;} \end{array}} \right. $ | (5) |
反模糊化,也叫做去模糊化.模糊化是模糊器将论域U上的确定值u变换为论域U上的模糊集合,模糊推理机根据规则库按一定的推理机制得出V的模糊论域集合,去模糊器将论域V上的模糊集合转为确定值v.简单地说,当推理机根据e和ec的模糊论域按规则库推理确定ΔKp在其模糊论域中为PM时,若PM(隶属度/论域值)={0/-6,0/-4,0/-2,0/0,0/2,1/4,0/6},按最大隶属度法,ΔKp=4.反模糊控制器的输出是个确定值,计算出这个确定值有多种方法,常用的有最大值法和加权平均法[12],此外还有中位数判决法.本文选用重心法,重心法又称加权平均法,即论域中的每个元素与其各自的隶属值相乘得到积Zi(i=1, 2, 3, …, L)之后求Zi的和Mc,再计算各个元素隶属度值的和Uc,然后求得平均值Z0=Mc/Uc.最后由语言变量与论域Z的赋值表查出论域元素Z0对应的精确量作为加到被控过程上的控制量[13].控制器按以上方法求得修正参数ΔKp、ΔKi、ΔKd.修正控制参数[14]由以下公式表示(式中Kp0、Ki0、Kd0分别为初值):
| $ {K_{\text{P}}} = {K_{{\text{d0}}}} + \Delta {K_{\text{P}}}, $ | (6) |
| $ {K_{\text{i}}} = {K_{{\text{i0}}}} + \Delta {K_{\text{i}}}, $ | (7) |
| $ {K_{\text{d}}} = {K_{{\text{d0}}}} + \Delta {K_{\text{d}}}. $ | (8) |
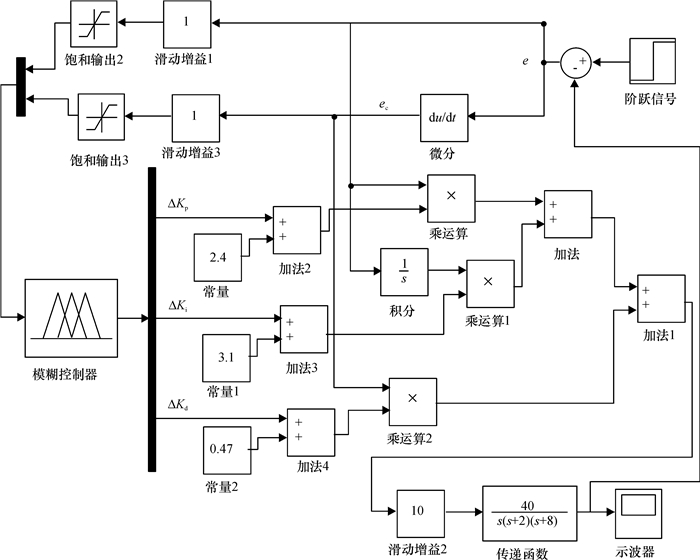
在Matlab的Simulink环境下按照模糊PID控制系统原理设计控制器[15].在Matlab的命令窗口中输入“Fuzzy”,随即弹出模糊规则编辑窗口,对规则编辑为两输入(e, ec)3输出(ΔKp,ΔKi,ΔKd),并按表 4编辑各个参数变量.其仿真程序框图如图 7所示.
| 表 4 各参数论域 Table 4 Parameters theory field |
|
图 7 仿真框图 Figure 7 The simulation diagram |
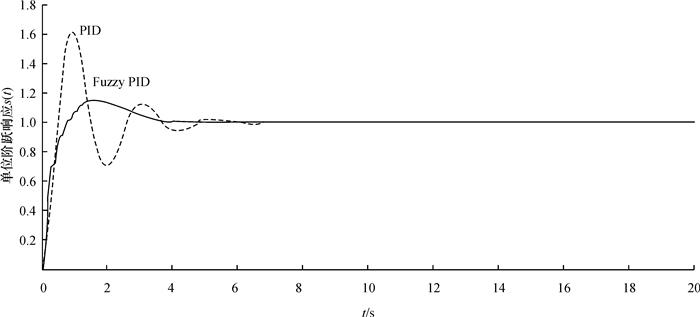
本文仿真对象是带有积分环节其数学模型传递函数为G(s)=40/s(s+2)(s+8),模糊化因子Ke=1,
|
图 8 仿真曲线图 Figure 8 The simulation curve |
针对漆包机烘炉的温度控制系统需求,本文提出了参数自整定模糊PID控制,运用常规PID的齐格勒-尼可尔斯整定方法与模糊控制相结合,利用系统偏差值和偏差的变化率作为模糊控制器的输入,经过模糊推理,得到系统的修正参数ΔKp、ΔKi、ΔKd,实时修正系统比例增益、积分增益和微分增益,使系统保持在最佳的控制状态.从常规PID仿真和模糊PID仿真效果对比可见,参数自整定模糊PID控制比常规PID控制有明显的控制优势,克服了常规PID控制的缺陷,有效地抑制了超调量.其算法的应用简便且灵活.也具有较好的鲁棒性,在实际应用中容易实现,有一定的实际意义.
| [1] |
乔铁柱, 闫来清. 模糊PID控制及在恒压供液系统的应用[J].
煤炭工程, 2011(10): 95-98.
Qiao T Z, Yan L Q. Fuzzy PID control and in constant pressure for liquid system application[J]. Coal Engineering, 2011(10): 95-98. DOI: 10.3969/j.issn.1671-0959.2011.10.036. |
| [2] |
刘静纨, 魏东, 刘熙. 变风量空调系统温度模糊PID控制[J].
土木建筑与环境工程, 2009, 31(4): 98-103.
Liu J W, Wei D, Liu X. Temperature fuzzy PID control for variable air volume system[J]. Journal of Civil, Architectural&Environmental Engineering, 2009, 31(4): 98-103. |
| [3] |
强明辉, 周学文. 模糊PID算法在泡沫玻璃窑炉温度控制中的应用[J].
工业仪表与自动化装置, 2010(5): 87-90.
Qiang M H, Zhou X W. Application of fuzzy PID algorithm in foam glass furnace temprature control[J]. Industrial Instruments and Automatic Costume, 2010(5): 87-90. |
| [4] |
邱志雄. 模糊PID控制器[J].
电气自动化, 1994(4): 37-38.
Qiu Z X. Fuzzy PID controller[J]. Electrical Automation, 1994(4): 37-38. |
| [5] |
丁坚, 王革思, 李柏松. 模糊PID控制器的性能研究[J].
高新技术, 2008(9): 5.
Ding J, Wang G S, Li B S. Fuzzy PID controller performance research[J]. Science and Technology Innovation Heraid, 2008(9): 5. |
| [6] |
陶永华, 尹怡欣, 葛芦生.
新型PID控制及其应用[M]. 北京: 机械工业出版社, 1998.
|
| [7] |
刘金琨.
先进PID控制及其MATLAB仿真[M]. 3版. 北京: 电子工业出版社, 2011.
|
| [8] |
徐晓东, 徐晓辉, 任安业. 基于参数自整定模糊PID控制的大型液压源温控系统设计[J].
上海航天, 2010(5): 60-65.
Xu X D, Xu X H, Ren A Y. Design of parameters self-tuning PID fuzzy control in temperature control system of large-scale hydraulic source[J]. Aerospace Shanghai, 2010(5): 60-65. |
| [9] |
金宏平, 冯美斌, 黄志文. 模糊PID控制器的改进[J].
汽车科技, 1999(4): 40-42, 49.
|
| [10] |
朱摩西. 模糊PID控制器[J].
工业控制计算机, 1996(3): 19-20.
Zhu M X. Fuzzy PID controller[J]. Industrial control computer, 1996(3): 19-20. |
| [11] |
万百五, 韩崇昭, 蔡远利.
控制论——概念、方法与应用[M]. 北京清华大学学研大厦A座: 清华大学出版社, 2009.
|
| [12] |
王军, 韩建兵, 付占稳. 基于模糊PID控制的过程控制实验系统的研究[J].
河北科技大学学报, 2005(2): 150-153.
Wang J, Han J B, Fu Z W. Study of process control experiment based on fuzzy PID control[J]. Journal of Hebei University of Science and Technology, 2005(2): 150-153. DOI: 10.7535/hbkd.2005yx02018. |
| [13] |
张化光.
智能控制基础理论及应用[M]. 北京: 机械工业出版社, 2005.
|
| [14] |
温良, 杨明国, 贺小峰. 基于自适应遗传算法优化的模糊PID控制在实验轧机中的应用研究[J].
机床与液压, 2011, 39(17): 26-30.
Wen L, Yang M G, He X F. Application of fuzzy PID control based on AGA in experimental rolling mill[J]. Machine Tool & Hydraulics, 2011, 39(17): 26-30. DOI: 10.3969/j.issn.1001-3881.2011.17.008. |
| [15] |
殷云华, 樊水康, 陈闵鄂. 自适应模糊PID控制器的设计和仿真[J].
火力与指挥控制, 2008, 33(7): 96-100.
Yin Y H, Fan S K, Chen M E. The design and simulation of adaptive fuzzy PID controller[J]. Fire Control and Command Control, 2008, 33(7): 96-100. |
 2014, Vol. 31
2014, Vol. 31