分类是人们认识事物的基础,人们认识事物时往往先把被认识的对象进行分类,以便寻找其中同与不同的特征, 因而分类学是人们认识世界的基础科学[1].对于分类,人们已开展了大量研究,目前主要的分类方法包括贝叶斯分类器、决策树(DT,Decision Tree)、支持向量机(SVM,Support Vector Machine)、K近邻(KNN)等.其中SVM在分类中体现了突出的优势,并取得了大量的研究成果,已经在很多领域得到广泛应用,例如在回归学习、入侵检测、文本分类等领域都已广泛的应用[2-3].
支持向量机是机器学习的一种,建立在统计学习VC维理论和结构风险最小化原理基础上,由于它能够在很大程度上克服“维数灾难”和“过学习”等缺点,特别适合用来解决小样本、非线性和高维模式识别的分类预测问题[4].标准的支持向量机学习算法可以归结为求解一个受约束的二次型规划(Quadratic Programming,QP)问题[5], 但是随着训练数据集规模增大,将出现训练速度慢、效率降低、算法复杂等问题.通常的解决方法是化繁为简,训练算法按照某种迭代策略(例如支持向量机结合决策树),将原有大规模QP问题分解成一系列小的QP问题,然后反复求解小的QP问题,由小的QP问题的解构造出原有大规模QP问题的近似解,并使该近似解逐渐收敛到最优解.当前各类训练算法所面临的主要困难是如何对大规模的QP问题进行分解,以及如何选择合适的工作集[4].
本文尝试使用支持向量机和决策树解决上述问题.通过构建一种基于支持向量机和决策树的多分类器,将一个大的多分类问题分解成多个小的二分类问题,然后利用二分类SVM一一解决,最终解决预测搜索结果相关的多分类问题.决策树的每个非叶子结点是一个二分类SVM分类器,叶子结点对应所有类别,分类路径到达叶子结点,表明本次分类结束.本文中多分类模型的决策树结构采用的是哈夫曼树,其中训练模型构造过程是自下而上,分类测试过程是自上而下,以此构造的分类模型具有减少错误积累、避免局部最优解、平衡错误和快速分类等优点.
1 支持向量机与分类 1.1 支持向量机支持向量机能处理回归(时间序列分析)和模式识别(分类问题、判别分析)等诸多问题,可以应用于预测分类等学科领域.SVM通过训练样本,寻找一个将各类分开的最优分类超平面,该超平面可以保证分类精度并使其两侧的空白区域尽可能最大,即分类间隔最大化,从而实现最优分类[4].
以两类数据分类为例,对于线性可分,给定训练样本集(xi, yi),i=1, 2, 3, …, l,x∈Rn,y∈{±1},超平面记作(w·x)+b =0,为使分类面对所有样本正确分类并且具备分类间隔,就要求它满足约束
| ${\mathit{\boldsymbol{y}}_\mathit{i}}\left[{\left( {\mathit{\boldsymbol{w}} \cdot \mathit{\boldsymbol{x}}} \right) + \mathit{\boldsymbol{b}}} \right] \ge 1, i = 1, 2, \ldots, \mathit{l, } $ | (1) |
可以计算出分类间隔为
| $\min \phi \left( \mathit{\boldsymbol{w}} \right) = \frac{1}{2}{\left\| w \right\|^2}. $ | (2) |
为了解决这个约束最优化问题,引入Lagrange函数来实现对偶变量的优化求解,最终得到最优分类超平面(w*·x)+ b*=0,其中w*是最优权值向量,b*是最优偏置,而最优分类函数为
| $\begin{array}{l} f\left( \mathit{\boldsymbol{x}} \right) = {\mathop{\rm sgn}} \left\{ {\left( {{\mathit{\boldsymbol{w}}^\mathit{x}} \cdot \mathit{\boldsymbol{x}}} \right) + {\mathit{\boldsymbol{b}}^\mathit{\boldsymbol{*}}}} \right\} = \\ {\mathop{\rm sgn}} \left[{\sum\limits_{j = 1}^l {\mathit{\boldsymbol{a}}_j^*{\mathit{\boldsymbol{y}}_\mathit{j}}\left( {{\mathit{\boldsymbol{x}}_\mathit{j}} \cdot {\mathit{\boldsymbol{x}}_\mathit{i}}} \right) + {\mathit{\boldsymbol{b}}^\mathit{\boldsymbol{*}}}} } \right], \mathit{\boldsymbol{x}} \in {\mathit{\boldsymbol{R}}^\mathit{n}}. \end{array} $ | (3) |
对于线性不可分情况,SVM的主要思想是将输入向量映射到一个高维的特征向量空间,并在该特征空间中构造最优分类面.将x从输入空间Rn到特征空间H的变换ϕ,得:x→ϕ(x)以特征向量ϕ(x)代替输入向量x,则可以得到最优分类函数为
| $f\left( \mathit{\boldsymbol{x}} \right) = {\mathop{\rm sgn}} \left( {\mathit{\boldsymbol{w}} \cdot \phi \left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{b}}} \right) = {\mathop{\rm sgn}} \left[{\sum\limits_{j = 1}^l {{\mathit{\boldsymbol{a}}_\mathit{i}}{\mathit{\boldsymbol{y}}_\mathit{i}}\phi \left( {{\mathit{\boldsymbol{x}}_\mathit{i}}} \right)} \cdot \phi \left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{b}}} \right]. $ | (4) |
为了避免直接在高维空间中进行计算,引入了核函数机制,其中K(xi, x)就是核函数,上式变换为
| $f\left( \mathit{\boldsymbol{x}} \right) = {\mathop{\rm sgn}} \left( {\mathit{\boldsymbol{w}} \cdot \phi \left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{b}}} \right) = {\mathop{\rm sgn}} \left[{\sum\limits_{j = 1}^l {{\mathit{\boldsymbol{a}}_\mathit{i}}{\mathit{\boldsymbol{y}}_\mathit{i}}\phi K\left( {{\mathit{\boldsymbol{x}}_\mathit{i}}, \mathit{\boldsymbol{x}}} \right)} + \mathit{\boldsymbol{b}}} \right]. $ | (5) |
SVM本质上是二值分类,最初是针对两类分类问题提出的,不能直接用于多分类问题,而在实际应用中,往往需要解决多类分类问题,通常采用“分治”策略,即将多分类问题分解成多个二分类问题,然后构造一系列SVM二值分类器与它们对应[6-7].目前主要有3种“分治”策略:一对多,即所有类中的一类作为正类,剩下所有类作为负类,需要N-1个分类器;一对一,即N个类一对-相互组对, 每对对应一个二分类SVM,共需要(N-1)/2个分类器;SVM决策树,即将N个类对应于一棵决策树叶子结点,而所有非叶子结点为一个SVM分类器,需要构造N-1个分类器,其分类性能优于一对多和一对一组合方法[8].决策树层次结构的设计是影响SVM决策树多类分类器性能的关键之一.
2 基于哈夫曼树和SVM的多类分类器基于SVM和决策树的多类分类问题转换为构造分类模型与应用该模型进行分类两个阶段,其中构造过程是构建SVM决策树模型,分类就是利用该模型对未知类别的样本数据进行类别判断,或对已知类别的样本数据进行预测验证[9].本文分类器应用的数据是网络用户搜索行为的原始记录,该数据是不规则的、非数值的,并且存在噪声,通过数据预处理将其转化规范的数据集,然后划分为训练集和测试集两部分,其中训练集用来构造分类模型,测试集用来实现分类应用.分类器模型如图 1所示,具体过程分述如下.
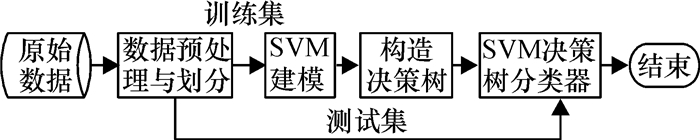
|
图 1 分类器模型 Figure 1 Classifier model |
分类模型的构造过程是自下而上的,如图 2所示,训练从决策树的叶子结点出发,依据某种决策方法来区分类间的可分性,每次都将最不好分的两类作为训练样本的正负类.训练完毕后,得到的一个二分类SVM作为决策树模型的一个非叶子结点,合并其对应的正负两类成为一个新的类簇(一个或多个类组成)[10],参与下一次训练.如此循环,直到剩下最后两个类簇(或类)作为训练的正负类,训练后得到的二分类SVM作为决策树的根结点.至此,基于SVM和决策树的多分类器训练模型构造完成.
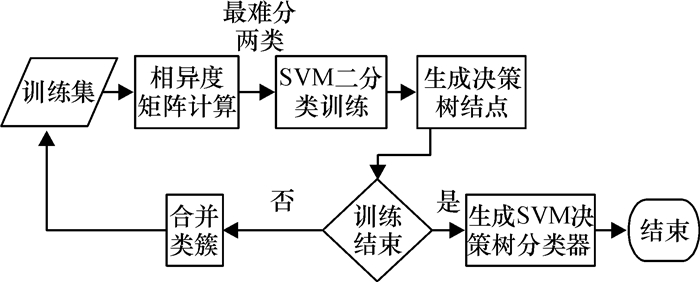
|
图 2 分类器的构造过程 Figure 2 Construction of the classifier |
测试与分类过程是训练过程的逆过程,自上而下,如图 3所示.首先,从分类模型的根结点开始,使用根结点对应的二分类SVM,对分类样本进行分类预测;根据预测的中间结果,分类到达决策树的下一层某个分支结点,然后使用该结点对应的二分类SVM对样本进行分类预测.重复此过程,分类最终到达决策树的某一个叶子结点,该叶子结点对应的类别就是本次分类的结果,本次样本分类结束.

|
图 3 多分类过程 Figure 3 Multi-class classification process |
其中测试过程是构造多分类器的一部分,其目的是验证分类器的分类准确率性能.测试过程用到的测试集样本的分类标签为已知,测试样本被分类器分类之后得到的分类标签与已知标签相同时,表示分类正确,此时正确分类样本数加一.所有样本测试结束之后,分类准确率=(正确分类样本数/测试集样本数)×100%.分类过程的样本分类标签未知,不用求解分类准确率.
2.3 相异度计算SVM分类对于训练样本在原始空间线性可分的情况,各类样本间距离反映了它们的可分性.距离越大,越容易正确分类,距离越小,分类误差越大.对于线性不可分的情况,样本间的可分性很难直接在原始空间计算样本间的距离反映出来,因此必须有一种策略可以将样本从原始空间映射到特征空间,将线性不可分转换为线性可分.支持向量机通过变换核函数将样本映射到特征空间,不能保证映射前后样本间的欧氏距离不变或成比例变化,但是样本在特征空间的距离度量可以体现样本间的可分性[11].
类间相异度是在特征空间计算的,用来度量两个类的差别程度,值越大,表示两个类差别越大越好分;值越小,表示两个类差别越小越难分.类间相异度矩阵在优先选择最不好分的两类进行训练时,起到了决策作用.
定义1 给定N类训练样本集{X1, X2, X3, …, XN},其中第i类样本为Xi={x1i, x2i, x3i, …, xnii},分别为每类的训练样本构造一超球面,得到球面集合,类间相异度矩阵D为
| $\mathit{\boldsymbol{D = }}\left| {\begin{array}{*{20}{c}} {{D_{11}}}&{{D_{12}}}& \cdots &{{D_{1N}}}\\ {{D_{21}}}&{{D_{22}}}& \cdots &{{D_{2N}}}\\ \vdots & \vdots &{}& \vdots \\ {{D_{N1}}}&{{D_{N2}}}& \cdots &{{D_{NN}}} \end{array}} \right|, $ | (6) |
| ${D_{ij}}\frac{{{N_{ij}}\left( {{d_{ij}}} \right) + {N_{ji}}\left( {{d_{ji}}} \right)}}{{{\mathit{n}_\mathit{i}} + {n_j}}} \times {d_{\left( {i, j} \right)}} \in \left[{0, 1} \right], $ | (7) |
| $d = \frac{{\sum\limits_{k = 0}^{{n_i}} {\left( {\mathit{\boldsymbol{x}}_k^i - {c_j}} \right)} }}{{{n_i}}}. $ | (8) |
式(6)中Dij表示两个类Xi和Xj之间的相异度,其中i, j=1, 2, 3, …, N.式(7)中dij表示Xi的所有样本到Xj对应超球体中心的平均欧氏距离,Nij(dij)表示Xi中的训练样本到Xj的超球体中心的欧氏距离大于dij的所有样本数量,d(i, j)为Xi和Xj的超球体中心之间的欧氏距离,ni、nj分别为Xi和Xj的样本数.
式(7)中,Dij表达式的前半部分
分析相异度公式可知,相异度矩阵是对称的,可以节省一部分计算时间.
2.4 基于正态树的SVM多分类器根据二叉树的结构,可以将决策树分为两种类型:偏态树和正态树[8],如图 4所示.
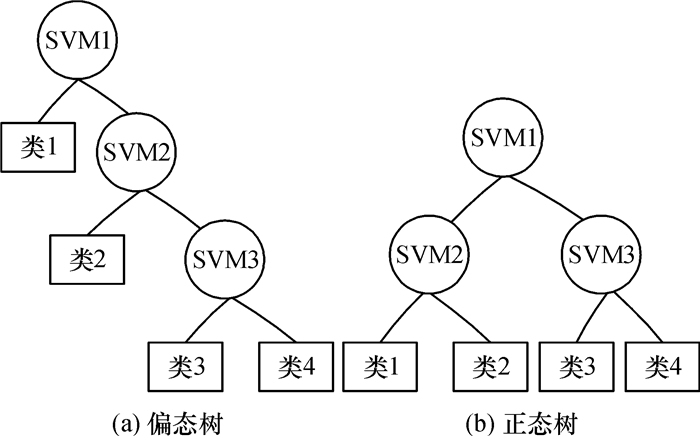
|
图 4 决策树的两种结构 Figure 4 Two kinds of structures of the decision tree |
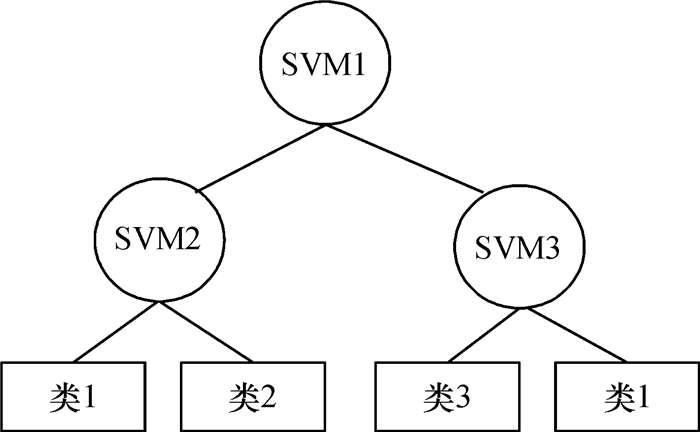
传统的基于正态树的SVM决策树多分类方法为了使决策树的层次最少,以追求最大的平衡错误效果,采用的是自上而下的训练方式,总是将当前认为最好分的两类作为优先训练的目标,这种做法会产生局部最优解,但不一定是整体最好分的目标,因此容易进入贪心算法的陷阱.另外,为了得到一个好的训练结果,首先将整个训练集划分为两部分,如图 5所示,分离面1分别将类1、类2和类1、类3划分开来,其中类1对应的样本集被划分成了两个子集,最终导致类1有两条不同的分类路径.如图 6所示,类1有SVM1→SVM2→类1和SVM1→SVM3→类1两条分类路径,相当于增加了总的分类路径,在某种程度上影响了分类速度.
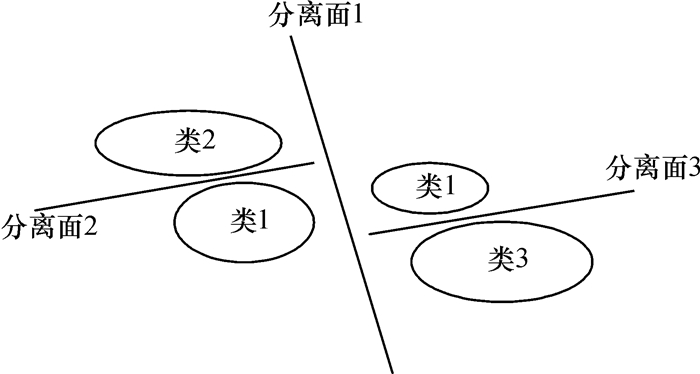
|
图 5 传统决策树分类 Figure 5 Classification of the traditional decision tree |
|
图 6 包含重复路径的正态树 Figure 6 Normal tree containing repeated paths |
为了克服贪心算法的缺点,在此基础上本文构造了以偏态树结构为基础的SVM决策树多分类器.其思路是,首先计算N个类之间的相异度,从决策树最底层的叶子结点开始,根据相异度矩阵,将训练集中相异度最小的两类划分为正负类,并且作为决策树的两个叶子结点,进行SVM二值分类,对应的SVM为决策树的一个非叶子结点,将它们合并为一个新的类簇,作为下一次SVM训练的负类.然后,重新计算剩下N-2个类与该负类的相异度,选择与之相异度最小那个类作为正类,再次进行SVM二值分类.重复以上过程,直到将原训练集中的所有类别训练结束,最后一次训练的SVM作为决策树的根结点.
以偏态树结构为基础的SVM决策树多分类和传统的以正态树结构为基础的SVM决策树多分类在训练过程的区别是,前者得到的当前最不好分的两类是局部最优解;后者得到的当前最不好分的两类是全局最优解.它们都要构造N-1个SVM二值分类器,其分类都是从根结点开始,结束于叶子结点.
对比图 4、图 5发现,对于4类分类问题,基于偏态树的多分类模型和基于正态树的多分类模型都构造了3个SVM二值分类器,前者为4层树,后者为3层树.在决策树每层的分类中,若在上层的某个结点发生了分类错误,则会把错误延续到该结点后续的下一层结点上.尤其离根结点越近的地方发生错误,最终的分类误差累积越大,若类别N较大时,这种错误累积是致命的.为了获得好的泛化性能,应由可分性强的类作为决策树的上层结点定义分类子任务.正态树能有效地减少决策树的层数,因此在构建决策树模型时,正态树结构是优先考虑的方法.
2.6 基于哈夫曼树的SVM构建为此,本文进一步改进,提出了基于哈夫曼树的决策树分类器.
哈夫曼树定义:给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小或最大,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman tree).
哈夫曼树是由n个带权叶子结点构成的所有二叉树中带权路径长度最短的二叉树.哈夫曼算法是一种非贪心算法,实验证明哈夫曼树比偏态及正态树分类更优越,是相对更理想的选择.另外哈夫曼树采用自下而上的顺序构造,避免产生一个类对应多条分类路径的情况.
以哈夫曼树结构为基础的SVM决策树多分类的训练思路是,首先计算N个类之间的相异度矩阵,从决策树的叶子结点开始,选择训练集中相异度最小的两类,进行SVM二值分类训练,对应的SVM为决策树的一个非叶子结点.然后,将这两类合并为一个新的类簇,与剩下的N-2个类组成包含N-1个类(或类簇)的训练集.重新计算这N-1个类(或类簇)之间的相异度矩阵,再次选择相异度最小的两类进行SVM二值分类训练.重复该过程,直到将原训练集中的所有类别训练结束,最后一次训练的SVM二值分类器为决策树分类模型的根结点.
本文中哈夫曼树结构的带权路径是用类间相异度来度量的.两个类间相异度越小,说明两个类的特征越相近,表示这两类越不容易分类,因此优先将相异度最小的两个类合并为一个类簇,作为决策树当前SVM结点的训练集.这样一来,该次训练离决策树根结点相对最远,其对应的分类过程产生的误差积累对最终分类结果的影响将减少到最小.具体过程如下:
Step1:计算出训练集中N个类的类间相异度矩阵.
Step2:根据类间相异度矩阵,在所有N个类中选择Dij最小的两类Xi和Xj.并对Xi和Xj进行两类支持向量机训炼,构建关于Xi和Xj的两类SVM分类器,作为决策树的一个结点.
Step3:将Xi和Xj对应的集合合并作为一个新的类簇,与剩下的N-2个类组成包含N-1个类簇的训练集,计算出这N-1个类的相异度矩阵.
Step4:依照上述方法,在刚才得到的N-1个类簇中选择类间相异度最小的两个类进行SVM二分类训练.
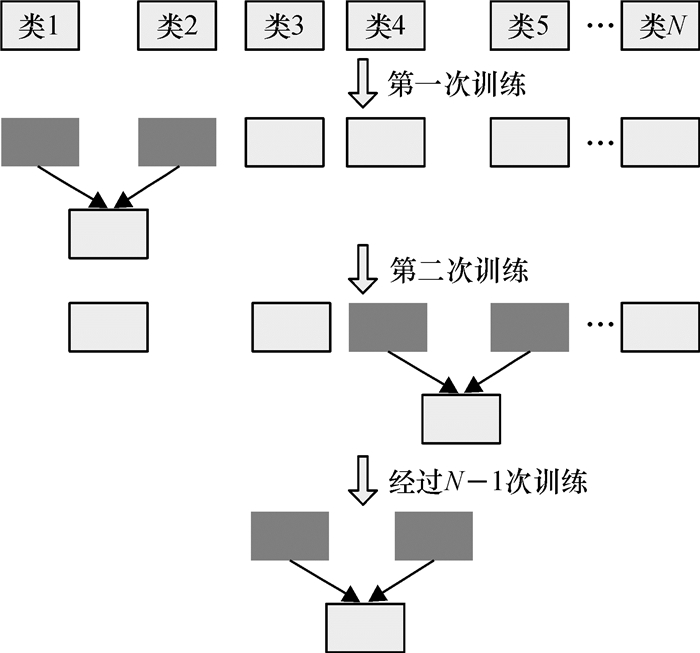
Step5:重复以上过程,直到剩下最后2个类簇,构建关于它们的SVM二分类器,并将该分类器作为最终决策树的根结点,训练结束后合并两类得到一个包含所有类的类簇,基于SVM和决策树的多分类的训练模型构建完毕.图 7是构建模型过程中训练集的合并过程,每合并一次就有一个二分类SVM与其对应.
|
图 7 样本集的合并过程 Figure 7 The merging process of sample sets |
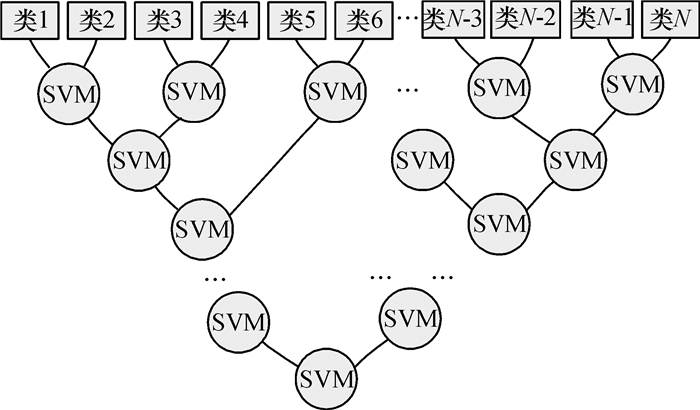
对于N类训练集,每一次训练过程将具有类间最小相异度的两个类簇进行二分类SVM训练,训练得到的SVM作为决策树的一个非叶子结点,参与训练的两个类簇合并成一个新类簇.经过N-1次训练后,将得到一个倒置的最优二叉树,树中叶子结点对应的是每个类,非叶子结点是二分类SVM,如图 8所示.
|
图 8 SVM决策树多分类器 Figure 8 Multi-class classification based on SVM and decision tree |
哈夫曼树是最优二叉树,其结构特征处于偏态树和正态树,在此基础上构造一种自下而上的基于SVM的多分类决策树模型,不但可以避免陷入产生局部最优解的贪心算法中,也能够平衡分类错误并减少错误累积,提升总体分类精度和速度.
2.7 基于哈夫曼树的SVM分类上一节构建的基于哈夫曼树的SVM决策树多分类器中,每一个非叶子结点对应一个SVM二值分类器,每个叶子结点对应一个类别.分类从决策树的根结点开始,利用每一个非叶子结点对应的SVM二值分类器对经过该结点的样本进行分类.根据分类的结果确定样本是属于左子树还是右子树.若所属的子树刚好为一个叶子结点,则本次分类结束,该叶子结点对应的类别便是该样本的最终分类结果.
3 实验及结果分析实验数据:选自第一届勒卡斯数据挖掘竞赛提供的第二题数据集[12],该数据集是基于搜索关键字的原始数据,其中存在一定数量的噪声数据,经过数据预处理之后,本文从中选取了8 294条数据作为样本数据集,该样本数据集拥有10个类别,每类包含的样本数在500条至1 100条之间.将每类样本数据按照3: 1的比例划分为训练集和测试集.
本文采用了3种方法进行实验,这3种方法分别为:传统的SVM多分类方法(方法1)[13]、基于偏态树的SVM决策树多分类方法(方法2)和基于哈夫曼树的SVM决策树多分类方法(方法3).其中方法1是在Matlab环境下使用Iibsvm工具包进行的,其他方法2、方法3是在VC+ +6.0中使用libsvm工具包完成的.支持向量机使用的是RBF核,并且使用了libsvm提供的grid.py和easy.py做了关于(C,gamma)的交叉验证参数选择.表 1列出了所有类样本数量及3种方法对应各类的实验结果.
| 表 1 样本数量及测试结果 Table 1 Number of samples and test results |
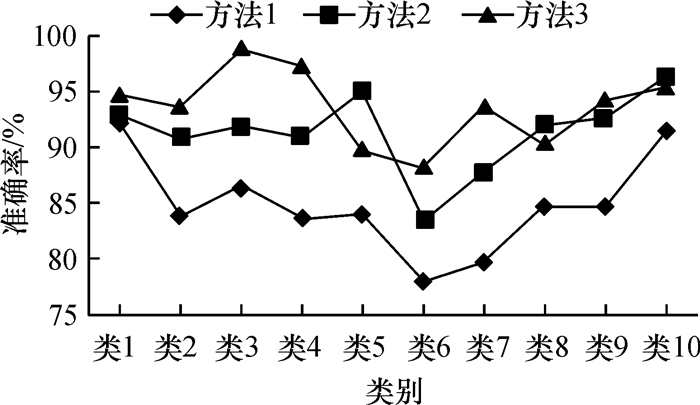
从表 1看出,基于SVM和决策树的多分类方法较普通的SVM多分类方法,分类精度有很大程度的提高;基于哈夫曼树的SVM决策树多分类方法较普通的SVM多分类方法和基于偏态树的SVM决策树多分类方法,能得到更高的分类精度.每类对应的分类准确率如图 9所示,更加形象地验证了这一点.
|
图 9 3种多分类方法分类准确率 Figure 9 Accuracy of three multi-class classification methods |
表 2列出了3种多分类方法的实验结果对比,包括总的分类精度、训练时间及测试时间.从表 2中可以看出,普通的SVM多分类方法的训练时间、分类测试时间远多于基于支持向量机和决策树多分类方法,而且在分类精度上也逊色很多.另外,基于SVM及正态决策树(本文用到的是哈夫曼树)多分类方法和基于SVM及偏态决策树多分类方法相比,在分类精度上,前者较后者提升了将近3.5%,这说明基于正态树结构的分类模型能有效减少分类过程中的误差积累;在训练速度上,前者比后者慢了8 s左右,这是因为基于正态树的SVM多分类方法中,每次计算相异度矩阵是多对多的,消耗了更多的时间.
| 表 2 3种多分类方法的结果 Table 2 Results of three multi-class classification methods |
本文利用类间相异度为决策依据,构建了以哈夫曼树结构为基础的SVM决策树的多分类方法,克服了产生局部最优解的缺点并削弱了错误累积的影响,较普通的SVM多分类方法,在分类精度和分类速度上都有很大程度上的提高.另外,基于偏态树结构的SVM多分类方法拥有更快的训练速度,基于哈夫曼树的SVM多分类方法拥有更高的分类精度.最后将本文的方法应用于网络搜索数据上,证明了该结论.针对不同的应用,如何选择不同的决策树型结构构造多分类模型来平衡训练时间和分类精度之间的关系,从而最大程度地发挥不同决策树型结构的优点,这需要在后续的研究工作中继续探讨.
| [1] |
王燕爽. 分类能力与学习成绩[D]. 吉林: 东北师范大学外国语学院, 2006.
|
| [2] |
Teng S H, Du H L, Wu N Q. A cooperati-ve network intrusion detection based on fuzzy SVMs[J].
Journal of Networks, 2012, 5(4): 475-483.
|
| [3] |
Zhang W, Teng S H, Zhu H B. Fuzzy multi-class support vector machines for cooperative network intrusion detection[C]. Proceedings of the 9th IEEE International Conference on Cognitive Informatics(ICCI), Beijing, 2010: 811-818.
|
| [4] |
丁世飞, 齐丙娟, 谭红艳. 支持向量机理论与算法研究综述[J].
电子科技大学学报, 2011, 40(1): 2-10.
Ding S F, Qi B J, Tan H Y. An over-view on theory and algorithm of support vector machines[J]. Journal of University of Electr-onic Science and Technology of China, 2011, 40(1): 2-10. |
| [5] |
刁智华, 赵春江, 郭新宇. 一种新的基于平衡决策树的SVM多类分类算法[J].
控制与决策, 2011, 26(1): 149-152.
Diao Z H, Zhao C J, Guo X Y. A new SVM multi-class classification algorithm based on balance decision tree[J]. Control and Decision, 2011, 26(1): 149-152. |
| [6] |
杜红乐. 基于支持向量机的协同入侵检测[D]. 广州: 广东工业大学计算机学院, 2009.
|
| [7] |
崔建, 李强, 刘勇. 基于决策树的快速SVM分类方法[J].
系统工程与电子技术, 2011, 33(1 1): 2558-2563.
Cui J, Li Q, Liu Y. Fast SVM classifi- cation method based on the decision tree[J]. System Engineering and Electronics, 2011, 33(1 1): 2558-2563. |
| [8] |
赵天昀. 一种改进的SVM决策树文本分类算法[J].
情报杂志, 2010, 29(8): 141-143.
Zhao T J. Text classifier based on an improved SVM decision tree[J]. Journal of Intelligence, 2010, 29(8): 141-143. |
| [9] |
厉小润, 赵光宙, 赵辽英. 决策树支持向量机多分类器设计的向量投影法[J].
控制与决策, 2008, 23(7): 745-750.
Li X R, Zhao G Z, Zhao L Y. Design of decision-tree-based support vector machines multi-class classifier based on vector projection[J]. Control and Decision, 2008, 23(7): 745-750. |
| [10] |
张先武, 郭雷. 一种新的支持向量机决策树设计算法[J].
火力与指挥控制, 2010, 35(10): 31-35.
Zhang X W, Guo L. A new algorithm for designing SVM with decision tree architecture[J]. Fire Control & Command Control, 2010, 35(10): 31-35. DOI: 10.3969/j.issn.1002-0640.2010.10.009. |
| [11] |
乔增伟, 孙卫祥. 一种基于支持向量机决策树多类分类器[J].
计算机应用与软件, 2009, 26(11): 227-230.
Qiao Z W, Sun W X. A Multi-class classifier based on SVM decision tree[J]. Computer Applications and Software, 2009, 26(11): 227-230. DOI: 10.3969/j.issn.1000-386X.2009.11.075. |
| [12] |
勒卡斯集团. 第一届勒卡斯杯数据挖掘竞赛(上海站)[DB/OL].
[2014-03-20]. http://ledmclub.engagecloud.net/. |
| [13] |
裘国永, 张娇. 基于二分K-均值的SVM决策树自适应分类方法[J].
计算机应用研究, 2012, 29(10): 3685-3687.
Qiu G Y, Zhang J. Adaptive SVM decisi-on tree classification algorithm based on bisecting K-means[J]. Application Research of Computers, 2012, 29(10): 3685-3687. DOI: 10.3969/j.issn.1001-3695.2012.10.021. |
 2014, Vol. 31
2014, Vol. 31