微腔在量子光学和量子信息及量子计算中有许多应用, 被广泛用于将原子与光子纠缠、产生原子量子比特、研究退相干等现象[1-3].近年来, 耦合腔在量子信息处理中的作用引起了人们的兴趣[4-10], 利用耦合腔可以实现量子态传递、量子相位门等.耦合腔与原子相互作用系统和单腔-原子相互作用系统相比, 一个优势是通过调节腔之间耦合强度就可以控制原子之间相互作用而不必操作原子自身.事实上, 内含量子点的耦合腔早就在实验中实现[11].笔者曾研究过隧穿耦合量子点分子与单模场相互作用系统的几何相位[12]及腔场的相位[13]问题, 由于该量子点分子模型控制方面的灵活性而引起一些研究人员的关注[14-16].鉴于量子点在固体量子信息处理器件方面的应用前景, 本文考虑两个耦合腔分别放入一个量子点和一个上述隧穿耦合量子点分子系统中的量子纠缠性质.
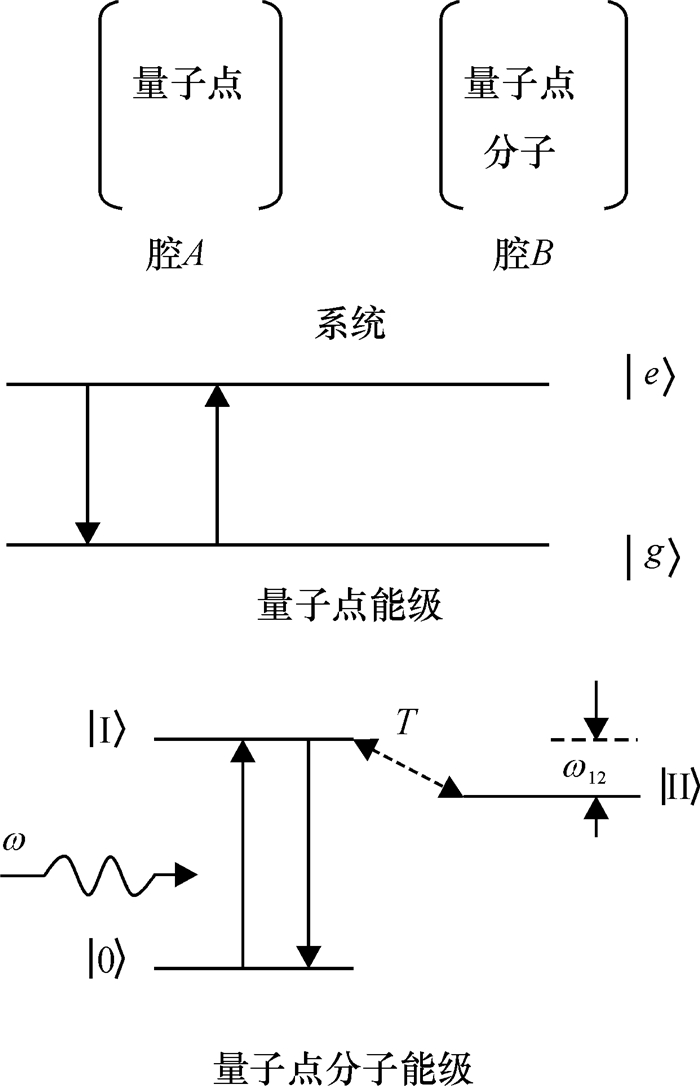
1 理论模型及系统态矢量本文研究的系统如图 1所示, 由两个分别放入一个二能级的量子点微腔A和放入一个隧穿耦合的量子点分子的微腔B构成, 其中两微腔之间通过渐逝场相互耦合, 微腔A中量子点及微腔B中量子点分子的能级结构也示于图 1中, ω为腔场频率.笔者曾研究过这里的量子点分子与腔场复合系统的量子相位问题, 量子点分子简化为三能级系统的具体原因见文献[17].
|
图 1 系统与量子点、量子点分子能级示意图 Figure 1 Diagrams of the system, energy levels of the quantum dot and the quantum dot molecule |
为简单起见, 假定量子点与腔场A及量子点分子与腔场B分别发生共振相互作用, |Ⅰ〉, |Ⅱ〉能级也共振(ω12=0), 则在旋波近似下和相互作用表象中, 系统的哈密顿量可以表示为(ℏ=1)[8, 12]
| $ \begin{array}{l} \hat H = f({a_A}{s_1}^† + {a_A}^† {s_1}^ - ) + g({a_B}{\rm{|Ⅰ}}\rangle \langle 0| + {a_B}^† 0\rangle \langle {Ⅰ}) + \\ T\left( {|{Ⅱ}\rangle \langle {\rm{Ⅰ|}} + |{Ⅰ}\rangle \langle {Ⅱ}|} \right) + J({a_A}{a_B}^† + {a_A}^† {a_B}), \end{array} $ | (1) |
其中, aA, aA† (aB, aB†)分别为两腔场模的湮没和产生算符, s1†和s1-是量子点的赝自旋算符, |i〉〈j|(i, j=0, Ⅰ, Ⅱ)对应于量子点分子的跃迁算符, f和g分别为腔中的量子点与其所在腔的腔场之间的耦合系数, T是电子隧穿矩阵元, J是两个腔之间的耦合系数.
设初始时刻, 量子点处于激发态, 量子点分子处于基态, 腔场A和B均处于真空态, 则系统的初态为
| $ |\psi \left( 0 \right)\rangle = |{e_1}\rangle |{0_2}\rangle |{0_A}\rangle |{0_B}\rangle , $ | (2) |
式(2)中下标1, 2分别对应量子点和量子点分子.在演化过程中, 系统将保留在基矢
| $ \begin{array}{l} \{ |{\varphi _1}\rangle = |{e_1}\rangle |{0_2}\rangle |{0_A}\rangle |{0_B}\rangle , \\ |{\varphi _2}\rangle = |{g_1}\rangle |{{Ⅰ}_2}\rangle |{0_A}\rangle |{0_B}\rangle , \\ |{\varphi _3}\rangle = |{g_1}\rangle |{Ⅰ}{{Ⅰ}_2}\rangle |{0_A}\rangle 0{|_B}\rangle , \\ |{\varphi _4}\rangle = |{g_1}\rangle |{0_2}\rangle |{1_A}\rangle |{0_B}\rangle , \\ |{\varphi _5}\rangle = |{g_1}\rangle |{0_2}\rangle |{0_A}\rangle |{1_B}\rangle \} \end{array} $ |
张成的子空间中.在该子空间中, 系统的哈密顿算符的矩阵表示为
| $ \mathit{\boldsymbol{H}} = \left( {\begin{array}{*{20}{c}} 0&0&0&f&0\\ 0&0&T&0&g\\ 0&T&0&0&0\\ f&0&0&0&J\\ 0&g&0&J&0 \end{array}} \right), $ | (3) |
其本征值为
| $ \begin{array}{l} {E_1} = 0, \\ {E_{2, 3}} = \pm \alpha , \\ {E_{4, 5}} = \pm \beta , \end{array} $ | (4) |
其中,
| $ \begin{array}{l} \alpha = {\left( {\frac{{{f^2} + {g^2} + {T^2} + {J^2} + \sqrt {{{({f^2} + {g^2} + {T^2} + {J^2})}^2} - 4({f^2}{g^2} + {f^2}{T^2} + {T^2}{J^2})} }}{2}} \right)^{\frac{1}{2}}}, \\ \beta = {\left( {\frac{{{f^2} + {g^2} + {T^2} + {J^2} - \sqrt {{{({f^2} + {g^2} + {T^2} + {J^2})}^2} - 4({f^2}{g^2} + {f^2}{T^2} + {T^2}{J^2})} }}{2}} \right)^{\frac{1}{2}}}. \end{array} $ | (5) |
相应的本征态为
| $ \begin{array}{l} \;\;\;{\phi _1} = {P_1}\left( { - \frac{J}{f}|{\varphi _1}\rangle - \frac{g}{T}|{\varphi _3}\rangle + |{\varphi _5}\rangle } \right), \\ \;\;\;{\phi _2} = {P_2}\left( {\frac{f}{\alpha }|{\varphi _1}\rangle + \frac{{{\alpha ^2} - {f^2} - {J^2}}}{{Jg}}|{\varphi _2}\rangle + } \right.\\ \left. {\frac{{{\alpha ^2} - {f^2} - {J^2}}}{{Jg\alpha }}T|{\varphi _3}\rangle + |{\varphi _4}\rangle + \frac{{{\alpha ^2} - {f^2}}}{{J\alpha }}|{\varphi _5}\rangle } \right), \\ \;\;\;{\phi _3} = {P_3}\left( { - \frac{f}{\alpha }|{\varphi _1}\rangle + \frac{{{\alpha ^2} - {f^2} - {J^2}}}{{Jg}}|{\varphi _2}\rangle - } \right.\\ \left. {\frac{{{\alpha ^2} - {f^2} - {J^2}}}{{Jg\alpha }}T|{\varphi _3}\rangle + |{\varphi _4}\rangle - \frac{{{\alpha ^2} - {f^2}}}{{J\alpha }}|{\varphi _5}\rangle } \right), \\ \;\;\;{\phi _4} = {P_4}\left( {\frac{f}{\beta }|{\varphi _1}\rangle + \frac{{{\beta ^2} - {f^2} - {J^2}}}{{Jg}}|{\varphi _2}\rangle + } \right.\\ \left. {\frac{{{\beta ^2} - {f^2} - {J^2}}}{{Jg\beta }}T|{\varphi _3}\rangle + |{\varphi _4}\rangle + \frac{{{\beta ^2} - {f^2}}}{{J\beta }}|{\varphi _5}\rangle } \right), \\ \;\;\;{\phi _5} = {P_5}\left( { - \frac{f}{\beta }|{\varphi _1}\rangle + \frac{{{\beta ^2} - {f^2} - {J^2}}}{{Jg}}|{\varphi _2}\rangle - } \right.\\ \left. {\frac{{{\beta ^2} - {f^2} - {J^2}}}{{Jg\beta }}T|{\varphi _3}\rangle + |{\varphi _4}\rangle - \frac{{{\beta ^2} - {f^2}}}{{J\beta }}|{\varphi _5}\rangle } \right). \end{array} $ | (6) |
其中,
| $ \begin{array}{l} \;\;\;\;\;\;{P_1} = 1/\sqrt {\frac{{{g^2}}}{{{T^2}}} + \frac{{{T^2}}}{{{f^2}}} + 1} , \\ {P_2} = 1/\sqrt {\frac{{{f^2}}}{{{\alpha ^2}}} + {{\left( {\frac{{{\alpha ^2} - {f^2} - {J^2}}}{{Jg}}} \right)}^2} + {T^2}{{\left( {\frac{{{\alpha ^2} - {f^2} - {J^2}}}{{Jg\alpha }}} \right)}^2} + {{\left( {\frac{{{\alpha ^2} - {f^2}}}{{J\alpha }}} \right)}^2} + 1} , \\ {P_4} = 1/\frac{{{f^2}}}{{{\beta ^2}}} + {\left( {\frac{{{\beta ^2} - {f^2} - {J^2}}}{{Jg}}} \right)^2} + {T^2}{\left( {\frac{{{\beta ^2} - {f^2} - {J^2}}}{{Jg\beta }}} \right)^2} + {\left( {\frac{{{\beta ^2} - {f^2}}}{{J\beta }}} \right)^2} + 1, \\ \;\;\;\;{P_3} = {P_2}, {P_5} = {P_4}. \end{array} $ | (7) |
则初态可表示为
| $ \begin{array}{l} \mathit{|\Psi }\left( 0 \right)\rangle = A|{\phi _1}\rangle + B|{\phi _2}\rangle + C|{\phi _3}\rangle + D|{\phi _4}\rangle + \\ E|{\phi _5}\rangle . \end{array} $ | (8) |
其中,
| $ \begin{array}{l} B = \frac{{\alpha f[{g^2}({\beta ^2} - {f^2}) + {T^2}({\beta ^2} - {f^2} - {J^2})]}}{{2{P_2}({\beta ^2} - {\alpha ^2})({f^2}{g^2} + {f^2}{T^2} + {T^2}{J^2})}}, \\ D = \frac{{\beta f[{g^2}({\alpha ^2} - {f^2}) + {T^2}({\alpha ^2} - {f^2} - {J^2})]}}{{2{P_4}({\alpha ^2} - {\beta ^2})({f^2}{g^2} + {f^2}{T^2} + {T^2}{J^2})}}, \\ A = \frac{1}{{{P_1}}}(2B{P_2}\frac{{{f^2} - {\alpha ^2}}}{{J\alpha }} + 2D{P_4}\frac{{{f^2} - {\beta ^2}}}{{J\beta }}), \\ C = - B, E = - D. \end{array} $ | (9) |
由此可得, 任意时刻系统的态矢量是
| $ \begin{array}{l} \mathit{|\Psi }\left( t \right)\rangle = F|{\varphi _1}\rangle + G|{\varphi _2}\rangle + H|{\varphi _3}\rangle + I|{\varphi _4}\rangle + \\ K|{\varphi _5}\rangle . \end{array} $ | (10) |
其中,
| $ \begin{array}{l} \;\;\;F = - {P_1}A\frac{J}{f} + 2{P_2}B\frac{f}{\alpha }\cos \alpha t + 2{P_4}D\frac{f}{\beta }\cos \beta t, \\ \;\;\;G = - 2{\rm{i}}{P_2}B\frac{{{\alpha ^2} - {f^2} - {J^2}}}{{Jg}}\sin \alpha t - 2{\rm{i}}{P_4}D\frac{{{\beta ^2} - {f^2} - {J^2}}}{{Jg}}\\ \sin \beta t, \\ \;\;\;H = \left( { - {P_1}A\frac{g}{T} + 2{P_2}BT\frac{{{\alpha ^2} - {f^2} - {J^2}}}{{Jg\alpha }}\cos \alpha t + } \right.\\ \left. {2{P_4}DT\frac{{{\beta ^2} - {f^2} - {J^2}}}{{Jg\beta }}\cos \beta t} \right), \\ \;\;\;I = - 2{\rm{i}}{P_2}B\sin \alpha t - 2{\rm{i}}{P_4}D\sin \beta t, \\ \;\;\;K = {P_1}A + 2{P_2}B\frac{{{\alpha ^2} - {f^2}}}{{J\alpha }}\cos \alpha t + 2{P_4}D\frac{{{\beta ^2} - {f^2}}}{{J\beta }}\cos \beta t. \end{array} $ | (11) |
本文采用Negativity量度两子系统间的纠缠[18], 即对于用密度矩阵ρ表示的两个子系统, 其纠缠可用部分转置矩阵ρPT的负本征值来定义
| $ N = - 2\sum\limits_i {{\lambda _i}} , $ | (12) |
其中λi是部分转置矩阵ρPT的负本征值.N=0表示两个子系统是分离的;0 < N≤1表示两个子系统是纠缠的;N=1表示两个子系统处于最大纠缠态.利用(10)式, 对腔场A和B求迹, 以|e1〉|01〉, |e1〉|Ⅰ2〉, |e1〉|Ⅱ2〉, |g1〉|02〉, |g1〉|Ⅰ1〉, |g1〉|Ⅱ2〉为基矢, 可得到由量子点与量子点分子所构成的系统的密度矩阵为
| $ \begin{array}{l} {\mathit{\boldsymbol{\rho }}_1} = \\ \left( {\begin{array}{*{20}{c}} {|{F^2}|}&0&0&0&{F{G^*}}&{F{H^*}}\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&{|I{|^2} + |K{|^2}}&0&0\\ {G{F^*}}&0&0&0&{|G{|^2}}&{G{H^*}}\\ {H{F^*}}&0&0&0&{H{G^*}}&{|H{|^2}} \end{array}} \right). \end{array} $ | (13) |
利用式(12)易得量子点与量子点分子间的纠缠度
| $ \begin{array}{l} {N_1} = \sqrt {{{(|I{|^2} + |K{|^2})}^2} + 4(|HF{|^2} + |FG{|^2})} - \\ (|I{|^2} + |K{|^2}). \end{array} $ | (14) |
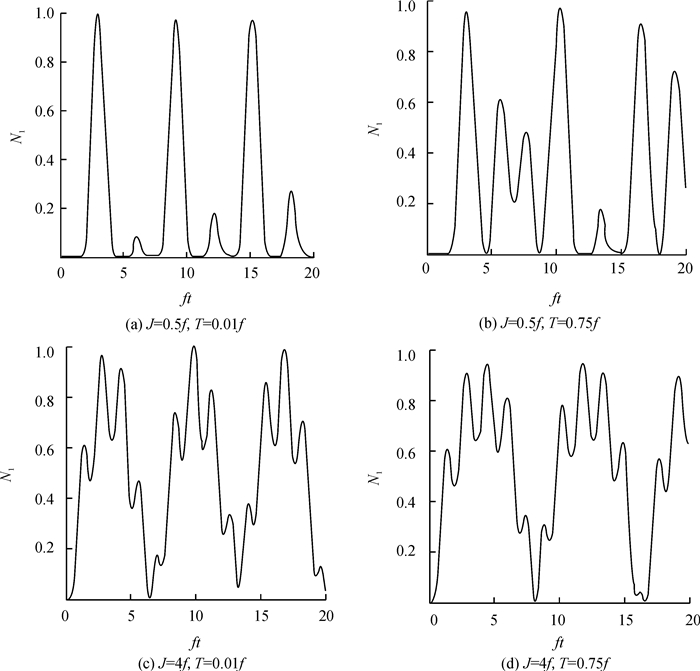
不妨取g=f, 对腔场弱耦合(J=0.5f)和强耦合(J=4f)情况, 量子点分子的隧穿强度T分别取0.01f和0.75f, 利用式(14)对N1进行数值计算, 绘制了量子点与量子点分子间的纠缠度随标度时间ft的演化规律, 如图 2所示.
|
图 2 量子点与量子点分子间纠缠度N1随时间的演化 Figure 2 Time evolution of negativity N1 of the quantum dot and the quantum dot molecule |
从图 2可以看出, 量子点与隧穿量子点分子间的纠缠度随时间作不规则振荡.比较(a)与(c)、(b)与(d)可见, 在两腔弱耦合下出现间隙消纠缠现象, 随着腔场间耦合系数的增大, N1振荡频率提高, 出现消纠缠的时间缩短而纠缠时间延长现象, 纠缠度时间平均值明显增大.通过调节在量子点分子上的外加偏压可以改变量子点分子的隧穿强度T.保持两腔耦合强度不变情况下, 在腔场弱耦合条件下增大T使得纠缠度平均值略有上升, 但纠缠度最大值却略微降低.量子点分子的隧穿强度对纠缠度影响不如两腔耦合系数大.
3 腔场A与腔场B间的纠缠特性运用式(10), 对量子点及量子点分子变量求迹, 以|0A〉|0B〉, |0A〉|ⅠB〉, |ⅠA〉|0B〉, |ⅠA〉|ⅠB〉为基矢, 可得腔场A与B所构成的系统的密度矩阵为
| $ {\mathit{\boldsymbol{\rho }}_2} = \left( {\begin{array}{*{20}{c}} {|F{|^2} + |G{|^2} + |H{|^2}}&0&0&0\\ 0&{|K{|^2}}&{K{I^*}}&0\\ 0&{I{K^*}}&{|I{|^2}}&0\\ 0&0&0&0 \end{array}} \right). $ | (15) |
利用式(12)求得腔场A与腔场B间的纠缠度
| $ \begin{array}{l} {N_2} = \sqrt {{{(|F{|^2} + |G{|^2} + |H{|^2})}^2} + 4(|IK{|^2})} - \\ (|F{|^2} + |G{|^2} + |H{|^2}). \end{array} $ | (16) |
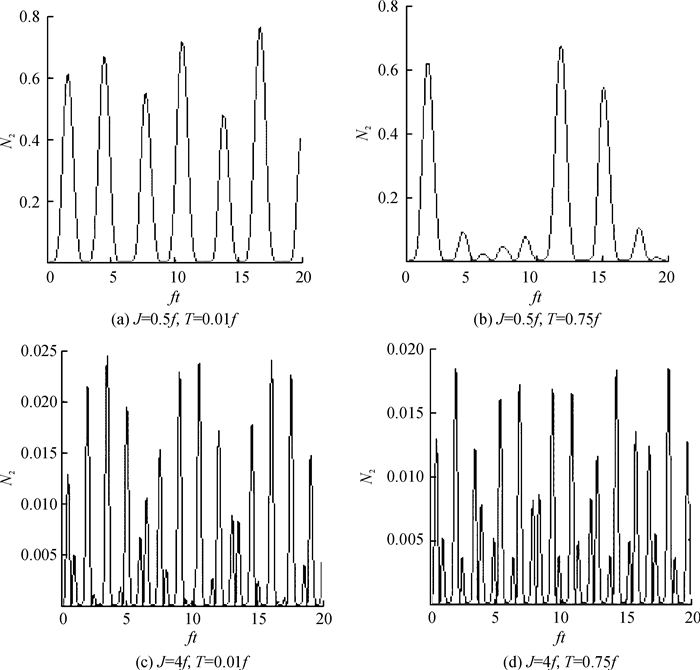
取与图 2相同参数, 根据式(16), 运用Matlab计算了腔场A与腔场B间的纠缠度, 示于图 3中.
|
图 3 腔场A与B间纠缠度N2随时间的演化 Figure 3 Time evolution of negativity N2 of fields A and B |
由图可见, 不论是在腔场弱耦合还是强耦合情况下, 腔场A与B间纠缠度都随着量子点分子隧穿程度的增加而减小;增强腔之间的耦合系数, 腔场之间的纠缠明显减小, 这里的纠缠度N2随时间振荡的频率与N1一样是提高的.任意两子系统之间纠缠度振荡频率都会随两腔耦合增大而提高这是一般性结论, 它源于式(5):当J>T时, α是J的增函数.
4 量子点与腔场A间的纠缠特性利用式(10), 对量子点分子与腔场B的变量进行求迹, 以|e1〉|0A〉, |e1〉|ⅠA〉, |g1〉|0A〉, |g1〉|ⅠA〉为基矢, 求得量子点与腔场A所构成的系统的密度矩阵为
| $ {\mathit{\boldsymbol{\rho }}_3} = \left( {\begin{array}{*{20}{c}} {|F{|^2}}&0&0&{F{I^*}}\\ 0&0&0&0\\ 0&0&{|G{|^2} + |H{|^2} + |K{|^2}}&0\\ {I{F^*}}&0&0&{|I{|^2}} \end{array}} \right). $ | (17) |
再根据式(12)计算量子点与腔场A间的纠缠度N3
| $ \begin{array}{l} {N_3} = \sqrt {{{(|G{|^2} + |H{|^2} + |K{|^2})}^2} + 4(|IF{|^2})} - \\ (|G{|^2} + |H{|^2} + |K{|^2}). \end{array} $ | (18) |
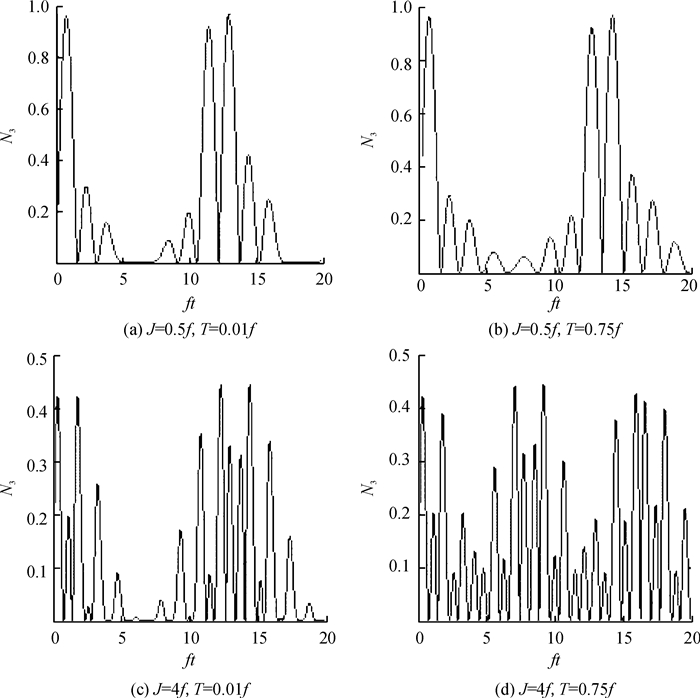
用图 2中参量对量子点与腔场A间的纠缠度进行数值计算, 在图 4中绘制了N3随时间的演化曲线.
|
图 4 量子点与腔场A间纠缠度N3随时间的演化 Figure 4 Time evolution of negativity N3 of the quantum dot and field A |
易见增大T仅使纠缠度N3稍微有所提升, 变化很小;腔场间强耦合压制了量子点与腔场A间纠缠.
5 量子点分子与腔场B间的纠缠特性量子点分子与腔场B所构成的系统的密度矩阵为
| $ {\mathit{\boldsymbol{\rho }}_4} = \left( {\begin{array}{*{20}{c}} {|F{|^2} + |I{|^2}}&0&0&0&0&0\\ 0&{|K{|^2}}&{K{G^*}}&0&{K{H^*}}&0\\ 0&{G{K^*}}&{|G{|^2}}&0&{G{H^*}}&0\\ 0&0&0&0&0&0\\ 0&{H{K^*}}&{H{G^*}}&0&{|H{|^2}}&0\\ 0&0&{00}&0&0&0 \end{array}} \right). $ | (19) |
式(12)给出量子点分子与腔场B间的纠缠度为
| $ \begin{array}{l} {N_4} = \sqrt {{{(|F{|^2} + |I{|^2})}^2} + 4(|GK{|^2} + |HK{|^2})} - \\ (|F{|^2} + |I{|^2}). \end{array} $ | (20) |
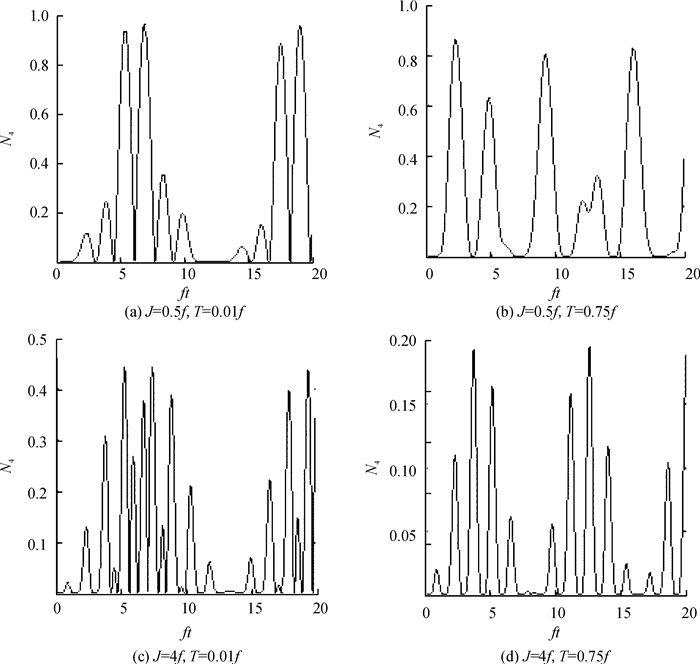
其数值计算结果如图 5所示.
|
图 5 隧穿量子点分子与腔场B间纠缠度N4随时间的演化 Figure 5 Time evolution of negativity N4 of the qumtum dot molecule and field B |
从图 5中可以看出, 量子点分子与腔场B间纠缠度N4的振荡频率随着量子点分子隧穿强度的增加而减小, N4的均值和最大值也都减小, 即随着量子点分子隧穿程度的增加, 量子点分子与腔场B间纠缠减弱.从物理角度看, 隧穿系数T增大意味着量子点分子中电子易于跃迁到能态|Ⅱ〉, 该能态中量子点分子与腔场不产生直接相互作用, 也就是说增大T相当于减弱了量子点分子与腔场B之间的能量交换, 因此降低了两者之间纠缠.至于量子点或量子点分子与腔场之间的纠缠度因两腔耦合强度增加而减小现象可通过引入退局域场模加以解释[10].本文讨论的情况等价于量子点及量子点分子与两个退局域场模之间存在失谐量为±J的非共振相互作用, 所以两腔强耦合有抑制场与量子点及量子点分子之间的能量传递的效果.由于大失谐条件难以激发场模, 因此图 3中强耦合对应两腔场模纠缠显著下降.
6 结论本文取在耦合腔A和B中分别放入一个二能级的量子点和一个三能级的隧穿量子点分子的系统, 在量子点处于激发态, 量子点分子处于基态, 腔场A、B均处于真空态的初始条件及共振相互作用情况下, 探究了量子点、量子点分子与腔场之间以及两腔场之间的纠缠动力学特性.结果表明, 子系统之间纠缠发生不规则振荡.随着腔场耦合的增强, 量子点与量子点分子间纠缠增强, 量子点分子与腔场B间的纠缠、量子点与腔场A间及腔场A与B间的纠缠都减弱;无论在腔场弱耦合或强耦合下, 随着量子点分子隧穿程度的增加, 上述子系统之间的纠缠仅有量子点分子与腔场B间的纠缠度有明显减弱.
| [1] |
Vahala K. Optical microcavities[J].
Nature, 2003, 224: 839-846.
|
| [2] |
Raimond J, Brune M, Haroche S. Manipulating quantum entanglement with atoms and photons in a cavity[J].
Rev Mod Phys, 2001, 73(3): 565-580.
DOI: 10.1103/RevModPhys.73.565. |
| [3] |
Cho J, Angelakis D G, Bose S. Heralded generation of entanglement with coupled cavities[J].
Phys Rev A, 2008, 78(2): 022323.
DOI: 10.1103/PhysRevA.78.022323. |
| [4] |
Fidio C D, Vogel W. Entanglement signature in the mode structure of a single photon[J].
Phys Rev A, 2009, 79(5): 050303.
DOI: 10.1103/PhysRevA.79.050303. |
| [5] |
Song J, Song X D, Xia Y, et al. Efficient creation of continuous-variable entanglement for two atomic ensembles in coupled cavities[J].
Phys Rev A, 2011, 83(5): 052309.
DOI: 10.1103/PhysRevA.83.052309. |
| [6] |
Shen L T, Yang Z B, Wu H Z, et al. Control of two-atom entanglement with two thermal fields in coupled cavities[J].
J Opt Soc Am B, 2012, 29(9): 2379-2385.
DOI: 10.1364/JOSAB.29.002379. |
| [7] |
Sivakumar S. Entanglement of fields in coupled cavities: Effects of pumping and fluctuations[J].
Phys Lett A, 2010, 374(15-16): 1793-1799.
DOI: 10.1016/j.physleta.2010.02.010. |
| [8] |
Li W Z, Zhang C L, Shen L T, et al. Entanglement dynamics and maitaenance for two atoms in coupled cavities[J].
Opt Commun, 2014, 315: 213-219.
DOI: 10.1016/j.optcom.2013.11.017. |
| [9] |
卢道明. 原子与耦合腔相互作用系统中的纠缠特性[J].
物理学报, 2011, 60(9): 090302.
Lu D M. Entanglement properties in the system of atoms interacting with coupled cavities[J]. Acta Phys Sin, 2011, 60(9): 090302. |
| [10] |
Ogden C D, Irish E K, Kim M S. Dynamics in a coupled-cavity arry[J].
Phys Rev A, 2008, 78(6): 063805.
DOI: 10.1103/PhysRevA.78.063805. |
| [11] |
Benyoucef M, Kiravittaya S, Mei Y F, et al. Strongly coupled semiconductor microcavities: A route to couple artificial atoms over micrometric distances[J].
Phys Rev B, 2008, 77(3): 035108.
DOI: 10.1103/PhysRevB.77.035108. |
| [12] |
周青春, 周昱. 隧穿量子点分子Jaynes-cummings模型的Berry相位[J].
广东工业大学学报, 2013, 30(2): 18-22.
Zhou Q C, Zhou Y. Berry phase in Jaynes-cummings model for a tunneling quantum-dot molecule[J]. Journal of Guangdong University of Technology, 2013, 30(2): 18-22. |
| [13] |
周青春, 狄尊燕. 声子对隧穿量子点分子辐射场系统量子相位的影响[J].
物理学报, 2013, 62(13): 134206.
Zhou Q C, Di Z T. Phonon effect on the quantum phase of a radiation field interacting with a tunneling-coupled quantum-dot molecule[J]. Acta Phys Sin, 2013, 62(13): 134206. DOI: 10.7498/aps.62.134206. |
| [14] |
Cheng M T, Ma X S, Luo Y Q, et al. Entanglement generation and quantum state transfer between two quantum dot molecules mediated by quantum bus of plasmonic circuits[J].
Appl Phys Lett, 2011, 99(22): 223509.
DOI: 10.1063/1.3664637. |
| [15] |
Li J, Yu R, Huang P, et al. Carrier-envelope phase-dependent electron tunneling in a coupled double-quantum-dot system driven by a few-cycle laser pulse[J].
Phys Lett A, 2009, 373(21): 1896-1900.
DOI: 10.1016/j.physleta.2009.03.053. |
| [16] |
Li J H, Yu R, Ding C L, et al. Tunneling-induced π-phase shift of a quantum-dot molecule coupled to a single-sided cavity[J].
Eur Phys J D, 2011, 62(3): 425-431.
DOI: 10.1140/epjd/e2011-10649-7. |
| [17] |
Villas-Boas J M, Govorov A O, Ulloa S E. Coherent control of tunneling in a quantum dot molecule[J].
Phys Rev B, 2004, 69(12): 125342.
DOI: 10.1103/PhysRevB.69.125342. |
| [18] |
Vidal G, Werner R F. Computable measure of entanglement[J].
Phys Rev A, 2002, 65(3): 032314.
DOI: 10.1103/PhysRevA.65.032314. |
 2014, Vol. 31
2014, Vol. 31