在结构非线性分析中,学者们对恢复力模型进行了大量的研究,目前恢复力模型按照曲线形式可分为曲线型和折线型[1].曲线型恢复力模型所表现的刚度与工程实际较为接近,但在非线性地震响应计算中利用该模型有着诸多的不便,如计算量大、迭代次数多等;折线型恢复力模型通过对实验数据的抽象和简化,得到较为简单实用的数值模型,此类模型有一个重要的特点就是存在人为的拐点,即刚度突变点[2].若在计算过程忽略这些拐点的处理,可能会造成计算结果的失真,拐点的处理也是研究中的一项重要工作.本文以单自由度体系拐点处理方法为基础,引入多自由度体系的拐点处理流程,其主要目的是研究拐点处理对结构地震响应的各个精度指标的影响,分析结果可供折线型恢复力模型的地震响应相关研究参考.
1 恢复力模型的拐点[3-6]笔者以一个常用的三线退化模型为例来阐述恢复力模型拐点的概念, 如图 1所示.
|
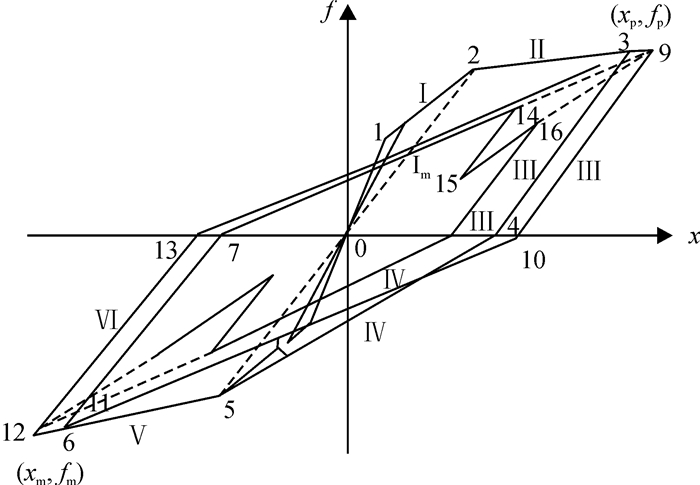
图 1 三线型恢复力模型 Figure 1 Three-line model of restoring force |
从图 1中可以看到标有数字的点都为模型的拐点,拐点前后恢复力曲线切线刚度显著变化,甚至出现正负号改变情况,所以说拐点就是恢复力模型两个不同刚度状态改变的临界点.
有如下几类拐点:第1类拐点,由弹性阶段0进入弹塑性Ⅰ或由弹塑性Ⅰ进入塑性Ⅱ的拐点,如图 1的1、2点,此类拐点的特点是刚度由大变小,切线刚度符号不变; 第2类拐点,由处于弹塑性阶段Ⅱ进入弹性卸载阶段Ⅲ的分界点,如图中的3、14点等,拐点前后切线刚度符号相反; 第3类拐点,此类拐点是进入弹塑性阶段之后卸载至平衡位置,而进入反向加载阶段的分界点,如图 1中x轴上的点4、7、10、13等.
2 拐点处理的方法迄今为止,学者们已经提出了许多种拐点处理方法,目前最常见的方法是以拐点为分界点,在逐步积分过程中改变时间步长以保证每个时间步长内结构或者构件的刚度无变化[7-9].其具体做法是将包含拐点的时间步长Δt一分为二,形成两个小步长Δt′和(Δt-Δt′),再重复一次积分.逐步积分时,首先按时间步长Δt′采用刚度K1进行计算,再按步长(Δt-Δt′)采用刚度K2进行积分计算.通过拐点以后的计算采用正常步长Δt的积分形式,刚度用改变后的K2进行积分.所以处理拐点的关键是确定Δt′,常用的确定方法有下列二分法和线性插值法.
2.1 二分法二分法作为试算法中最简单的一种,通过每次把函数f(x)的零点所在的区间收缩一半的方法,使区间的两个端点逐步迫近函数的零点,以求得零点的近似值.利用这种方法可以比较简单地求得拐点所处的时刻.下面以第一相限内的拐点为例,说明Δt′的确定方法.
对于第1和第2类拐点,设定弹塑性分界点临界力为Fs,如果在t时刻层间剪力为Ft<Fs,t+Δt时刻Ft+Δt>Fs,在此时步内必然有一点使Ft+Δt′=Fs.在处理模块中开始令Δt′=Δt/2,计算得Ft+Δt′与Fs进行比较.若Ft+Δt′<Fs则说明Δt′∈(Δt/2, Δt),取Δt′=Δt/2+(Δt/2)/2继续试算;若Ft+Δt′>Fs则说明Δt′∈(0, Δt/2),取Δt′=Δt/2-(Δt/2)/2继续迭代试算,直至精度达到要求使Ft+Δt′=Fs此点就为拐点.将此时步一分为二,Δt′和(Δt-Δt′)进行逐步积分,完成拐点处理.对于第3类拐点,即平衡位置的拐点,此类拐点处理方法与第1类相类似,令Fs=0即可.
2.2 线性插值法线性外插法是数值分析的方法结合结构的运动规律,可以一次就确定Δt′,由分段线性化假定可以推出下列3种拐点处理方法[10-13].
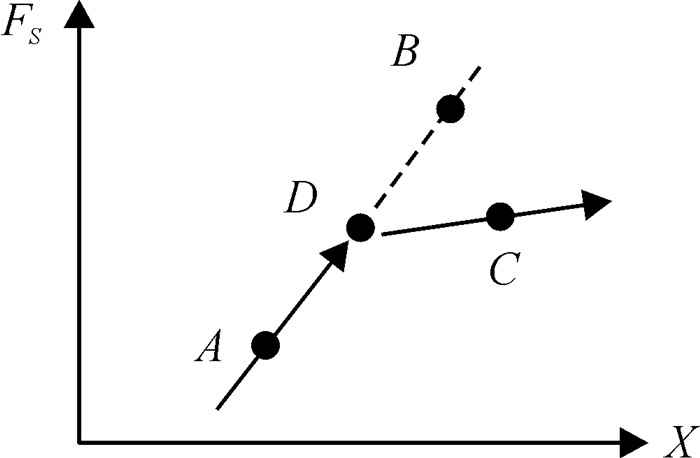
第1类拐点处理,如图 2所示,结构从弹性阶段进入弹塑性阶段.假设t时刻系统处在A点,在t+Δt时刻后计算值跨越D点直接到达B点,而实际情况应该是在C点.由线性关系假定有
| $ \Delta t' = \frac{{{F_D} - {F_t}}}{{{F_{t + \Delta t}} - {F_t}}}\Delta t. $ |
|
图 2 第1类拐点示意图 Figure 2 First type of inflection point |
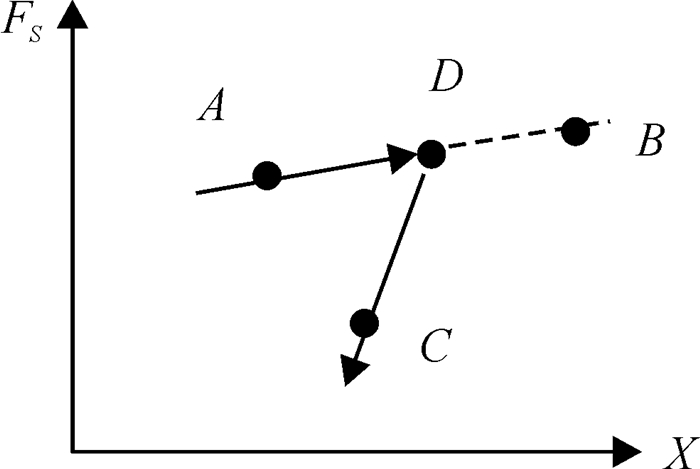
第2类拐点的处理, 如图 3所示,设t时刻系统处于A点,在下一时步进入卸载阶段,t+Δt时刻计算之后直接越过D点至B点,实际应该到达C点.在这种情况下,利用D点的速度ẋD=0这个条件可得:
| $ \Delta t' = - \frac{{2{{\dot x}_A}}}{{{{\dot x}_A} + {{\dot x}_B}}}. $ |
|
图 3 第2类拐点示意图 Figure 3 Second type of inflection point |
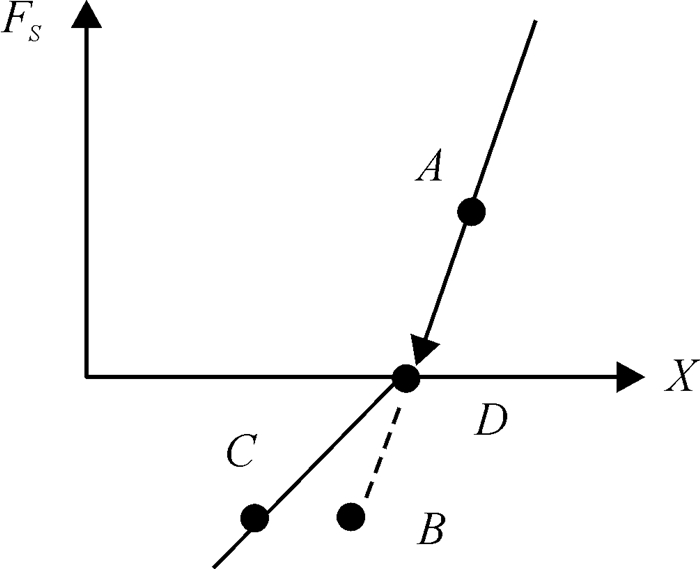
第3类拐点的处理, 如图 4所示.当结构在t时刻到达A点,t+Δt时刻计算值后到达反向加载阶段B,实际应该在D点到达平衡位置,再由D点到达C点,此时根据D点恢复力PD=0这一条件可得
| $ \frac{{{P_A}}}{{{P_B}}} = \frac{{\Delta t'}}{{\Delta t{\rm{ - }}\Delta t'}} \Rightarrow \Delta t'{\rm{ = }}\frac{{{P_A}}}{{{P_A} + {P_B}}}\Delta t. $ |
|
图 4 第3类拐点示意图 Figure 4 Third type of inflection point |
由以上方法得到的Δt′,令
由平均常加速度假设可以确定D点的地震加速度ẋg, t+Δt′,
| $ {{\dot x}_{g, t + \Delta t'}} = {{\dot x}_{g, t}} + \rho \left( {{{\dot x}_{g, t + \Delta t}} - {{\dot x}_{g, t}}} \right). $ |
由此返回A点重新进行时步为Δt′和(Δt-Δt′)的逐步积分计算.
3 多自由度体系的拐点处理在多自由度体系进行弹塑性时程分析与单自由度的计算相比具有一个很大不同点,就是在某一时步可能同时有多个自由度经历拐点[14-15],这些自由度进入状态改变时刻则是根据具体情况而定的,并且这些自由度之间状态改变具有耦合的影响关系.因此,前面所述的单自由度处理方法必须经过处理才能应用到多自由度体系的拐点处理中.
对多自由度体系的拐点处理,笔者在单自由度体系处理方法的基础上引入状态判定模块进行处理.其处理方法的机理是将步长Δt根据各自由度改变状态的先后时刻进行切分,保证每一被切分时步内的结构刚度无改变.
下面以i个自由度的结构体系,用Newmark增量形式的逐步积分方法来处理拐点为例,说明Δt′(i)的确定过程.
当多个自由度在同一时步进入弹塑性阶段时,记录这些层的恢复力F(i)和位移x(i),由2.2所提到的方法可以得到各个状态改变的自由度的Δt′(i),将得到的Δt′(i)数据进行由小到大的排序,取其中Δt′(i)最小值作为积分时步重新进行积分计算,计算完成之后对应结构刚度Ki随之改变.完成一次调整之后,对余下的自由度按上述步骤进行检查,直至所有刚度状态调整的自由度都得到处理.将时间(Δt-Δt′)再进行一次积分,完成此时步的处理,进入下一时步积分.
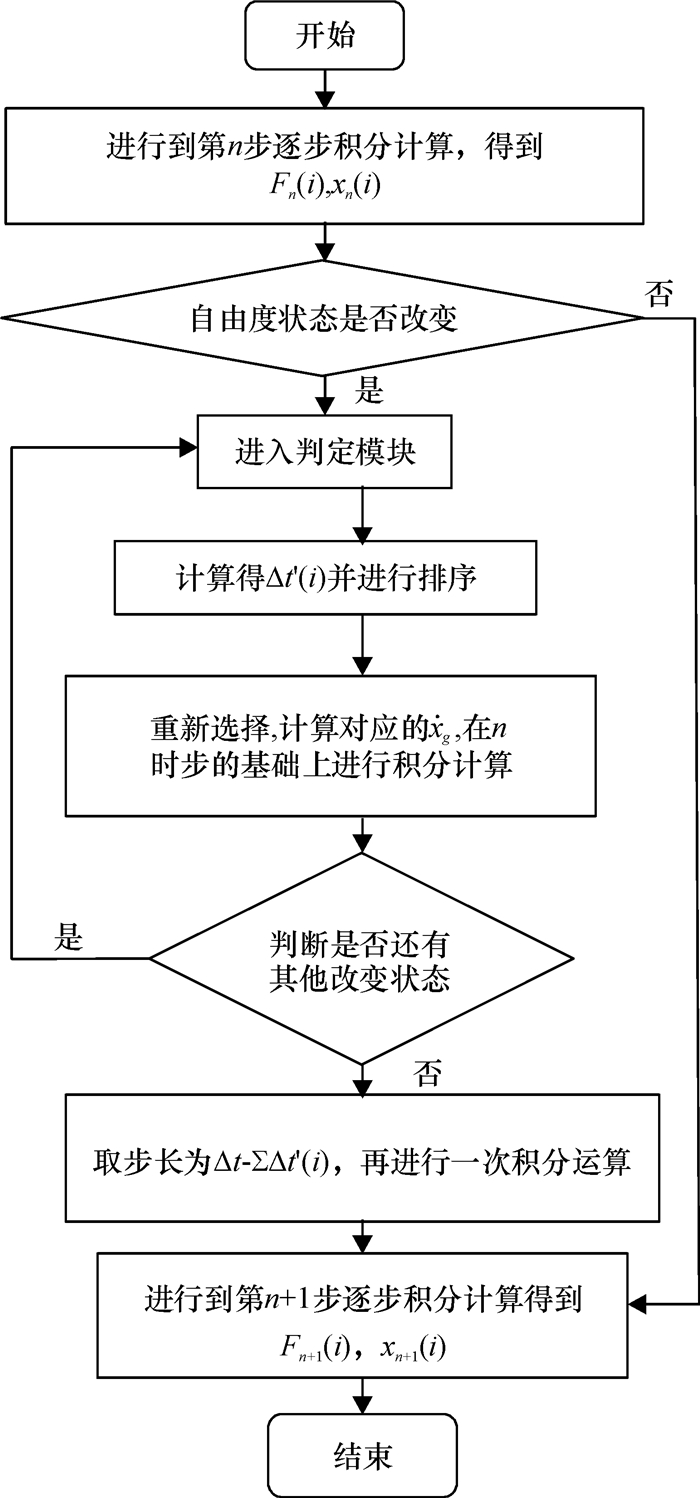
为了清晰地说明对多自由度体系的拐点处理,笔者利用程序设计流程图的方式进行说明,如图 5所示.
|
图 5 多自由度体系拐点处理流程图 Figure 5 Flow chart of inflection point processing in the MDOF system |
某学生宿舍,结构基本信息如表 1所示,结构为6层混凝土框架结构,柱截面为500 mm×500 mm,层高为3 m.结构数据如下,K为抗侧刚度,M为质量.
| 表 1 结构基本信息 Table 1 The information on the structure |
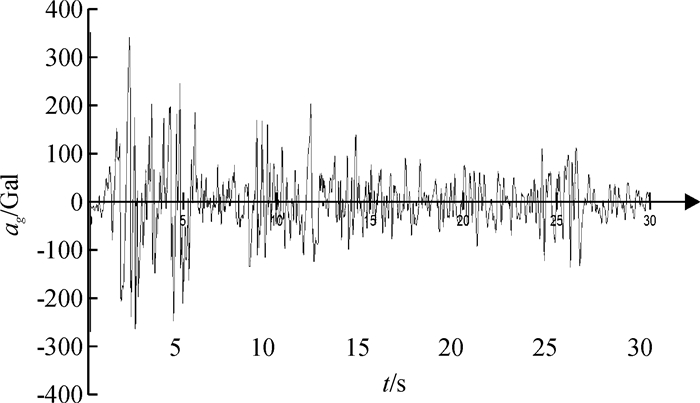
结构进行地震弹塑性时程分析计算时ẋg采用El_centro波,在8度罕遇地震(400 gal)的作用下,结构恢复力模型采用理想弹塑性Clough恢复力模型,结构阻尼采用瑞利阻尼,各层进入弹塑性阶段时的屈服剪力如表 2及图 6所示.
|
图 6 El_centro地震波 Figure 6 El_centro seismogram |
| 表 2 恢复力模型信息 Table 2 Information on the force restoring model |
将以上数据代入运动方程
| $ \left[ M \right]\left\{ {\dot x} \right\} + \left[ C \right]\left\{ {\dot x} \right\} + \left[ K \right]\left\{ x \right\} = \left[ M \right]\left[ I \right]{{\dot x}_g}. $ |
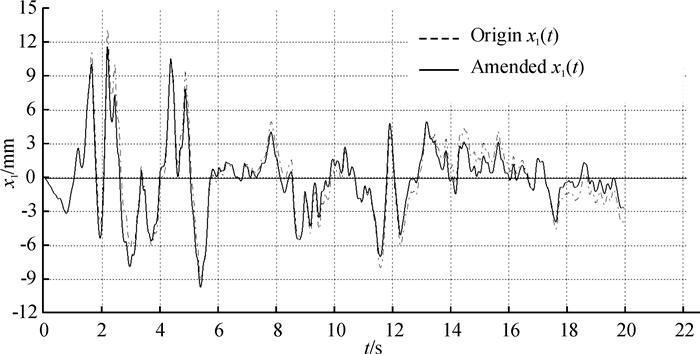
采用Newmark-β积分方法进行逐步积分,编制相关的Visual Basic计算程序进行计算,得到的底层位移时程曲线结果对比(虚线部分表示拐点不进行处理的结果),如图 7所示.
|
图 7 底层层间位移时程响应曲线对比(20 s) Figure 7 Comparison of the time history response curve of displacement for first layer (20 s) |
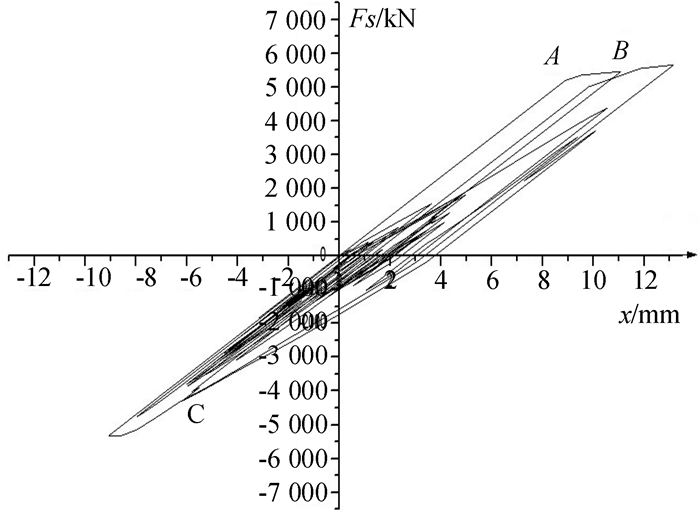
第1类拐点的影响,对比图 8与图 9,图中A点为结构第一次经历第1类拐点,未调整之前的幅值x1(t)为9.04 mm,调整之后的幅值x′1(t)为8.75 mm.由此可知第1类拐点不进行处理,位移幅值结果是偏大.
|
图 8 底层层间剪力滞回曲线(未调整) Figure 8 Hysteresis curve of interlayer shear force at first layer (Origin) |
|
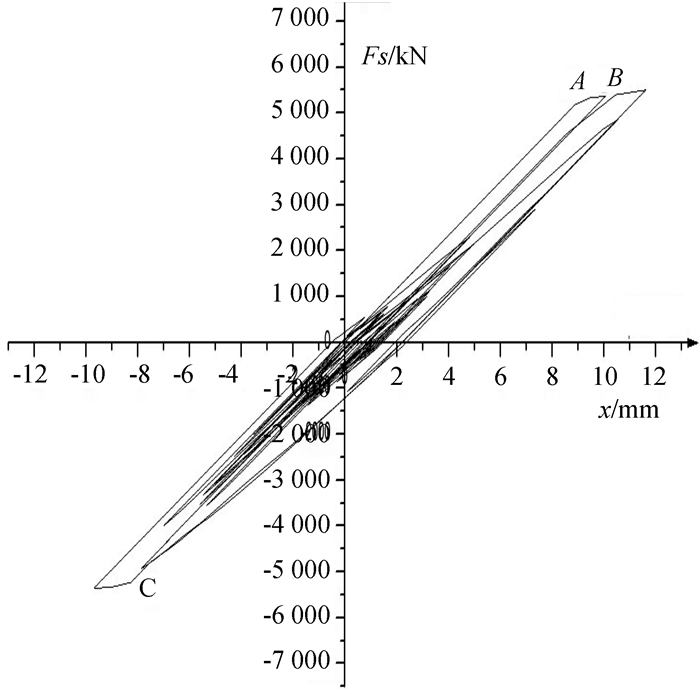
图 9 底层层间滞回曲线(调整后) Figure 9 Hysteresis curve of interlayer shear force at first layer (Amended) |
第2类拐点的影响,由图 7中可得结构在1.72s经历了第2拐点,即极大值点,该点为结构第一次进入弹塑性之后的卸载点,对比图 8与图 9中B点值,未做拐点处理x1(t)为10.30 mm,调整之后的幅值x′1(t)为9.56 mm,考虑到第1类拐点的累计偏差0.29 mm,此点的偏差仍然达到0.45 mm,所以说第2类拐点不做处理,结构位移计算幅值也是偏大.
第3类拐点处理与否的对位移幅值的结果影响,在图 8与图 9中由于在平衡点位置滞回曲线过密难以进行分析,但由图 7结果可得,在1.84 s,3.02 s时均为进入反向弹塑性阶段,但此时调整后的x′1(t)值明显大于x1(t)值,这说明该类拐点不做处理会使结构位移计算幅值偏小,与前面两种拐点的影响情况正好相反.
由于以上各种偏差的累积效应,随着时间的推移结构的位移时程曲线分离现象越来越明显.
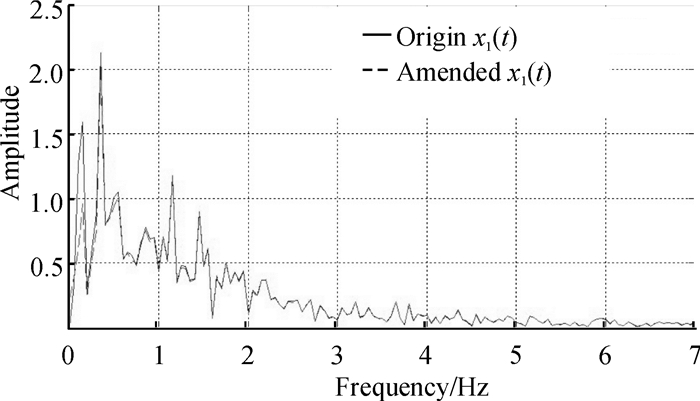
4.2.2 拐点处理对结构频率的影响将图 7得到的时程分析结果,用快速傅立叶变换函数处理后可得位移-频率响应谱,如图 10所示.由图 10层间位移响应谱可以得出,两条频谱曲线的差别主要集中在低频区的0.1~1 Hz之间,其中大约0.15 Hz处差别最大,相差达到32%,在1Hz以后区域两条曲线基本上是重合的,说明结构对较高频域拐点处理并不敏感.
|
图 10 层间位移-频率响应谱 Figure 10 Spectrum of interlayer amplitude-frequency |
由图 7可知,拐点处理后的时程曲线与处理前的时程曲线的变动趋势相同,一直到20 s处结构的振动相位基本保持一致.这说明拐点处理只是调节刚度状态改变的时刻.在切分时步时,假定时步内的地震加速度为线性变化的,这是拐点处理对结构振动相位变化不大的主要原因.
5 结论本文基于折线型恢复力模型,介绍了模型拐点处理的概念及其处理方法的理论基础.从简易的程序迭代计算的二分法和利用力学性质进行分析的线性插值法出发,阐述单自由度体系的拐点处理方法.以单自由度的拐点处理方法为基础推导得到多自由度体系的处理流程,将其作为程序中的一个处理模块对多自由度的地震响应进行计算修正.
最后采用上述的处理流程对一个6层层模型的算例进行时程分析,并结合其结果对比可得,第一和第二类拐点处理对地震时程分析振幅的影响是使其结果偏小,而第三类拐点处理使振幅变大.通过位移频率响应谱的结果可知,拐点处理对结构的频率影响主要在低频阶段,本文主要集中在0.1~1 Hz之间.而在结构振动相位方面,拐点处理对此基本没有影响.
| [1] |
张新培.
钢筋混凝土结构抗震非线性分析[M]. 北京: 科学出版社, 2003: 68-72.
|
| [2] |
张雄, 王天舒.
计算动力学[M]. 北京: 清华大学出版社, 2011: 163-169.
|
| [3] |
李爱群, 丁幼亮.
工程结构抗震分析[M]. 北京: 高等教育出版社, 2010: 140-142.
|
| [4] |
徐赵东, 郭迎庆.
Matlab语言在建筑抗震工程中的应用[M]. 北京: 科学出版社, 2007: 143-177.
|
| [5] |
邱法维. 拟动力实验中的数值积分方法[J].
哈尔滨工业大学学报, 1994(3): 120-127.
Qiu F W. Numerral intergration of the pseudo-dynamic test[J]. Journal of Harbin Institute of Technology, 1994(3): 120-127. |
| [6] |
马恺泽, 梁文兴, 李响, 等. 型钢混凝土剪力墙恢复力模型研究[J].
工程力学, 2011(8): 119-125.
Ma K Z, Liang W X, Li X, et al. Steel reinforced concrete shear wall restoring force model research[J]. Engineering Mechanics, 2011(8): 119-125. |
| [7] |
霍瑞丽, 郭建. 中高层钢筋混凝土异形柱框架-抗震墙结构弹塑性时程分析[J].
地震工程与工程振动, 2001(3): 90-95.
Huo R L, Guo J. Elastic-Plastic dynamic analysis of RC frame-aseismic wall structure with special-shape columns[J]. Journal of earthquake engineering and engineering vibration, 2001(3): 90-95. |
| [8] |
Christopher Ariyaratana Larry A Fahnestock. Evaluation of buckling-restrained braced frame seismic performance considering reserve strength[J].
Computers & Structures, 2001, 33(1): 77-89.
|
| [9] |
肖明葵, 刘纲, 白绍良. 滞回恢复力模型中求折点的一种方法[J].
重庆大学学报:自然科学版, 2002, 25(1): 13-16.
Xiao M K, Liu G, Bai S L. A method of computing rigidity turning point in hysteretic restoring force models[J]. Journal of Chongqing University: Natural Science Edition, 2002, 25(1): 13-16. |
| [10] |
汪梦甫, 汪帜辉, 刘飞飞. 增量动力弹塑性分析方法的改进及其应用[J].
地震工程与工程振动, 2012(1): 30-35.
Wang M F, Wang Z H, Liu F F. Incremental dynamic elasto-plastic analysis method improvement and its application[J]. Journal of earthquake engineering and engineering vibration, 2012(1): 30-35. |
| [11] |
左淑红, 熊立红, 田志敏. 混凝土小砌块约束砌体结构的抗震性能——基于层间位移的分析[J].
世界地震工程, 2012, 28(2): 64-71.
Zuo S H, Xiong L H, Tian Z M. Seismic performance of concrete block-base on analysis of interlayer displacement[J]. World Earthquake Engineering, 2012, 28(2): 64-71. |
| [12] |
Pandey G R, Maki T. Seismic performance of bond controlled RC columns[J].
Engineering Structures, 2008, 30(9): 2538-2547.
DOI: 10.1016/j.engstruct.2008.02.001. |
| [13] |
齐鑫, 肖遥. 下辽河地区典型土层时域与频域方法对比[J].
世界地震工程, 2012, 32(1): 23-29.
Qi X, Xiao Y. Contrast of time domain and frequency domain methods for typical soil of Xialiao area[J]. World Earthquake Engineering, 2012, 32(1): 23-29. |
| [14] |
曹征良, 洪翔, 吴兵. 层间弯剪型高层结构的弹塑性地震反应分析[J].
深圳大学学报:理工版, 2004, 21(2): 16-22.
Cao Z L, Hong X, Wu B. Elastic-plastic earthquake response analysis of story-post shear-bending tall building structures[J]. Journal of Shenzhen University Science and Engineering:Natural Science Edition, 2004, 21(2): 16-22. |
| [15] |
朱伯龙, 张琨联.
建筑抗震设计原理[M]. 上海: 同济大学出版社, 2007.
|
 2014, Vol. 31
2014, Vol. 31